突出煤相似材料单轴压缩的PFC2D模型细观参数标定研究

冯康武

（1.中煤科工集团重庆研究院有限公司，重庆 400037；2.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037）

煤与瓦斯突出物理模拟试验是研究煤与瓦斯突出力学机理的有效手段，根据现场资料及统计分析得到，突出煤层普遍具有结构破坏性高、孔隙发达、比表面积庞大、抗压强度低等特点。目前在相似材料配比研究方面，国内外大量专家做过相关研究。例如张建国[1]等通过突出危险煤层煤样压制成型煤；康向涛[2]等选用煤粉作为骨料，石膏和水泥作为胶结剂制作相似材料模拟原煤，研究了型煤的强度及破坏特性，忽略了其他物理力学性质。而在模拟材料的细观参数标定方面的研究主要以各类岩石或者沙土为研究对象，刘畅[3]等针对白云质灰岩的单轴压缩和双轴压缩试验，采用实验方法，得出白云质灰岩在平行黏结模型中的细观参数与宏观特征的关系表；彭国园[4]等根据室内三轴试验获得的红黏土宏观力学性质指标，通过颗粒流数值三轴试验，标定出红黏土颗粒的接触力、接触模量、黏结强度等细观力学参数。由于试验条件的限制，目前针对煤与瓦斯突出试验力学机理的研究主要采用室内真三轴突出模拟试验平台，试验材料主要采用相似材料或者压制成型的型煤，但由于物理模拟试验实施过程复杂、准备工作较多，不利于多次重复试验，而数值试验恰恰满足了这方面的要求，目前针对数值试验所必须的相似材料的细观参数标定的研究鲜有报道，这也制约了采用颗粒流等数值方法对突出模拟试验的数值试验的开展，从试验相似材料内部细观上了解突出发生过程中内部裂纹扩展以及受力特征。基于此，主要从已有相似材料的宏观力学指标出发，采用迭代方法，对相似材料的细观参数进行标定，希望对后期煤与瓦斯突出力学机理研究过程中数值模拟试验的开展提供基础数据。

1 相似材料配比方法及宏观力学指标

1.1 相似材料配比方法

突出模拟相似材料的配比主要采用砂子、活性炭和粉煤作为骨料，水泥作为胶结材料，水作为辅料。按照一定比例进行配比[5]，其中水泥为425 号普通硅酸盐水泥，质量占比为10%～16%，砂子为普通干燥河砂，粒级为 40～20 目（380～830 μm），质量占比为 1%～7%，活性炭采用 2.5～5.6 mm 干燥颗粒，粉煤采用自然干燥的40～20 目粉煤，质量占比为70%～80%。

1.2 宏观力学参数指标

1）采用标准圆柱形试件进行室内物理力学试验，试件尺寸为高100 mm，截面直径50 mm 的圆柱形标准尺寸，试件加载保压压力为25 MPa，采用模具压制完成后放置于干燥皿中养护17～19 d 后进行标准件制作，根据相应的单轴压缩试验和巴西劈裂等室内试验，相似材料物理试验宏观力学参数见表1。按照数值试验模型尺寸与物理试验一致原则，后期试样高度H 取100 mm，宽度D 为50 mm，颗粒密度ρ 为 1.36 g/cm3，弹性模量取 44.5 MPa，泊松比 μ 取0.207，单轴抗压强度 σc取 0.67 MPa，抗拉强度 σt取0.014 MPa。

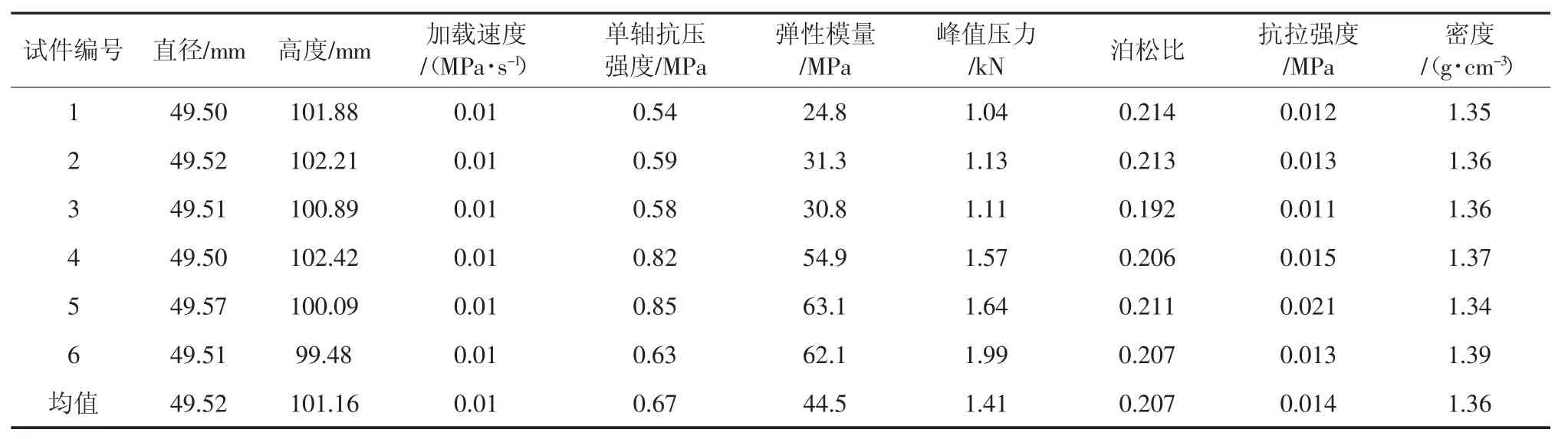
表1 相似材料物理试验宏观力学参数Table 1 Macro mechanical parameters of physical tests of similar materials

2）根据试样尺寸综合考虑，确定数值模型最小颗粒粒径为 0.6 mm，最大颗粒粒径为 0.99 mm（保证粒径比为1.66），为了保证相应的计算精度和减小边界效应，模型最短边颗粒数目应大于30 个，同时满足试件最短边颗粒数目大于30 个。

2 颗粒流基本理论

颗粒流数值模拟方法（PFC）属于离散单元法的一种，离散单元法是将散粒体分离成离散单元的集合，利用牛顿第二定律建立每个单元的运动方程，运用迭代法进行求解。二维颗粒流程序通过圆形离散单元来模拟颗粒介质的运动及其相互作用，并通过运动定律（牛顿第二定律）和变形定律（胡克定律）实现对材料变形特征的模拟。颗粒流程序提供了3 种基本的接触本构模型，分别是接触刚度模型、滑动模型和黏结模型。其中，接触刚度模型提供了接触力和相对位移的弹性关系；滑动模型则强调法向和切向接触力，使得接触颗粒可以发生相对移动；黏结模型是限制总的法向和切向力，使得颗粒在黏结强度范围内发生接触、黏结断裂等情况[6]。

根据突出模拟材料的配比方法，除砂子、活性炭等骨料以外，加入了水泥、水等胶结材料，而平行黏结模型可以很好的模拟颗粒之间一定尺度内存在的黏结材料的本构行为，颗粒间平行黏结示意图如图1，这些符合砂子、活性炭等骨料被水泥胶结包裹的组成特性，因此，在相互接触的颗粒间赋予平行黏结模型可以实现对突出模拟材料宏、细观受力特征的模拟。

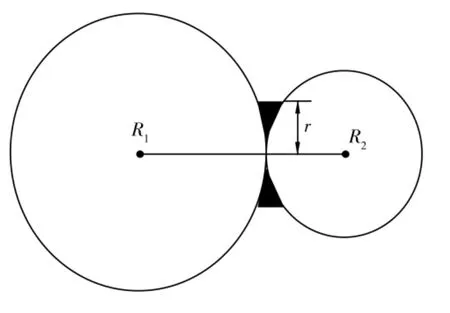
图1 颗粒间平行黏结示意图Fig.1 Sketch map of parallel adhesion between particles

3 细观参数标定方法

3.1 标定原则

细观参数的标定是根据前期宏细观参数之间的相关关系，通过建立数值模型，并初步赋予一定初值的细观力学参数，并对被赋予假定力学参数的颗粒数值试样模型进行数值试验，然后通过岩石数值试验与室内试验对比进行颗粒流细观参数标定，通过迭代方法不断调整细观力学参数，使得数值试验所得到的弹性模量、峰值强度、峰值破坏压力等宏观参数与室内试验所得到的宏观参数实现最大的匹配度。

3.2 标定步骤

目前常用试错迭代法标定细观参数，即通过对比数值试验和室内力学试验的结果，不断调整细观参数以达到两者基本匹配。根据单轴压缩数值试验的应力-应变曲线结合计算式（1）、式（2）可得到抗压强度、弹性模量E（此处弹性模量取工程上常用的50%抗压强度点的割线模量）和泊松比，根据巴西劈裂试验计算式（3）可以得到抗拉强度。

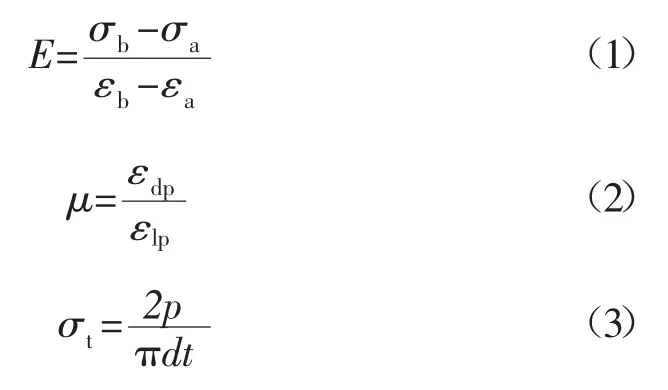
式中：σb、σa为应力应变曲线中直线段终点和始点的应力；εb、εa为应力应变曲线中直线段终点和始点的应变；μ 为试验试件的泊松比；εdp、εlp为应力应变曲线中对应直线段部分的横向应变、纵向应变的平均值；σt为试件中心的最大拉应力，即抗拉强度，MPa；p 为试验破坏时的极限压力，N；d、t 为承压圆盘的直径和厚度，mm。

细观参数标定流程共分为5 个步骤：

1）第1 步。选定最小颗粒半径Rmin，综合考虑模拟精度和计算效率的情况下，选择最小颗粒半径为0.6 mm，颗粒半径比为 1.66。

2）第2 步。调整接触等效弹性模量，等效弹性模量与宏观弹性模量正相关，在其他参数不变的情况下，满足宏观弹性模量。

3）第3 步。调整接触刚度比，接触刚度比与宏观参数泊松比μ 正相关，在已调整参数及其他参数不变的情况下，满足宏观参数泊松比μ。

4）第4 步。调整黏结法向强度，黏结内结法向强度与宏观参数峰值抗压强度正相关，调整黏结法向强度满足宏观峰值抗压强度。

5）第5 步。调整黏结切向强度，黏聚力、黏结法向强度同时与宏观参数峰值抗拉强度正相关，调整黏结内聚力满足宏观峰值抗拉强度。

3.3 平行黏结本构模型所需参数

在颗粒流的计算循环过程中，颗粒间的作用力主要遵循牛顿第二定律与力-位移定律，而颗粒的接触本构模型包含刚度模型、滑动模型和黏结模型3 个部分，由于研究对象为煤与瓦斯突出试验所用的相似材料，性质介于脆性材料与胶结材料之间，以平行黏结模型更能准确反映其宏细观力学性质。平行黏结模型细观参数主要包括接触细观参数和黏结细观参数，PFC2D模型的主要宏细观参数如下：

2）接触细观参数。①最大颗粒半径Rmax；②接触弹性模量E*；③接触刚度比kn/ks；④接触摩擦系数f;⑤法向/切向接触阻尼 βn/βs。

3）宏观参数。①单轴抗压强度σc；②弹性模量E；③泊松比 μ；④抗拉强度 σt。

3.4 数值试验过程

为了对比数值试验和室内力学试验的结果，需要分别进行模拟材料的单轴压缩数值试验和直接拉伸数值试验，单轴压缩数值试验模型如图2，巴西劈裂试验模型如图3。通过单轴压缩数值试验，根据试验应力-应变曲线可分别得到单轴抗压强度、弹性模量和泊松比，通过直接拉伸数值试验，根据试验破裂时的峰值强度可得到单轴抗拉强度。通过与物理试验结果的对比，可实现细观参数的标定。

图2 单轴压缩数值试验模型Fig.2 Numerical test model of uniaxial compression

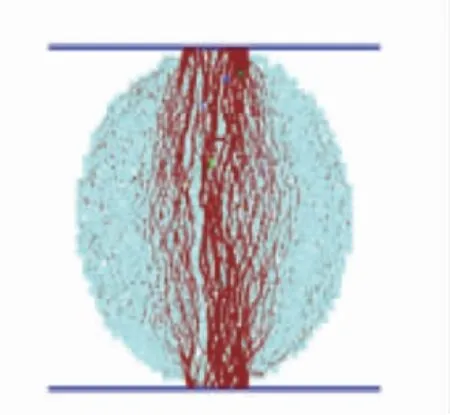
图3 巴西劈裂试验模型Fig.3 Brazilian split test model

根据相关研究[7]，材料单轴抗压强度与黏结强度有关。因此，首先将除黏结强度外的其余细观参数设为固定值：接触弹性模量与黏结弹性模量均取3.45×108Pa，即接触刚度比与黏结刚度比均取 2.0，即接触摩擦系数 f 为 0.5，黏结黏聚力=5×105Pa，黏结内摩擦角为0.47。进行一系列单轴压缩试验，得到黏结强度与材料单轴压缩强度的关系：

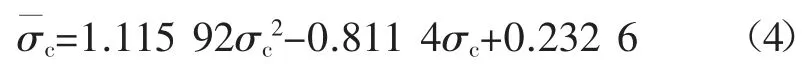
根据物理试验结果，模拟材料的单轴压缩强度为 0.67 MPa，得到黏结强度为 0.19 MPa，通过同样的处理方式，黏结弹性模量与宏观弹性模量正相关,得到黏结弹性模量与宏观弹性模量的关系:

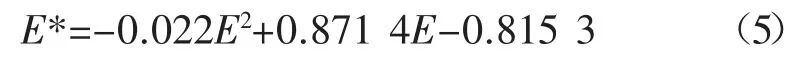
根据物理试验结果，模拟材料的弹性模量为44.5 MPa，得到黏结弹性模量 E* 为 26.3 MPa，泊松比与刚度比正相关，并结合刚度比的取值范围，可取刚度比为2.0，颗粒离散元中，黏结破坏后颗粒开始滑移，颗粒间的摩擦系数f 只影响材料达到应力峰值后的峰后力学行为，峰后的力学响应难以定量描述，根据相关研究[7]，岩石类材料摩擦系数取值范围为 0.25～0.75，初始值取为 0.47。

将上述参数建立细观模型，模型高100 mm，宽度为50 mm，含颗粒2 300 个，分别进行单轴压缩试验和巴西劈裂试验，并通过“五步法”分别对接触等效弹性模量、接触刚度比、黏结法向强度以及黏聚力进行调整，细观参数标定值和宏观参数结果见表2，数值试验与室内试验应力应变曲线对比如图4。单轴压缩室内试验与数值试验岩样破坏形态如图5。

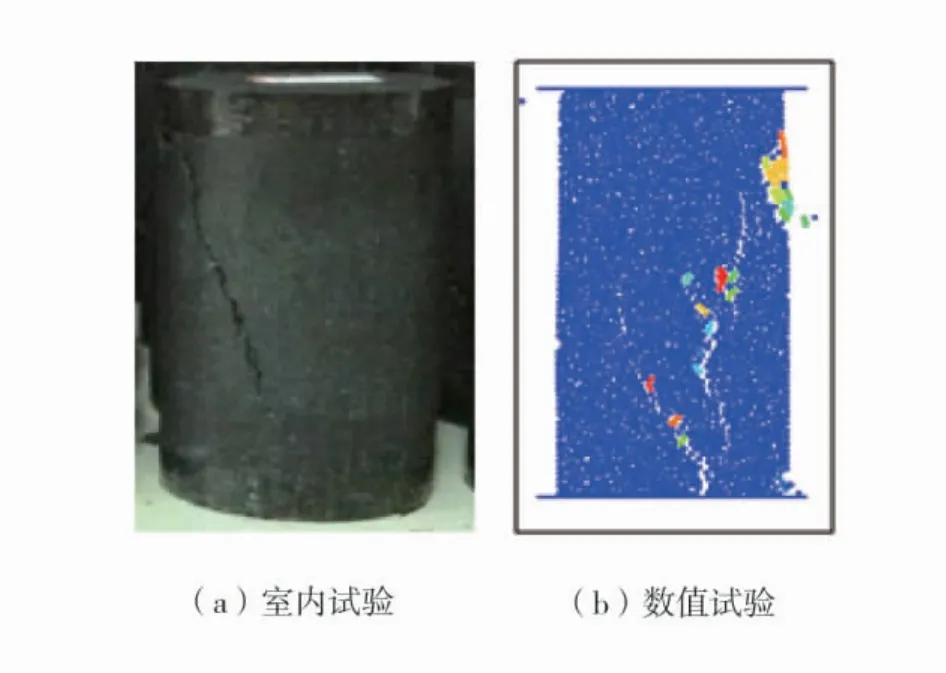
图5 单轴压缩室内试验与数值试验岩样破坏形态Fig.5 Failure modes of rock samples in laboratory and numerical tests under uniaxial compression

经过上述细观参数的调整，得到宏观参数抗压强度、弹性模量、泊松比和抗拉强度与物理试验宏观参数目标值的最大误差分别为1.49%、1.12%、3.86%和7.14%，相应的误差认为可以接受[8-10]，细观参数标定结束。

4 结 论

1）研究结果表明，利用离散元颗粒流程序建立的数值模型能够模拟突出相似材料单轴压缩试验和巴西劈裂试验的实际情况，通过不断调整细观力学参数进行重复数值试验，所得出的轴向应力应变曲线非常接近，通过细观参数计算得到的宏观抗压强度、弹性模量等误差较小。

2）通过对比数值试验与室内物理试验试件的破坏形态，均出现了1 条与轴向成30°左右夹角的贯通型裂缝，试件最终破坏是由于内部张拉裂纹、剪切裂纹逐步增加贯通导致的劈裂破坏，试件细观结构与其宏观本构行为之间联系紧密。

3）根据标定出的细观参数对模拟材料进行力学特性仿真试验，一方面具有低成本、可重复性强、试验条件理想等优点，同时满足在此基础上开展相应的突出模拟材料渗流、动力学试验的条件，为后期煤与瓦斯突出动力灾害试验提供了另外一种安全、可靠的理论分析手段。