基于SCSO-GRU模型的网络流量预测

高佰宏,刘朝晖,刘 华

(1.南华大学计算机学院,湖南 衡阳 421000; 2.南华大学电气工程学院,湖南 衡阳 421000)

0 引 言

随着通信技术的发展，网络规模和吞吐量急剧扩大，网络结构日益复杂，网络性能和服务质量问题日益突出，这给网络安全防御、网络故障修复以及网络资源分配规划的工作带来巨大的挑战。因此，准确地预测网络流量，掌握网络流量的变化规律，对网络安全态势变化趋向的把握，降低网络拥塞中的信息丢失和延迟，以及充分利用网络资源和提高服务质量，具有重要的意义[1]

网络流量预测主要根据流量的统计特征以及它们在时间序列值之间呈现出强相关性的特点进行预测。根据应用场合不同，网络流量预测一般又可分为短期预测、中期预测及长期预测[2]，相对中长期预测，短期预测更具挑战和研究价值[3]。

网络流量预测一直是网络领域的经典问题，过去提出了许多网络流量预测的方法，这些预测方法按流量时序特征的平稳性划分成线性预测(平稳)方法和非线性预测(非平稳)方法。传统线性预测模型主要有自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)、自回归合成移动平均模型(ARIMA)及差分自回归求和滑动平均模型[4]。这些线性模型针对小规模的稀疏网络流量预测具有很好的效果，但是，随着网络的复杂化和动态化，网络流量特性已偏离了相关学者早期认为的线性模型如高斯分布、泊松分布等[5]，以上传统的线性预测模型已经不能描述日益复杂的非线性的网络业务。

网络流量预测模型在较长时间内具有明显的非线性、多重分形性和突发性等特点，很多可以刻画上述特性的非线性模型被不断提出，现主要有灰色理论模型(Grey Theory, GT)、支持向量机(SVM)模型、混沌理论模型，以及人工神经网络(ANN)模型等。其中GT模型所需样本少，预测精度高，但是缺乏并行计算能力，且系统稍微变化可能导致计算结果出现较大的误差[6]；SVM很好地解决了小样本的学习问题，具有很好的泛化能力，但是由于缺乏结构化的方法确定模型中的一些关键参数，对模型的确定会产生一定影响[7]；混沌理论模型主要用于分析网络流量的自相似特性，主要分为全局法和局域法，全局法目前还在理论层面，局域法计算量小且对实际变化有很强的适应能力，但在计算方面要用到较多的存储空间，另外在求解模型参数和持续构造临近状态向量的过程中还需花很多的计算时间[4]；ANN模型有着自学习、自组织、并行计算能力强、容错性强等优点，可以很好地描述非线性特性，虽然存在着调参问题，但是，相比其他模型而言，有很大优势。近几年来，ANN模型已在网络流量领域引起了广泛关注和应用，常见ANN模型主要包括堆叠式自编码器(Stacked Auto-Encoder, SAE)、反向传播(Back Propagation, BP)神经网络、深度置信网络(Deep Belief Networks, DBN)、卷积神经网络(Convolutional Neural Network, CNN)以及循环神经网络(Recurrent Neural Network, RNN)等[8]。

RNN是一种引入了循环反馈机制的深层神经网络，能够考虑数据间的时序相关性，在学习具有长期依赖的时序数据上表现出更强的实用性[9]。长短期记忆(Long Short-Term Memory, LSTM)循环神经网络是RNN的一种特殊模型，由于其能够处理时间序列之间的长短期依赖关系，有效地解决了常规RNN训练过程中的梯度消失和梯度爆炸问题，现已有不少文献将LSTM模型应用到网络流量预测中，该模型已成为主流的网络流量预测模型之一[10-11]。但是，LSTM模型被应用到大规模网络中时，计算成本相当大，这在具有严格等待时间要求的任务中是不能容忍的，对网络流量进行实时精确的预测仍存在一定的挑战[12]。门控循环单元(Gated Recurrent Unit, GRU)是LSTM的一种简化，在保证预测精度的同时，具有结构简单、参数少、训练时间少等优点[13]。

与LSTM循环神经网络一样，GRU循环神经网络在进行网络参数确定时采用的是反向误差传播(Back Propagation Through Time, BPTT)算法，该算法复杂度非常高，并且容易收敛于局部最优解。

基于正余弦的群优化(SCSO)算法[14]是一种新型的元启发式算法，它是基于正余弦算法改进的自组织和群智能的数值优化算法。首先，该算法在搜索空间中随机生成一定个体维度和种群规模的粒子群；然后，通过目标函数计算每一维度内的每个粒子个体适应度值，通过比较得到粒子最优值pbest，并且更新基于正余弦的粒子更新方程；最后，比较个体最优值找出全体最优值。该算法的优势在于结构简单、参数少且非常易于实现[15-16]。为解决网络流量预测中GRU模型参数优化问题，本文在GRU模型中引入了SCSO算法，提出一种SCSO-GRU模型。该模型通过SCSO算法确定模型的最优参数，提高模型的预测准确率和训练速度。本文采用The UCI Network Data Repository真实数据集来验证SCSO-GRU模型的预测性能，并与LSTM和GRU模型进行比较。结果表明SCSO-GRU模型不管在预测精度方面还是收敛速度方面都优于LSTM和GRU模型。

1 GRU神经网络模型

传统的RNN网络，由于存在梯度消失现象，所以在实际中很难解决长期依赖问题，使得训练RNN变得相当困难[17]。为了解决这个问题，LSTM和GRU在隐藏层中引入了“记忆细胞”结构，使用不同的函数计算隐藏层的状态。LSTM的“记忆细胞”由输入门、遗忘门和输出门3个门构成，而GRU“记忆细胞”只由更新门和复位门组成，其训练参数更少。文献[18-19]验证了GRU在减少参数个数的同时，性能比LSTM更优。

GRU单元的数据流及操作如图1所示，更新门zt定义了上一时间步记忆保存到当前时间步的量，当取值越大时，表示当前神经元要保留的信息越多，而上一个神经元要保留的信息越少；复位门rt决定了如何将新的输入信息与上一时间步的记忆相结合，当式(2)取值为0时，表示要抛弃神经元传来的信息，即只要当前神经元的输入作为输入，这样就可以使当前的神经元抛弃一些上一时间步神经元的无用信息。

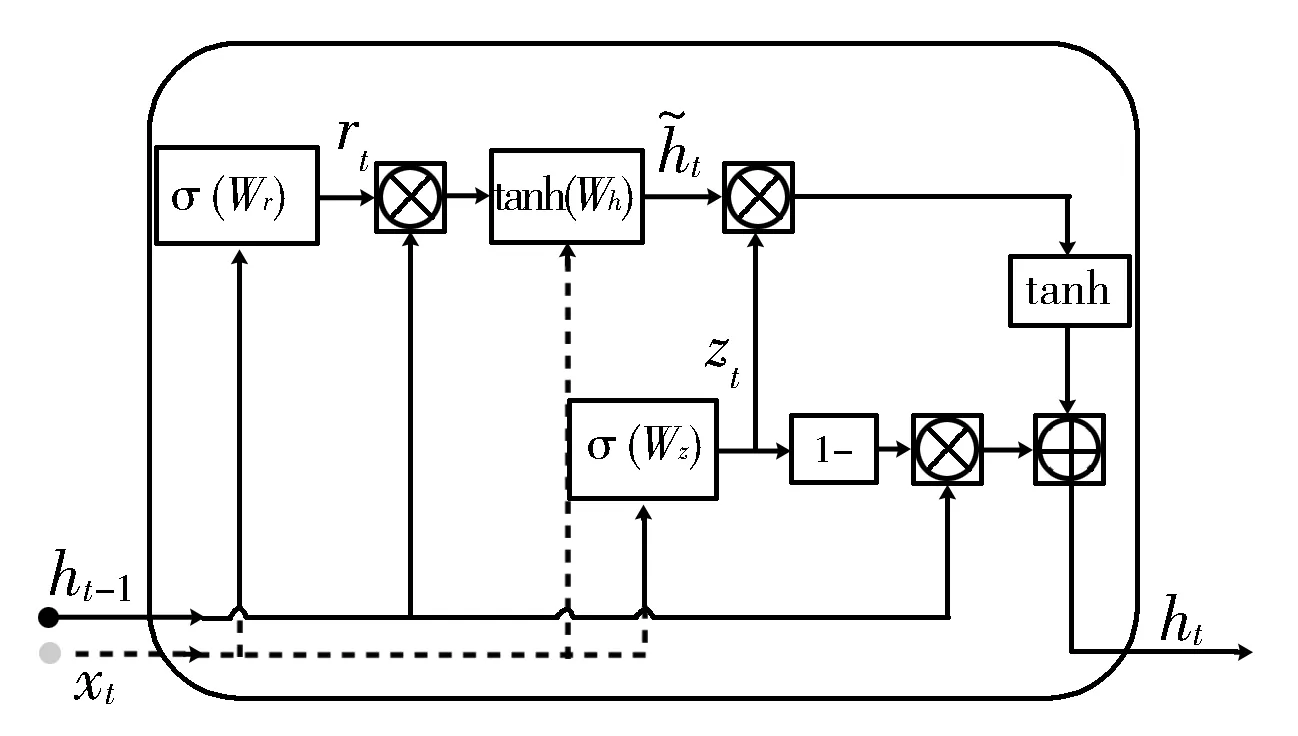
图1 GRU“记忆细胞”结构

GRU模型具体的计算公式如下：

zt=σ(Wz[ht-1,xt]+bz)

(1)

rt=σ(Wr[ht-1,xt]+br)

(2)

(3)

(4)

yt=σ(Wyht)

(5)

GRU神经网络的训练采用BPTT算法，其原理和BP算法原理类似，只是多考虑了误差项沿时间的反向传递。BPTT算法中目标函数的最优解是通过梯度下降(Gradient Descent, GD)算法得到的。在训练过程中，误差项将向上一个状态逐层传递，几乎不存在衰减。很长时间之前的状态和结尾状态都会影响各层权重的调整，最终训练出来的模型就具有较长时间范围内的记忆功能。然而，BPTT中的GD算法对优化函数和约束条件具有严格的连续性和可导性要求，在复杂的优化环境中计算复杂度高，收敛速度较慢且可能收敛于局部最优值[8]。

2 基于正余弦的群优化SCSO算法

近年来出现的群体优化算法很多，鉴于SCA算法容易实现、可调节参数少，以及具有相当快的逼近全局最优解的速度，该算法目前已被成功应用于函数优化和系统参数优化，并且在实际应用方面，正余弦算法很好地解决了优化飞机机翼翼型设计[20]这一具有挑战性的问题。考虑到SCA算法的上述优点，本文引入改进的SCA算法(SCSO算法)，以此来提高GRU神经网络模型的预测精度，降低计算复杂度，提高效率，通过找到最佳粒子实现对预测模型参数的优化。

2.1 SCA算法

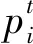
(6)

在每次迭代中，第i个个体的位置按式(7)的更新方程进行更新：

(7)

2.2 SCSO算法

(8)

(9)

与SCA算法一样，SCSO算法由初始值生成、局部最优选择、粒子更新和最优值选择组成。首先，在搜索空间中随机生成粒子。然后，通过目标函数计算个体最优值pbest，并且更新基于正余弦的粒子更新方程。在SCSO算法中，gbest粒子用于搜索全局最优。性能方面，SCSO算法与SCA算法及其他群优化算法相比，具有更高的最小化能力，并在数值函数优化方面取得了成功[14]。该算法步骤如下：

Step1在搜索空间中随机生成初始粒子：

Step2使用目标函数评估每个粒子，并计算个体最优值pbest。

Step3随机生成r。r的范围是[0,1]。

Step4由式(8)计算粒子位置。

Step5使用式(9)更新所有粒子的位置。

Step6使用目标函数评估所有更新的粒子。

Step7如果粒子超过下限或上限，则在下限和上限范围内随机生成新粒子。

Step8更新pbest。比较粒子适用值(位置)与它的个体最优值pbest，如果优于pbest，则其pbest位置就是当前粒子位置。

Step9更新gbest。比较粒子适用值(位置)与群体全局最优值gbest，如果目前值好于gbest，则设置gbest位置为当前粒子位置。

Step10重复Step4～Step9，直到找到最终的全局最优值或达到最大迭代次数。

3 基于SCSO算法的GRU预测模型

图2 SCSO-GRU模型架构

3.1 SCSO-GRU模型训练

SCSO算法优化过程可看作一个时变动态系统，迭代次数看作为离散的时间值，系统状态可视为每次迭代的最优解。训练之前需要确定测量方程、更新方程和初始状态。GRU预测模型的目标是使模型的预测值与实际值的误差尽可能小，也就是使其目标函数最小化,如式(10):

(10)

其中，y′t为实际值，yt为系统的输出值，T为时间序列的长度。

目标函数即测量方程，更新方程由式(1)～式(5)组成。在测量方程、系统更新方程以及初始状态都已知的情况下，SCSO算法可求出系统状态最优解。基于SCSO算法的GRU神经网络参数优化的步骤如下：

1)系统状态初始化。根据GRU的参数和式(1)～式(5)计算GRU的输出值y。以误差范围确定系统初始状态的定义域(搜索空间)作为系统的约束条件(即粒子位置的上下边界)。在其定义域内随机生成种群的方式进行初始化。令粒子总数为pn，迭代总数为MI。

2)计算初始状态个体和群体最优解。使用测量方程式(10)评估种群中的每个粒子，从中选择最优的粒子作为群体最优粒子，同时记录对应的最优y值。

3)更新个体和群体最佳粒子。由粒子更新公式(10)对个体最优粒子进行更新(若某个粒子不满足约束条件，则约束条件下随机生成新粒子)，使用测量方程评估所有更新的粒子，通过比较选出本次迭代的群体最优粒子，并将其与上次迭代的群体最优粒子进行对比，将更优的粒子和对应更优的y保存下来。

4)根据迭代次数k判断算法是否满足终止条件，如果不满足终止条件，则重新返回到步骤3。

5)算法终止。返回群体最优的粒子和系统的输出值y。

3.2 构建SCSO-GRU预测模型

本文在Windows 10系统环境下，使用Python 3.7和Keras深度学习框架搭建一个GRU循环神经网络模型。设计的GRU网络结构由1个输入层、1个隐藏层和1个输出层组成。结合图3可知，其具体的预测步骤如下：

1)数据预处理和样本划分。通过对流量样本数据进行最小值最大值标准化(归一化)处理，使样本数据处于[0,1]。这样处理可对方差非常小的属性增强其稳定性，也可维持稀疏矩阵中0的条目，样本数据标准化处理如式(11):

(11)

其中，Xmax与Xmin分别表示样本数据中的最大值和最小值。

将经过处理之后数据的90%组数据作为训练集，用于GRU神经网络模型的训练，余下的10%组数据作为测试集。

图3 SCSO-GRU网络流量预测模型

2)确定GRU网络的输入层单元个数m，输出层单元个数n和隐藏层单元个数l及隐藏层参数。将每批m个变量作为网络输入X={xi|i=1,2,…,m}，n个变量作为输出Y={yi|i=1,2,…,n}，隐藏层单元个数通过多次试探实验来决定。本实验中设m=24、n=1，即通过每批24 h的网络流量数据预测未来1 h的网络流量值。

3)模型训练过程参数设定。训练过程参数主要有batchsize(批处理大小)、iteration(迭代次数)和epoch。其中，batchsize为一次训练所选取的样本数，其大小影响模型的优化程度和速度；iteration即iter，一次iteration是batchsize个训练数据前向传播和反向传播后更新参数的过程，设定为500次；epoch是指所有训练数据前向传播和反向传播后更新参数的过程，即所有数据集训练一遍。除iteration参数外，其他参数通过SCSO算法确定，使模型收敛于全局最优。

4)网络流量预测。使用训练好的GRU模型对测试集数据进行预测。

5)预测模型误差判定。对于网络模型预测结果，先进行反归一化处理还原流量数据形式，对比测试集真实结果，再采用3种误差分析方法验证其预测精度，即均方根误差(Root Mean Square Error, RMSE)，平均绝对误差(Mean Absolute Error， MAE)和对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error, SMAPE)。其计算公式如下：

(12)

(13)

(14)

其中,y′i为序列样本的实际值，yi为预测值，n为样本总数。

4 结果分析

本文通过来自The UCI Network Data Repository的真实数据集训练SCSO-GRU模型并验证其预测性能，该数据集是英国学术网络主干中的聚合流量，统计了2013年11月9日早上9点半-2014年5月20日下午4点半之间每小时的网络流量，共计得到1657个样本。选择前90%的样本作为训练集，构建网络流量学习模型，后10%的样本作为测试集分析模型的性能，从预测精度和算法收敛效率2个方面验证其性能。

1)预测精度。如图4所示，将采用传统的BPTT算法训练的LSTM和GRU网络模型与本文提出的SCSO-GRU网络模型对网络流量值的预测结果曲线图进行对比。从该图可看出，传统的LSTM模型预测曲线虽然能反映网络流量的变化趋势，但是与真实值曲线拟合得不太理想；GRU模型相比LSTM模型精度有所提升，但在极值处的预测效果还是比较差；虽然SCSO-GRU对凹凸点的预测也不太准确，但比前2种模型的预测效果好很多，它能更好地跟踪网络流量的变化趋势，实现了更精确的预测。

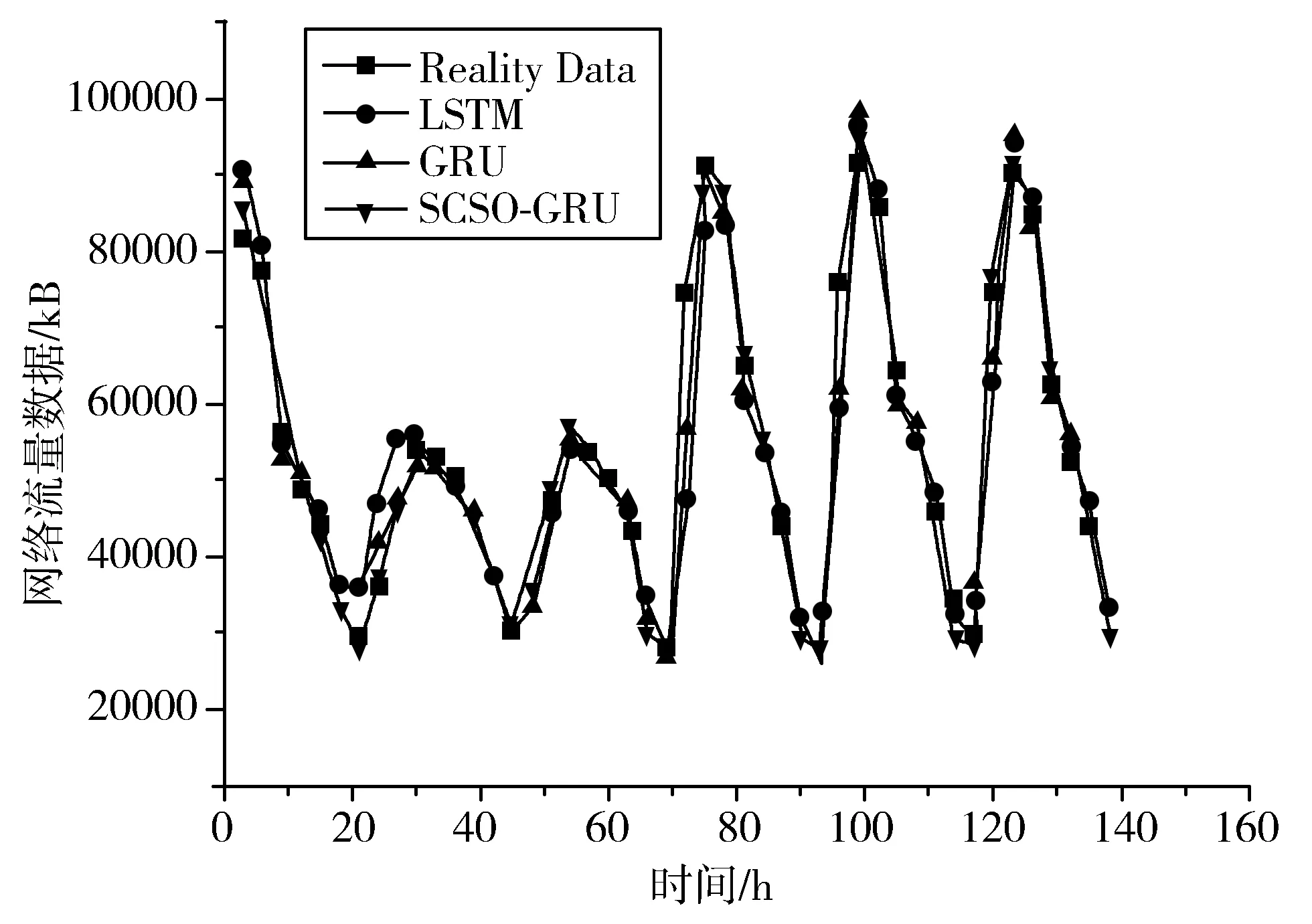
图4 SCSO-GRU网络流量预测模型

为进一步比较LSTM、GRU和SCSO-GRU这3种模型的预测效果，表1计算出了这3种模型的平均预测误差。RMSE、MAE和SMAPE。从表中可以看出，SCSO-GRU模型的预测结果误差小，可判定其预测值要明显优于传统的LSTM和GRU模型。从SMAPE的角度进行评价，传统的LSTM的结果为0.0585，GRU的结果为0.0459，GRU优于LSTM，而SCSO-GRU模型的结果为0.0307，优于LSTM和GRU的预测误差。

表1 几种预测误差对比

2)收敛效率。实验结果如图5所示，从最终的平均绝对误差上分析，GRU、SCSO-GRU模型的稳态相对误差均低于LSTM模型，说明前两者在预测精度方面要优于后者。从收敛速度方面考虑SCSO-GRU模型的误差收敛速度最快，其初始误差要明显小于其他2种模型，在经过将近100次的迭代之后，就能收敛于最优的误差值，而LSTM模型和GRU模型分别要到第450次迭代和第300次迭代之后平均绝对误差曲线才趋于平稳。因此SCSO-GRU模型可收敛到更小的稳态误差值，且收敛速度最快，具有更高的效率。

图5 3种不同模型在训练数据集上的误差收敛曲线图

5 结束语

网络流量时序数据具有复杂突变的特性，使用GRU神经网络进行时间序列预测可以得到较理想的效果。但传统GRU模型在进行训练时，其采用的BPTT算法易收敛于局部最优值，预测效果还不理想。本文使用了更加简化易于实现的基于正余弦的群优化算法(SCSO)优化GRU神经网络的网络流量预测模型(SCSO-GRU)。对GRU网络进行学习训练，并使用SCSO算法优化模型参数，用于网络流量的预测。实验结果表明，SCSO-GRU预测模型具有较好的预测精度，可以准确地把握网络流量的变化趋势，而且还有良好的收敛效率。若把该模型应用到网络流量管理与规划中，将有助于降低网络流量拥塞的频率，提高网络资源的利用率。