基于SVM的河北省平原区水电转换系数内插预测研究
2020-04-23岳士茹郄志红刘印良
岳士茹, 郄志红,刘印良,吕 旺,兰 凤
(1.河北农业大学 城乡建设学院,河北 保定 071001;2.河北省水资源研究与水利技术试验推广中心,河北 石家庄 050061)
河北省水资源总量严重不足,多年平均水资源量205亿m3,亩均水资源占有量211 m3[1-2]。随着经济的快速发展,水资源供需矛盾日益突出,迫切需要改革水资源管理方式,推行水资源费改税不可避免。2016年3月,河北省被确定为全国唯一的水资源税改革试点,要求为国家提供可复制、可推广的经验和模式以全面征收水资源税[3-4]。河北省共104万眼机井,大多没有安装计量设施,无法直接获取用水量数据,因此采用“以电折水”方法对农业用水实现间接计量是1种经济、实用、有效的解决办法。
“以电折水”方法是根据农业用水的特点以及用水中存在的问题提出的,国外还没有相关报道[5-7]。在国内,尹世洋[8]通过实验分析了影响水电转换系数的主要参数,得出地下水位埋深越小、含水层富水性越好的地区水电转换系数越大;王晓东等[9]通过实验分析了功率、流量、扬程与水电转换系数之间的关系,从理论上进行了验证并校准;王剑永[10]对水电转换系数的影响因素和邯郸市成安县不同灌溉时段的实测数据进行了分析,提出了水电转换系数的修正方法并分析其误差情况。近年来,支持向量机(SVM)由于结构简单,能很好地解决小样本、高维度的非线性问题而得到了相关领域的广泛关注[11-13]。本研究构造了基于SVM的水电转换系数的预测模型,并以实测数据对模型的准确性进行了验证。
1 机井样本调查与水电转换系数计算
1.1 典型机井的选取
河北省水利推广中心在河北省平原区选取了377眼典型农用浅井进行实测,为使选取的典型机井有代表性,能充分体现水文地质条件、机井装置效率等的差异,原则上按照每8万a灌溉面积布设1个典型机井。再综合考虑深浅井分布、种植结构、机泵类型等情况,要求每个县实测机井数量不少于5眼,并确保分布相对均匀[14]。河北省平原区实测浅井分布图如图1所示。

图1 河北省各行政区实测浅井分布图Fig.1 Distribution of measured shallow wells in various adminisstative regions of Hebei province
1.2 水电转换系数的计算
“以电折水”是通过计算机井用于灌溉消耗的电量来推算灌溉用水量,从而计收水费的1种方法。水电转换系数,就是水泵的总出水量与总用电量在一定时段内的比值,一般用下式计算[10]:

式中,TC是水电转换系数,单位是m3/kWh;AW是机井出水量稳定后某一时段的总出水量,单位是m3;AE是同一时段的总耗电量,单位是kWh。
选取典型农用机井,通过测算其水电转换系数,建立单位耗电量与提水量的关系,就可以根据某个典型农用机井某一时段用电量推算同时段用水量。
1.3 水电转换系数的影响因素分析
水电转换系数受多种因素影响,包括各地的水文地质情况、地下水位埋深、井深、井龄、泵龄等。地下水位埋深越大的地区,其水电转换系数一般越小[8],结合邯郸市临漳县的实测数据(图2)也说明了这一点。水文地质条件较好、含水层富水性较好的地区其相应的水电转换系数也越大[8];而机井、水泵使用时间越长,随着设施的老化,使得井泵不配套,机井出水量减少,其相应的水电转换系数也会减小。

图2 邯郸市临漳县浅井水电转换系数与地下水位埋深关系图Fig.2 Relationship between hydroelectric conversion coefficient and groundwater table depth in shallow wells of Linzhang county, Handan city
本研究通过调查资料以及实地测算,了解各行政区的相关情况,具体如下:
(1)地下水位埋深 本研究用GoogleEarth导出各井位处的地面高程,根据保定市监测井的数据[15]由ArcGis内插求得各机井的地下水位,用各井位处的地面高程减去地下水位求得各机井的地下水位埋深,河北省平原区浅井的地下水位埋深情况见图3,由图3可得石家庄、邯郸的部分地区地下水位埋深较大,其相应的水电转换系数较小,而秦皇岛、唐山等地的地下水位埋深较小,相应的水电转换系数也较大[8]。

图3 各行政区浅井地下水位埋深分布图Fig.3 Distribution of groundwater depth in shallow wells in various administrative areas
(2)水文地质条件 河北省水文地质条件自西向东,即自太行山区向平原中部的石家庄、衡水的部分地区以至滨海的秦皇岛市、唐山市、沧州市的部分地区呈现水文地质条件的水平方向的分带性。自西向东在含水层的岩性、分布、厚度和地下水的化学成分,运动特征等方面均有显著变化;而在南北方向内,则变化较小。
含水层的岩性和成分,自山区向平原东部由以粗颗粒为主变为以细颗粒为主;含水层的层次数目,在平原西部的石家庄市、保定市部分地区较少,或1个或2个;但每个含水层的厚度均较大(20到30 m或更多)。向东则含水层层数增多,但每层厚度减小(5、6 m或10数m)。在含水层富水性较好的保定市定兴县、秦皇岛市水电转换系数相对较大,而含水层富水性较差的唐山市等地区,其水电转换系数相对较小。
(3)井深 根据相关规定,平原区一般把井深小于150 m的机井叫做浅井。农用机井深度一般较浅。各行政区机井井深、井龄、泵龄大体情况见表1。可见,除邢台、廊坊市井深相对较深以外,其它各行政区农用机井深度一般低于100 m。机井深度和地下水位埋深也有一定关系,地下水位埋深较深的地区机井深度一般也较深,其对应的水电转换系数相对较小。
(4)井龄、泵龄 由表1数据可得,各行政区农用机井井龄相对较长,而唐山、保定市机井使用年限较其它地区更长,这也使得唐山市机井水电转换系数相对较低;从泵龄看,各行政区所用水泵泵龄一般在4年左右,衡水市农用机井所配水泵泵龄相对较长,这也是衡水市机井水电转换系数偏低的1个原因。

表1 各行政区机井井深以及井泵龄相关情况Table 1 Relevant situation of well depth and well pumping age in each administrative area
1.4 不同区域水电转换系数分布情况
本研究对河北省平原区各行政区浅井实测的水电转换系数进行整理,计算其平均值及标准差,结果如表2所示。由表2可得,河北省水电转换系数平均值为3.49,标准差1.57,说明全省水电转换系数分布不均,偏离平均值程度较大。从各市来看,秦皇岛市水电转换系数为5.51,相对较大,标准差为2.5,标准差较大,说明秦皇岛市水电转换系数平均值代表性较小,离散程度较大;唐山市和邯郸市系数分别为2.78和2.51,相对偏小,其标准差分别为0.46和0.92,说明平均值代表性较大,离散程度较小。
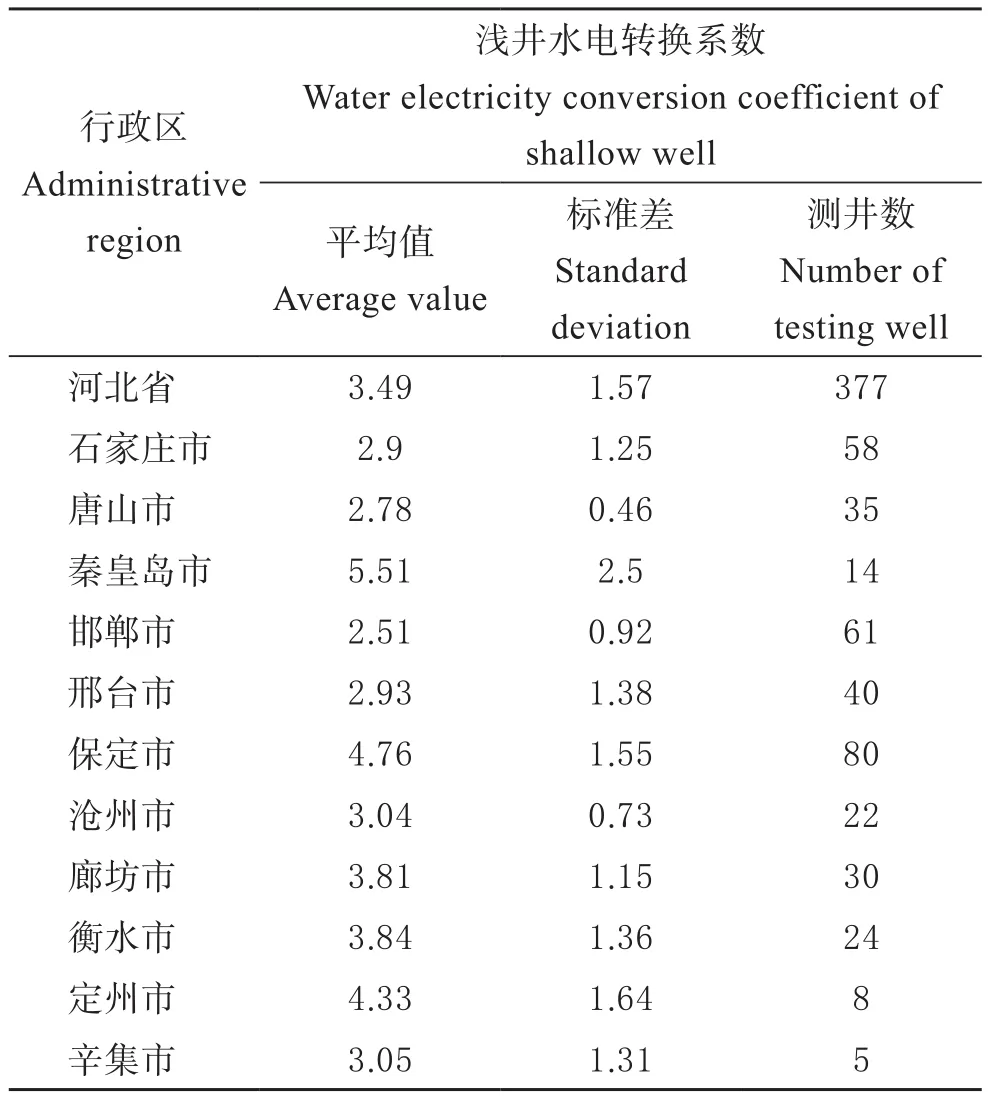
表2 各行政区浅井水电转换系数测算成果Table 2 Results of calculation of conversion coefficient between consumed electricity and pumped water of shallow wells in various administrative regions
2 水电转换系数的SVM模型
2.1 基于SVM的水电转换系数预测模型
支持向量机算法目前主要应用于分类和回归两方面。本研究针对水电转换系数求解的问题,主要利用其回归函数建立基于支持向量机的分析方法。具体可以描述为图4所示的模型。
该模型的输出变量Y是水电转换系数,输入变量X是水电转换系数的影响因素:地下水位埋深x1、井龄x2、泵龄x3、机井所在位置(纬度x4、经度x5),即:{(xi,yi),i=1,2,…,N} 其中xi∈Rn为输入向量,yi∈Rn为与xi相对应的输出向量。
对于上述模型,SVM使用回归函数y=f(x)=wx+b将实际问题通过非线性映射转换到高维特征空间,从而在原始空间中实现线性回归。假设所有训练样本数据都由精度ε下的线性拟合函数表示,同时考虑到允许误差的情况,引入松弛变量ξi≥0和≥ 0,即

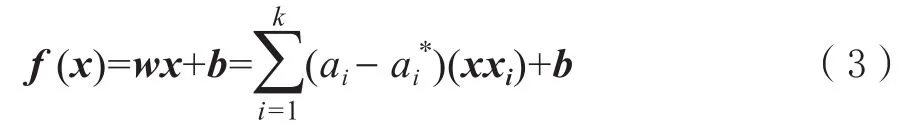
对于非线性问题,可以通过非线性变换将原问题映射到高维特征空间进行求解。
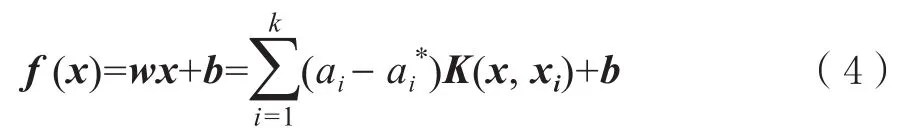
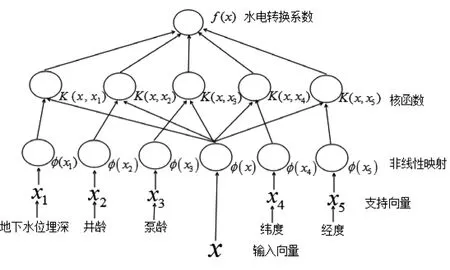
图4 水电转换系数的SVM模型Fig.4 SVM model of conversion coefficient between consumed electricity and pumped water
2.2 水电转换系数的SVM模型基本参数及优化
式(4)中,K(x,xi)为核函数,本研究选择径向基核函数,即

相应的参数有惩罚因子C,不敏感损失函数的参数ε,核函数的宽度σ。惩罚因子C控制模型的复杂性和逼近误差的折中。参数C越大对数据的拟合程度越高,但是泛化能力越低;C越小,训练误差变大。不敏感损失函数参数ε影响支持向量的数量。参数ε增大,导致支持向量的数量减少;而ε较小,支持向量的数量越多,同时使计算量变大。核函数的宽度σ影响高维特征空间中样本数据分布的复杂性,σ越小局部极小领域的样本差异越明显。参数的不同取值对SVM的拟合和泛化性能有直接影响。通过经验分析不同参数对拟合和检验精度的影响,进行交叉试算找到1组合适的参数,使模型能得到较好的实际效果。
2.3 计算结果分析
本研究采用河北省水利推广中心对河北省平原区各浅井水电转换系数的测算结果,按式(6)对样本数据进行归一化处理以消除量纲的影响。

为保证预测效果,根据各行政区实测机井数选择训练样本和测试样本,具体如下:由于辛集市实测数据较少,回归分析不显著,故将其并进石家庄市,每7眼井选择1眼预测井;廊坊每6眼井选择1眼预测井;定州每4眼井选择1眼预测井;其余各行政区每5眼井选择1眼预测井。取参数C=100,ε=0.2,σ=0.08,将其代入SVM回归程序,得水电转换系数预测效果如图3。SVM预测误差情况和以训练样本水电转换系数平均值代替每眼井水电转换系数的误差比较情况见表3和表4.
从表3和表4可以看出,SVM模型预测各行政区水电转换系数得到的结果中,训练样本最大误差为17.32%,最小误差0.01%,平均误差5.88%;预测样本最大误差78.81%,最小误差0.17%,平均误差19.14%。而用训练样本的平均值代替每眼井的水电转换系数,训练样本最大误差达326.72%,最小误差为0.17%,平均误差34.30%;预测样本最大误差99.20%,最小误差0.72%,平均误差22.53%。基于SVM模型的全省平均预测精度较后者提高17.71%。对水电转换系数分布离散性较大的区域,如秦皇岛、邢台市,用平均值代替每眼井的水电转换系数误差较大;而对离散性较小的区域,如唐山市,用平均值代替每眼井的水电转换系数误差相对较小。2种方法预测误差分布情况见表5。
由表5可得,SVM模型训练误差低于10%的达90%以上,而采用平均值预测训练误差低于10%的仅占24.03%,SVM模型训练误差明显小于后者,优势较为显著。从预测误差来看,SVM模型预测误差低于30%的达80%以上,预测精度有一定提高。结合图5总体来看,SVM模型拟合程度较好。

表3 各行政区浅井水电转换系数SVM预测误差Table 3 SVM prediction error of shallow well conversion coefficient between consumed electricity and pumped water in each administrative area

表4 以训练样本平均值代替各井水电转换系数误差情况2种预测方法误差分布情况Table 4 Replacing the prediction error of conversion coefficient between consumed electricity and pumped water of each well with the average value of training samples
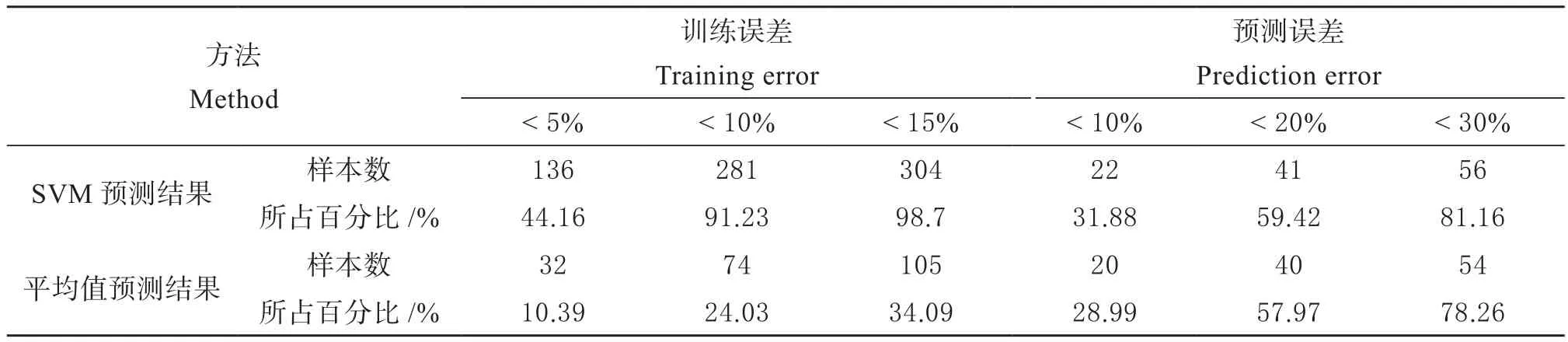
表5 2种方法预测误差情况对比Table 5 Comparison of prediction errors between the two methods

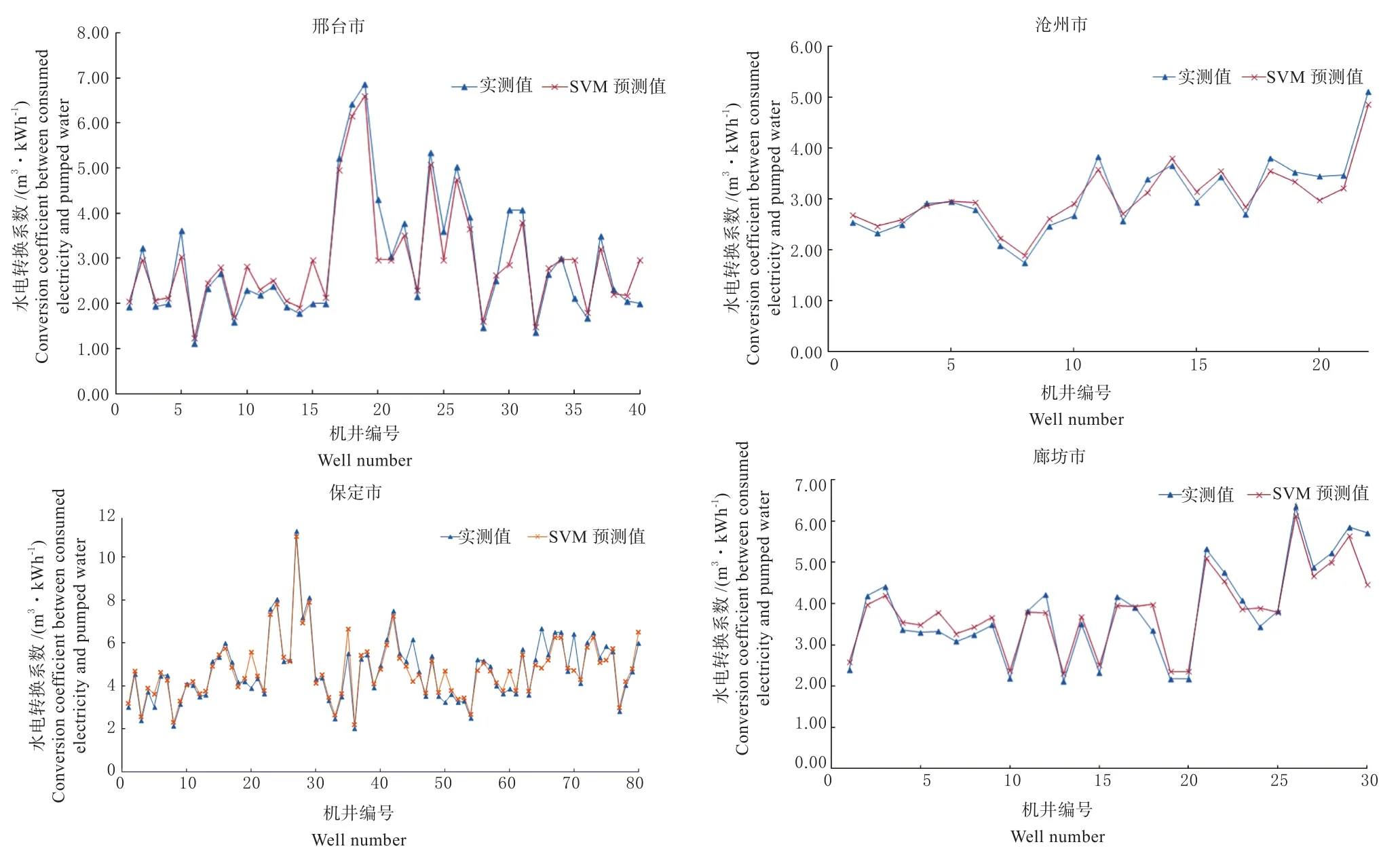
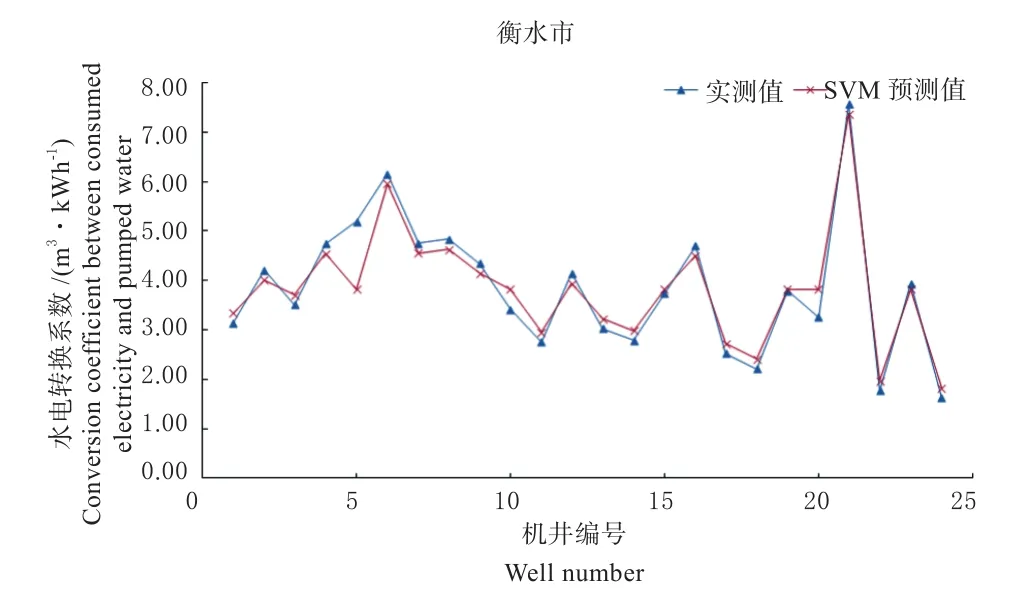
图5 SVM预测效果图Fig.5 prediction effect of SVM model
3 SVM模型产生误差原因及改进措施
分析产生上述误差的主要原因大体如下:
(1)样本数量少。本次调查的浅井样本数不到浅井总数的0.4‰,其代表性有限。对于水电转换系数离差较大的邯郸、邢台、秦皇岛等地,样本数显得尤为不足。
(2)农用机井质量差异较大,模型中仅考虑了井龄和泵龄的影响,而未考虑成井质量及特殊故障因素引起的动水位降深不同的影响。
(3)部分机井水泵配套不合理而导致机井效率降低。
(4)未考虑供水管道长短及出水点剩余压力不同的影响。
针对以上原因,提出如下几点改进措施:
(1)补充监测井的数量,特别是水文地质条件差异较大,水电转换系数离差较大的地区更要加大监测井的数量。
(2)补充调查监测项目,对机井的质量和异常情况、机泵配套度及供水区域规模等进行评价和诊断,将这些因素的评价值作为SVM模型的输入项,以优化预测模型。
(3)在实际应用中,还需加强实时监测,根据现有数据及监测数据,以地下水位埋深、井龄、泵龄、机井所在位置以及对机井配套度、机井质量和异常情况、供水区域规模等的评价值作为输入变量建立SVM模型来更精确地预测水电转换系数。
4 结论
本研究对河北省平原区浅井的水电转换系数进行分析,并用SVM模型对各行政区的水电转换系数进行内插预测,得出如下结论:
(1)基于初步调查数据的河北省浅层机井水电转换系数平均值为3.49,其标准差为1.57,其分布离散性较大。不同行政分区或水资源分区间水电转换系数均有明显差异。
(2)以地下水位埋深、井龄、泵龄、机井位置为输入变量,水电转换系数为输出变量建立的SVM模型具有较好的训练精度,较之按区域水电转换系数均值预测的方法的预测精度提高17.71%。
(3)机井调查监测的样本数量、机井质量、井泵配套合理性以及机井供水规模等均对水电转换系数有重要影响,考虑以上因素进一步优化SVM模型将有助于提高预测精度。
