大学物理实验中测量不确定度的分析研究*

冯明春 王玉杰

(滁州学院机械与电气工程学院 安徽 滁州 239000)

测量不确定度是指测量结果变化的不肯定，是表征被测量的真值在某个量值范围的一个估计，是测量结果含有的一个参数，用以表示被测量值的分散性[1,2].测量不确定度的定义表明，一个完整的测量结果应包含被测量值的估计与分散性参数两部分.例如，被测量Y的测量结果为y±u，其中y是被测量值的估计，u为被测量的不确定度.文献[3～5]着重分析了不确定度的一些理论；而本文在不确定度理论基础上再结合具体实验数据，分别对力学、热学和光学实验中所对应的弹性模量、液体表面张力系数和牛顿环实验中平凸透镜的曲率半径这3个实验测量结果的不确定度进行了分析讨论，这有助于教师实验教学和学生分析实验数据，使得研究更有意义.

1 分析过程

根据测量不确定度的定义，在测量实践中如何对测量不确定度进行合理的评定，这是必须解决的基本问题.对于一个实际测量过程，测量不确定度的来源有多个，这些不同来源的不确定度在计算方法上只有两类，一类称为A类分量，它是用统计学方法计算的分量，是随机误差性质的不确定度；另一类称为B类分量，是用非统计方法评定的分量，是系统误差性质的不确定度[6].计算不确定度，常用计算标准差去表示，称为标准不确定度.

1.1 直接测量值的标准不确定度的A类分量uA(x)

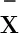
取x的标准不确定度的A类分量为

(1)

1.2 直接测量值的标准不确定度的B类分量uB(x)

设x误差的某一项的误差限为Δ，其标准差

则标准不确定度的B类分量

(2)

式(2)中，k称为包含因子，k值与x的分布有关，其常用分布及其k值如表1所示.

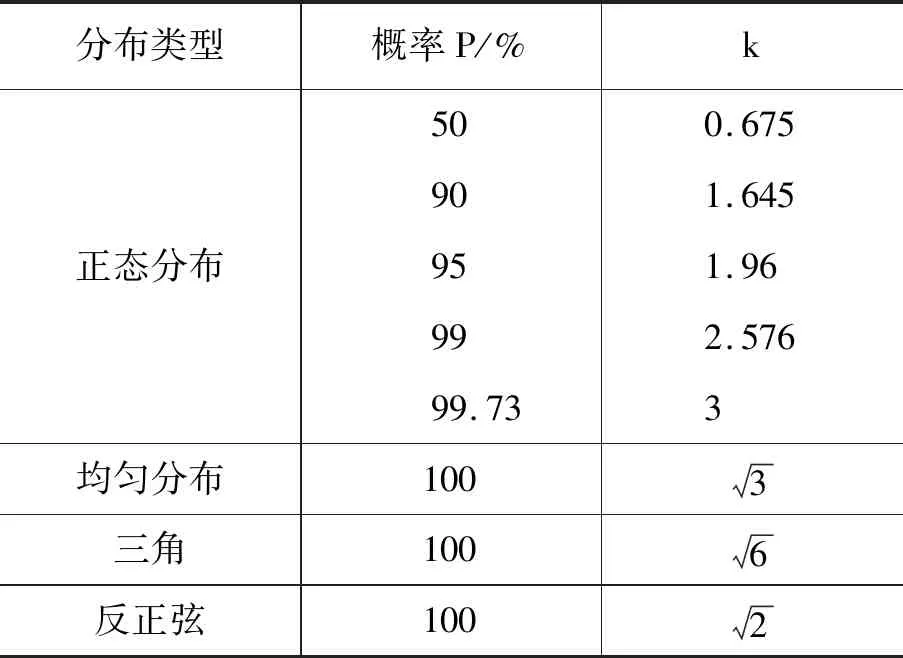
表1 常用分布及其k

1.3 合成标准不确定度uc(x)或uc(y)

对某一物理量测量之后，要计算测量值的不确定度，由于其测量值的不确定度来源不止一个，所以要合成其标准不确定度.

对于直接测量，设被测量X的标准不确定度的来源有m项，则合成标准不确定度uc(x)为

(3)

式(3)中的u(x)可以是A类评定或B类评定.

对于间接测量，设被测量Y由n个不相关的直接被测量x1，x2，…，xn算出，它们的关系为y=y(x1，x2，…，xn)，各xi的标准不确定度为u(xi)，则y的合成标准不确定度uc(y)为

(4)

1.4 不确定度的报告

Y=y±uc(y)

(5)

式(5)就是被测量的不确定度的表现形式.

2 实验分析

2.1 弹性模量的标准不确定度

金属丝弹性模量E的表达式为[6]

(6)

在式(6)中，F为外力，l为金属丝的长度，d为金属丝的直径，这3个物理量都易测量；由于金属丝的伸长量δ太小，不容易测量，所以在计算金属丝的弹性模量时，关键是如何解决测量金属丝伸长量δ的问题.那么，在实际实验中，巧妙地利用了光杠杆装置来测量伸长量δ[6]，实验装置如图1所示.

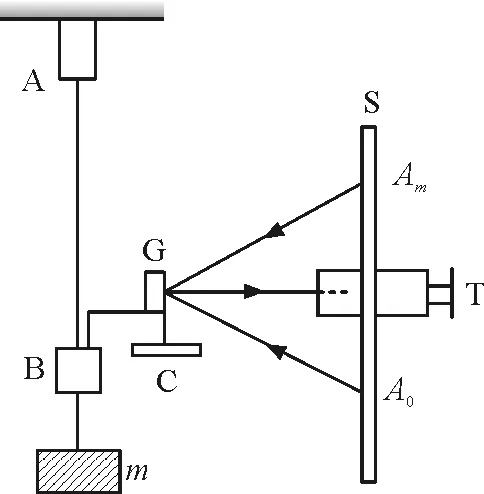
图1 弹性模量实验图

在图1中，光杠杆G前足尖到两后足尖连线的垂直距离为d1，光杠杆平面镜到直尺S的距离为d2，加砝码m前后望远镜中直尺的读数为A0和Am，根据几何关系得到金属丝伸长量δ为

(7)

根据式(6)、式(7)以及F=mg，得到伸长法测金属丝弹性模量E的公式为

(8)

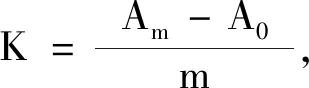
(9)

根据式(9)，可以推导出弹性模量E的标准不确定度u(E)为

(10)

在此实验中测量的实验数据，如表2所示.

在表2中一个砝码质量m=360 g，根据表2数据采用3种方法来计算K.

(1)由逐差法计算求得

2.66×10-3m·kg-1

表2 弹性模量实验数据

(2)由图像法拟合求得

根据表2实验数据绘制图2.

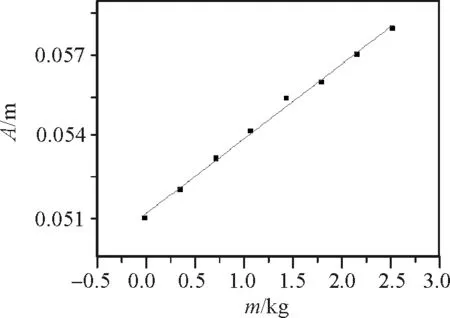
图2 图像拟合法

(3)由最小二乘法求得

令xi=mi，yi=Ai进行直线拟合(y=a+bx)，此b值就是K，其中

∑xi∑x2i∑yi∑y2i∑xiyi10.0818.1440.438480.024070.56689

则令

计算得到

1.2.1.1 造口护理指导 示范更换造口袋的护理程序，指导患者造口袋渗漏的判断和更换时机，观看造口袋的护理录像，发放造口护理手册;指导患者使用收集袋的排放方法以及到厕所排放的方法，学会不同的排放气体的方法;指导患者正确清洁造口袋;根据造口形状、患者经济条件推荐不同的造口辅助产品，以满足不同的需求;让患者了解造口的各种并发症的症状表现，示范处理方法，做到早期预防，告知患者定期随诊的重要性;指导选择合适的造口袋，造口袋使用的注意事项，告知患者购买途径以及造口袋的储存方法及注意事项。

可以看出，3种方法求得的K误差不大，再结合其他实验数据l为38.52 cm，d1为9.800 cm，d2为161.50 cm，d为0.642 mm，根据式(9)求得E为

由测量仪器的误差限可知

采用的都是均匀分布的B类分量，根据式(10)，计算得到E的标准不确定度

u(E)=0.770×1010N·m-2

那么，金属丝的弹性模量E的标准不确定度报告为

E±u(E)=(14.46±0.77) ×1010N·m-2

2.2 液体表面张力系数的标准不确定度

实验装置如图3所示.

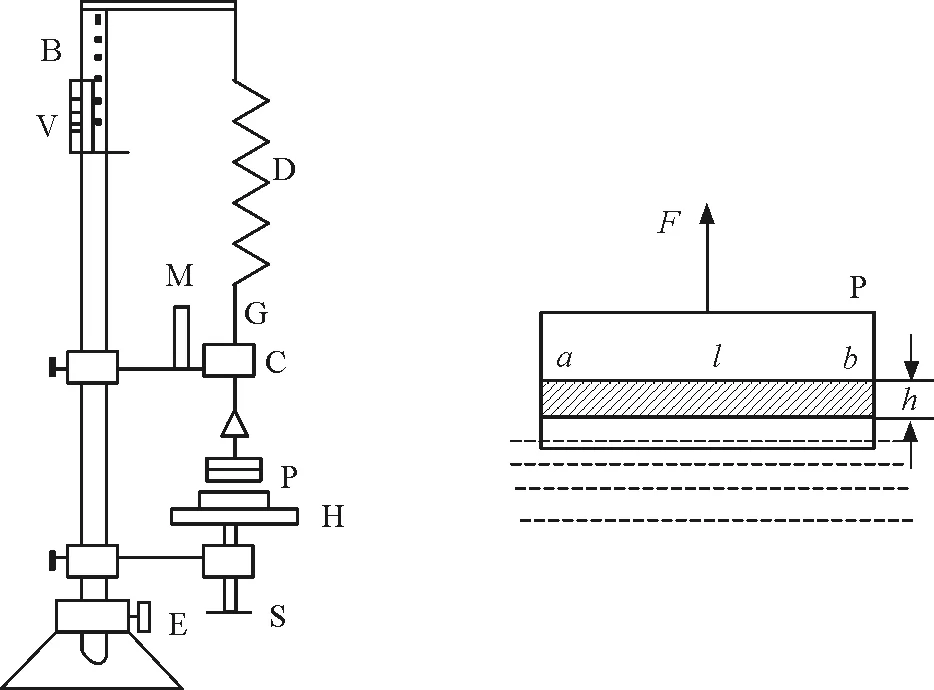
图3 实验示意图

在实验中金属框P中间拉一金属细丝ab，将框及细丝浸入水中后慢慢地将其拉出水面，在细丝下面将带起一水膜，当水膜即将破裂时，则有

F=W+2γl+ldhρg

(11)

在式(11)中，F为向上的拉力，W为框所受重力和浮力之差，l为细金属丝的长度，d为金属丝的直径即水膜的厚度，h为水膜被拉断前的高度，ρ为水的密度，g为重力加速度.ldhρg为水膜的重量，因为张力大小与长度成正比，同时水膜有前后两面，所以式(11)中张力为2γl.从式(11)可得水的表面张力系数表达式为

(12)

在此实验中，约利秤的劲度系数k为0.97 N·m-1，测量液体表面张力系数的其他实验数据如表3所示.

表3 液体表面张力系数实验数据

在表3中，s1为金属丝刚好到水面时的位置，s2为水膜刚好破裂时的位置，L0为水膜刚好破裂时B柱上的位置，L1为当转动E使金属框缓慢下降到G回到零点(G的横线、横线的像和镜面标线重合位置)时B柱上的位置，可知水膜高度

h=|s2-s1|

F-W=kL=k|L1-L0|

根据表3数据，再代入式(12)可求得水的表面张力系数为

51.99×10-3N·m-1

由测量仪器的误差限可知

采用的也都是均匀分布的B类分量，由式(12)可知，γ的标准不确定度为

0.66×10-3N·m-1

那么，水表面张力系数的标准不确定度报告为

γ±u(γ)=(51.99±0.66)×10-3N·m-1

2.3 曲率半径的标准不确定度

牛顿环仪是由平凸透镜L和磨光的平玻璃板P叠合安装在金属框架F中构成的，如图4所示；测量的实验数据[7]，如表4所示.

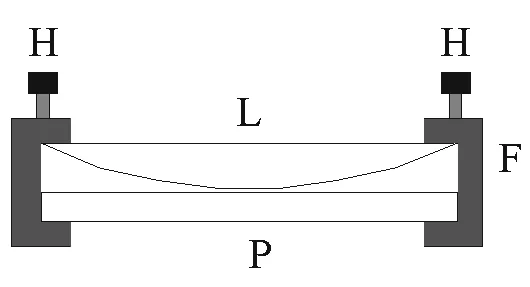
(a)实验装置

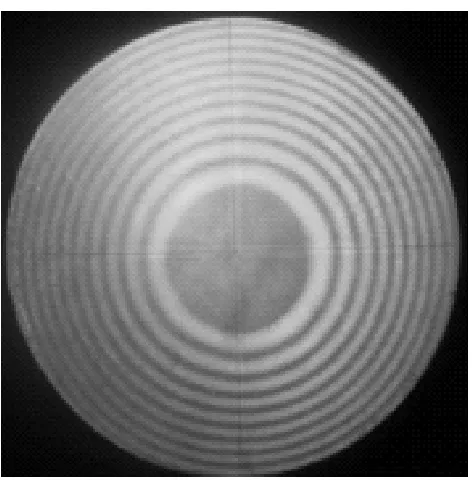
(b)牛顿环干涉图样

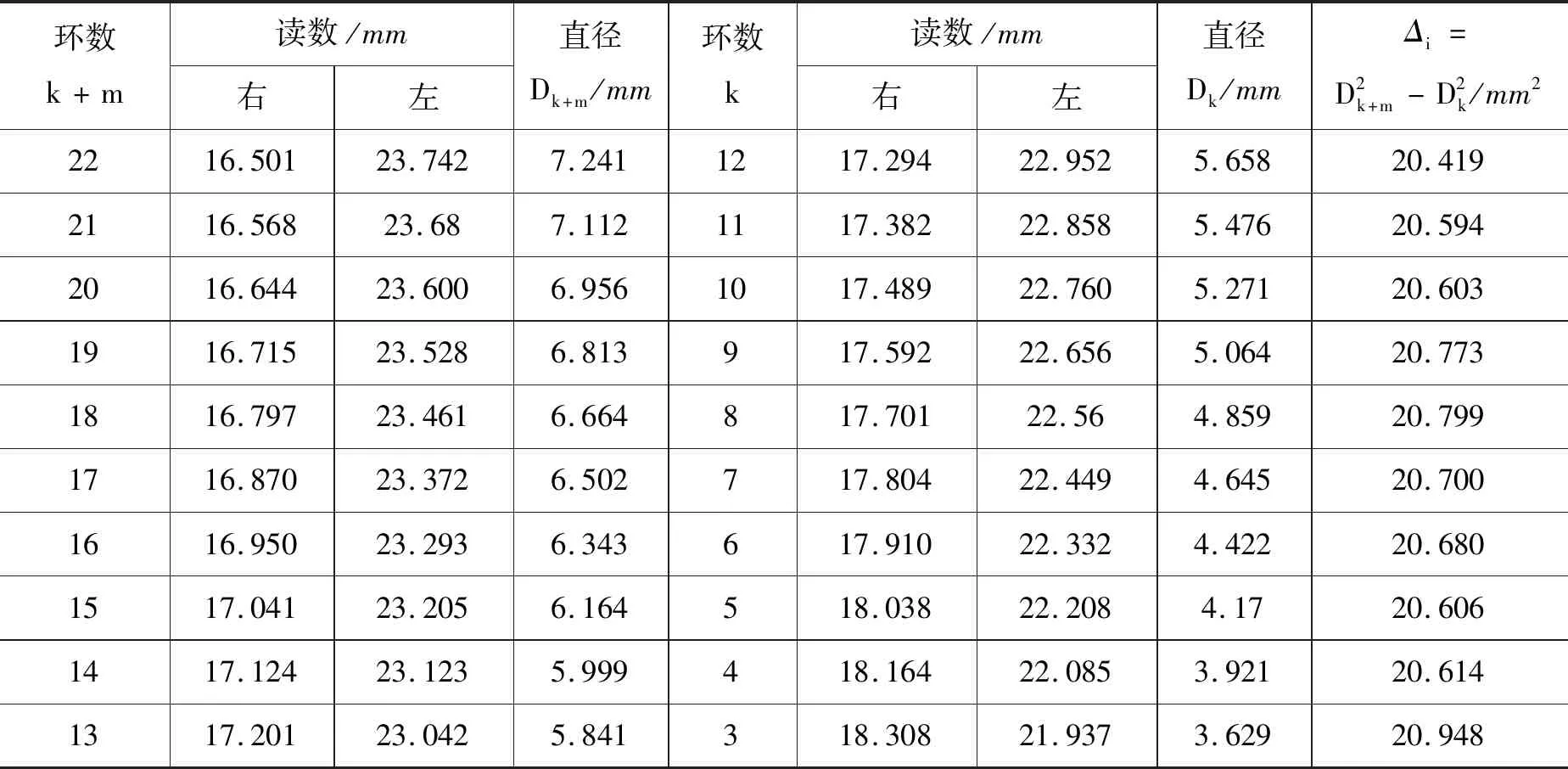
表4 牛顿环实验测量数据

根据表4中数据，可以得出

其中，环数差m=10，波长λ=589.3 nm，根据曲率半径公式

计算得到R为877.1 mm.

下面计算曲率半径R的标准不确定度u(R)

Δ的A类分量为

Δ的B类分量为

其中Δins=0.01 mm为移测显微镜的最小分度值.

合成后

同时，由于视觉疲劳所造成的环数误差u(m)，不妨假设u(m)=0.1；再结合u(λ)=0.30 nm(钠双黄线波长λ1=589.0 nm和λ2=589.6 nm导致)，可得合成标准不确定度为

u(R)=

测量结果为

R±u(R)=(877.1±9.9) mm

而厂家提供的凸透镜曲率半径标准值为

AR=855.1 mm

根据测量结果

R=877.1 mm

与其标准值

AR=855.1 mm

可知，两者之差不超过其标准不确定度u(R)=9.9 mm的3倍[6]，即

|R-AR|≤3u(R)

则可以认为测量结果和标准值在测量误差范围内是一致的.

3 分析和讨论

金属丝弹性模量E的不确定度表达式

但用逐差法求解

时，分母体现出来的是16m，所以计算时

而不是

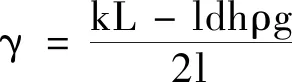
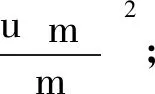
4 结论

在分析金属丝弹性模量E的标准不确定度u(E)和液体表面张力系数γ的标准不确定度u(γ)时，仅仅分析计算了B类标准不确定度作为总的不确定度，略去A类标准不确定度，主要是B类分量起主要作用；在分析曲率半径R的标准不确定度u(R)时，同时考虑了A类不确定度和B类标准不确定度；对于随机误差为主的测量情况，可以忽略B类标准不确定度，只分析计算A类标准不确定度作为总的不确定度.