采用响应面法的轿车驾驶员座椅的模态优化

苏仕见 ，徐元利，夏洪兵，胡海欧，刘国彬，张泽豫

(1.天津科技大学机械工程学院，天津 300222；2.中国汽车技术研究中心有限公司汽车工程研究院，天津 300300)

目前，汽车NVH(noise，vibration，harshness)性 能越来越受到用户的重视，汽车开发过程中振动和噪声的控制显得尤为重要.汽车整车振动噪声性能的控制往往从控制部件及总成的性能入手.座椅是汽车车身附件中的重要部件，人身体直接与座椅接触，汽车的振动都会通过座椅传递到人的身体[1].因此，汽车座椅的模态性能设计非常重要.文献[2]提出了采用模态贡献量的识别方法，找到对重要频响函数贡献较大的模态，从而对结构进行针对性地优化，达到了改善振动问题的目的.文献[3]基于有限元法和实验方法将考虑了蛇形弹簧预紧力的座椅骨架的模态进行分析和对比，发现蛇形弹簧的预紧力对座椅结构的弹簧振动固有频率影响较大，得到了蛇形弹簧在分析中合适的处理方式.文献[4]对汽车座椅骨架结构进行计算模态与实验模态分析比较，并结合质量分布方式对模态特性影响的数据对座椅进行尺寸优化.文献[5]基于TPA 传递路径分析和模态优化原理，在座椅骨架的横梁内焊接加强件，以提升局部刚度和强度，进而提高座椅的模态频率.

本文以某轿车的驾驶员座椅结构为研究对象，建立有限元模型，分析其模态性能.针对未达标的模态频率，在保证座椅结构总质量不增加的前提下进行模态优化.首先对座椅结构钣金件进行模态灵敏度分析，选取对座椅模态影响较大的板件作为设计变量，然后通过拉丁超立方实验设计构造样本模型，并拟合Kriging 响应面近似模型，最后基于Kriging 模型并利用遗传算法对座椅结构进行模态优化.采用响应面法和遗传算法相结合的方法对座椅结构进行模态优化，相较传统的结构优化方法具有实验次数少、效率高、优化结果可靠等优点.

1 驾驶员座椅有限元建模与分析

1.1 座椅有限元建模

基于HyperWorks 软件构建驾驶员座椅的有限元计算模型，如图1 所示.座椅模型含有钣金件和钢铸件，分别划分为四边形壳单元和四面体单元，综合考虑计算机的求解环境与计算精度，选择单元尺寸为5 mm.座椅骨架主要采用螺栓和焊点连接，螺栓连接用RBE2 刚性单元模拟，焊点连接采用ACM 单元模拟，模型焊点的间距取5～20 mm.模型共划分为30 943 个四面体单元和39 082 个壳单元，壳单元中含有三角形单元1 698 个，占壳单元总数的4.3%，符合计算要求.对划分的网格进行质量检查，结果显示其质量较高，亦满足仿真分析的要求.

图1 驾驶员座椅有限元模型Fig.1 Finite element model of the driver seat

1.2 材料参数与边界条件

本文研究的座椅骨架结构使用的材料是20 号钢，材料的力学参数见表1.座椅的边界条件是将4个滑轨下支架通过螺栓连接的方式固定在车身地板上，在有限元模型中，分别对这4 个支架的6 个安装点约束6 个自由度.座椅结构在进行模态计算时需要省略坐垫、靠背和头枕的蒙皮等模态贡献率较小的部件，并在这些省略部件对应的重心处增加配重，用CONM2 单元模拟.

表1 座椅结构的材料参数Tab.1 Material parameters of the seat structure

1.3 模态分析

1.3.1 模态分析理论

模态分析是研究系统振动特性的一种常用方法，系统各阶模态都包括振型、固有频率和阻尼等参数.对于多自由度系统，其微分方程如下：

由于在进行模态分析时，汽车驾驶员座椅结构的固有特性与外部的载荷和激励条件均无关，因此式(1)中F＝0，而C 在分析的过程中一般忽略.所以其方程简化为

由于弹性体的自由振动总可以分为一系列简谐振动的叠加，当发生谐振动时，即 U =α sin(ω t+φ )时，方程变形为

式中：α 是各点的振动幅值向量；ω、φ 是振型对应的圆频率和相位角.

式(3)是关于ω 的n 次方程，解方程可得到结构的n 个固有频率，每个固有频率都有一个相应的振型向量.

1.3.2 座椅结构模态分析结果

采用Optistruct 求解器计算座椅模型在0～40 Hz范围内的固有频率及振型.由于结构的固有频率越低，越容易被外界激励，即结构的低阶模态对结构的模态频率贡献率更大，所以在NVH 分析过程中主要关注结构的低阶模态频率.本研究中座椅结构的模态频率贡献率最大的是一阶X 向模态和一阶Y 向模态，并且这两阶模态较接近所研究轿车的怠速频率(18～23 Hz)，所以本文重点研究上述两阶模态，忽略其他模态.为了避免与轿车的怠速频率耦合，制定这两阶模态频率的目标值为24 Hz.模态分析结果见表2，振型如图2 和图3 所示.

表2 座椅结构模态特性Tab.2 Modal characteristics of the seat structure

图2 Y 向横摆模态Fig.2 Y-direction pendulum modal

为了确保后续座椅模态分析及优化结果的准确性，对该座椅结构进行模态测试并与仿真结果对比.将座椅的底座用螺栓连接在实验台上，采用多点激励、多点响应的方法进行约束状态下座椅模态实验，通过LMS Test.Lab 系统对模态参数进行识别.实验模态与有限元法计算模态的对比见表3，二者误差均小于3%，从而验证了座椅有限元模型的准确性.

通过模态计算和分析，发现初期设计的驾驶员座椅结构的X 向弯曲模态达到主机厂所制定的目标值，但是Y 向横摆模态低于目标值，因此需要对座椅结构的Y 向横摆模态进行优化.

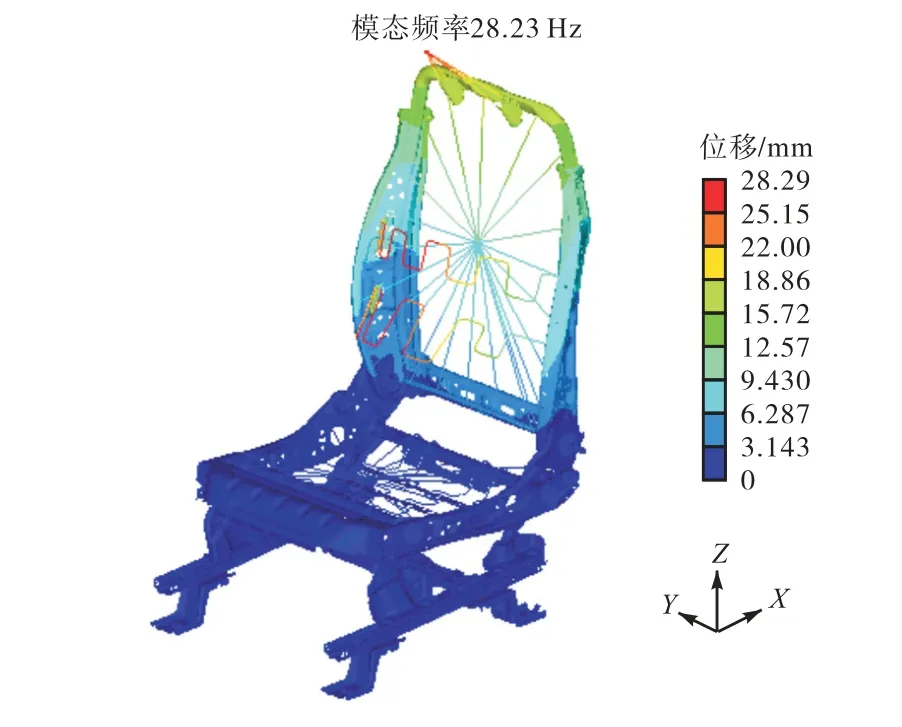
图3 X 向弯曲模态Fig.3 X-direction bending modal

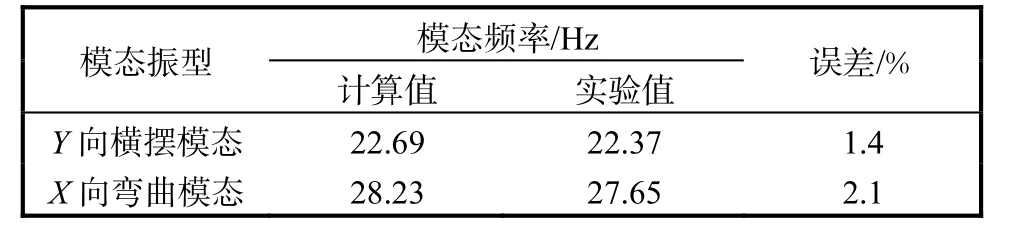
表3 实验模态与仿真计算模态对比Tab.3 Comparison between experimental modal and simulation modal

2 响应面模型的构建

2.1 响应面法

响应面法(response surface methodology，RSM)是一种将实验设计与理论统计相结合的优化方法，该方法通过抽取一系列的样本点，利用样本点的实际响应函数值构造有明确表达形式的多项式来近似表达隐式功能函数，通过在给定的设计变量空间内进行有限的实验设计，拟合出输出变量的全局逼近来代替真实的响应面[6-8].

2.2 设计变量的选取

驾驶员座椅结构由37 个部件组成，包括靠背上横梁管、靠背外侧侧板、靠背内侧侧板、坐垫侧板、坐盆盆面、坐盆簧架、滑轨内外板、滑轨上下支架等.本文选择座椅结构的钣金件为优化对象，钣金件的厚度作为设计变量.

由于座椅结构的钣金件比较多，为减少计算工作量，首先利用板件模态灵敏度分析的方法找到对座椅Y 向横摆模态影响较大的钣金件作为最终的优化对象，再用响应面模型替代复杂的、具有大量自由度的真实模型.经过灵敏度分析，最终确定了对该座椅进 行模态优化的12 个设计变量，见表4.

表4 座椅模态优化设计变量Tab.4 Design variables of modal optimization of the seat

2.3 拉丁超立方实验设计

对驾驶员座椅结构进行模态频率优化时，尺寸设计变量与座椅结构各系统响应间的对应关系需要通过构建响应面近似模型来拟合.拉丁超立方抽样可以用较少实验次数提供更多的信息，降低实验误差，其在非线性拟合方面具有优势.图4 为拉丁超立方采样示意图，其原理是在n 维空间中，将每一维坐标区间，k ∈[1，n ]均匀地等分为m 个区间，每个小区间记为，i ∈[1，m].随机选取m 个点，保证一个因子的每个水平只被研究一次，即构成n 维空间，样本数为m 的拉丁超立方设计[9].本文采用该抽样方法构建了座椅结构不同设计参数组合下的样本矩阵，得到样本模型231 个(表5)，表5 中Mi为样本序号i 时座椅结构总质量，fi为样本序号i 时座椅Y 向横摆模态频率.

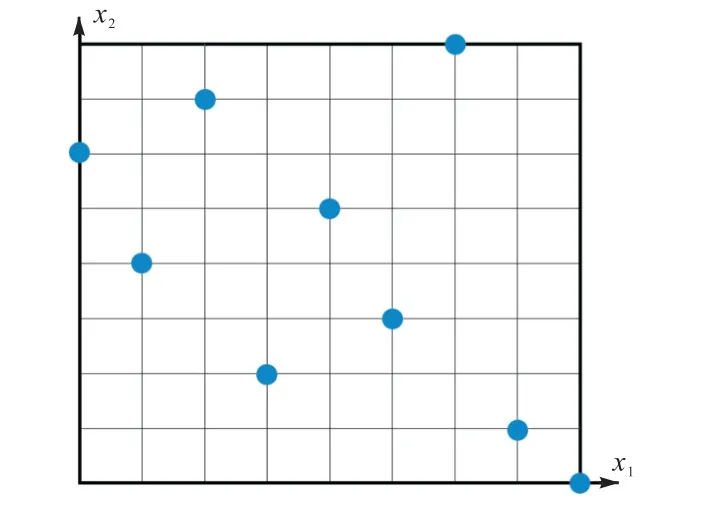
图4 拉丁超立方采样示意图Fig.4 Latin hypercube sampling diagram

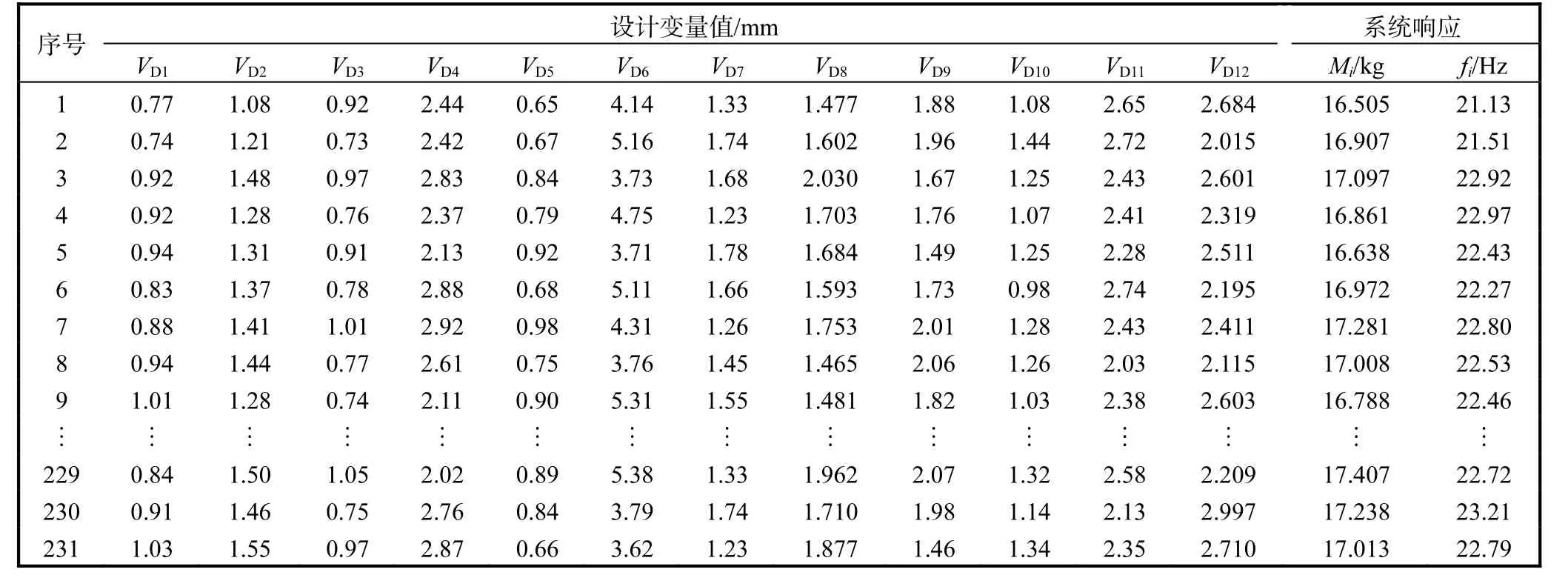
表5 驾驶员座椅结构实验设计结果Tab.5 Experimental design results of the driver seat structure

2.4 Kriging响应面近似模型的建立

Kriging 响应面近似模型是一种基于统计学的方法，该方法从优化变量的变异性和相关性出发，在设计空间内对变量进行最优、无偏估计，其在非线性响应数据建模方面也能具有较高的精度[10].输入变量和系统响应为对应关系的Kriging 模型可表示为

式中：Y (x) 为建立的Kriging 模型；f (x) 为设计空间的全局近似模型；δ (x) 为局部偏差，该偏差需要满足的统计特性如下：

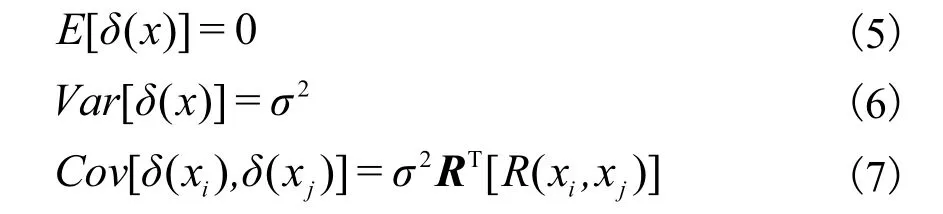
式中：E 为数学期望；Var 为方差；Cov 为协方差；RT为沿对角线对称的相关矩阵；为采样点xi和 xj之间的相关函数.

采用响应面近似模型进行优化时，须对模型精度进行检验.常用的检验指标有决定系数 R2、调整的决定系数和平均平方误差MSE，其表达式分别为

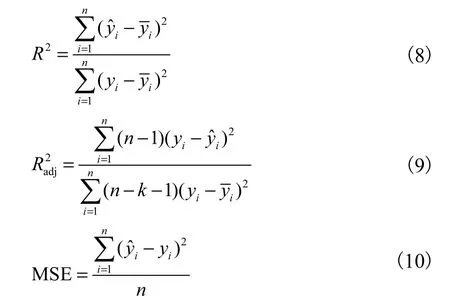
由定义可知，若 R2和越接近于1，说明近似替代模型拟合的精度越高；MSE 越小，说明模型的精确性越好[11].本文以 R2和MSE 为检验标准，经分析得到决定系数 R2＝0.999 8，MSE ＝1.01×10-17，说明本次拟合的Kriging 响应面近似模型精度较高，满足优化计算要求.

3 驾驶员座椅的模态优化

3.1 优化目标函数的建立

座椅结构的模态优化是在座椅总质量不增加的基础上进行的，已知座椅初始质量为16.998 kg.优化问题目标函数表达式为

式中：f 为座椅Y 向横摆模态频率；M 为驾驶员座椅总质量；VDi为设计变量；VDL和 VDU分别为各设计变量的上、下限.

3.2 基于遗传算法的优化计算与分析

遗传算法(genetic algorithm)是模仿生物进化理论而发展起来的一种自适应和全局搜索的优化方法，在优化中采取概率化的方式，能自动获取和指导优化的搜索空间，并能自动调整搜索的方向，以便于求出全局最优解[12].

运用遗传算法，对式(11)中的目标值f 基于所建立的座椅Kriging 近似模型进行全局寻优，迭代次数为30 次.得到座椅模态频率可行优化解集，即Pareto最优解集，各响应迭代过程如图5 所示.从解集中选取座椅整体质量减少且Y 向横摆模态频率提高，并满足目标要求的优化解作为最优方案.将优化方案中的设计变量值按照钣金件常用厚度进行修正，修正后的优化结果见表6.

图5 各响应迭代过程Fig.5 The iterative process of responses

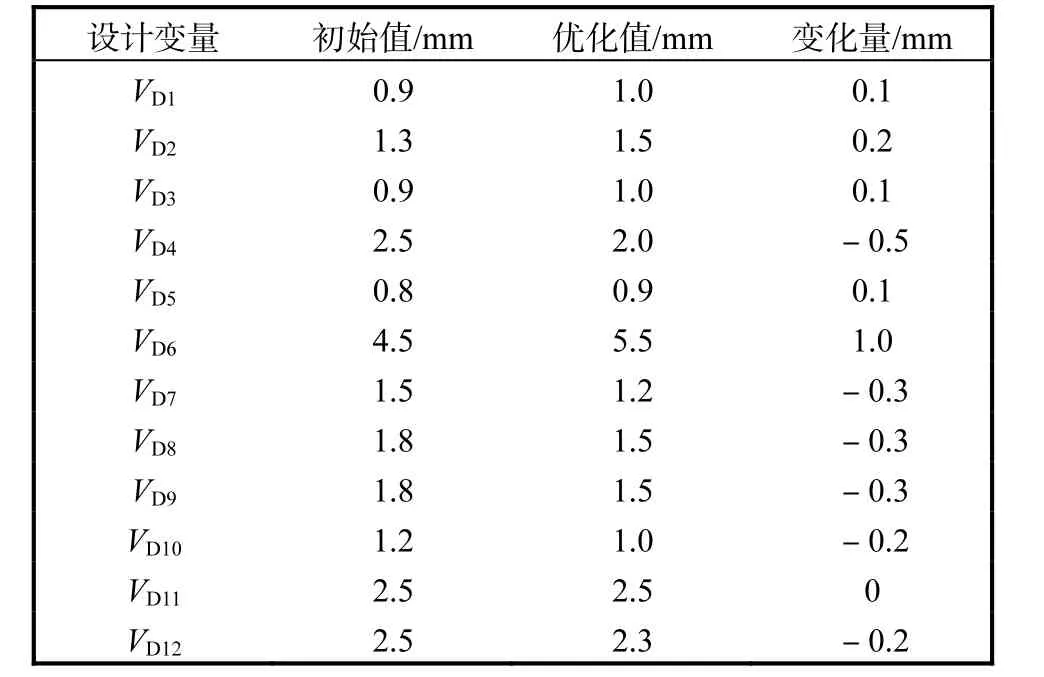
表6 座椅结构模态优化前后的尺寸Tab.6 Size of the seat structure before and after modal optimization

用优化后的设计变量值替换座椅模型的原厚度值，进行仿真计算后得到新的质量、模态频率等响应，并与优化前的座椅模型仿真结果进行对比，结果见表7.

表7 模态优化前后仿真结果对比Tab.7 Comparison of calculation results before and after modal optimization

4 结 论

本文建立了某轿车驾驶员座椅的有限元模型并进行模态分析，通过板件模态灵敏度识别的方法确定了对模态频率和质量影响较大的12 个设计变量.采用拉丁超立方抽样的实验设计，构建Kriging 响应面近似模型的方法，结合遗传算法对座椅结构的模态进行优化计算.优化后座椅的Y 向横摆模态频率由22.69 Hz 提高到24.60 Hz，达到了主机厂制定的目标值，同时座椅总质量减少了5.2%.从而实现了座椅模态优化的目的，验证了本文提出的基于响应面法的汽车座椅模态优化方法的有效性.