基于分形维数的风机表面损伤图像分割

石林立 徐锋 王攀

摘要：针对风力发电机表面损伤视觉检测中存在辨识率低、丢失率高和易受背景影响的问题，提出一种利用分形维数分割风力发电机表面损伤的方法。在传统差分计盒方法计算图像分形维数的基础上，利用图像分块处理的思想计算分形维数并统计各分形维数区间的数量，并选取分形维数分布曲线中的首个峰值作为分割阈值来实现自适应损伤分割。实验结果证明，改进差分盒维数法能够准确描述损伤并去除复杂环境下的背景，损伤图像分割的准确率达到88%，召回率达到89%，分割后的图像更加接近于标准自然损伤图像。

关键词：风机表面;分形维数;损伤分割;差分计盒维数;闽值

中图分类号：TM315 文献标识码：A

文章编号：1009-3044（2020）06-0191-04

1概述

由于传统的碳基能源在能源和环境方面的严重问题，可再生和清洁能源被认为是新一代的能源来源。由于能源的低成本和风能的灵活性，风能项目的开发成为能源获取的重点。风能作为一种可再生的新能源，近年来随着风能稳定性的提高和风电叶片成本的进一步降低，使我国风电业得以迅速发展。

风电叶片作为风力发电机组的主要部件，其需要在高空全天候不间断地运作，承担着主要的风力载荷嘲。风机叶片一般由玻璃纤维复合材料制成，因其制造工艺的复杂性，在成型过程中难免会出现缺陷。导致叶片的运转过程中就会出现开裂等情况，这些裂纹将在叶片运转过程中影响到整体风电叶片的结构安全问题。另外，风电叶片通常运作在偏远的野外，暴露在复杂多变的恶劣工作条件下，由于工作环境的恶劣性与工况的复杂多变性，在运行过程中叶片随着承受负荷的不断累加，微小的缺陷也会不断地扩大，逐步影响叶片的使用寿命。

为解决风机损伤所带来的一系列问题，国内外都对无损检测中表面损伤图像的分割进行了深入研究。在利用图像处理分形维数的技术中，提出了使用基于小尺度的分割方法、图像边缘特征提取的方法m和基于边缘梯度的检测法，但因为风力发电机自身环境的复杂性，造成目标图像具有复杂的背景、易受光照的影响，上述方法在目标分割时受背景干扰强，易误分割。风电叶片损伤的形成有其内在材料与外身环境因素，表面损伤虽然是随机和不规则的，但具有自相似性，在一定尺度范围内符合分形结构规律，所以为了使分割后的图像更加接近标准图像本文研究了图像分割问题。采用了一种基于分形和分形维数（FD）概念的技术。而分形主要反映图像表面特征，可以对不同纹理图像进行分割。但由于分形方法注重灰度信息，所以对损伤图像中的背景也考虑了主要细节，基于此提出针对差分计盒方法的一种改进算法，将采集的风电叶片损伤图像利用分形维数的方法将损伤提取出来，以提高风机表面损伤的检测精度。

2分形理论

分形是指具有复杂性和不规则性的事物，存在局部和整体以某种方式相似。分维是突破传统维数整数定义，将维数视为分数，定量的去描述客观事物的非规则程度。由1973年Man-delbrottgl在法兰西学院讲课时首次提出设想。

分形理论就是运用分形分维的数学工具，采用非线性的方式，客观分析描述复杂事实的真实属性和状态的一种手段。主要用于研究自然界中不规则复杂和复杂现象的一种科学理论和方法。

2.1分形维数

目前，数学家们已提出了拓扑维、容A维、自相似维、盒子维、信息维、相关维等多种分形维数。分形维数是分形特征中的复杂形体不规则性的量度，形象反映了复杂形体占有空间的有效性。

分形维数的计算有多种方法，例如，标尺法、盒子法旧、半方差法、随机游走法、频域法等。在计算图像分形维数方面的常用方法是盒子法和随机游走法，及频域法。其中盒子法最为经典，最著名的例子是测量英国海岸线，通过不断在海岸线图片上铺设更精细的网格，计算包含海岸线的网格正方形的数量来计算出海岸线的长度。

2.2差分盒维数算法

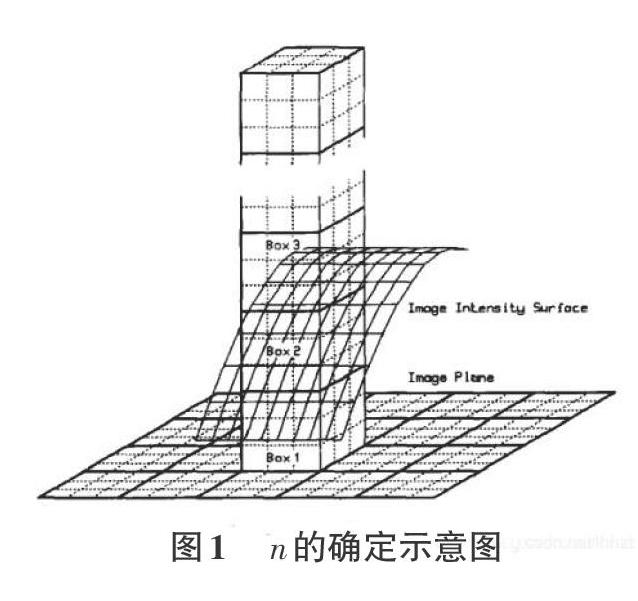
Mandelbrot认为分形的表面具有严格的自相似性。n维欧氏空间中的一个有界集合A，由Ⅳ，个独立的，互不覆蓋，缩小比例为r且与A相似的部分组成。有界集合A的分形维数（FD）D可从下式得到

3差分图像分割算法改进

原始盒维数法比较简单，但难以处理大数据量的图像。因此本文采用图像分块处理提高分形维数的精度。

输入.M×N矩阵A。

Stepl.填充A边缘像素值成大小为（M+2）×（N+2）的图像。

Step2.从大小为（M+2）×（N+2）图像中选取包含M×N的一个像素点并选取一个矩形领域，为图像中的一块区域。

Step3.在每块矩形领域中再次划分s×s的区域，s选取2¹、2²和2³，并计算不同尺度下的r，r=s/M。

Step4.在每个尺度r下，计算每个网格对应的n（i.j）=p-k+1，其中p和k分别是网格灰度最大值和灰度值最小值所在的盒子序号，然后再移动网格。

Step6.用最小二乘法拟合-log（r）和log（N）求其斜率，作为该区域下图像的分形维数D。

Step7.依行遍历A中的像素点，重复执行Step2～Step6，计算出每个矩形领域的分形维数D，最终得出每块局部的分形维数，并绘制各分形维数区间的数量分布曲线。

输出.分形维数与数量的分布曲线。

3.1改进差分盒维数与自动阈值结合

对图2风力发电机表面损伤的灰度图片进行分析：

在总灰度值为256，损伤邻域范围内灰度值相对未损伤领域范围内灰度值小的多。再用一系列尺寸大小为s×s×g的盒子去覆盖一个（x，y，f（x，y）（x，y，f）（x，y）的表面（其中f（x，y）为图像在（x，y）位置处的灰度值），造成在网格（i，j）中落最大灰度值为p的盒子和落最小灰度值为k的盒子之间的盒子数n（i，j）增多，由此也引发公式（3）中的N相应的变大。随着Ⅳ的变大，由公式（1）得D值就会相应的增加。相应地在未损伤的领域范围内，各点的像素在灰度值上差异不大，也造成因分别落最大灰度、最小灰度得P、K值相差不大而n（i，j）趋近为0，D值较小。基于此：选取统计分形维数分布曲线的第一个曲线峰值所对应的分形维数值作为阈值，来达到对损伤分割。

图3是图2原始图像中d的分形维数分布曲线，选取图示分割阈值就得到如图2所示d的分割阈值。用这种方法自适应得到不同损伤图片的分形维数分割阈值。

4实验结果与比较

4.1损伤检测对比

图2是从工业相机采集的小型风力发电机数据集中挑选了4幅具有典型性的原始图像，用于损伤图像视觉结果的比较。图4～图7是损伤图像分割的视觉对比图，展示了本文算法与传统的全局差分盒维数法、Otsu阈值法和canny法的实验结果对比情况。从图2原始图像可以看出损伤图像存在叶片表面出现裂缝、涂层老化以及由麻面导致产生的砂眼或坑洞，同时有由近景、远景、天空和建筑等构成的复杂背景。

前三种的分割结果是由传统的图像分割算法处理得到的，可以从视觉上很明显地看出canny法在处理风力发电机损伤图像上因为采用两种阈值来檢测强边缘和弱边缘使得远景的树木和建筑成为弱边缘而被描述出来，造成描述损伤图像过度。Otus阈值法分割出的图像是由目标和背景之间的方差为依据，所以图5中c、d因目标和背景相近而造成分割结果局部出现大块的黑色部分，丢失了大量的图像信息使图像出现失真。从图6中的全局差分盒维数法分割的结果相比于前两种方法在分割方面在一定程度上有了提高，但是对于局部图像分割不是很好，物体的边缘信息描述的不充分，于是出现在轮毂表面、叶片表面和塔架表面大区域的模糊形状，a目标叶片端部受到图像的复杂背景的影响，不能够准确的分割图像。本文提出的分割方法不仅能够对图2中a具有复杂环境背景的进行准确的分割得到目标，对分割有麻面、砂眼特征的图像干扰也较小。总体来说本文所提出的方法较好。

4.2改进差分盒维数实验结果

为了客观的反映各图像分割算法的准确度，同时对算法分割评估结果既要具有准确性又要具有全面性。因此，本文对分割前后像素点的变化引入准确率Pr、召回率Re的定义，来实现对损伤图像分类算法的性能评估。

通过对采集到的220张损伤图像进行了大量的性能测试得到表1和图8，在保证召回率为80%以上的基础上即能够描述大部分图像为前提下研究准确率才具有代表意义，再通过对比这四种算法的准确度就能够客观上得到各算法的优劣。

从表l可以得到在召回率在80%以上，前三种方法因为复杂环境背景而导致分割的准确率均在50%以下，而本文所研究的算法可以达到88.1%的准确率，F测度达到0.89，再一次验证了本文的研究算法的优越性。

如图8所示，得出各算法的P-R曲线，可以看出前三种的分割方法的P-R曲线均在本研究方法的P-R曲线以下。总体来说，本文在风机损伤图像的分割上具有很高的准确性和召回率。

5结束语

本文研究了对风力发电机损伤图像的改进差分盒维数进行计算，并将其应用到复杂环境下裂纹的分割。可以看出：改进的差分盒维数与自动阈值法相结合的方法，考虑了整体和局部的图像信息，能够更好地描述图像，在提高裂纹分割的精度的同时，有效降低局部丢失的错误;能够从复杂环境（图像表面具有复杂纹理、背景存在天空和树）中得到高质量的分割图像;实验对比发现复杂环境下微小的细节分割仍有待进一步提高。