基于核心素养的初中数学解题研究

王世强

解数学题时有何规律可循？解题时怎样分析思考才能找到解题思路？怎样从有限的“已知”（显性条件）出发挖掘更多的“可知”（隐性条件），进而顺理成章地走向“未知”结论？这是每一个与数学打交道的人都不自觉地去思考、求索的问题。

人们常说一千个人眼中就有一千个哈姆雷特，一千个人有一千种看待事物、分析问题的思想和方法，解题也是一样。笔者旨在抛开人的主观因素和个性化的思维特质，立足于《义务教育数学课程标准（2011版）》和数学学科核心素养等相关理论，从中汲取思想的营养，探寻数学解题的奥秘。

我们知道，高中阶段的数学核心素养包括数学抽象、逻辑推理、数学模型、直观想象、数学运算、数据分析六个方面。义务教育阶段学生的数学核心素养也离不开八个核心关键词：数感、符号意识、推理能力、模型思想、几何直观、空间想象、运算能力、数据分析。数学抽象主要表现为符号意识和数感，推理能力即逻辑推理，模型思想即数学模型，直观想象体现的就是几何直观和空间想象。这六大核心素养（八个核心关键词）既是培养学生的能力要素，又可以成为分析问题、解决问题时的思维方法和思维工具，对培养和提升学生的解题能力至关重要。

下面以哈尔滨市2019年中考数学第26题为例，谈一下基于核心素养的解题思路。

已知：MN为⊙O直径，OE为⊙O半径，AB、CH是两条弦，AB⊥OE于D，CH⊥MN于K，连接HN、HE，HE与MN交于P.（1）如图1，若AB与CH交于点F，求证：∠HFB=2∠EHN;（2）如图2，连接ME、OA，OA与ME交于Q，若OA⊥ME，∠EON=4∠CHN，求证：MP=AB;（3）如图3，在（2）的条件下，连接OC、BC、AH，OC与EH交于G，AH与MN交于R，连接RG，若HK：ME=2：3，BC=根號2，求RG的长.

1.利用“数学模型（模型思想）”全面把握条件和结论信息，进行初步分析思考。

从哲学角度来说，定义、概念等“数学知识模型”是思维的基本单位。对数学题目初步的分析思考就是建立在对题目中所有条件信息和结论信息与相对应“数学知识模型”紧密联结和深度联想的基础之上的，我们只有全面把握已知，深入理解与每一个已知相关联的所有知识点，明确命题的本质，才能为后继解题过程筑牢坚实的基础。

解题实操经验：借助对“信息点”的线性联想，进行“信息点”与“知识点”的对接，完成对数学知识模型的建构性揭示。

①MN为直径，OE为半径.由直径、半径模型联想到的知识点有直径和半径的定义和性质，还有直径所对的圆周角是直角.②AB⊥OE，CH⊥MN ，OA⊥ME.由圆中半径与弦垂直模型联想到的知识点有垂径定理.③∠HFB=2∠EHN，∠EON=4∠CHN.由圆中角模型联想到的知识点有圆周角和圆心角的性质.④MP=AB.由两条线段相等联想它们分别等于其他哪条线段.⑤HK：ME=2：3.由比的数学模型联想到引入参量，利用线段间数量关系尽可能多地表示其他线段.⑥求RG的长，根据“解题信息就近集中原则”联想RG所在的图形ΔORG，为解三角形模型做铺垫.

2.利用“直观想象（几何直观）”梳理基本图形，为挖掘隐性条件提供框架支撑。

综合题难想、难做，原因在于显性条件数量有限，而隐性条件却深藏不露。隐性条件是指题目中未明确表达而客观存在的条件。这些条件常常巧妙地隐没在题目和图形之中，极易被学生忽视。隐性条件具有藏得深、数量多，若明若暗、不易识别的特点，所以学生常常感到无处下手、思路受阻而使解题陷入困境。此时全面挖掘隐含条件，为解题打开入口就成为问题解决的关键。如何挖掘？分两步进行：第一步就是上面谈到的借助“数学知识模型”对显性条件进行初步浅层次直线性挖掘，第二步就是借助日常解题经验中归纳梳理出的基本图形（数学经验模型）及其中蕴含的边角数量关系进行深层次发散性挖掘。这是彰显解题功力的核心环节。

除了数学知识外，每一种代数、几何基本题型的解题方法和一般处理方式，及基本图形中的边角数量关系也可视为数学模型，即 “数学经验模型”。在解综合题过程中，借助“直观想象（几何直观）”对题目复杂图形进行自由而灵活的“数学经验模型”识别和拆解，进行思维方法的迁移和重组，都是有效的解题路径。

古往今来的数学家都十分重视直觉思维的作用。迪瓦多内说：“任何水平的数学教学的最终目的，无疑是使学生对他要处理的数学对象有一个可靠‘直觉。” 当下的教学过程，教师过度强调证明过程的严格化、程序化，用僵硬的逻辑外壳掩盖住直觉的光环，学生也片面地把解题成功归于逻辑的功劳，而丧失了“可靠的直觉”，这恰恰是我们教育的失败。加强直觉思维练习是提升解题能力的有效途径。

解题实操经验：借助题中“信息点”间的组合式联想全面挖掘“数学经验模型”。

① AB⊥OE，CH⊥MN两个垂直组合式联想发现“对角互补四边形模型”（图4），进而与条件∠HFB产生思维联结，等量推导发现∠HFB=∠EON，进而第一问可证;②由∠EON=4∠CHN和第一问的结论∠HFB=2∠EHN组合式联想得到“圆周角、圆心角模型”（图5、6），发现∠PHC=∠CHN和∠HPN=∠HNP，挖掘出“等腰三角形HPN三线合一模型”和“八字双等腰三角形模型MEP和HPN”（图7），进而得到MP=ME;③由OA⊥ME和之前的垂直条件AB⊥OE组合式联想发现“共叠合角∠AOE全等双等腰三角形模型OME和OAB”（图8），进而等量代换推出第二问结论MP=AB。

3.利用数学抽象（数感）发散式联想，深度挖掘隐性条件，提升学生合情推理能力。

数感是学习数学必须培养和提升的一种重要的数学素养，它能将数与实际背景联系起来，它使学生看到的“数学经验模型”中的边角之间有了特殊的数量关系，从而自然引入特殊数据深入表达这种特殊的数量关系，解题时这是一种主动、自觉或自动化地理解和运用数及运算的基本能力。

解题实操经验：借助“数学经验模型”中蕴藏的特殊数据深刻表达边角数量关系。

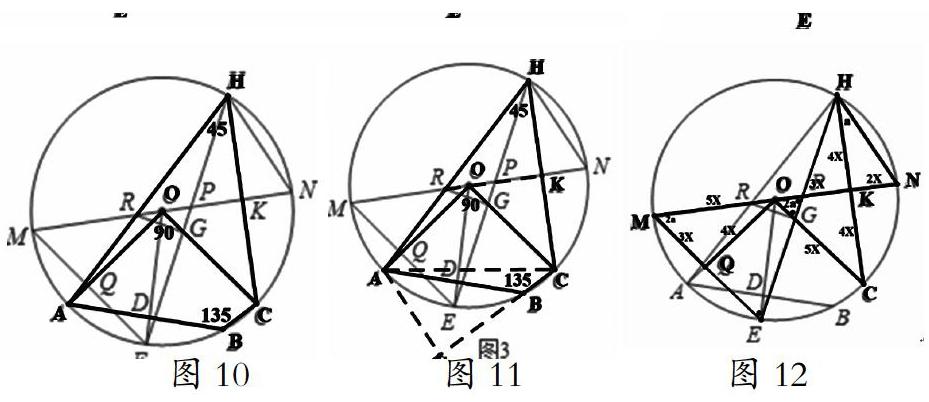
图9中蕴藏着邻补角的角分线互相垂直基本图形，联想到特殊数据90度;进而联想到图10中蕴藏着互补的两个圆周角45度和135度;依次联想到图11中的特殊数据，做135度的邻补角45度。即延长CB，过点A做BC的垂线AS，构等腰直角三角形ABS，还有图11中的特殊图形等腰直角三角形RHK，得到RK=HK;由图12中∠CON=2∠CHN=2∠CHP，tan∠COK=4/3，联想到特殊数据1/2=tan∠CHN=tan∠CHP。这些边角间的特殊数据为后续挖掘新一轮的隐性条件搭建了沟通的桥梁。

4.利用数学抽象（符号意识）发散式联想，深度挖掘隐性条件，提升学生合情推理能力。

挖掘隐性条件进行解题是一种极具创造性的思维活动。隐性条件是数学题目中的固有条件，它或以逻辑演化螺旋递进的方式内隐于显性条件之中，或以“数学经验模型”为骨架得以依附。从某种意义上讲，数学也是语言的艺术，在问题解决的过程中，往往需要借助文字语言、图形语言和符号语言来对思维路径进行刻画。特别是利用符号语言（符号意识）对显性条件进行逻辑推理等价变式，对“数学经验模型”中的边、角元素进行数量关系的全面深度刻画和多元符号化表达，往往可以让隐性条件在不经意间自然而然地显露出来。

解题实操经验：借助对题中“数学经验模型”边角数量关系的符号化表达，全面挖掘隐性条件。

数学是一门科学，数学解题是一门艺术。通过数学解题教学和研究，让学生亲身去体会最原初的思维模式和最本真的思维路径，感悟思维的无为发散与策略收敛，在真实的情境中培养解题能力，我们能够培养出更多的艺术家，思维演绎的艺术家，而不是打造解题的工人和解题的机器。那种跳进题海盲目刷题的教学方式是对学生未来的幸福人生极大不负责任的行为，需要我们严厉的批判和无情的摒弃。实践告诉我们，在《课程标准》的理念指引下，持续高扬“学科核心素养”的旗帜，用理论的航标指引解题教学的航程， 学生必将会感受到豁然开朗、水到渠成的解题境界，也必然會体会到数学学习的美妙和数学解题的美妙。

编辑/傅    戈