基于改进PSO的局部阴影下光伏阵列MPPT控制
2020-04-22王豪王宏华
王豪,王宏华
(河海大学 能源与电气学院,江苏 南京 210098)
0 引言
光伏发电具有分布广泛、无污染、方便等优点,成为当今的研究热点。其中,光伏系统的最大功率点跟踪(maximum power point tracking,MPPT)控制,是提高其发电效率的重要措施之一。然而在局部阴影下,光伏阵列的P-V曲线呈现多峰值现象,传统的MPPT算法(如爬山法、电导增量法等)难以追踪到最大功率点。针对该问题,文献[1] 利用局部阴影下光伏阵列最大功率点电流与短路电流之间近似的比例关系,提出一种三步骤全局MPPT算法,其结构简单,但动态调整过慢。文献[2]针对传统MPPT算法进行改进,提出了差分进化(DE)算法与变步长扰动观察法结合的复合控制算法,但其依赖于光伏组件参数并且控制复杂。文献[3]采用斐波那契(Fibonacci)搜索法,但是该方法不能对任意情况进行MPPT,实用性不强。
粒子群优化算法(particle swarm optimization, PSO)作为全局寻优算法,非常适用于多峰值光伏系统的MPPT。文献[4-6] 采用粒子群算法实现多峰MPPT控制,能对任意阴影情况进行最大功率点跟踪,但其收敛速度慢。文献[7-8] 对传统粒子群算法进行改进,分别提出了惯性权重对数递减粒子群和变异粒子群算法,可显著提高收敛速度,但其仍易陷入局部最优。基于此,本文采用改进的粒子群优化算法实现光伏阵列局部阴影下MPPT控制,针对传统PSO容易陷入局部最优解,即“早熟”缺陷,引入自适应调节的惯性权重和学习因子进行进一步优化,提高算法的收敛速度。通过仿真验证改进后的算法在不同阴影条件下,能够快速且准确地跟踪最大功率点,提高了光伏阵列输出效率,具有良好的实用价值。
1 光伏阵列的多峰值特性分析
单块光伏电池可用图1的等效电路来表示。
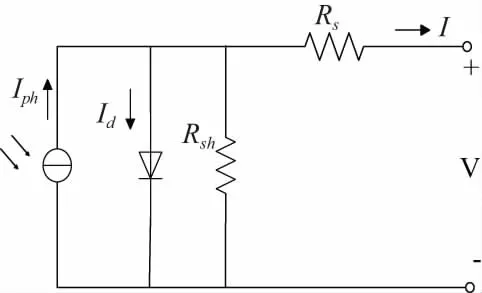
图1 等效电路图
本文采用一种适合工程应用的近似仿真模型[9-11],根据电池厂商提供的标准环境下相关参数和对不同环境下电池性能参数的修正得到如下公式:
I=Isc[1-C1(eU/(C2Uoc)-1)]
(1)
C1=(1-Im/Isc)e-Um/(C2Uoc)
(2)
C2=(Um/Uoc-1)[ln(1-Im/Isc)]
(3)
式中:U、I为光伏电池的输出电压和电流;Isc为短路电流;Uoc为开路电压;Im和Um分别为最大功率点所对应的电流和电压。
光伏阵列由多个单体光伏电池串并联而成,其输出特性可视作单体电池输出特性的叠加。由文献[1] 可知,局部阴影下并联的光伏组件可相对独立工作,其P-V曲线仍呈单峰特性;然而,处于局部阴影下串联的光伏组件,其P-V曲线将呈现多峰值特性。图2为3个光伏电池串联组成的阵列,每个光伏电池并联一个旁路二极管,防止其工作在反向电压。
本文仿真采用的太阳能电池型号为MG-P50,厂家给出的性能参数为:Pm=50W,Uoc=21.5V,Um=18.4V,Isc=2.95A,Im=2.72A。参考温度是25℃,参考光照为1000W/m2。在局部阴影下,3块光伏电池的光照强度将不再相同。假设此时PV1的光照强度为1000W/m2,PV2为800W/m2,PV3为600W/m2,在该种情况下阵列输出的P-V、I-V曲线如图3所示。此时,阵列的开路电压Uoc_array=64.5V。当阵列输出电流i
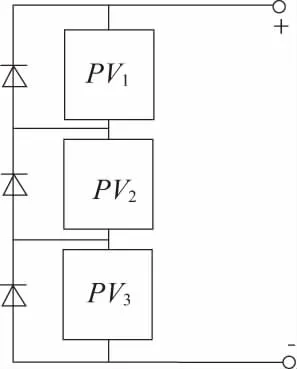
图2 3块光伏电池串联
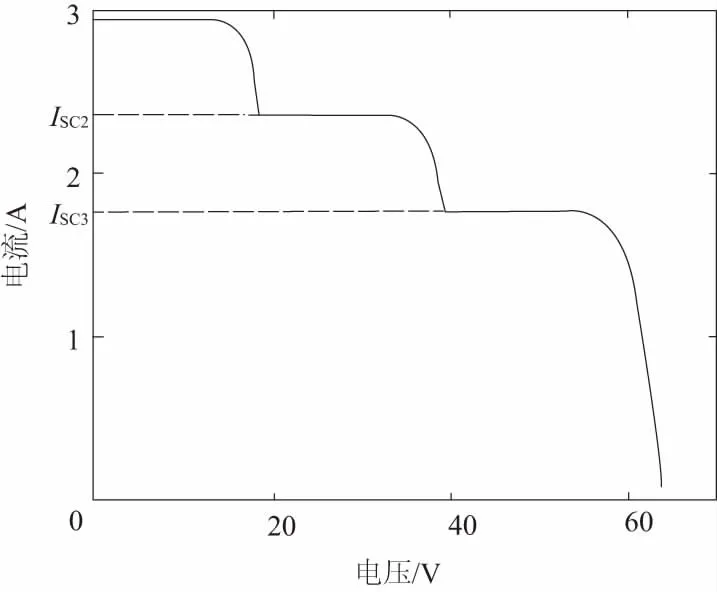
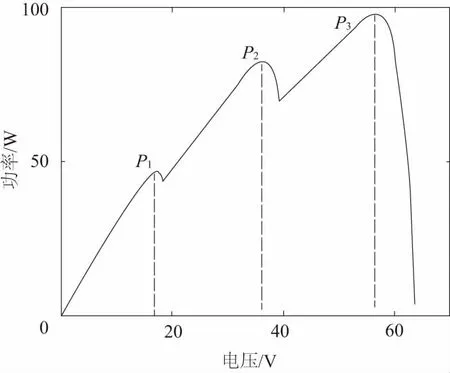
图3 局部阴影下I-V, P-V曲线
通过上述分析,可推广到一般情况,当串联阵列中由n块电池组件受到局部阴影影响,光照条件不一致时,其I-V曲线会出现n级阶梯,P-V曲线将呈现出n个峰值点。文献[6] 指出,当粒子群优化算法的粒子数目和粒子初始位置选取不当时,容易造成PSO算法陷入局部最优,导致无法跟踪到最大功率点。
2 改进PSO算法在最大功率跟踪中的实现
2.1 改进PSO算法
PSO算法作为一种全局搜索算法是多极值函数寻优的有效方法,其原理是初始化一群随机粒子(随机解),然后通过迭代找到最优解。每个粒子都具有由速度、位置和目标函数决定的适应度。在每一次迭代中,粒子通过跟踪两个极值来更新自己的位置和速度,一个为粒子自身到目前为止的最优解,简称为个体极值(Pbest);另一个是整个种群目前找到的最优解,即全局极值(Gbest)。种群中任意一个粒子的位置和速度更新方程如下式所示。
(4)
(5)
式中:i表示第i个粒子;k表示迭代次数;w为惯性系数;c1和c2为学习因子;r1、r2为[0,1] 上的随机数;x、v为粒子的位置和速度。
在PSO优化算法进行最大功率点跟踪过程中,惯性权重w和学习因子c1、c2的取值对算法的性能具有重要影响[10];w取值过大会难于得到精确解,反之,过小会导致陷入局部最优;同时,初期设置较大的c1和较小的c2可避免“早熟”,后期较小的c1和较大的c2可以加速收敛。因此,本文采用了一种自适应调节的方法,随着迭代次数k的增加更新学习因子c1和c2并按指数函数递减的惯性权重,其公式为:
(6)
(7)
w=wstarte-k/kmax
(8)
式中:kmax为最大迭代次数;c1start,c2start和c1end,c2end为起始和终止学习因子;wstrat为初始惯性权重。
2.2 改进PSO在MPPT中的应用
在光伏阵列最大功率点跟踪中,粒子群算法的适应度函数为测量阵列的输出功率。将光伏阵列的电压作为搜索变量,则粒子的位置代表光伏输出电压值,其速度即为电压增量。通过上文可知,PSO优化算法粒子数目和初始位置选择不当会导致跟踪失败。因此,粒子个数应大于等于极值点个数;同时,粒子应均匀分布在整个电压区间内,否则会陷入局部最优而导致跟踪失败。
由于在最大功率点附近反复多次迭代会产生长时间的波动,为了避免在最大功率点附近振荡并使系统快速稳定在最大功率点上,本文对PSO优化算法设计了终止策略。当各粒子间的最大电压差<0.5%Uarrray时,即认为找到最大功率点,停止迭代;并将此时所有粒子中对应功率最大粒子的值定义为Um,最大功率定义为Pm。
上述方法针对的仅仅是阴影情况固定的MPPT,而在实际情况下阴影和光照强度都会发生改变,最大功率也随之变化,所以应在算法中加入重启条件。定义功率变化量p为
(9)
式中Preal为在Um下光伏阵列的实际输出功率。当p大于设定阈值时,重启算法,重新寻找最大功率点,其流程图如图4所示。
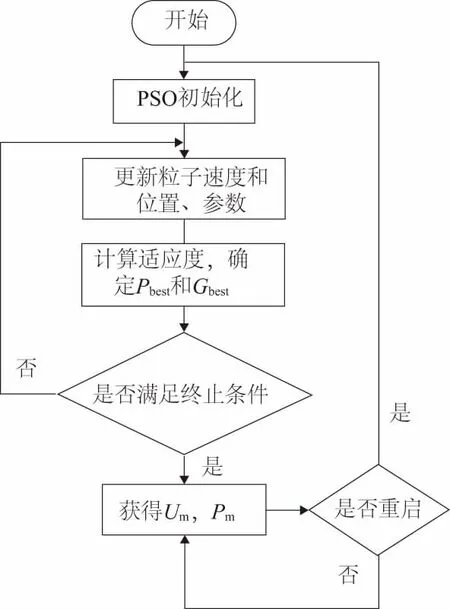
图4 改进PSO流程图
3 仿真分析
3.1 仿真模型
为验证改进PSO优化算法在MPPT控制中的正确性,本文在simulink中搭建了基于Boost电路的光伏最大功率跟踪系统[13],其系统框图如图5所示,其中光伏阵列由3块MG-P50型光伏电池板串联组成。Boost电路的仿真参数如下:光伏输入滤波电容C1=200F,直流母线电容C2=1000F,Boost升压电感L=5mH,负载R=80,开关频率为10kHz。
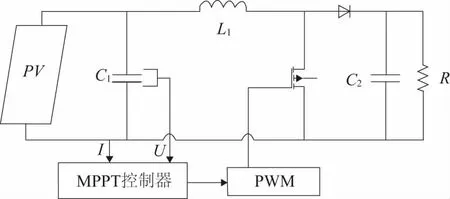
图5 最大功率跟踪系统
MPPT控制器模块中,控制过程为将改进PSO算法中粒子当前电压作为给定电压,光伏实际电压作为反馈,通过PID调节调制占空比D,最终实现MPPT。
3.2 仿真分析
仿真时采用3块光伏电池串联组成光伏阵列,并设计了两种阴影条件。阴影1条件下3块光伏电池的光照强度分别为:PV1=1000W/m2,PV2=800W/m2,PV3=600W/m2;阴影2时PV3的光照强度突变为200W/m2;两种阴影下的P-V曲线如图6所示。阴影1的最大功率和其对应的电压分别为Pm= 98.31W,Um=55.92V;阴影2的最大功率和其对应的电压分别为Pm= 82.56W,Um=36.34V。

图6 两种阴影下的P-V曲线
本文在仿真时,选取5个粒子,其初始位置均匀分布在电压区间内;初始惯性权重w=0.8;最大迭代次数为100。首先,在MATLAB中分别编写两种算法来验证算法的正确性,得到的适应度(即功率)曲线如图7所示。从图中可以看出,改进PSO算法在15代找到了最大功率; 而PSO算法陷入了局部最优,并经40次迭代才结束。
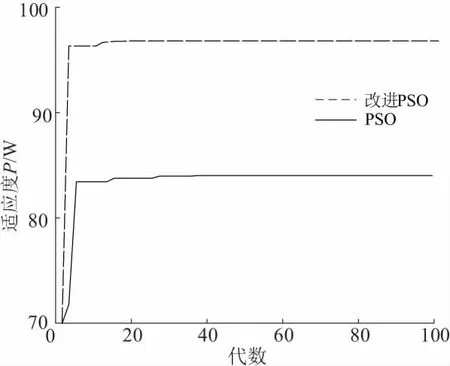
图7 适应度曲线
将MATLAB中的算法改写成S函数与Boost电路一同仿真,得到的功率和电压波形如图8和图9所示。PSO算法则经过1 s的搜寻找到了最大功率点,其在搜索过程中一度陷入了局部最优,最后成功跟踪到最大功率点;Pm=96W,其功率波动范围为95.6~96.4W,电压波动范围54.3~54.8V。
改进PSO在0.3s时追踪到了最大功率点Pm=97W,电压稳定值为56V,其电压和功率跟踪误差<1%;其功率波动范围在97.65~97.85W之间,电压波动范围在56~56.3V之间。
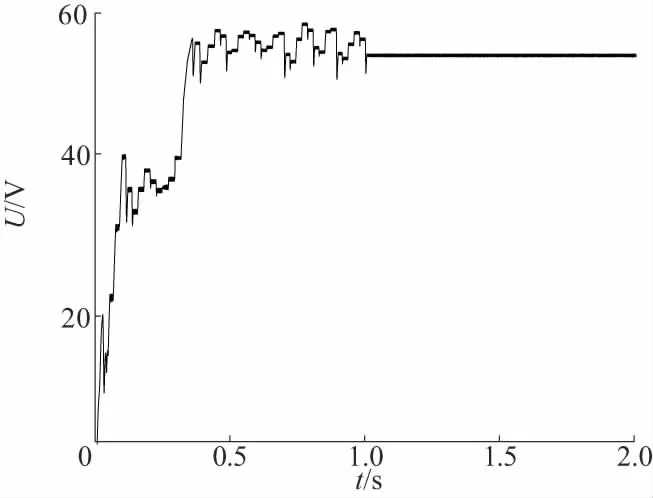
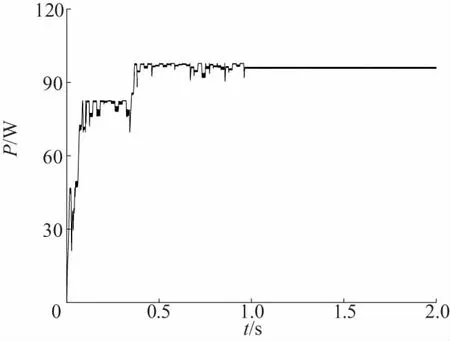
图8 阴影1下PSO的电压、功率跟踪结果
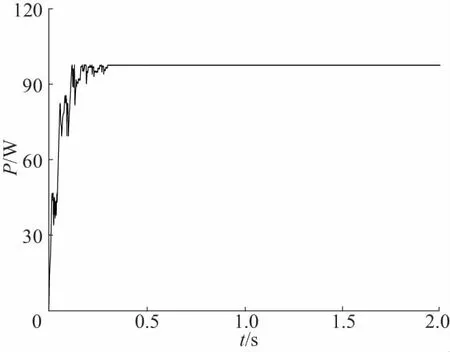
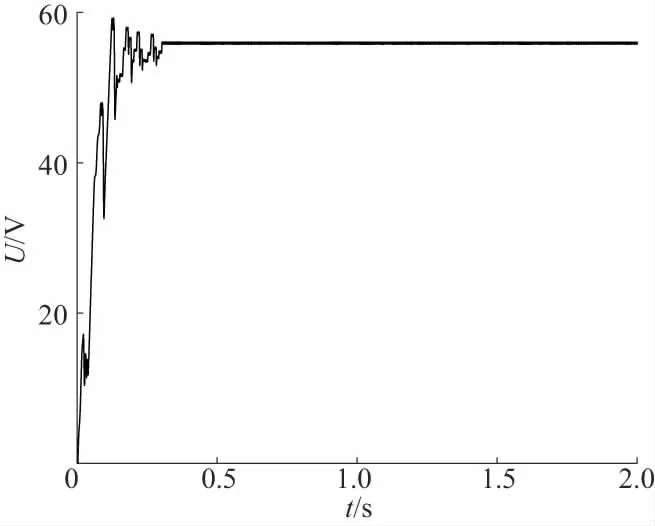
图9 阴影1下改进PSO的功率电压、跟踪结果
上述只是考虑了静态条件,在实际中阴影会发生突变,因此需要考虑在光照强度发生突变时算法的有效性。在1s时由阴影1突变为阴影2,采用改进PSO算法的MPPT仿真结果如图10所示。在由阴影1突变为阴影2的瞬间,电压并未改变但功率快速下降,此时重启了算法进行寻优,经过0.3s重新追踪到了新的最大功率点Pm=82.6W。
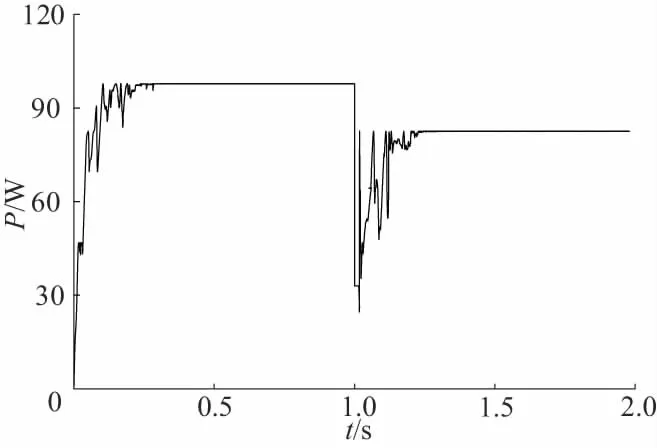
图10 阴影突变时仿真结果
4 结语
本文研究了一种改进的粒子群算法,并将其运用到局部阴影下光伏阵列的MPPT控制中。改进后的粒子群算法的惯性权重和学习因子能够自适应调节,克服粒子群算法易陷入局部最优的缺点,同时加快了收敛速度。通过仿真表明,经过改进的粒子群算法,在静态和动态环境下都能够实现MPPT,提高了光伏系统的发电效率。
