FSAE赛车四轮转向系统PID控制仿真
2020-04-22孙浩洋赵鹏飞马超戴伟恒
孙浩洋,赵鹏飞,马超,戴伟恒
(1. 南京理工大学 机械工程学院,江苏 南京 210096; 2. 北京理工大学 机电学院,北京 100000)
0 引言
随着汽车工业的不断发展,中国大学生方程式大赛对于FSAE方程式赛车的安全性、稳定性和性能的要求也不断提高。作为提高赛车操纵稳定性、主动安全性的四轮转向技术在这种背景下应运而生。研究发现,四轮转向系统不仅在低速工况下能减小转弯半径,提升车辆的灵活性,在高速工况下对车辆的操纵稳定性也有显著的作用[1]。四轮转向赛车的前轮和后轮同时作为主动转向轮,在转向过程中,不仅前轮转向,后轮也根据汽车的运动主动参与转向,对汽车侧向运动进行控制。四轮转向赛车的控制目标是实现汽车质心侧偏角为零[2],提高赛车在转弯时的操纵稳定性,减少赛车在比赛过程中滑出赛道的风险。
本文基于中国大学生方程式赛车四轮转向系统,通过前人得到的满足质心侧偏角为零的前后轮转角比例关系,建立服从阿卡曼转向的四轮转向模型。通过该模型求出后轮理论转角值,并作为实际情况下电机执行系统的输入值。然后建立电机模型,求出电机的传递函数,建立整体控制系统,并对其进行PID调节和仿真,分析结果,得出结论。最后得到一个完整的后轮转向控制系统的整体模型。
1 后轮转角理论值的求取
本文选用PID控制作为实际控制方法,输入为后轮转角的理论值,输出为后轮转角实际值,被控对象为电机的转动圈数。传感器分别为后轮左、右转角的传感器,传递函数将后轮转角的理论值转化为电机的运行时间。
1.1 左右后轮转角理论值的求取
由Sano分析[3]可得后轮转角的理论值为:
(1)
式中:∂为后轮理论转角 ;δ为前轮转角;lr为质心到后轴的距离;m为整车质量;L为轴距;lf为质心到前轴的距离;kf为两前轮的侧偏刚度之和;u为车速;kr为两后轮的侧偏刚度之和。
现建立4WS车辆转弯时的几何模型,由此求出后轴左右轮的转角。传统的前轮转向服从阿卡曼定理,使得4个轮胎做纯滚动运动。同理,为了使四轮转向汽车的4个轮胎同时做纯滚动,可以近似地认为四轮转向服从阿卡曼原理。因此可得4WS车辆转弯时的几何模型如图1所示[4]。
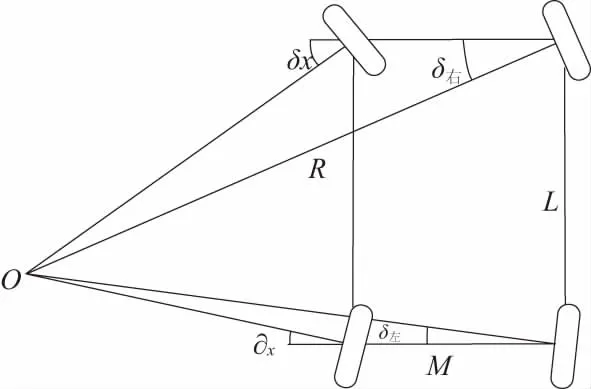
图1 4WS车辆转弯时的几何模型
图1中:M为后轮距;R为最小转弯半径;L为轴距。
由几何关系得:
(2)
(3)
即:
(4)
(5)
所以:
(6)
(7)
其中:∂左1为满足稳态侧偏角恒为0的左后轮转角值;∂右1为满足稳态侧偏角恒为0的右后轮转角值。
1.2 传递函数的求取
利用CATIA中的DMU空间运动分析模块,建立简化后的四轮转向模型。简化后的模型由后轮、转向节、转向横拉杆、转向节上下铰接点、直线滑块组成。采用直线滑块替代电机和丝杠,省略了将旋转运动转化为直线运动的过程,直接由滑块的直线运动驱动后轮转向模型,节省建模时间,且不影响分析结果。在DMU模块中设置后轮转角,以滑块的直线运动为驱动。因为滚珠丝杠的导程为2mm,即驱动滑块运动2mm电机转动一圈,设置滑块运动距离为-10mm~10mm,设置步长为0.1mm,得到相应的后轮转角度数,并将数据导出到Excel中,分析后轮转角和电机转动圈数的关系。
在Excel中由拟合数据得出后轮转角和电机转动圈数的函数关系为:
y=1.284 1x+0.097 9,
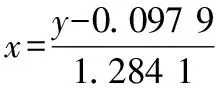
(8)
2 电机数学建模及PID控制策略推导
2.1 直流伺服电机数学模型推导
1) 电机转矩与电流关系
设电机转矩为T, 单位为N·m;电流为I,单位为A,其关系式:
T=Kt×I
(9)
其中Kt为力矩常数,单位为(N·m)/A。
2) 电机运动方程
设电机转矩为T,单位为N·m,负载转矩为Tf,单位为N·m,电机角速度为ω,单位为rad/s,电机角度(位置)为θ,单位为°(角度),有关系式:
(10)
其中J为转子转动惯量,单位为kg·m2。
3) 反电动势关系式
设电机反电动势为e,单位为V,电机角速度为ω,单位为rad/s,有关系式:
e=Ke×ω
(11)
其中Ke为反电动势系数,单位为(V·s)/rad。
4) 电机等效电路方程
依据伺服电机的工作原理,建立伺服电机的等效电路方程。设电机电压为U,单位为V, 电感为L, 单位为H,电阻为R, 单位为Ω,电流为I, 单位为A,反电动势为e,单位V, 有关系式:
(12)
2.2 电机模型的传递函数
将式(9)-式(12)进行拉氏变换,得到传递函数:
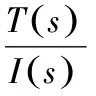
(13)
式中n为减速比。由于调节电流环时发现I(s)与U(s)传递函数含有反电动势,不便于观察稳态情况,故调节电流环时先采用不含有反电动势的I(s)与U(s)传递函数:
(14)
2.3 电机控制模型框图
根据式(13)、式(14)电机模型的传递函数,作出控制模型框图,如图2、图3所示。
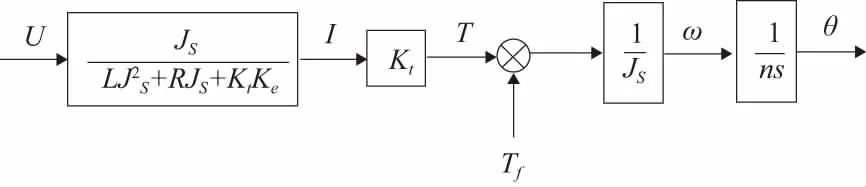
图2 电机控制模型框图(含反电动势)

图3 电机控制模型框图(不含反电动势)
2.4 电机系统传递函数
根据图2电机控制模型框图推导电机系统传递函数:

(15)
2.5 电机参数选取
根据电机参数表选取参数如下:
额定电压U=24V;
转动惯量J=0.285×10-4kg·m2;
线电阻R=0.19Ω;
线电感L=0.22mH;
力矩系数Kt=0.082(N·m)/A;
减速比n=10;
机电时间常数Tm=3.05ms;
速度限制=±3000r/min;
电流限制=±10A;
额定转矩T=0.637N·m;
反电动势系数Ke=5V/K·r·min-1=0.048 (V·s)/rad。
3 MATLAB/Simulink仿真
3.1 PID系数选择
1) 搭建Simulink模型
根据图3电机控制模型框图(不含反电动势)搭建Simulink模型,如图4所示。

图4 Simulink模型
图4中Kfs为速度反馈系数;Kfp为位置反馈系数,其数值由PID输出限幅及单位决定。
位置环PID输出限制=±10rad/s,速度环PID输出限制=±10A,电流环PID输出限制=±24V。


2) 电流环PID调节
先考虑不存在反电动势的情况,PID三项调节相互之间有影响,尝试多组数值后,综合考虑确定P=100,I=3500,D=0.08,波形如图5所示,波形无静差、无超调、调节时间大约为0.1s。
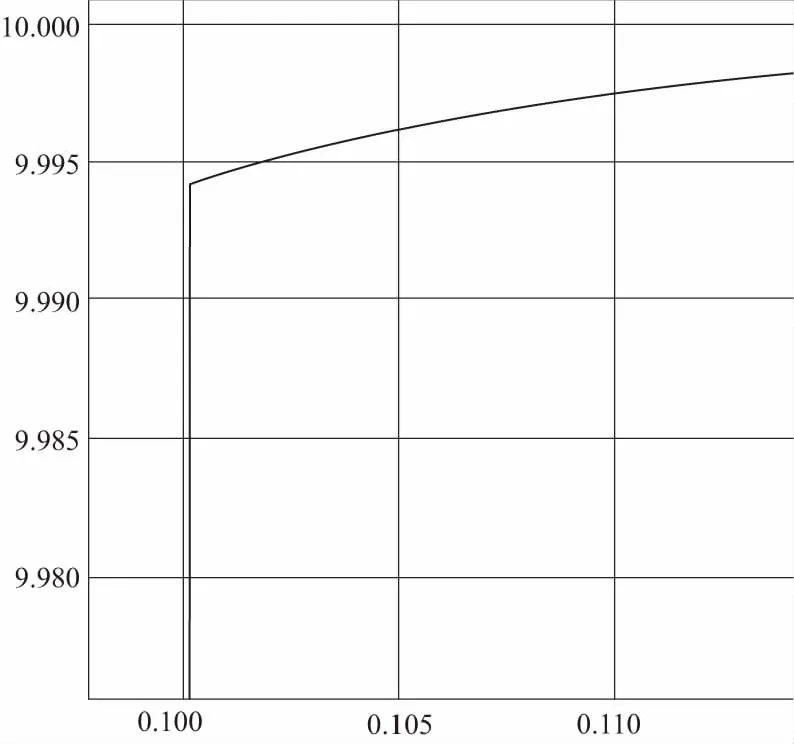
图5 电流环仿真图形
3) 速度环PID调节
经多次联合测试调节及综合考虑,确定P=600,I=0,D=0.05,输出波形如图6所示,无超调、无静差、调节时间<0.1s。
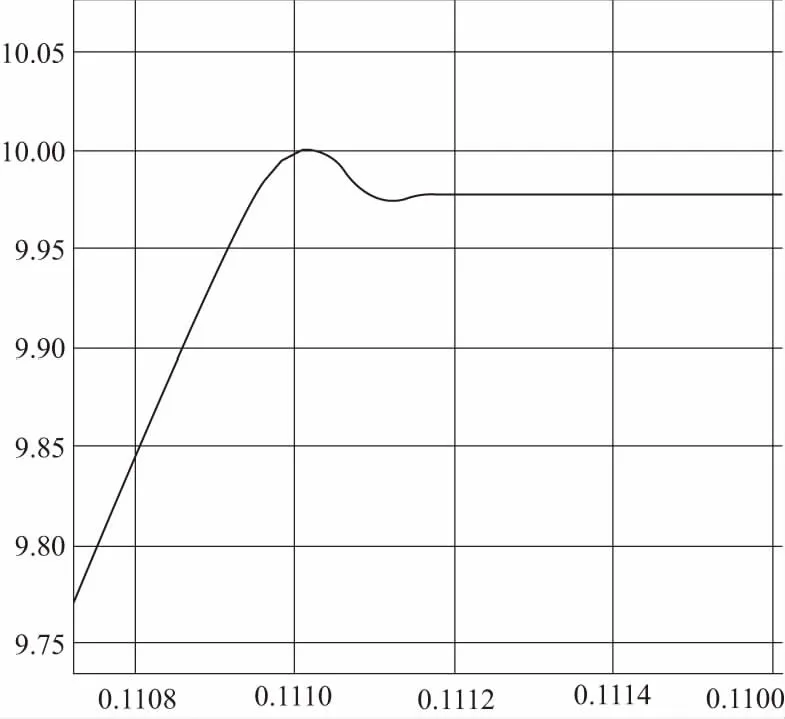
图6 速度环仿真模型
4) 位置环PID调节
经多次联合测试调节及综合考虑,确定P=5,I=0,D=0.0318,输出波形如图7所示,无超调、无静差、调节时间<0.06s。
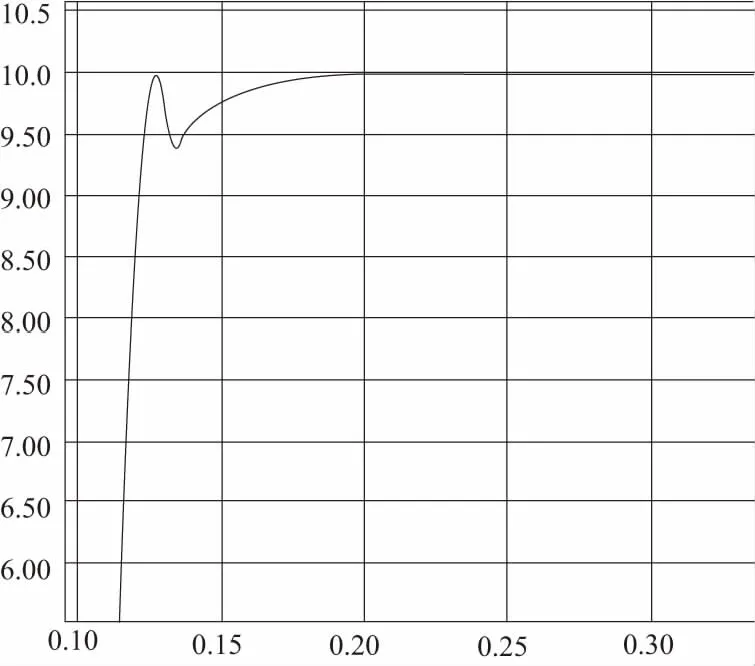
图7 位置环仿真模型
3.2 电机模型整体性能测试
1) 电机模型含有反电动势情况
在电流环PID调节时,为便于观察稳态情况,电机模型中没有加入反电动势。电机位置环、速度环、电流环PID均已完成调节,此时加入反电动势进行测试。其中:step为输入finalvalue=10,steptime=0.1的阶跃信号。
输出波形如图8所示,观察发现此时波形接近前面几图的波形,即反电动势几乎没有影响输出波形,其影响可忽略(因本刊为黑白印刷,如有疑问请咨询作者)。
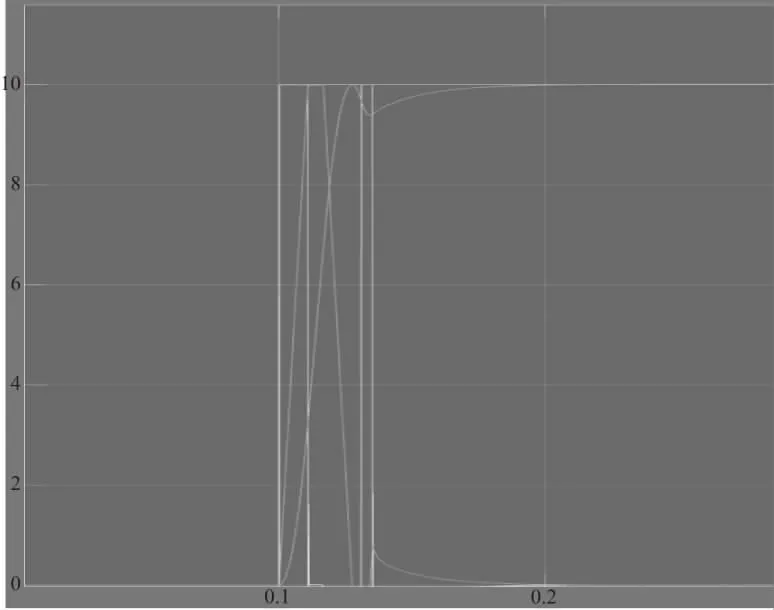
图8 含有反电动势的整体仿真波形图
2) 负载测试
在0.2s增加0.01N·m的负载,即图中Tf为输入finalvalue=0.01,steptime=0.2的阶跃信号。

图9 带负载的整体仿真波形图
输出波形如图9所示,观察0.2s加上负载时,电流短时间内立即增加,负载不变后,电流稳定。
3) 动态跟随测试
测试动态相应性能,参考位置输入正弦信号,将图中step换位Sine Wave,Amplitude=20,Frequency=10,观察输出波形如图10所示,实际位置曲线比参考位置曲线延时<0.001s。
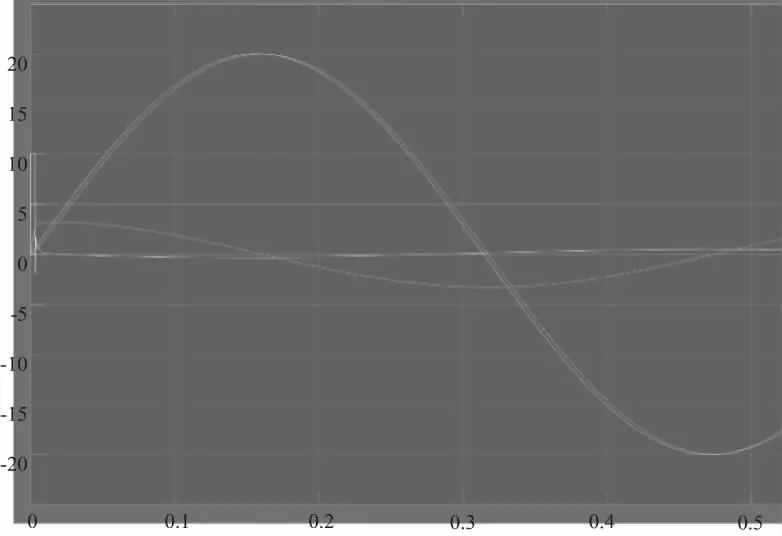
图10 动态跟随仿真波形图
4 结语
通过仿真分析发现,此控制策略能够有效地对后轮转角进行实际控制,控制无超调,滞后时间极短,因此可以作为一种控制策略进行实验分析和研究,而且此控制策略也是对大学生方程式赛车的一次大胆尝试。
