基于驾驶员生理负荷的高原公路转角值安全风险评价
2020-04-22王进州艾力斯木吐拉
王进州, 艾力·斯木吐拉
(新疆农业大学交通与物流工程学院,乌鲁木齐 830052)
道路安全是由人、车、路、环境四者的协调决定的,若四者不协调将增加交通风险,并且发生交通事故的主要是由人因素导致[1]。随着高原公路海拔的升高,压强减小,空气中氧气含量减小,驾驶环境越来越差,在道路线形和高原低氧环境的双重影响下,驾驶员心率变化显著[2-3]。潘晓东等[4]分析了在山区公路行驶过程中平曲线半径与驾驶员心率变化规律。乔建刚[5]分析了心率变化与驾驶员紧张度的关系,提出驾驶员紧张和恐惧心理状态下对应的心率增长率阈值分别为30%和40%。李岩岩等[6]研究了高原公路驾驶员β频段脑电波随海拔与道路线形组合值的变化规律。张娟等[7]研究了心率增长率随着上下坡的平曲线半径的变化规律,并给出合理取值范围。夏可等[3]研究了心率变化在高原低氧环境和弯道的双重影响下,随着平曲线所处海拔越高、半径越小,驾驶员心理紧张度变化越明显。李鑫磊[8]在软件仿真的基础上,通过重点对驾驶员方向控制的研究,建立综合仿真模型,并进行了直角转弯试验,通过对方向盘转角等指标的分析验证了仿真结果的合理性。Godley等[9]对车道宽度的研究发现较窄车道容易导致驾驶负荷的增加。Ronen等[10]通过对直线段行车过程中的心率变异率研究,发现在直线段行车时驾驶员更容易放松警惕。Spacek[11]研究发现在弯道上行车,不同驾驶员的车辆轨迹保持行为是不同的。但很少有学者研究在道路线形设计的转角值大小对驾驶员生理负荷变化的影响。故选取K作为驾驶员生理负荷的评价指标,分析平曲线转角与K的变化规律,以期为高原公路线形宽容性设计提供理论依据。
1 驾驶试验
1.1 试验段道路简介
行车试验路段选取国道314线,二级公路,起点为奥依塔格一桥,终点为苏巴士六、七桥,全程73 km。该路段的最低点高程约3 000 m,最高点高程约4 030 m。双向两车道,无护栏,无中央分隔带,车流较少,其他车辆的影响较小,路基宽度为12 m和8.5 m。该路段包含约80个转角值,可以较好地反映出驾驶员心生理随着道路线形转角值和海拔的变化规律。
1.2 试验人员及试验车辆
本试验选取3名无高原公路驾驶经验的驾驶员和1名经常在高原公路行车的驾驶员,4名驾驶员年龄在23~56岁不等;试验车辆为中型运动型实用汽车(sport utility vehicle, SUV)。
1.3 试验设备及数据获取
采用biofeedback 2000 X-pert 型生物反馈仪测取驾驶员行车过程中心率变化、脉搏血容等生理数据;采样率为200 Hz[12];用全球定位系统(global positioning system, GPS)记录车辆行驶的实时位置。
1.4 天气及驾驶员健康状况
本次试验在夏季进行,行车试验当天天气晴朗、微风。4名驾驶员身体健康状况良好,测试前一天睡眠质量良好,无较大情绪波动。
2 评价指标的选取
2.1 驾驶负荷评价指标的选取
2.1.1 心率增长率
心率增长率是业界公认的可以表征人体生理状态的评价指标,是某一段时间内的心率变化率;心率会受个体差异影响,大小不一,但心率增长率可以反映心率的变化幅度[13]。在行车过程中驾驶员面对外界环境、道路线形的变化显示出不同的变化幅度,通过变化幅度来判断驾驶员的生理变化。将心率数据通过式(1)转化为心率增长率。
N=100(n2-n1)/n1
(1)
式(1)中:N为驾驶员心率增长率,%;n1为各驾驶员静态平均心率,次/min;n2为各驾驶员动态平均心率,次/min。
2.1.2 脉搏血容 (BVP)
脉搏血容是反应驾驶员心跳强度的评价指标,当心脏收缩时,体表的毛细血管充盈,此时其透光率增加;当心脏舒张时,体表毛细血管处于收缩状态,透光性能降低,它反映的是驾驶员心搏力量的大小[14]。
2.1.3 驾驶员生理负荷(K)
在高原公路行车过程中,驾驶员生理心理指标同时发生变化,各指标侧重点不同,心率增长率表征心率变化的快慢,BVP表征驾驶员心跳的强度,通过MATLAB编程给心率增长率和BVP分配权重,得到K,K可以更全面地表征驾驶员生理负荷变化。
2.2 道路平曲线转角值
平曲线转角值是平面曲线切线旋转的角度;平曲线转角值与曲线长度、缓和曲线长度和半径均有密切联系;驾驶员在高原公路上行车时,随着平曲线转角值的增加,在通过曲线段时方向盘转动幅度会不断增加,并且需要保持的时间也会增加,所以选择道路平曲线转角值作为道路线形评价指标。道路转角与曲线长度、缓和曲线长度、平曲线半径的关系见式(2)。
α=180(L-Ls)/Rπ
(2)
式(2)中:α为平曲线转角值,(°);L为曲线长度,m;Ls为缓和曲线长度,m;R为曲线半径,m。
3 数据处理及分析
本试验仪器数据采集的频率为200 Hz,通过取200个数据的平均值合并为1个数据/s;取前10 min数据的平均值作为驾驶员静态数据(n1),(通过MATLAB短时傅里叶变换FFT)变换对数据进行降噪处理,将动态数据中误差较大的数据剔除,通过MATLAB数据编程对心率增长率和BVP进行权重分配,心率增长率分配系数为0.578 8,BVP分配系数为0.421 2,得到驾驶员生理负荷K,见式(3),进一步分析转角与K得关系。部分数据见表1。
K=0.578 8N+0.421 2B
(3)
式(3)中:K为驾驶员生理负荷值;B为BVP值,μV。
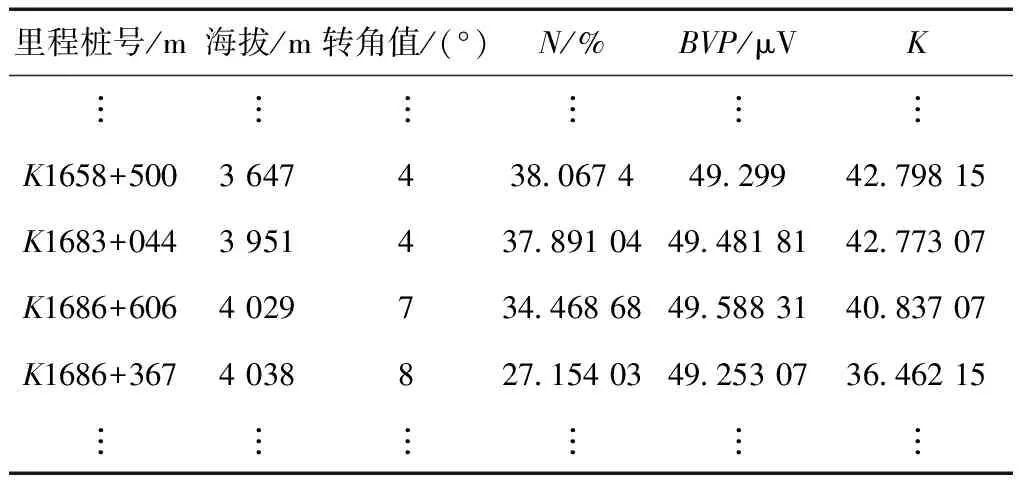
表1 部分转角值分析数据Table 1 Partial corner value analysis data
4 转角值对驾驶负荷的影响分析
4.1 偏相关性分析
利用SPSS软件对数据进行偏向关分析,控制海拔因素,分别对心率增长率、BVP、K与转角的偏相关分析,由表2可以明显看到,驾驶员在高原公路上行驶时,控制海拔因素的影响条件下,心率增长率和BVP与转角的相关系数分别为-0.492和-0.517,说明相关性显著,经过MATLAB分配给两个指标权重后的K相关系数为-0.503。
4.2 转角值单因素影响下驾驶员心理生理变化关系分析
4.2.1 心率增长率与转角的关系
利用SPSS建立平曲线转角值与心率增长率的关系模型,见式(4)。
N=-2.211lnα+37.126
(4)
式(4)中:α为转角,(°)。相关系数为-0.492,相关性显著,R2=0.469,拟合度较好;适用范围:海拔3 000~4 030 m。
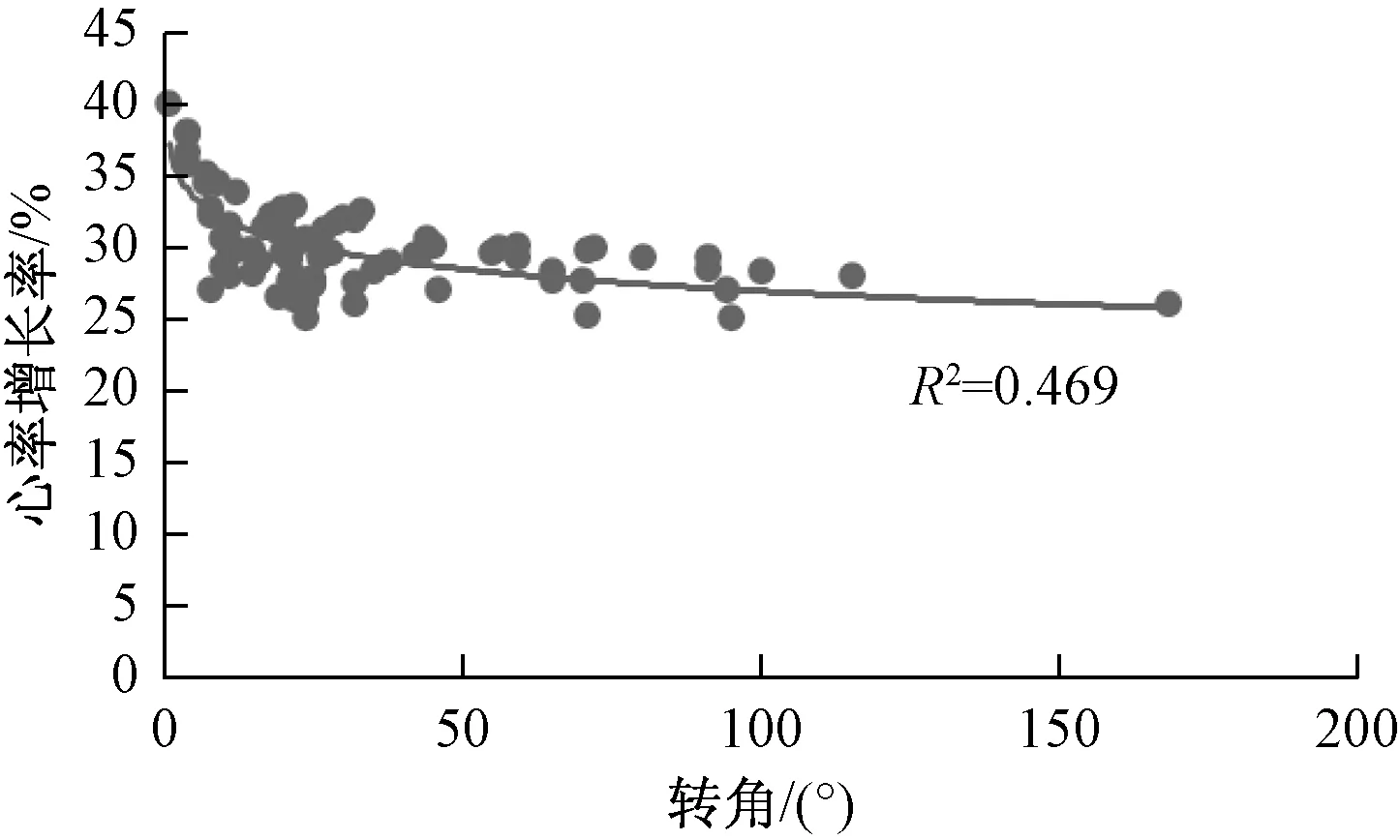
图1 心率增长率与转角关系Fig.1 The relationship between heart rate growth rate and corner
4.2.2BVP与转角的关系
图2为高原公路上行车时BVP与转角的曲线关系图,在海拔3 000~4 030 m内,转角0°~168°
内,BVP在49.6~48.8内。BVP随着转角值的增大而减小,转角值在0°~10°内,BVP较高,心跳强度较大,不利于行车安全,且随转角值的增加快速减小,在转角值增加到10°以上时BVP增加越来越慢。
利用SPSS建立平曲线转角值与BVP的关系模型,见式(5)。
1906年5月31日该委员会发表了一份17页的初步报告。他们的主报告,《州地震调查委员会报告,第一卷》,由Lawson编辑并于1908年出版。该报告包括对断层作用的地质和形态的大量描述、振动强度的详细报告,以及包括40幅超大尺寸图和对折纸的令人印象深刻的地图集。第二卷,由Henry Fielding Reid编辑并于1910年出版,主要描述此地震的地震学和机制方面。在本文后面的叙述中,将 《州地震调查委员会报告》(两卷:Ⅰ卷,Lawson,1908,和Ⅱ卷,Reid,1910;共643页)统称委员会报告,适时标出相应的卷号。今天该报告仍可通过购买或在线获得(见参考文献)。
B=49.474α-0.002
(5)
相关系数为-0.517,相关性显著,R2=0.350 4,拟合度较好;适用范围:海拔3 000~4 030 m。
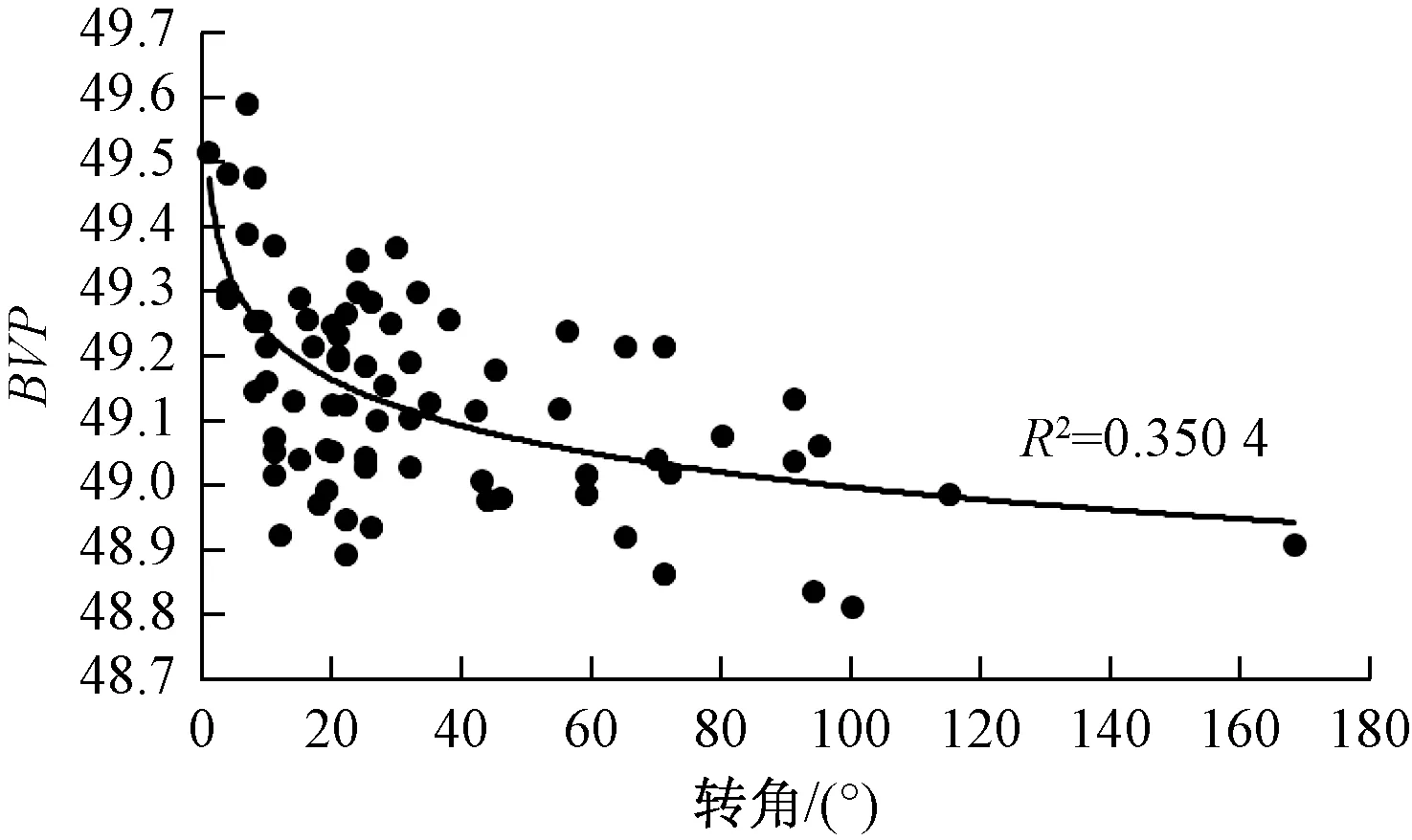
图2 BVP与转角关系Fig.2 Relationship between BVP and corner
4.2.3K值与转角值的关系
图3为高原公路上行车时K与转角的曲线关系图,在海拔3 000~4 030 m内,转角0°~168°内,K在35~44内。K随转角的增加而减小,当转角在0°~10°时,K较高,说明此时驾驶员生理负荷较高,不利于行车安全。
利用SPSS建立平曲线转角值与K的关系模型,见式(6)。
K=-1.324lnα+42.327
(6)

表2 在控制海拔因素下转角值与驾驶员生理负荷的偏相关分析Table 2 Analysis of the partial correlation between the corner value and the driver’s physiological load under the control of altitude factors
相关系数为-0.503,相关性显著,R2=0.482 8,拟合度较好;适用范围:海拔3 000~4 030 m。

图3 K值与转角值关系Fig.3 Relationship between K value and corner value
4.3 转角值和海拔的双重因素影响下驾驶员驾驶负荷变化关系分析
通过以上分析得出,相比于心率增长率和BVP单一指标来说,驾驶员生理负荷K与转角的关系表现出明显的相关性和拟合度,故本节重点分析在转角值和海拔的双重因素影响下驾驶员生理负荷K值的变化规律,鉴于夏可等[3]、李岩岩等[12]已经充分研究了驾驶员心理生理指标与海拔的关系,故不再赘述。利用MATLAB软件建立转角值、海拔和K的三维图,见图4。由图4可以明显看出,在转角值和海拔的双重影响下,K的变化更加显著。
利用SPSS建立平曲线转角、海拔和K的关系模型,见式(7)。
K=42.336+4.822×10-19exp(H/100)-1.338lnα
(7)
R2=0.484,拟合度较好;适用范围:海拔3 000~4 030 m。
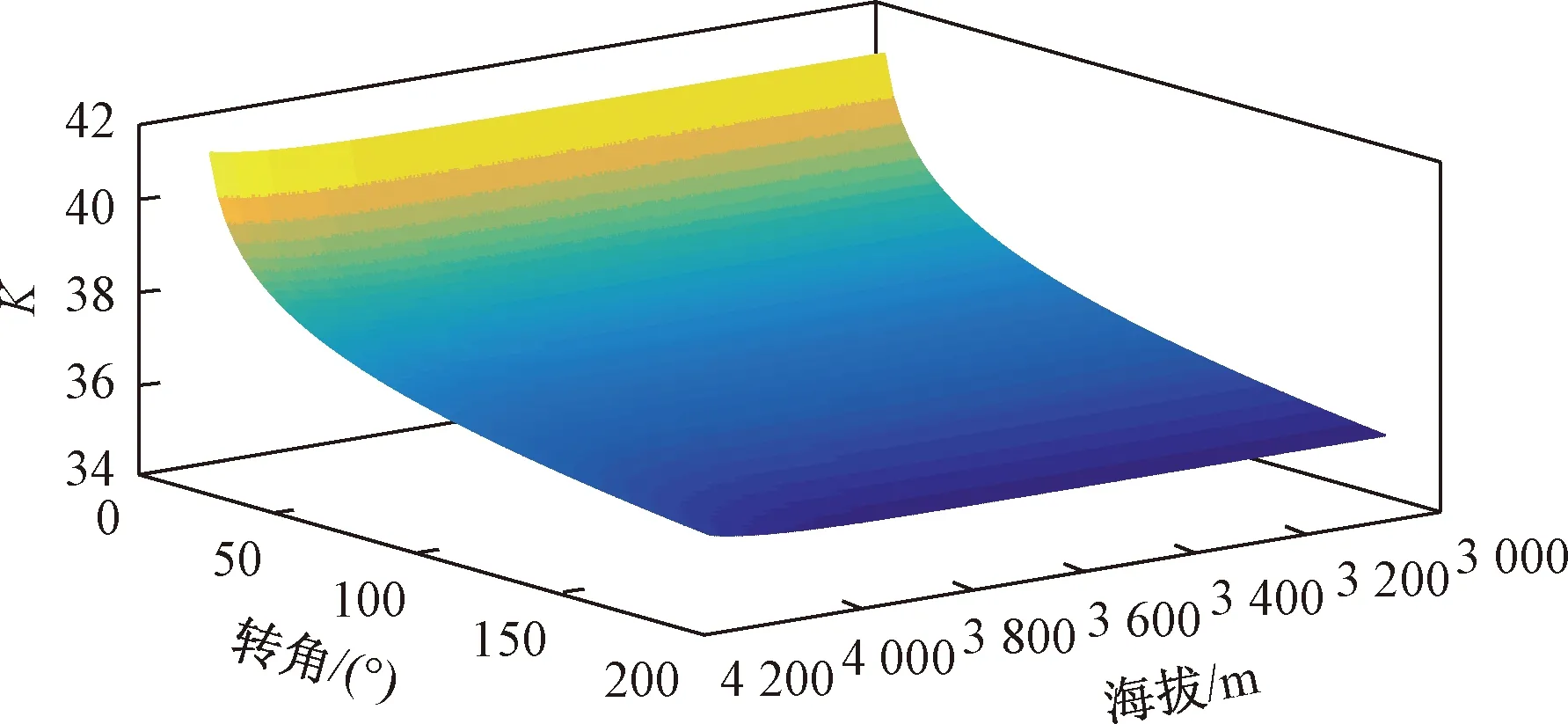
图4 转角值和海拔与K值的关系Fig.4 Relationship between the angle value and altitude and K value
5 结论
通过对高原公路道路平曲线转角值与驾驶员生理负荷关系的分析,得出以下结论。
(1)道路平曲线转角值对驾驶员心率增长率、BVP及K的影响显著,相关性显著。
(2)高原公路行车过程中,驾驶员心率增长率和脉搏血容随转角的增加而减小,且减小趋势由快到慢。
(3)高原公路行车过程中,转角值在0°~10°内,K较高,驾驶员生理负荷较高,不利于行车安全。
(4)从转角值和海拔与驾驶员生理负荷K的三维关系模型中发现,在海拔与转角值的双重影响下,随着转角越小,海拔越高,K越大,驾驶员生理负荷越高,交通风险越高。
