基于滑移网格方法的井下涡轮水动力性能仿真

2020-04-22李方韬薛启龙刘宝林张宗湖

科学技术与工程 2020年7期

李方韬, 薛启龙, 刘宝林, 王晋, 张宗湖

(中国地质大学(北京)工程技术学院，国土资源部深部地质钻探技术重点实验室，北京 100083)

叶片部件具有十分广泛的应用范围，其常见于风力机、水轮机、航空发动机等[1-4]。叶片部件在钻井工程也有重要应用，常作为井下动力装置被应用于涡轮发电机和涡轮钻具等[5-6]。井下涡轮发电机是常见的井下供电电源之一[7]。井下涡轮发电机作为轴流叶轮，通过井下不断循环的钻井液冲击使涡轮旋转，同时磁耦合器的磁耦合作用带动永磁发电机发电，从而实现为井下仪器连续供电的功能[8]。涡轮钻具也属于典型的叶片式轴流机械，其借助于叶片与流体介质之间的相互作用而工作，基于动量矩原理实现水力能量与机械能量的转换，最后由涡轮转轴输出转速和扭矩[9]。

随着计算流体力学(computational fluid dynamics, CFD)理论与数值求解方法的不断拓展和革新，CFD方法已经称为井下涡轮性能研究的重要手段[10-13]。Satti等[14]应用计算流体力学(CFD)来预测单级井下涡轮转子性能特性并通过与实验数据的对比，验证了模型在预测性能特性方面的可靠性。赵洪波等[15]通过CFD分析了涡轮钻具叶片型线对涡轮钻具的影响；沈玉琴[16]利用CFD方法对井下涡轮发电机的导轮和涡轮结构进行了优化；张晓东等[8]通过CFD流场分析，基于 BP 神经网络和 Fmincon 函数与遗传算法结合的方法对叶片进行了优化分析；Amini等[17]针对在石油工业中使用的正泥浆脉冲遥测(PMPT)系统中为交流发电机提供动力的涡轮系统，建立了模拟井下钻井环境的实验风洞，通过CFD分析验证了风洞实验数据。

涡轮运动是一个动态过程，涡轮在流体作用下被动受力旋转，涡轮的转速与流量、涡轮结构参数、涡轮所受外界负载等因素有关。目前针对井下涡轮的动态研究未见相关报道。因此，采用CFD方法探究井下涡轮的动态水动力性能。

1 涡轮设计与理论分析

涡轮模型如图1所示，叶片采用NACA66翼型[8]，该翼型具有良好的流动性能。基于某垂直钻井工具，井下涡轮设计为直叶片形式，其基本参数如表1所示。

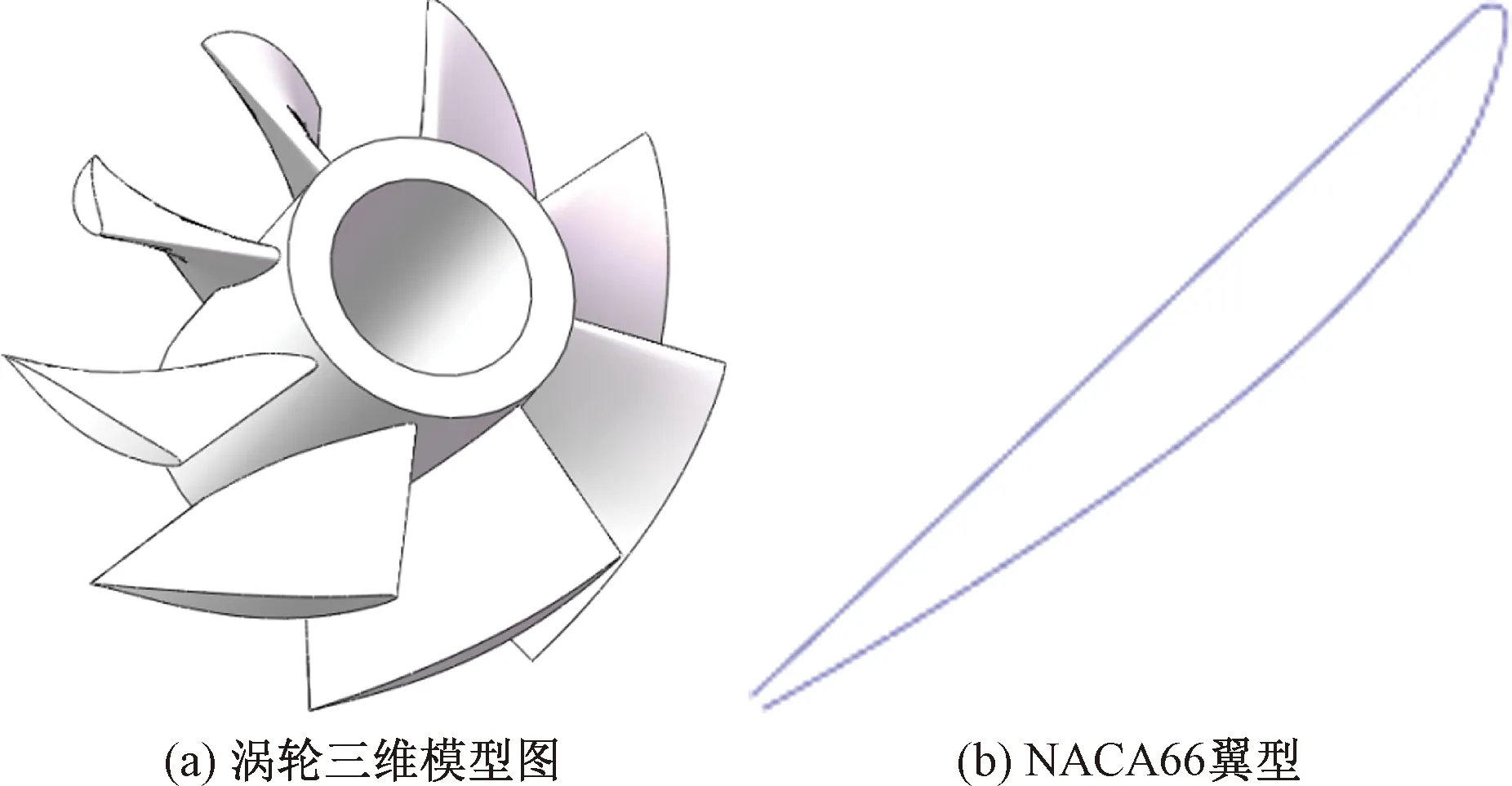
图1 井下涡轮设计Fig.1 Downhole turbine design

表1 井下涡轮基本参数Table 1 Basic parameters of downhole turbine

无论是涡轮发电机还是涡轮钻具中的涡轮定子，都通过转轴向外输出力矩及功率，涡轮承受外界的给予的负载。当涡轮由静止启动时，流体冲击产生的力矩和外界负载必须满足式(1)关系：

Tim>Tf

(1)

式(1)中：Tim为涡轮所受水力冲击力矩；Tf为外界负载。

涡轮转动方程为

(2)

式(2)中：Jy为总的转动惯量；∑My为涡轮所受总的外力矩，包括外界负载和流体作用产生的力矩。

2 仿真参数设置

2.1 仿真模型与网格划分

采用Fluent软件对涡轮进行仿真。仿真采用全三维流道模型，网格划分采用结构网格和非结构网格相结合的办法，如图2所示。对网格无关性进行验证后[18]，最终采用网格如图2(b)所示。

图2 仿真模型与网格划分Fig.2 Simulation model and mesh generation

基于滑移网格方法对涡轮进行动态仿真分析，为使仿真结果更为准确和收敛性更好，采用先稳态计算后瞬态计算的方法。

2.2 湍流模型

仿真模型选取较为成熟的k-εrealizable模型，其湍动能和耗散率输运方程为

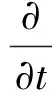
(3)

式(3)中，ρ为流体密度；k为湍流动能；ε为湍动耗散率；σk、σε为湍流动能k和湍动耗散率ε对应的普朗特数,σk=1.0，σε=1.2；xi、xj为位置坐标分量；ui速度坐标分量；v为分子运动黏性系数；Gk为平均速度梯度引起的湍流动能k的产生项；Gb是由浮力导致的湍动能产生项；YM为可压缩湍流脉动对总耗散率的影响；μt为湍流黏性系数；C1=1.44，C2=1.9。

为了更好地模拟近壁面流动，网格划分时，需要生成边界层，边界层第一层网格高度由式(4)决定[19-20]：

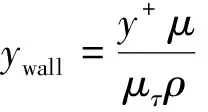
(4)

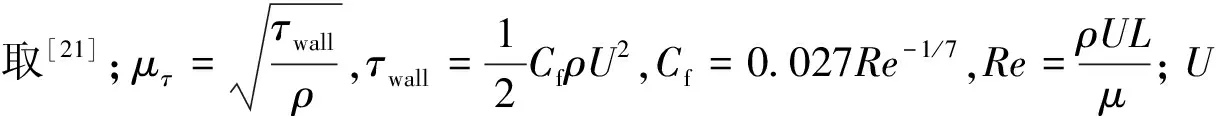
2.3 参数设置

在钻具尺寸结构一定的情形下，涡轮的基本尺寸也就被确定下来。涡轮叶片采NACA66翼型，故外界的负载、叶片安装角、流量、叶片数量是影响涡轮水动力性能的主要因素。在保持其他因素不变的情形下，外界负载分别设定为0、 2、 4、 6、 8 N·m，叶片安装角度分别为15°、 30°、 45°、 60°、 75°，入口流量分别设定为600、1 200、 1 800、 2 400、3 000 L/min，叶片数量设定为4、 8、12、 16、20，探究不同条件下，涡轮的动态水动力性能。

Fluent求解选用simple算法，采用二阶迎风格式进行离散，Pressure discretization采用presto格式。运用UDF(user defined function)控制滑移网格对网格进行动态调整。滑移网格根据涡轮的位置进行更新。涡轮角速度增量可由式(5)表示：

(5)

对涡轮运动过程中受流体作用产生的力矩、角速度、冲击力、角位移进行监测，得到不同条件下，涡轮的受力及运动规律，并对其结果加以分析。

3 结果与讨论

涡轮转速稳定时的涡轮应力云图和流线图，如图3所示。由叶片的应力分布知，涡轮上方的流体压力大，涡轮在叶片上部承受较大的压力，涡轮流体域下方形成旋流。常规的涡轮机构如风轮机、水轮机等常以叶素-动量定理对涡轮的受力进行分析，在分析中通常忽略掉流体冲击导致的动量变化，即忽视掉冲击力。然而相关研究者指出[22]，当涡轮尺寸变小时，涡轮因流体冲击受到的力不能忽视。故涡轮受力由三部分组成：冲击力、压差阻力、摩擦阻力。其中冲击力由流体动量改变造成，而压差阻力则由叶片前后压差产生，而摩擦阻力则由流体的黏性产生。涡轮是否转动取决于流体作用于涡轮的力矩是否大于外界的负载。流体产生的力矩小于外界的负载时当涡轮静止不动；当流体产生的力矩大于外界的负载时，涡轮开始运动。下文将分析外界的负载、叶片安装角、流量、叶片数量四个因素对涡轮的运动及受力产生的影响进行分析。

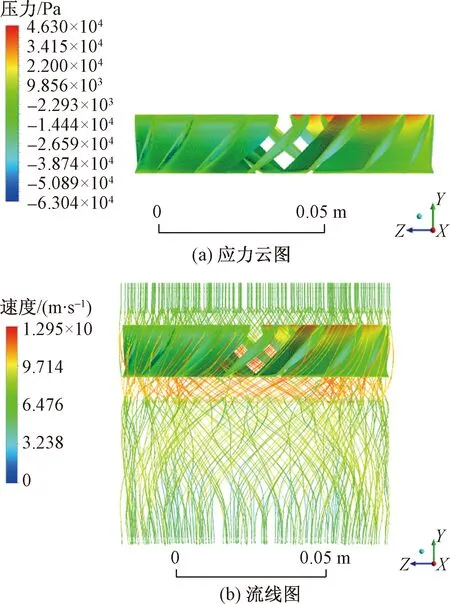
图3 涡轮转速稳定时，涡轮应力云图和流线图Fig.3 Turbine stress contour and streamline diagram when turbine speed being stable

3.1 启动特性

将涡轮静止不动时所受力矩及冲击力称为启动力矩和初始冲击力。涡轮静止时的受力决定着涡轮能否克服负载发生运动。不同因素对涡轮启动力矩和初始冲击力的影响如图4所示。对图4中曲线进行非线性拟合。如图4(a)所示，在保持涡轮结构设计不变及流体参数不变的条件下，涡轮所受外界负载的改变不会影响涡轮静止时的启动力矩和初始冲击力，拟合曲线为直线，其值为约7 N·m。

图4 不同因素对涡轮的启动力矩和初始冲击力的影响Fig.4 Effect of different factors on the starting torque and initial impact force of the turbine

如图4(b)所示，拟合结果表明，安装角的变化与启动力矩及初始冲击力呈四次关系，随着安装角的增加，涡轮启动时所受冲击力矩及初始冲击力有增大的趋势。涡轮叶片安装角度增加时，导致流体速度与叶片的攻角发生变化，进一步导致流体冲击涡轮导致的动量变化及叶片绕流流场变化，从而导致涡轮的启动力矩和初始冲击力发生变化。

流量的增加即意味着入口流速的增加，对不同流量情况下得到的启动力矩和初始冲击力进行拟合，发现入口流速和涡轮的启动力矩和冲击力呈二次关系，如图4(c)所示；随着流量的增加即入口流速的增加，涡轮所受扭矩增加且增幅增大，而冲击力的绝对值随流速增加，增幅增大。

如图4(d)所示，同样对不同叶片数量情形下得到的启动力矩与初始冲击力进行拟合，发现叶片数量与启动力矩近似呈二次关系，而与冲击力的大小呈线性关系。

3.2 运动过程

现就涡轮的运动过程进行整体分析。外界负载、叶片安装角、流量、叶片数量对涡轮运动过程所受外力矩、冲击力、角速度的影响如图5～图7所示。涡轮的负载较大时，流体作用于涡轮的力矩无法克服外界负载，涡轮静止不动，角速度始终为零，冲击力及力矩保持不变。当流体产生的力矩大于负载时，涡轮由静止开始运动，涡轮的角速度变化与涡轮所受冲击力矩直接相关。

涡轮由静止启动并开始转动时，其角速度不断增加，导致流体作用于涡轮叶片的攻角发生变化，这一方面导致叶片绕流流场变化，叶片所受阻力及升力在竖直方向的投影发生变化；另一方面导致流体冲击涡轮叶片时的动量改变，最终涡轮所受冲击力及水力力矩随角速度不断变化。当流体产生的力矩刚好克服外界负载时，涡轮所受总的外力矩为零，涡轮速度不再变化，流场趋于稳定，涡轮的角速度、冲击力矩、冲击力稳定。

3.2.1 涡轮角速度变化

外界负载、叶片安装角、流量和叶片数量对涡轮角速度的影响如图5所示。不同条件下，涡轮转速随时间的变化规律相同，涡轮转速随时间不断增加，最终转速恒定。随着涡轮外界负载的增大，涡轮稳定转速小，稳定时间越长；当外界负载为8 N·m时，外界负载大于涡轮的启动力矩，故涡轮停止不动。涡轮的安装角越大，涡轮稳定转速越大，稳定时间越长；入口流量越大，涡轮稳定转速越大，稳定时间越短。但入口流量的增加导致钻井液对涡轮的冲蚀强度增加，最终导致涡轮使用寿命的减小。叶片数量越多，涡轮稳定转速越高，稳定时间越短。叶片数目的增多会影响流体的分流，叶片越密集，流体流场越稳定[16]，但高叶片数导致转速增高，涡轮上下的压差增大，不利于钻井液流动。

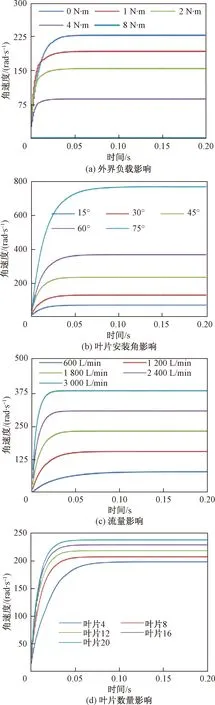
图5 不同因素对涡轮的角速度影响Fig.5 Effects of different factors on turbine angular velocity

3.2.2 涡轮冲击力变化

流量、外界负载、叶片安装角、叶片数量对涡轮冲击力的影响如图6所示。涡轮所受冲击力随时间的变化趋势相同，均先增加后稳定。涡轮冲击力变化与涡轮转速变化息息相关。涡轮转速增加时，冲击力变小，涡轮转速稳定时，流场稳定，冲击力不变。随着流量、外界负载、叶片安装角、叶片数量的增加，冲击力稳定时的值均减小。当涡轮的外界负载为8 N·m时，涡轮的冲击力不变，这是因为涡轮的启动力矩小于涡轮的外界负载，涡轮稳定不转的缘故。

图6 不同因素对涡轮的冲击力影响Fig.6 Effects of different factors on turbine impact force

3.2.3 涡轮力矩变化

不同流量、外界负载、叶片安装角、叶片数量条件下，涡轮所受力矩随时间的变化趋势相同，均先随时间不断减小直至趋于稳定，如图7所示。在不同外界负载的条件下，涡轮稳定时流体产生的力矩等于其受到的外界负载，涡轮所受外界的合力矩为零。不同安装角、流量、叶片数目均为无负载工况，涡轮稳定时流体产生的力矩始终为零。当涡轮的外界负载为8 N·m时，涡轮稳定不转，涡轮所受力矩随时间不发生变化。