考虑应力敏感和压裂液影响的页岩气井动态产能评价方法

刘建仪, 何汶亭, 廖鑫怡

(西南石油大学石油与天然气工程学院，成都 610500)

在页岩气藏中，页岩气以游离状态储集在基质和裂缝孔隙中，同时以吸附状态吸附在有机质等表面。吸附态页岩气占据气藏的比例可达40%以上，是页岩气藏的重要赋存方式[1-2]。Hartman等[3]在研究页岩气藏时，认为吸附态页岩气占据了气藏储量的绝大部分并且对产能的影响巨大；周登洪等[4]从地质物性和开发方面研究了影响页岩气藏产能的各种因素，认为页岩气藏中吸附气的含量构成了气藏产量的重要部分并且是影响页岩气产能大小的重要因素。同时，由于页岩脆性大，裂缝发育，表现出极强的应力敏感性[5-6]。张烨等[7]在2015年进行了页岩应力敏感实验研究，发现随着有效应力的增加，岩心渗透率呈递减趋势；雷浩等[8]在2019年基于毛细管模型，结合边界层和应力敏感理论，建立了页岩储层渗流新模型，证实了应力敏感效应是影响储层渗流特征的主控因素。所以，在进行页岩气藏产能评价时如若不完全考虑页岩吸附气与应力敏感的影响，这势必造成气藏产能评价不准，不利气藏合理开发。外国页岩气井主要采用放喷生产，几乎不对页岩气藏的产能进行评价[9]。而中国针对页岩气藏的产能二项式研究也较为稀少，肖缇[10]在2013年推导了页岩气藏水平井的二项产能公式，但在计算吸附气时存在缺陷并且尚未考虑页岩应力敏感的影响；张文龙等[11]在2016年引入儒柯夫斯基变换将水平井椭圆渗流场变换成圆形渗流场从而得到单组分气体的理想页岩气藏的水平井二项式产能公式，但未考虑吸附气和应力敏感的影响；刘华等[9]在2016年建立了多段压裂页岩气水平井拟稳态阶段产能方程，分析了裂缝参数和基质有效渗透率等参数对气井初始无阻流量的影响，但并未考虑页岩气吸附气和应力敏感的影响；李鹏[12]在2016年通过统计90口页岩气井的数据，发现其中72.2%的井无法运用传统二项式计算无阻流量，故基于传统二项式，利用线性回归方式建立了页岩气三项式产能方程，但并未对页岩气吸附气和应力敏感现象进行详细研究。

基于Forchheimer非达西渗流方程，考虑应力敏感和页岩吸附气的影响，建立了页岩气藏拟稳定渗流多级压裂水平井二项式产能方程并结合考虑压裂液影响的页岩气藏物质平衡进行方程求解参数，以某页岩气藏的一口典型多级压裂水平井实例论证本文二项式产能方程的可靠性。

1 考虑应力敏感和页岩吸附气的水平井二项式产能方程

根据宋传真等[13]回归出表征致密低渗气藏储集层应力敏感性的指数式关系式，页岩气藏考虑应力敏感的渗透率可以表征为

K=Kie-αk(pi-p)

(1)

式(1)中：K为考虑应力敏感的修正渗透率，D；Ki为气藏初始渗透率，D；pi为原始地层压力，MPa；p为气体压力，MPa；αk为页岩应力敏感指数，MPa-1。

中外研究学者通过大量吸附实验测量，普遍认同页岩气的解吸过程符合Langmuir等温吸附模型[14]，该模型中将吸附气量描述为在等温条件下与压力相关的函数，如式(2)所示。

(2)

式(2)中：V为单位体积岩石所吸附的标准状况下的气体体积，sm3/m3；p为气体压力，MPa；VL为Langmuir体积，表征页岩的最大吸附能力，sm3/m3；pL为Langmuir压力，代表气体吸附量达到极限吸附量的50%时所对应的压力，MPa。

肖缇[10]推导了页岩气藏水平井的二项产能公式，但尚存以下改进之处：①没有考虑页岩应力敏感特性；②计算吸附气含量时没有将孔隙体积与基质体积区分开来。现对页岩水平井体积压裂后(图1)的气藏进行简化并有如下假设：

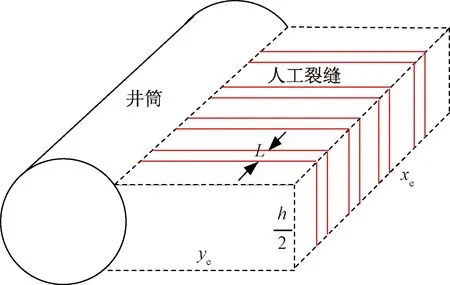
h为气层有效厚度，m；L为裂缝宽度，m；xe为射孔段长度,m;ye为压裂裂缝半长,m图1 页岩水平气井压裂简化图Fig.1 Shale horizontal gas well fracturing simplified diagram

①地层均质且各项同性且压裂裂缝完全延伸至气藏边界，水平井段位于气藏中心；②渗流过程为等温渗流；③气体在裂缝系统中流动遵循Darcy定律且忽略极小的启动压力梯度，裂缝与基质间不存在微观渗流，只存在吸附气解吸；④在生产过程中，产水较少或不产水时视为单相流动；⑤气体可压缩黏度恒定且忽略重力效应和毛管力影响。

根据Forchheimer方程[15]，考虑应力敏感的气体流动压力梯度可以表示为

(3)

式(3)中：ρ为气体密度，kg/ m3；v为气体速度，m/s；μ为天然气黏度，mPa·s；β为表征孔隙紊流影响的系数，m-1。

式(3)中βρv2非达西流动部分压降，代表在井轴周围流体的流动为非达西流。根据李士伦[16]在建立气井产能方程时，可忽略附加压降的影响，待建立方程后再将非达西流动能耗叠加到产能方程中。结合气体状态方程，qxsc可以表示为

(4)

式(4)中：qxsc为标准状况下流经x处的体积流量，sm3/d；N为裂缝条数；Z为气体偏差系数；T为气体绝对温度，K；Zsc为标准状况下气体偏差系数；psc为标准状况下气体压力，psc=0.1 MPa；Tsc为标准状况气体温度，Tsc=293 K。

当页岩气井处于拟稳定生产且地温恒定时，气井产气量等于吸附气解吸气量与游离气本身的弹性膨胀量之和。根据天然气等温压缩定义[16]，可以得到游离气的弹性膨胀量为

(5)

式(5)中：qe为游离气本身的弹性膨胀量，sm3/d；t为生产时间，d；Cg为标况下气体压缩系数，MPa-1；Vp为气藏孔隙体积，m3；φ为孔隙度。

结合前文介绍和式(2)，吸附气解吸气量可以表示为

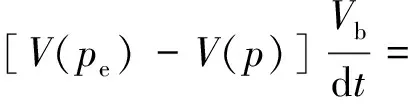
(6)

式(6)中：qd为吸附气解吸气量，sm3；Vb为页岩气藏基质体积，m3；V(pe)为未解吸时单位体积岩石所吸附的标准状况下的气体体积，sm3/m3；V(p)为压力p时单位体积岩石所吸附的标准状况下的气体体积，sm3/m3；Cg为标况下气体压缩系数，MPa-1。

因为气藏中任意一点处流过的流量qxsc与井筒到边界之间的气层流量qsc成正比，所以气藏中任意一点x处的流量为

qxsc=

(7)

拟稳态虽然是一种半稳定状态，但通常按稳定状态处理。因此，联立式(7)和式(4)，分离变量并积分后将表皮系数S和高速非达西项的紊流系数D引入，结合式(1)，引入拟压力整理化简得到考虑应力敏感的页岩气藏水平井产能方程为

(8)

2 考虑压裂液影响的地层压力表达式

页岩气藏在生产之初往往进行水平井多级压裂，大量压裂液被泵入地层，待到正式生产开始后随着天然气一起被采出地层，所以残存压裂液对地层压力的影响不容忽视。当气藏一直处于拟稳定生产状态，认为水在地层内不可压缩且忽略地层温度的变化。气藏生产一段时间后的累计产气量Gp与累计产气量Wp之和应等于相同生产时间内吸附气的累计解吸气量Gd、游离气自身的体积膨胀量Gf、页岩骨架变形量ΔVs、束缚水以及压裂液的膨胀量之和ΔVw，即

Gp+Wp=Gd+Gf+ΔVs+ΔVw=

Gd+Gf+VSRV(1-φ)cp(pi-p)+

(9)

(10)

式(10)中：m、a、n、b为岩石胶结指数、比例系数、饱和度指数和系数；Rw为地层水电阻率，Ω·m；Rt为地层电阻率，Ω·m。其中，付杰[17]在2016年对比分析了两种计算页岩气含气饱和度的方法，并确定了主要方法阿尔奇公式的相关系数：m=1.53、a=1.05、n=1.93、b=1.01、Rw=0.048 Ω·m。

结合式(2)得到累计解吸气量Gd的表达式为

(11)

基质和裂缝孔隙的中游离气因地层压力下降而发生膨胀，其的体积变化量表示为

(12)

式(12)中：Bgi为原始状态下天然气体积系数；Bg为气体压力p条件下所对应的天然气体积系数。

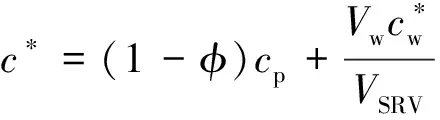
(13)

将式(13)中p近似替换为p/Z，pi近似替换为pi/Zi并移项变换得到p/Z与VSRV、Gp、Wp、φ等参数的关系为

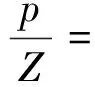
(14)

若已知地层参数、实际生产数据和VSRV等参数即可由求根公式求出p/Z，再根据p与Z关系式，基于二分法即可求出页岩气藏地层压力p。

3 实例计算

根据文献[18]，选取某页岩气藏1-3HF井生产截止至2014年12月31日，共计546 d连续生产的生产数据。该页岩气藏表现为异常高压，且边底水不活跃，试采过程不产地层水，部分地层参数见表1。

表1 气藏部分参数统计表Table 1 Partial parameter statistics table of gas reservoir

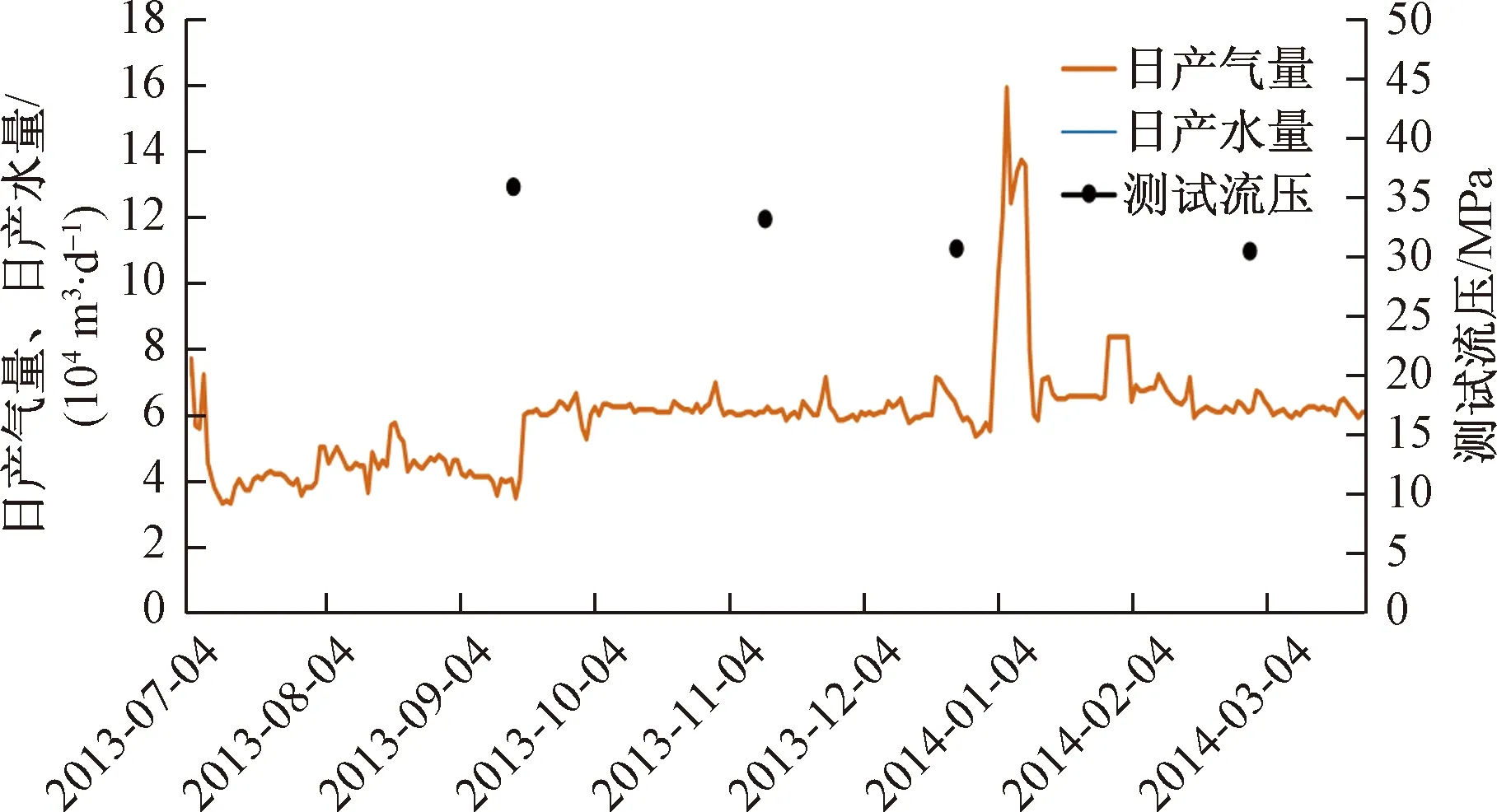
图2 生产曲线图Fig.2 Production curve diagram

选取总生产数据中前265 d生产数据(其生产曲线见图2)，采用罗钦平提出的改进遗传算法[19]进行计算机编程。改进遗传算法的实质是通过调整模型中的参数，对生产气井的实测井底流压进行拟合。具体模型计算步骤如下。

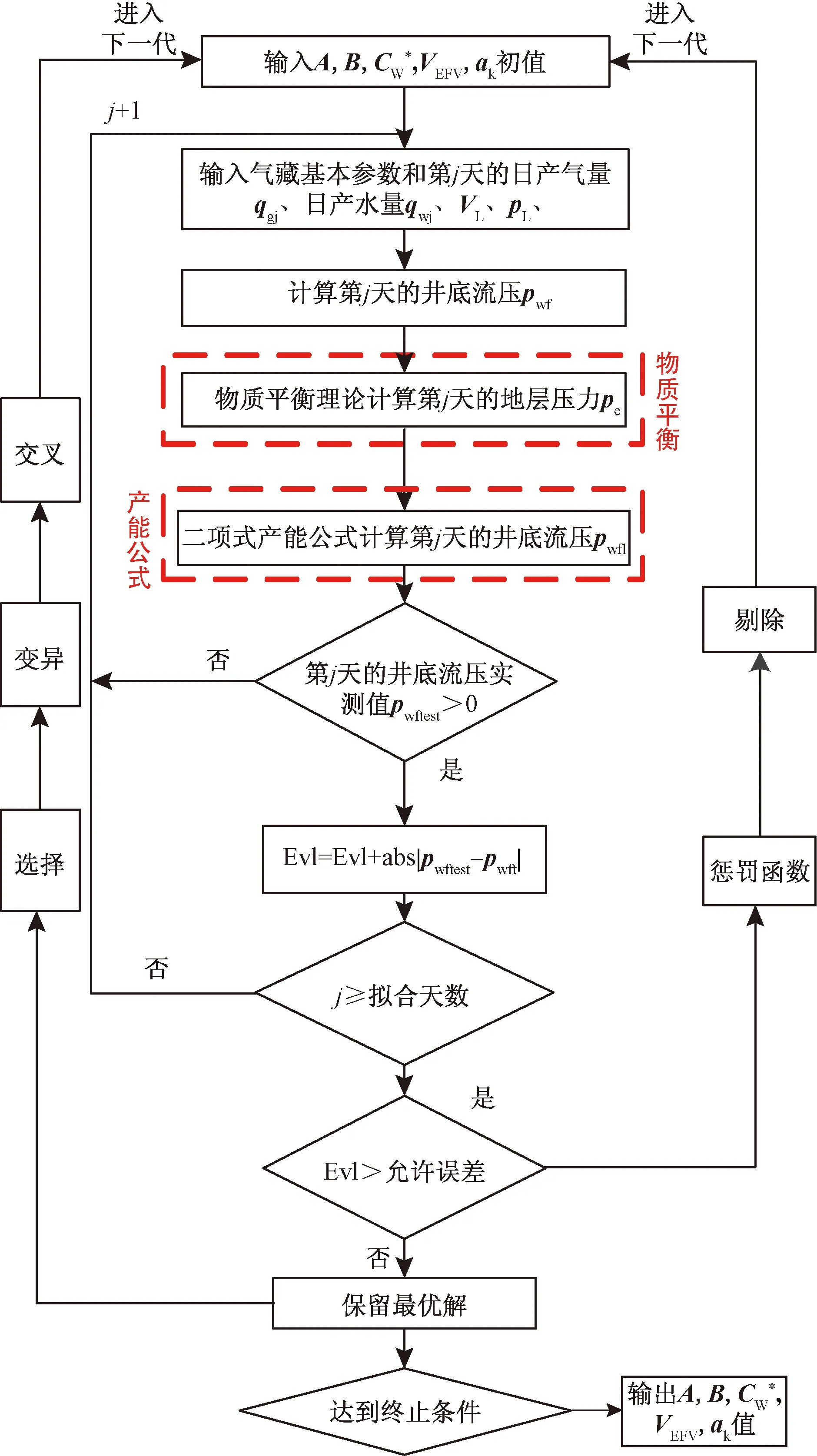
图3 计算流程图Fig.3 Calculation flow chart

步骤1在各个参数的物理范围内确定上、下界限的初始值，以所选气井生产时间段的前265 d为基础，将实测井底流压作为目标进行拟合计算，有关遗传算法的计算流程参看图3，本文中的遗传算法部分参数设置见表2。模型中，对于Δψ1和Δψ2分别采用数值积分的方法进行求解，气体的黏度与偏差系数分别根据积分微元段的平均压力进行计算。

表2 遗传算法部分参数统计表Table 2 Partial parameter statistics table of genetic algorithm

步骤2针对步骤1的拟合结果，若拟合效果较差时，调整已经逼近上、下限的参数，扩展参数取值范围重新计算直到获得良好的拟合效果。

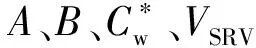
图4表明，遗传算法在本文模型的计算过程中种群进化正常，稳定性良好，拟合结果的可靠程度高。

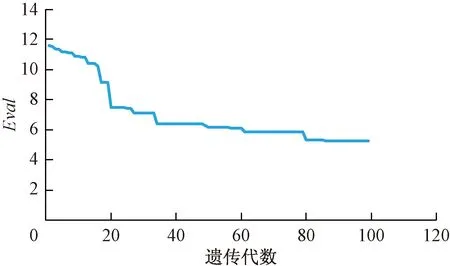
图4 Eval变化趋势图Fig.4 Eval change trend chart

通过以上计算流程，最终得到层流系数、紊流系数、压裂液和地层水的综合压缩系数、等效压裂体积和页岩应力敏感系数5个参数的数值如表3所示。根据拟合的参数结果，代入本文推导出的产能方程计算出该井的初始无阻流量为23.74×104m3/d。为了进一步研究气井可采储量的范围，根据拟合结果，采用新方法进行生产预测，该井先以日产气量6×104m3/d配产，期间稳产1 387 d；当井底流压下降至7 MPa开始定压生产，当日产气量下降至0.1×104m3/d关井，期间定压生产5 915 d，最终技术可采储量1.54×108m3。

表3 新方法计算结果Table 3 New method calculation result

表4和图5表明，基于前265 d生产数据，采用本文新方法拟合得到的井底流压与实测井底流压吻合程度相比另外两种方法精确很多，计算结果平均误差仅2.01%；图6中，由拟合参数结果进行后续281 d的井底流压和日产气量预测，因为实际生产中该井以定产生产，故日产气量预测值肯定会比较准确，但新方法的预测井底流压值与实测井底流压值平均误差仅2.02%。与此同时，基于该页岩气井的基础数据，分别采用肖缇[10]所提出的未考虑页岩应力敏感的计算方法与张文龙等[11]建立的未考虑吸附气和应力敏感的页岩气藏水平井产能计算对1-3HF的产能进行计算和预测。结果表明，当未考虑吸附气和页岩应力敏感时，两种方法的预测值均有所偏差。因此，下面针对本文建立的模型特点进行详细分析。

表4 计算结果误差对比表Table 4 Calculation result error comparison table

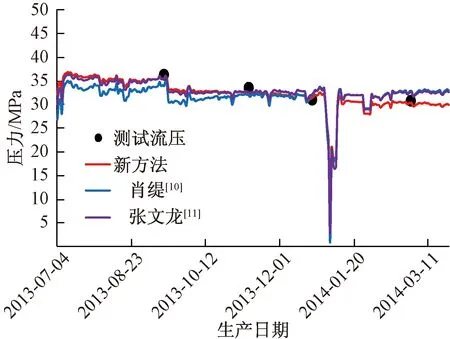
图5 三种方法井底流压拟合结果对比图Fig.5 Comparison diagram of three methods of bottomhole flow pressure fitting results

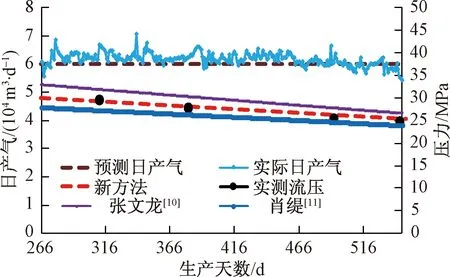
图6 三种方法井底流压预测结果对比图Fig.6 Comparison diagram of three methods of bottomhole flow pressure prediction results

(1)考虑应力敏感和页岩吸附气的影响，建立了页岩气藏拟稳定渗流多级压裂水平井二项式产能方程并结合考虑压裂液影响的页岩气藏物质平衡方程进行求解，建立了新型的页岩气藏产能预测方法。

(2)模型中考虑了页岩气藏地层压力随开发的进行会发生变化，这对流体渗流的影响是不容忽视的，而常规的产能方法之中并未考虑这一因素。

(3)基于气井的历史生产数据，采用本模型能够对页岩气藏的地层压力进行定量的预测计算，大大减少了实际开发中对页岩气藏地层压力的估算误差以及测量成本。

(4)依据本文模型对气井历史拟合的参数结果，进一步对气井的技术可采储量进行预算，从而得到气井的技术可采储量，为气井开发提供有力的指导。

综上所述，基于考虑压裂液影响物质平衡求解的新型页岩气二项式产能方程可靠性较高。

4 结论

(1)从气藏渗流理论出发，结合多级压裂水平井特征和页岩吸附气特性，将应力敏感系数引入Forchheimer渗流方程，推导了考虑吸附气和应力敏感的页岩气藏多级压裂水平井二项式产能方程。

(2)考虑压裂液含量，基于页岩气物质平衡建立了页岩气藏地层压力与累产气量、累产水量、等效压裂体积等参数的关系表达式。

(3)以某页岩气藏典型水平井生产数据为基础，结合改进的遗传算法和地层压力表达式进行计算机编程，利用前265 d生产数据对实测井底流压进行拟合(误差仅2.01%)，求取层流系数、紊流系数、压裂液和地层水的综合压缩系数、等效压裂体积和页岩应力敏感系数5个参数，得到考虑吸附气和应力敏感的页岩气藏多级压裂水平井二项式产能方程。

(4)由拟合得到的新二项式方程对后续281 d的日产气量和井底流压进行预测，预测值与实测值吻合良好(误差仅2.02%)，相比已有方法精度更加准确，计算出该井初始无阻流量为23.74×104m3/d；同时进行生产预测，后续稳产1 387 d，定压生产5 915 d，最终技术可采储量1.54×108m3。计算结果表明，考虑应力敏感和页岩吸附气的影响的页岩气藏拟稳定渗流多级压裂水平井二项式产能方程可靠性较高，采用此二项式产能方程用于进行页岩气动态产能评价更为合理，更能反映气藏的真实情况。