郭氏弹性地基梁法与有限单元法在泵房基础应力分析中的应用
2020-04-22陈新佳
陈新佳
(辽宁省水利水电勘测设计研究院有限责任公司,辽宁 沈阳 110006)
随着国内城镇规模的不断扩大,引调水工程项目发展非常迅速。泵站作为此类工程中的重要组成部分,在保证水资源的合理调度和管理方面起着不可替代的作用。本工程位于凌源市应急供水工程四级泵站中的头部位置,头部泵站进水前池的上游为青龙河,河流多年水位变化不大,流量较稳定,泵房基础下部地质主要分两层:上层为砂砾石,下层的全风化岩较深,地基承载力验算后满足设计要求。泵站基础设计为筏型基础结构,选择该类型的主要优点有:结构整体性好,适用于各种地基条件,自身重量大,抗浮和抗滑稳定性较好[1]。
1 荷载组合及模型建立
1.1 郭氏法计算模型及荷载组合
头部泵房基础尺寸为48.89m×12.94m,厚度为1.5m,长度方向设有沉降缝。模型按照平面变形问题考虑,即地基是半无限空间体,基础结构在短跨方向各截面形状和尺寸相同,同时荷载也是均匀分布的。据此假定建立地基梁模型,主要荷载考虑地上、地下部结构在基础边缘产生的轴向力、弯矩,考虑单台设备均布荷载,考虑侧向土压力在基础边缘产生的弯矩。根据设计报告中地震基本烈度为Ⅵ度,未考虑地震荷载;根据地质报告中地下水埋深较深情况,未考虑泵房下部结构受到地下水带来的浮力及扬压力,工况及荷载组合见表1。
对表1中各工况下的荷载组合进行比较后,确定最高水位运行期工况(前池水位最低)为最不利工况,即设计计算的控制工况。
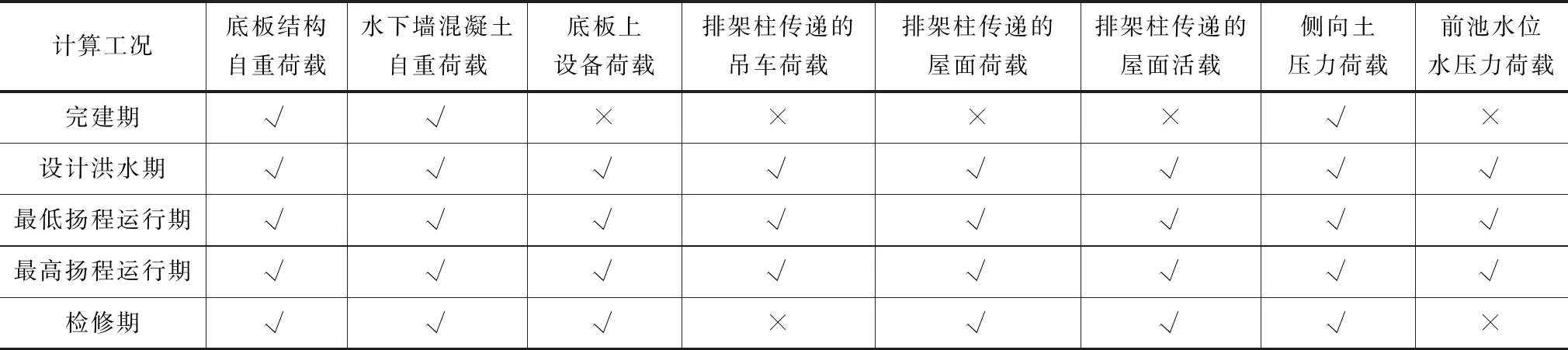
表1 青龙河头部泵站各工况荷载组合表
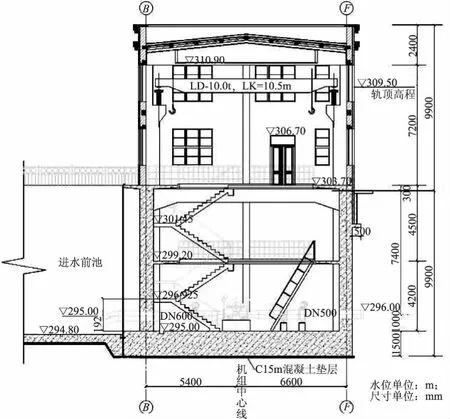
图1 头部泵房剖面图
1.2 有限元法计算模型及荷载组合
头部泵房的有限元模型取跨度为两轴线间距12m宽作为计算对象,宽度内取整个泵房上、下部结构作为计算对象,地基范围取为2倍泵房模型高度,平面方向延伸2倍泵房模型跨度[2];考虑基础、结构和地基的相互作用,上部房顶结构作为荷载传递至立柱上。主泵房共两层,分为地上及地下部分。其中上部结构(包括屋面、吊车梁及排架)总高9.6m,排架柱中间为填充砖墙;下部结构总高10.2m,为钢筋混凝土结构,排架柱及下部结构侧墙与基础底板整体浇筑,剖面如图1所示。
2 郭氏弹性地基梁法的泵房基础内力
2.1 郭氏法地基反力求解方法
应用郭氏法求解地基对基础的反力时,一般先根据实际情况假定地基反力分布规律表达式,基于半无限体模型的郭氏法将梁下任意一点的地基反力p(x)近似地表示为有限项幂级数,即
p(x)=a0+a1x+a2x2+…+anxn
(1)
式中,ai(i=0,1,2,…,n)—待定的常系数。
再利用以下两个方程建立包含ai常数的线性方程最终求得。
(1)基础梁在荷载和反力共同作用下,挠度微分方程为
(2)
式中,E,I—基础梁的弹性模量、截面惯性矩;q(x)—梁上荷载。
平面问题中,半无限大弹性体由弹性理论导出的计算公式为
隰县作为一个国家扶贫开发工作重点县,脱贫攻坚进入冲刺阶段,农村安全饮水工程也不断加码。饮水安全工程不仅为老百姓送来了健康,也让不少农民借“水”生财。
(3)
式中,P—在半无限大弹性体边界上的集中力;s—任意点至P的距离;r—要求其沉降的点至P的距离;E0,u0—地基的压缩模量及泊松比。
根据基础梁与地基之间不会出现拉力,在荷载作用下,梁与地基紧密接触,即变形连续假定,得到变形连续方程y(x)=W(x),求得各个常数,再代入式(1)求得地基反力p(x),最终利用截面法求得梁的内力。当郭氏法中p(x)所取级数项数越多,结果的准确性越高[3]。
2.2 郭氏法查表计算结果
查表前,需对地基梁按照柔性指数t对梁进行分类,计算公式如下:
(4)
式中,l—梁的一半长,h—梁的厚度。
根据柔性指数取值范围可以将基础梁分为3类:刚性梁(t<1)、有限长梁(集中荷载1≤t≤10,均布荷载1≤t≤50)、无限长梁(集中荷载t﹥10,均布荷载t>50)。其中前两类按照短梁查表计算,第三类按照长梁查表计算。地基压实模量E为4.47MPa;梁弹性模量为2.8×106t/m。
本文根据公式计算后得到底板地基梁柔性指数t为0.12<1,应按照短梁查表。采用1.1节中最不利荷载组合计算得到的结果如下:
屋面及吊车荷载:弯矩(M)为±107.5kN·m,向下轴力(↓)为50kN;
上部砖墙结构荷载:向下轴力(↓)为78kN;
下部混凝土结构荷载:向下轴力(↓)为175kN;
单台设备荷载:向下轴力(↓)为58kN;
下部混凝土承受侧向土压力荷载:弯矩(→)为570kN·m;
下部混凝土承受前池最低水位水压力荷载:弯矩(←)87kN·m。
通过查表得到地基梁分段弯矩控制值(→)为751kN·m,剪力值(↓)为263kN;再由材料力学应力求解公式得到地基梁分段最大应力σmax为1.422MPa,在地基梁端部与前池连接位置。
3 基于有限单元法的泵房整体三维模拟
3.1 有限单元法求解过程分析
采用SolidWorks进行三维实体建模,并通过与有限元分析软件提供的通用格式对泵房进行受力模拟,其中混凝土采用SOLID 65单元模拟,软件模拟的8节点3D实体单元能实现开裂、压碎及温度升降应力、应力释放等特性。混凝土本构关系模型采用软件默认的理想弹塑性本构模型,同时采用非线性拉应力准则及混凝土多参数破坏准则[4]。
主泵房采用上、下部结构与泵房底板整体建模方式,软件计算分析时选取其中一跨12m进行模拟(同郭氏法),整个有限元模型8节点六面体等参单元共有27256个,节点36439个。三维有限元模型网格如图2所示。

图2 三维有限元模型网格划分图
泵房荷载包括传至牛腿柱的屋面荷载、吊车荷载采用集中力的加载方式;底板上设备荷载采用面荷载的加载方式;两侧混凝土墙体上的土压力及前池侧向水压力采用应力梯度以面荷载的方式施加(工况及主要荷载组合同表1)。由于底板的刚度较大,故可以看作埋置于土中的刚性基础,将地基底部所有节点进行Y方向的自由度约束,而纵向墙体边界上的节点进行X和Y两个方向的自由度约束[5],依据此约束计算得到的泵房进水侧在控制工况下(最高扬程)的最大应力。
3.2 泵房整体稳定有限元计算结果
根据有限元原理中协调关系与本构关系原理及平衡方程,应用软件对模型进行分析,计算参数、工况及荷载组合在1.2节中已经介绍,求解采用最不利工况下节点的位移、应变和应力,以便同郭氏弹性地基梁法进行对比。在此基础上,应用有限元法三维整体建模,不仅可以得到基础内力分布图,亦可得到泵房上、下部结构的整体内分布图,软件计算得到的模型整体结构应力云图如图3—5所示,X、Y方向应力云图如图4—5所示。
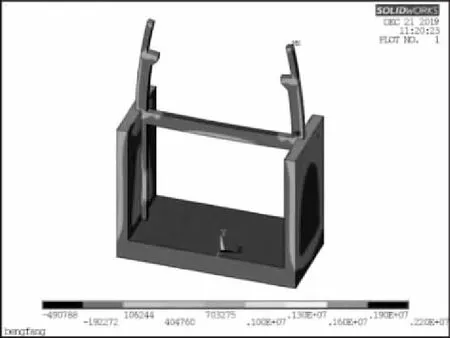
图3 第一主应力云图
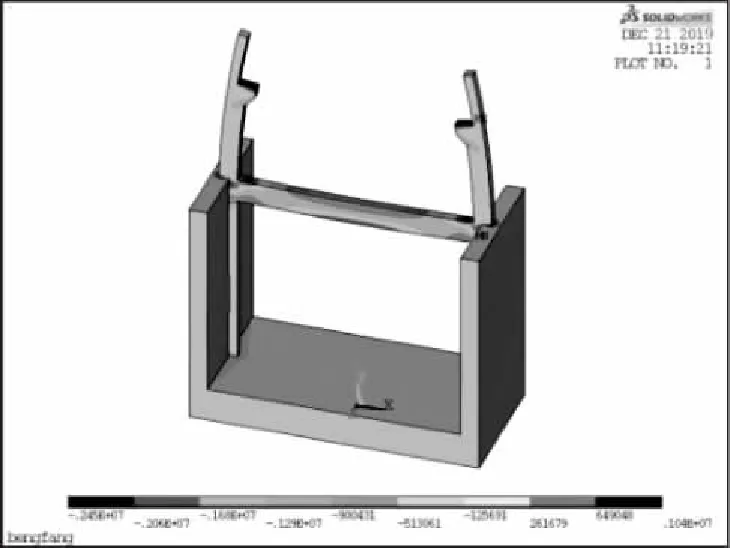
图4 X方向应力云图
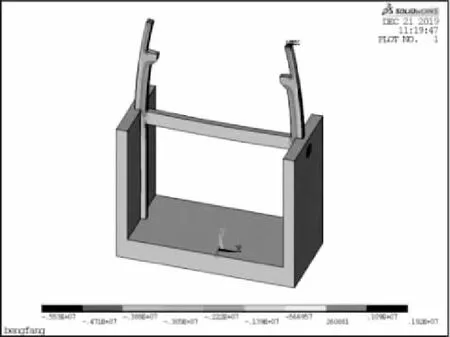
图5 Y方向应力云图
由软件分析结果可以看出,泵房底板混凝土最大拉应力位于底板边缘下侧与前池连接位置,拉应力值为1.398MPa,此值与郭氏弹性地基梁法计算结果较接近,说明模型假定的边界条件符合实际情况。
此外,图4—5中泵房底板上部电机和水泵压应力值为0.567MPa,分析时还需考虑事故工况水锤压力,故推测在设备底部中心底板所受应力较大(具体值在打压试验后通过相关数据进行模拟),应加强配筋;分析结果中排架中部分牛腿以下最大拉应力为1.1~1.5MPa,位置在柱与梁、墙相交处,此处也需加强配筋。而混凝土墙体内的下柱段应力较小,配筋时可与泵房水下墙一并考虑,亦符合以往的工程设计经验。
4 结论
(1)郭氏法在计算假定半无限弹性地基模型时,反映了地基的连续整体性,计算模型相对简单,可通过编程提高方程幂级数,从而提高计算精度,对于厚土层或整体岩石基础的求解较适用[6]。但模型无法反映地基土非弹性性质和分层复杂性,因此在应用时需注意所选场地的地质复杂程度。
(2)本文应用郭氏法对比有限元软件进行模拟分析,得到结果基本相同,复核了有限元法在建模及参数、边界条件设置时的正确性。分析有限元计算最大应力值略小于郭氏法的最大应力值,这是建模时将泵房底板与排架柱、水下墙整体考虑的结果。
本文将两种方法应用于具体案例,计算弯矩、剪力值符合工程实际,在泵房、水闸等筏型基础的结构设计[7- 10]、配筋计算中具有一定参考价值。
