某链式自动炮分度机构刚柔耦合动力学特性研究

王 凯，李 勇，田 楠，申亚琳

(西北机电工程研究所，陕西 咸阳 712099)

链式自动炮是一种通过链条周向转动驱动炮闩往复运动来完成解锁、开闩、抽筒、供弹、输弹、关闩、闭锁、击发等动作的外能源自动炮[1]。分度机构作为链式自动炮的关键分度机构，负责协调链式自动炮进弹轮与各传动系统间的运动关系，对链式自动炮运动的准确性和协调性起着重要作用[2]。

目前，分度机构的相关研究主要集中在两个方面：一方面，通过对分度机构的分度轮轮廓曲线、中心距、分度滚子数等进行参数化理论设计，得到较优的传动效果[3-4]。另一方面，考虑机构变形对分度机构的动力学特性影响，通过建立与实际工况环境相符的刚柔耦合动力学模型和动力学虚拟样机，模拟不同因素对其动态性能的影响。分度机构参数化理论设计已趋于成熟，鲜有创新改进。分度机构的现有刚柔耦合动力学研究，大多以ANAYS、Pro/E、ADAMS三种平台，基于模态缩减法建立分度机构的刚柔耦合动力学模型，进行不同因素对其扭转振动和最大加速度影响[5-6]。基于模态缩减法建立的刚柔耦合动力学模型，存在无法直接建立模态柔性体与其他构件的接触、模型修改困难繁杂、只能描述小变形的线性变形等缺点。有限元柔性体技术则可有效地避免上述问题[7]。另外，链式自动炮分度机构传动具有高速、瞬时强冲击等特点，其传动过程中的碰撞力极大影响整体系统的可靠性、构件疲劳寿命等。显然，上述分度机构的刚柔耦合动力学研究未对传动过程中的冲击碰撞特性进行相关研究。

因此，本研究以分度机构中的输出轴作为柔性体，其余构件作为刚性体，采用有限元柔性体建模原理，基于UG三维软件和Recurdyn多体动力学分析软件建立分度机构的刚柔耦合动力学模型，研究不同因素(粘性阻尼系数、分度轮输入转速、啮合间隙)对传动过程中的碰撞力影响，为分度机构的设计与优化提供依据。

1 链式自动炮分度机构

链式自动炮示意图如图1，其工作原理如下：电机动力经过一对换向齿轮传动分为两路，第一路通过链条往复运动驱动闩体完成进弹、闭锁、击发、抽壳等动作；第二路经分度机构驱动进弹轮转动，完成拨弹动作。两路运动通过分度机构协调各传动系统间的运动关系，实现供弹与输弹动作的交接过程。

分度机构是一种将输入轴的连续转动转化为输出轴间歇转动的传动机构。在链式自动炮中，其间歇运动频率与链式自动炮的射速匹配一致，属于高速高精度运动，具有瞬时强冲击碰撞特点。高速运动加剧传动过程中的冲击碰撞，影响系统整体传动的稳定性。同时，强冲击碰撞使得分度机构的啮合情况恶化，加速磨损运动构件，产生啮合间隙，进一步恶化传动工况环境情况。

图1 链式自动炮示意图

2 分度机构刚柔耦合多体动力学建模

2.1 有限元柔性体理论

有限元柔性体MFBD(Multi-Flexible-Body Dynamics)首次实现了有限元技术与多体动力学的有机结合，克服了模态柔性体的缺点，采用节点之间的相对位移和旋转作为节点坐标来描述结构的变形，具有较高的计算精度[8-9].理论数学建模原理如下：

在空间梁单元结构中，取任意两单元i-1和i，如图2所示。坐标系X-Y-Z为总体惯性坐标系；xk-yk-zk为节点k的节点坐标参考系；rk表示节点k在总体惯性坐标系的位置矢量；x(i-1)i-y(i-1)i-z(i-1)i为固结在节点i上，关于节点i-1的随体坐标系。

图2 梁单元变形示意图

节点i在惯性坐标系X-Y-Z中的位置矢量分别用节点i-1的位置矢量，以及与节点i-1相对变形表示为

(1)

相对角速度wi与wi-1的关系可表示为：

(2)

通过对式(1)、式(2)利用虚位移原理进行变化并联立，可得相邻节点虚位移关系。反复递推就可以得到整个系统节点之间的相对虚位移关系

δZ=Bδq

(3)

同理，对式(1)、式(2)求导，联立得到系统在惯性坐标系下的节点速度与相对速度的关系；节点的加速度可通过上述速度关系求导获得。

系统运动在惯性坐标系下的Euler-Lagrange基本方程，如下：

(4)

式中，Φ为约束矩阵；λ为拉格朗日乘子。

将式(3)代入到式(4)中，得到

(5)

由于δq是任意的，从而得到系统的动力学方程为：

(6)

2.2 建立几何模型

分度机构采用双层共轭滚柱凸轮驱动，用于两轴间的传动，主要由分度轮、输出轴、滚子、滚子帽组成，如图3所示。分度轮由前片凸轮和后片凸轮组成，前、后片凸轮的轮廓曲线一致，呈一定角度错开。滚子呈两层均匀安装在输出轴上，与前、后片凸轮啮合。

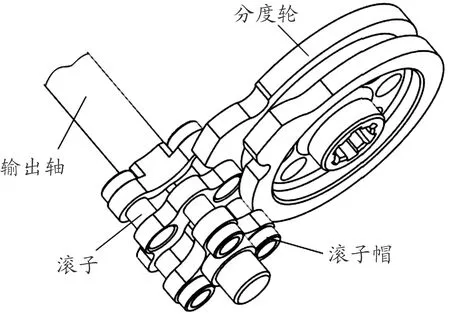
图3 分度机构组成示意图

几何模型建立过程如下：基于分度轮外轮廓曲线、压力角、中心距等，利用Matlab软件编程得到分度轮外轮廓数据；基于分度轮轮廓数据云，利用三维建模软件UG绘制某链式自动炮分度轮并与其他构件装配；将UG装配模型导入到多体动力学仿真软件Recurdyn中，设置材料属性:弹性模量2.06×1011Pa、剪切模量7.782×1010Pa、密度7.85×103kg/m3。本研究采用的分度轮外轮廓曲线如式(7)所示，式中，θ分度轮角位移；φ为输出角位移；θf=52°；h=2.6；θ1=5.846 2°；θ2=46.153 8°。

(7)

2.3 施加约束和接触

根据分度机构构件的连接和运动关系，在Recurdyn软件中建立约束和接触如表1所示。其中，分度轮与滚柱之间的Extend Surface to Surface Contact面接触计算是一个不断检测的过程，根据穿透深度及变化来计算接触力。当计算过程中分度轮与滚子的实际穿透深度小于最大穿透深度时，计算接触力；一旦检测到实际穿透深度大于最大穿透深度，则接触失效，不再计算接触力[7-8]。本文根据工程经验设置最大穿透深度0.1 mm。接触理论采用非线性弹簧阻尼模型，其法向接触力计算公式：

(8)

(9)

(10)

式中：k为接触刚度系数；c为粘性阻尼系数；δ为接触穿透深度；m1为刚度指数；m2为阻尼指数；m3为凹痕指数；μ1、μ2为接触物体材料的泊松比；E1、E2为接触物体材料的弹性模量。

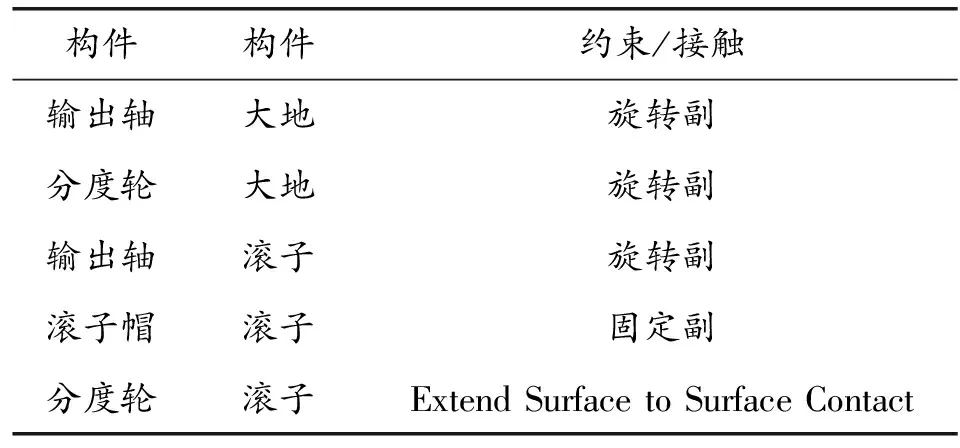
表1 分度机构约束和接触

2.4 刚柔耦合多体动力学模型

链式自动炮分度机构输出轴的动力学特性体现分度运动的准确性。综合考虑仿真精度、计算速度等因素，本文对分度机构中的输出轴利用Recurdyn软件中的mesh工具进行了有限元柔性化处理，其余构件依旧作为刚性体。输出轴经过有限元处理后，在滚子绕输出轴旋转运动副以及输出轴旋转运动副处自动生成了刚性单元(FDR单元)，方便运动和接触关系的建立。分度机构的刚柔耦合多体动力学模型如图4所示。

3 不同因素刚柔耦合动力学响应分析

经过多次工程实践经验发现，分度轮输入转速、啮合间隙、粘性阻尼系数对链式自动炮分度机构运动特性起主要影响作用。因此，本文以此三因素为变量，研究传动过程中的碰撞力变化规律，为分度机构的设计与优化提供依据。

1)粘性阻尼系数

分度轮与滚子接触模型利用非线性阻尼模型来计算粘性阻尼系数，该模型认为物体表面接触-碰撞过程中的能量是由粘性阻尼引起的。该阻尼与刚度系数、接触穿透深度、碰撞速度、弹性恢复系数有关，上述参数又与接触物体的材料、碰撞表面曲率、润滑脂的粘度等有关，很难进行精确计算。根据工程经验，粘性阻尼系数一般取刚度系数的0.1%～1%[10]。刚度系数利用式(9)、式(10)代入分度轮和滚子的相应的材料参数为5.81×105N/mm。因此，本文结合仿真情况取0～800 N·S/mm作为粘性阻尼系数的参数范围。

2)分度轮输入转速

分度机构中分度轮输入转速与链式自动炮射频相匹配，高射频加剧了分度过程中冲击碰撞情况，影响供输弹系统运动的准确性和可靠性。因此，本文结合链式炮实际射频情况取200～600发/min作为分度轮输入转速的参数范围。

3)啮合间隙

安装误差和加工误差产生的间隙直接影响分度盘与滚子的啮合情况，从而影响传动的平稳性和准确性。另外，随着啮合磨损的累积，滚子和分度轮之间的啮合间隙会变得越来越大，且无法避免。因此，本文结合实际工程情况取0.1～1 mm作为啮合间隙的参数范围。

3.1 粘性阻尼系数影响

为研究接触阻尼系数对于分度机构动力学特性的影响，在分度轮输入转速300 r/min、啮合间隙0.1 mm时，粘性阻尼系数分别取0、100、…、700、800 N·S/mm。从图5得出，随着粘性阻尼系数的增大，碰撞力曲线规律不再平稳，尖点毛刺增多。提取出不同粘性阻尼系数的最大碰撞力特征值如表2所示，并绘制出图6所示的曲线，可知：碰撞力最大值随粘性阻尼系数增大整体呈先缓慢、后急剧递增趋势。在0～200 N·S/mm区间增大时，碰撞力最大值呈现近似线性缓慢递增趋势，递增率2 475 N/100(N·S/mm)；在200～800 N·S/mm区间增大时，碰撞力最大值整体呈现急剧递增趋势，最大递增量30 706 N/100(N·S/mm)。

图5 粘性阻尼系数与碰撞力关系曲线

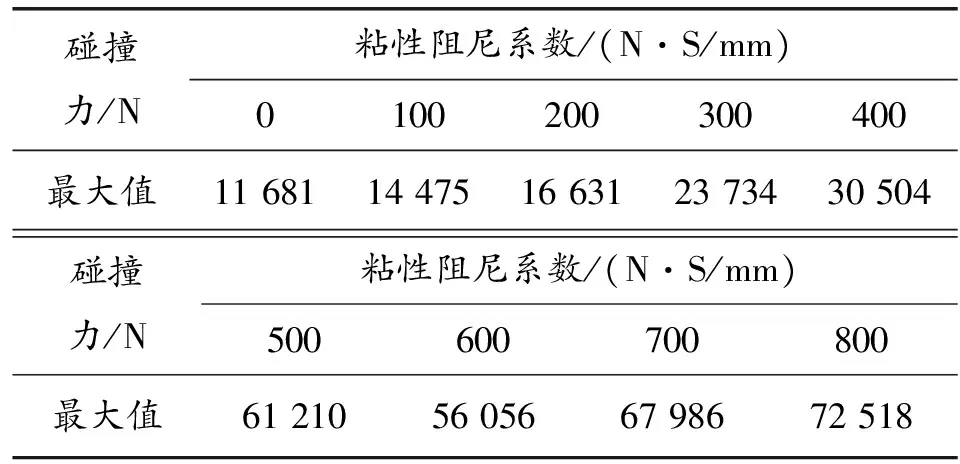
表2 不同粘性阻尼系数下的碰撞力特征值

图6 粘性阻尼系数与碰撞力特征值关系曲线

3.2 分度轮输入转速影响

为研究分度轮输入转速对于分度机构动力学特性的影响，在接触阻尼系数100 N·S/mm、啮合间隙0.1 mm时，分度轮转速分别取200、250、…、550、600 r/min。从图7得出，随着分度轮转速的增大，碰撞力曲线规律变化不明显，尖点毛刺幅值增大。提取出不同分度轮转速的最大碰撞力特征值如表3所示，并绘制出图8所示的曲线，可知：随着分度轮转速的增大，碰撞力最大值呈现近似线性递增趋势，递增率2 475 N/50(r/min)。

图7 分度轮输入转速与碰撞力关系曲线

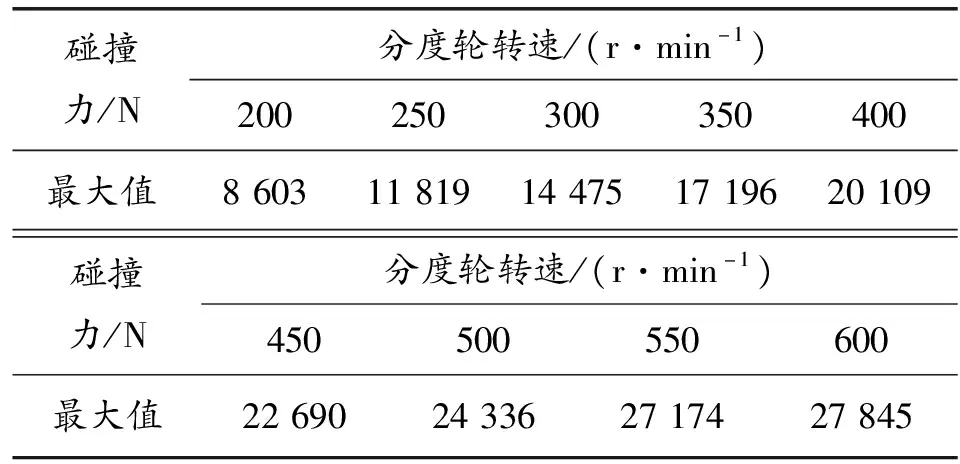
表3 不同分度轮输入转速下的碰撞力特征值

图8 分度轮输入转速与碰撞力特征值关系曲线

3.3 啮合间隙影响

为研究啮合间隙速对于分度机构动力学特性的影响，在粘性阻尼系数100 N·S/mm、分度轮转速300 r/min时，啮合间隙分别取0.1、0.2、…、0.9、1 mm。从图9得出，随着啮合间隙的增加，碰撞力初始位置变化复杂，碰撞力曲线在0.5 mm间隙处出现急剧增大趋势。提取出不同啮合间隙的最大碰撞力特征值如表4所示，并绘制出图10所示的曲线，可知：碰撞力最大值随啮合间隙增大整体呈先较低值稳定、后急剧增加减小、再较高值稳定的趋势。啮合间隙在0～0.4 mm区间增大时，碰撞力最大值稳定在12 860～14 475 N区间；啮合间隙在0.4～0.7 mm区间增大时，碰撞力最大值呈现先急剧增大后急剧减小趋势，碰撞力最大值71 481 N；啮合间隙在0.7～1 mm区间增大时，碰撞力最大值稳定在20 127～24 434 N区间。

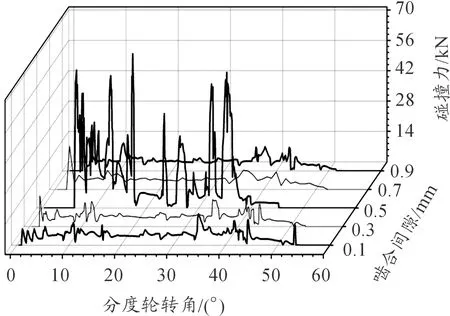
图9 啮合间隙与碰撞力关系曲线

表4 不同啮合间隙下的碰撞力特征值

图10 啮合间隙与碰撞力特征值关系曲线

4 结论

1)在其他参数固定的情况下，链式自动炮分度机构碰撞力最大值随粘性阻尼系数增大整体呈先缓慢、后急剧递增趋势；随着分度轮转速的增大，碰撞力最大值呈现近似线性递增趋势；随啮合间隙增大整体呈先较低值稳定、后急剧增加减小、再较高值稳定的趋势。

2)链式自动炮分度机构参数范围选取粘性阻尼系数0～200 N·S/mm、啮合间隙0～0.4 mm、分度轮输入转速200 r/min时，碰撞力最大值相对较小，即对其供/输弹运动的准确性和可靠性的影响较小。