任意地基系数下闭合框架结构变形计算探讨
2020-04-20梅新


摘 要 结构设计中常采用荷載结构法和地层结构法,本文主要采用后者,选取多种不同的地基系数,进而探讨任意地基系数结构的内力以及变形特点,从而优化结构设计。
关键词 结构荷载法;任意地基系数;变形计算
引言
城市地下空间的开发和利用是造福后代的新型资源储备和手段。地下空间的使用在某些方面上缓解了城市土地资源压力,在一定程度上解决了资源纷争,是城市未来重要发展方向之一。
目前地下结构设计中,常采用荷载结构法和地层结构法[1-2],前者的基本理论体系为结构力学原理,计算快捷,应用广泛;后者依托于计算机的各种有限元软件进行数值模拟计算,可以模拟地下结构的开挖过程,但对于参数的要求严格且计算复杂。本文主要兼顾以上两种设计方法,采用控制变量法,简要分析任意地基系数结构的内力以及变形特点。
1工程实例
本文以某一地下结构工程为例,依据其工程概况和地质条件获取计算条件如下:该结构净宽 12m,净高9m,底板厚度500mm,侧板厚度500mm,结构顶板厚度500mm,埋深为5m。采用钢筋混凝土结构,其平面形状为矩形,淤泥质黏土为主,混凝土弹性模量E=2.95Gpa,开挖面以上无活荷载。荷载主要考虑结构自重及围岩压力。
2参数选取
2.1 物理力学参数
其材料物理、力学指标如下:钢筋混凝土容重25KN/m3弹模29.5Gpa,泊松比0.2。土体重度17.3KN/m3,黏聚力9.6Gpa,内摩擦角9.1°,荷载考虑结构自重及围岩压力。
2.2 荷载计算
(1)作用在结构上的荷载
①顶板永久荷载:
考虑结构自重
②地层竖向土压力:
由于埋深15m
(2)底板上永久荷载
①底板自重:
(3)结构刚度:
(4)结构截面弯矩:
(5)弹性模量:
3计算分析
3.1 模型建立
运用Feon有限元法去求解,在程序起始条件中输入混凝土弹性模量E1=2.95GPa、宽度为单元1的情况下截面面积A=0.5m2、截面设计厚度为500mm,则计算出支撑惯性矩为I=0.0104m4、结构刚度EI=3.068×106N/mm。参数输入完毕后,将建立的模型输入其中,假设结构侧面区域为弹性抗力每隔0.5m设置弹簧则包括坐标点(0,-i*0.5),i∈[0,18]。结构底部考虑弹性抗力为常数每隔一米设置一个弹簧包括坐标点(0,-9.5)至(12,-9.5)共12点,考虑弹簧长度为0.5m,故考虑以上坐标点及参数并进行模板化可以得到如下图3.1的结构计算模型。
在计算常数模型变形及内力的时候,假设地下结构的底部弹性抗力为固定值15000KN/m2,且依次考虑结构侧面的弹性抗力为(a)沿深度呈常数分布、(b)沿深度呈梯形分布、(c)沿深度呈抛物线(上小下大)分布三种形式,分别进行计算。
3.2 相关计算分析
(a)情形:假设地基系数为常数,K1=15000KN/m,K2=10000KN/m,其内力和变形计算结果如下图3.2所示。(Mz为弯矩、Ty为轴力、N为剪力下同)。
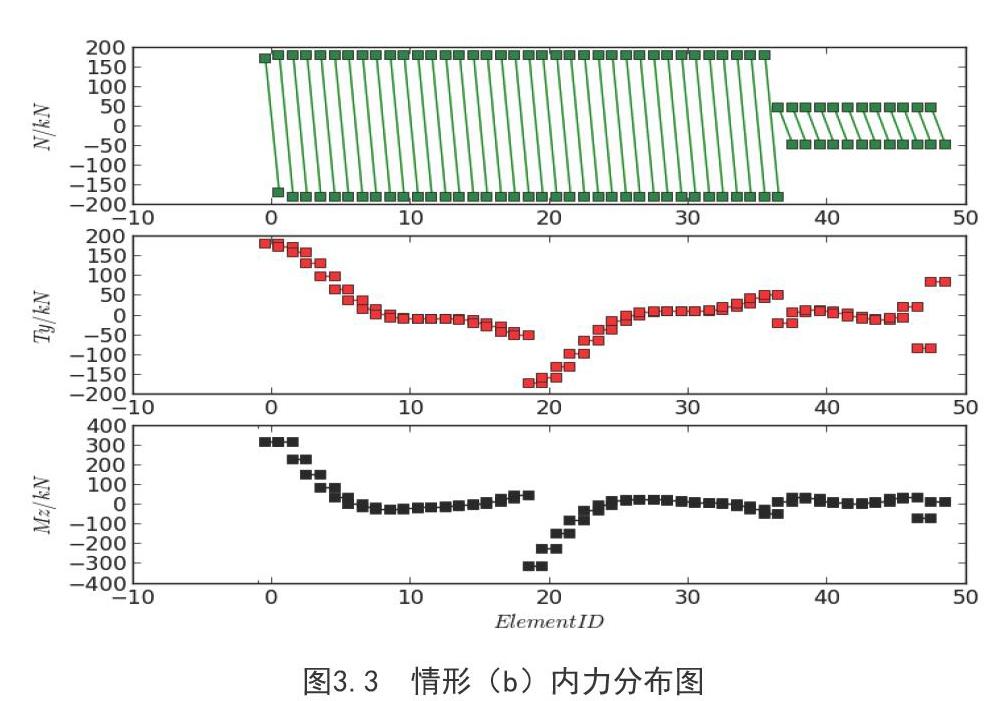
(b)情形:假设地基系数为线行分布在结构区域内最小值Kmin=5000KN/m,最大值Kmax=15000KN/m,地基系数函数表达式为Y=10000/9*X+5000,其内力和变形计算结果如下图3.3所示。
(c)情形:假设地基系数为二次分布在结构区域内存在最大值Kmax=15000KN/m,抛物线方程为Y=43.2x2+500x+7000,其内力和变形计算结果如下图3.4所示。
若采用将三个变形分布图置于一个程序中,即可获取不同情形下的变形对比分析图,如图3.5所示。
3.3 结果与分析
由以上计算结果分析可知:
(1)地基系数常数型分部下结构的变形
在常数型地基系数下,墙体变形情况在顶部是变形最小的,仅在4.0mm-4.5mm之间。结合图3.2.7得知:在地基系数为常数的情况下,其弯矩是三者之间最大的。由于结构顶端的约束,导致了位移在三者之间最小。在区域y∈[0,-2]之间达到最大变形,即使在结构的约束下,但是变形仍在增大。在y∈[-2,-5]时发生变化,变形逐渐收缩;在基坑底部y=-5之后,变形又开始变化且在y=-8时达到最值,并随后发生收缩。因此在设计该结构的时候,应该考虑到此问题,对变形较大位置重点支护,保证基坑开挖的过程中,能尽量控制好结构的变形且不影响施工的进程以及周边环境。
(2)地基系数线性分部下结构的变形
在线性地基系数,墙体变形在y=-1.5时达到最值,约5mm;结构整体变形在y<-1.5时呈为递减趋势。表明在该地基系数的情况下,变形会随着土层的加深而变小,且在此之后的变形接近于常数分布,但总体上要小于常数分布变形。
(3)地基系数二次函数分布下结构的变形
抛物线型地基系数的变形情况介于(a)(b)情形之间,其顶部变形趋势与常数型地基系数变化一致,但结构变形都小于常数型地基系数下结构的变形。其变形最大值与整体变形差距较小,且在结构底部达到最小值,与直线型的差距不明显,也就是说这种假设情况的计算,可能处于常数型和直线型之间,与两者都有一定的相似度。
3.4 其他模型
(1)具体计算方法。①相对刚度较大,视地基反力为线性分布,并作为荷载作用于底板,用变形法求解。②相对刚度较小,视为的弹性地基上闭合。结构:先用力法进行结构分离,然后分别用变形法和弹性地基梁求解。
(2)地基反力分布假設。①反力按直线分布;中间大两侧小和两侧大中间小。②反力强度与各点地基沉降量成正比分布。③地基为半无限弹性体,按弹性理论计算反力。
在本文所采用的荷载结构法中影响结构变形的因素不仅仅是地基系数,同样还有基地弹性反力、弹簧刚度、弹簧长度、弹簧的分布等其他相关因素都可以改变结构的变形。由于论文篇幅的原因再次不加以详细描述。
4结论与展望
4.1 结论
(1)荷载结构法就是将围岩和结构分开考虑。在荷载结构法中,周边岩土体向结构施加各种主动荷载,且岩土体对结构有一定的弹性抗力以约束结构变形,弹性抗力在计算中模拟为弹簧。由于荷载结构法相对来讲设计思路清晰,计算简洁,甚至有些计算可以不运用计算软件,所以它是目前设计人员常用的设计方法。
(2)通过计算发现在地基系数中,“常数”值法在结构变形的情况中,如果从安全的角度,确保结构的变形不足以影响施工进程与周围环境的情况的时候,可以假设地基系数为“常数”的计算方法进行计算。
(3)整个计算的过程和三个计算结果与多个实际工程结构变形的情况对比,发现二次元系数值法的计算结果与实际变形情况相似度更高,表明二次元系数值法灵活的适用于地层地基系数多变的情况下,也就因此二次元系数值法具有广泛的适应性。
(4)通过计算结果在图中的对比,发现线性函数系数值法的变化趋势,以及最值处于常数值系数法和二次元系数值法之间,与两者的变化趋势都有一定的相似度,所以在设计结构的时候,假设地基系数这样分布可以进行更经济的结构设计。
4.2 展望
荷载结构法由于计算简便,受地层参数浮动变化的影响不是很大,结构设计常采用。本文重点研究了在不同地基系数下的结构变形以及内力,并得到了一些结论,但仍有问题有待解决和改进:
(1)以更科学和更具有代表性的经验来完善经验类比法的内容,切忌按照传统经验闭门造车。未来的研究方向可以在如何尽情地利用围岩的承载能力上发展,从而使施工设计更加环保经济安全。
(2)根据实际情况以最科学的方法选用合理恰当的计算方法,而不是单纯的以计算简便为主。这样可以把计算结果更精确化稳定化。
参考文献
[1] TB 10003-2005.铁路隧道设计规范[S].北京:中国铁道出版社,2006年.
[2] 施仲衡.地下铁路设计与施工[M].西安:陕西科学技术出版社,2006:39.
作者简介
梅新(1987-),男,湖北安陆人;学历:硕士研究生,工程师,现就职单位:中铁第四勘察设计院集团有限公司,研究方向:从事地铁监测工作。
