HTS-A高强度钢疲劳裂纹扩展寿命研究
2020-04-20
(中国舰船研究设计中心,湖北 武汉 430064)
0 引言
高强度钢有着良好的综合力学性能,是目前工业中应用极为广泛的金属材料,如船舶行业、航空航天行业、压力器等。但是高强度钢有一个共性问题就是材料承载应力水平高而韧性不足[1]。为综合考虑高强度、高韧性、良好的可焊性和抗爆性等力学性能,高强度钢的屈服强度与强度极限的比值已接近甚至超过0.9[2]。具体到HTS-A钢材,其具有较高的屈服强度,但随之提高的屈强比使其塑性性能降低且易于产生应力集中,导致结构的安全裕度下降;而较低的相对疲劳强度和断裂韧度则使抵抗裂纹产生和扩展的能力降低,导致结构易于产生疲劳损伤[3],因此基于HTS-A钢建造的焊接构件的疲劳问题不可忽视。
在工程上,对含缺陷的结构,确保在安全的前提下,结构的剩余寿命是多少。可以根据材料的疲劳裂纹扩展性能来估算含缺陷的结构的剩余寿命,然而目前对高强度的疲劳裂纹扩展的研究仍不够完善[4]。
NASGRO损伤容限分析软件是NASA、FAA、ESA等机构进行飞行器疲劳分析的标准程序,其能够模拟金属结构的疲劳裂纹起裂、扩展和断裂,可以方便快捷地分析疲劳裂纹的扩展问题。NAGRO软件中分析裂纹扩展所采用的裂纹扩展速率模型为NASGRO公式[5],NASGRO公式综合考虑了应力比R、裂纹闭合效应f、应力强度因子幅值的阈值ΔKth、断裂韧度KC等方面对裂纹扩展的影响,因此获得了广泛的应用[6-8]。
本文先阐述了HTS-A钢平板试件弯曲循环载荷疲劳试验,获得试件的疲劳裂纹扩展寿命。然后基于试验数据,采用NASGRO软件分析研究HTS-A钢裂纹扩展问题,提出NASGRO软件计算HTS-A钢裂纹扩展寿命所需的经验参数和建议选取的断裂失效判据,实现用NASGRO软件高效估算HTS-A钢结构的裂纹扩展寿命。最后用文献[9]中单轴疲劳试验试件的裂纹扩展性能进一步验证该经验参数和断裂失效判据的合理性,为工程上解决HTS-A钢结构的裂纹扩展问题提供参考,有一定的工程应用价值。
1 平板试件疲劳试验
为研究HTS-A钢的低周疲劳特性,采用HTS-A钢制成平板试件,开展平板试件弯曲循环载荷作用的疲劳试验。
1.1 平板试件
采用厚度t=34 mm的大钢板对接焊后再切割成试件,这样处理是为了避免小试件焊接起点和终点的不均匀对试验结果所造成的影响。平板试件样式如图1所示,其中定义x轴沿着平板长度方向为纵向,y轴沿着板厚方向为横向,z轴沿着板宽方向为周向。
1.2 试验载荷
试验中采用加载频率为2.30 Hz的正弦波加载,如图1所示,通过四点弯曲横向加载实现弯曲循环应力,应力比R=0.1,试件的载荷按表1确定。
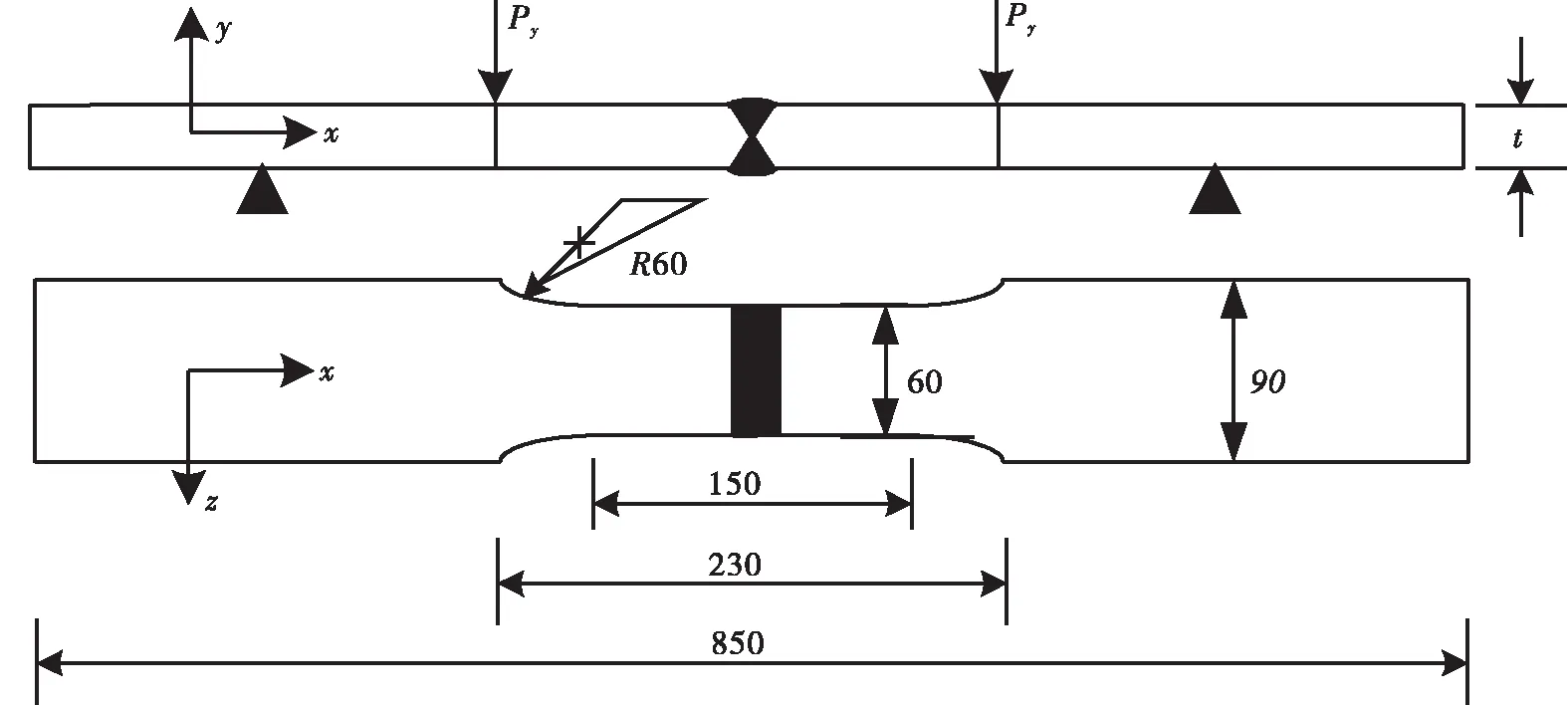
图1 平板试件示意图

表1 试件载荷
1.3 试验结果
试件从开始加载到最终断裂所承受的弯曲循环载荷的总次数称为试件的总寿命。试件的总寿命分为裂纹萌生寿命和裂纹扩展寿命[10]。在该次试验中,将裂纹深度小于0.5 mm的循环寿命称为裂纹萌生寿命,裂纹深度从0.5 mm扩展至试件断裂时的寿命称为裂纹扩展寿命。试件的疲劳寿命如表2所示。

表2 疲劳试验结果
由于焊接工艺、试件安装等对试验结果的影响,无论是裂纹扩展寿命还是萌生寿命,都有一定的离散性,这是符合实际的。
2 NASGRO裂纹扩展寿命研究
2.1 NASGRO公式
NASGRO损伤容限分析软件中计算疲劳裂纹的扩展寿命所采用的裂纹扩展速率模型是NASGRO公式,该表达式为[5]
(1)
其中,f是Newman裂纹闭合公式,用于分析裂纹尖端塑性变形导致的裂纹闭合效应,该表达式为:
(2)
各参数如下:
(3)
A1=(0.315-0.071α)Smax/σ0
(4)
A2=1-A0-A1-A3
(5)
A3=2A0+A1-1
(6)
式中:
a——裂纹尺寸,单位mm;
C、m、p、q——与材料有关的参数;


R——应力比;
α——平面应力/应变约束因子;
Smax——最大作用应力;
σ0——流变应力,是材料屈服极限σys与抗拉极限σb的平均值,即σ0=(σys+σb)/2。
从NASGRO公式可知,为获得结构在确定循环载荷下的疲劳裂纹扩展寿命,必须确定各式中的参数。
2.2 材料参数
2.2.1 基本参数
HTS-A钢的屈服极限σys=785 MPa,抗拉极限σb=845 MPa。
2.2.2 疲劳裂纹扩展参数C、m
疲劳裂纹扩展参数C、m的取值直接影响着结构疲劳裂纹扩展寿命计算结果的可靠程度,这两个材料参数可通过疲劳试验获得,HTS-A钢及其配套焊材的裂纹扩展参数C=2.306 8e-14、m=3.340 1。
2.2.3 疲劳裂纹闭合
对HTS-A钢材料的疲劳裂纹闭合效应,分别从以下两种情况进行分析:
1)情况一:考虑裂纹闭合效应。
由式(2)-(6)可知,若考虑裂纹的闭合效应,为保证疲劳裂纹扩展拟合曲线与疲劳试验数据的一致性,需要确定特定材料的平面应力/应变约束系数α和最大应力与流变应力的比值Smax/σ0。NASGRO中的大多数材料在参数拟合时对这两个参数均取常值。
平面应力/应变约束系数α的取值范围是从1(对应平面应力)到3(对应平面应变)。对于韧性好的材料的KIC/σys比值较高,则赋予相对较小的α值(1.5-2.0);而对于如高强度钢材料的KIC/σys比值相当低,则需要赋予相对较高的α值(2.5或更高)。因此对HTS-A钢的平面应力/应变约束系数α值取2.5。
最大应力与流变应力的比值Smax/σ0=0.3,该值接近各种标准试样疲劳裂纹扩展试验的平均值,因此在NASGRO中对大多数材料,如HY80、HY130等,在参数拟合时均采用了Smax/σ0=0.3。本文中对HTS-A钢的参数拟合时Smax/σ0也取0.3。
2)情况二:不考虑裂纹闭合效应。
计算疲劳裂纹扩展寿命时若不考虑裂纹闭合效应,即当应力比R为正时,使得裂纹张开公式f=R,因此可取α=5.845,Smax/σ0=1.0或在计算裂纹扩展寿命时,直接关闭裂纹闭合效应选项。
2.2.4 断裂韧度
对于SC30半椭圆表面裂纹模型,公式(1)中的KC设定为NASGRO材料数据库中的常数KIe,断裂韧度值KIe可按下式估算:
KIe=KIC(1+CkKIC/σys)
(7)
其中Ck=0.19842,当KIC/σys较大时,式(7)的计算结果非常大,因此在NASGRO材料库中KIe的值限定在KIC的1.4倍以内。

2.2.5 应力强度因子幅值的阈值
公式(1)中应力强度因子幅值的阈值ΔKth可由以下经验公式估算:
(8a)
(8b)
其中,
(9)
式中:
f[R]——Newman裂纹闭合公式(2);
A0——公式(3)中的常数;
ΔK1——应力比R→1时材料的应力强度因子幅值的阈值;
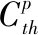
a0——内在小裂纹尺寸,典型值取0.0381 mm。
在NASGRO中,按式(8a)、(8b)计算应力强度因子幅值的阈值时,Newman闭合公式f及A0所采用的拟合参数为常见的平均值α=2.0,Smax/σ0=0.3。对于HTS-A钢的参数拟合,也取α=2.0,Smax/σ0=0.3。
分析式(8a)、(8b)可知,若将Cth设定为0,则相当于用一个较低的阈值,较低的阈值使得疲劳裂纹扩展加快,从而使得疲劳裂纹扩展寿命的预测结果相对保守。而当Cth取非零值时,相当于用一个较高的阈值,这会使得计算结果不够保守。为此,为获得一个相对保守的预测寿命,计算HTS-A钢的裂纹扩展寿命时,对整个计算过程中,均取Cth=0。
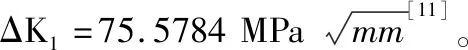
2.3 失效判据
在NASGRO中提供多种结构断裂失效判据,在分析HTS-A钢的疲劳特性时,主要用以下三种判据进行分析。
1)对于SC30半椭圆表面裂纹,当裂纹长短轴的a和c处的最大应力强度因子Kmax超过断裂韧度KIe时,则认定裂纹失稳,结构失效。以下称为KIe判据。
2)当净截面的平均应力Sn超过材料的流变应力σ0,则认定为结构失效。以下称为Sn判据。净截面应力计算公式如下:
(10)
式中:An——净截面面积;
P——合力;
M——合力矩;
c——净截面韧带两侧间距;
In——净截面的惯性矩。
3)当SC30半椭圆表面裂纹深度a和半长c扩展到指定的极限值,则认定结构失效。以下称为临界裂纹尺寸判据。
2.4 NASGRO裂纹扩展寿命分析
在以上分析中,初步确定了HTS-A钢的材料参数,但还需进一步验证这些参数的有效性。在以上材料参数中,难以确定的是对于HTS-A钢的疲劳裂纹扩展情况是否考虑裂纹的闭合效应,以及结构断裂失效的判据的选择。为此在开启KIe判据的前提下,分别计算了以下四种情况的试件的裂纹扩展寿命:①考虑裂纹闭合效应,采用Sn判据。②考虑裂纹闭合效应,采用临界裂纹尺寸判据。③不考虑裂纹闭合效应,采用Sn判据。④不考虑裂纹闭合效应,采用临界裂纹尺寸判据。经分析平板试件弯曲载荷疲劳试验的试验结果,发现当裂纹深度a大于15 mm时,裂纹迅速扩展导致试件断裂,因此对该次试验,临界裂纹尺寸取ac=15 mm,cc=30 mm。
2.4.1 考虑裂纹闭合效应
对受弯曲载荷作用的HTS-A钢试件,考虑裂纹闭合效应,NASGRO计算裂纹扩展寿命结果如表3所示。

表3 NASGRO计算结果
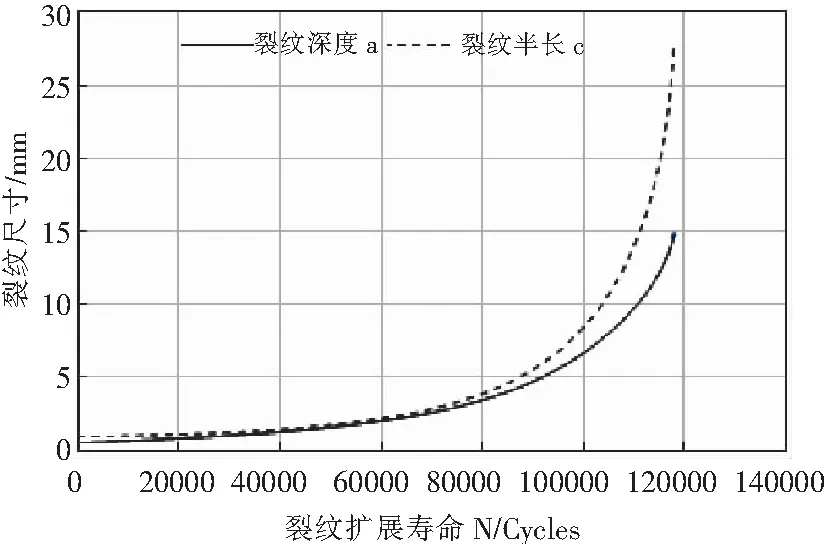
图2 考虑裂纹闭合效应时裂纹尺寸的变化曲线图
从表3可知,考虑裂纹闭合效应,采用Sn判据试件断裂失效时的裂纹深度a和半长c的值要比采用临界裂纹尺寸判据的a和c要小,因此采用Sn判据所得裂纹扩展寿命比采用临界裂纹尺寸判据所得寿命小1 976次。考虑裂纹闭合效应,从图2可以看出,当裂纹尺寸扩展至Sn判据的极限裂纹尺寸a=12.81,c=21.27时,裂纹扩展已进入高速扩展阶段,裂纹将快速扩展引起结构失效。因此采用Sn判据和临界裂纹尺寸判据,所得结果相差甚小。
平板试件弯曲载荷疲劳试验裂纹扩展结果和NASGRO计算裂纹扩展寿命结果如表4所示。

表4 NASGRO计算结果与试验结果对比
从表4可知,用NASGRO计算裂纹的扩展寿命,考虑裂纹闭合效应,无论是采用Sn判据,还是采用临界裂纹尺寸判据,所得结果是试验结果的1.6~2.3倍。显然,计算HTS-A钢的裂纹扩展寿命,若考虑裂纹闭合效应,所得结果是不合理的,因此不宜考虑裂纹闭合效应。
2.4.2 不考虑裂纹闭合效应
对受弯曲载荷作用的HTS-A钢试件,不考虑裂纹闭合效应,NASGRO计算裂纹扩展寿命结果如表5所示。

表5 NASGRO计算结果
从表5可知,不考虑裂纹闭合效应,采用Sn判据试件断裂失效时的裂纹深度a和半长c的值要比采用临界裂纹尺寸判据的a和c要小,因此采用Sn判据所得裂纹扩展寿命比采用临界裂纹尺寸判据所得寿命小908次。不考虑裂纹闭合效应,从图3可以看出当裂纹尺寸扩展至Sn判据的极限裂纹尺寸a=12.78 mm,c=21.20 mm时,裂纹扩展已进入高速扩展阶段,裂纹将快速扩展引起结构失效。因此采用Sn判据和临界裂纹尺寸判据,所得结果相差甚小。
平板试件弯曲载荷疲劳试验裂纹扩展结果和NASGRO计算裂纹扩展寿命结果如表6所示。

图3 不考虑裂纹闭合效应时裂纹尺寸的变化曲线图
从表6可知,用NASGRO计算裂纹的扩展寿命,不考虑裂纹闭合效应,无论是采用Sn判据,还是采用临界裂纹尺寸判据,都得到与试验结果较为吻合的计算结果,除了与试件No.1-1的试验结果相对误差超过20%外,其余两个试件的NASGRO计算结果与试验结果的最大相对误差仅为2.13%。
从以上分析可知,NASGRO计算HTS-A钢的裂纹扩展寿命,不考虑裂纹闭合效应所得结果令人满意,是合理的。此外,在工程上,为保证结构的安全性,对裂纹的临界尺寸的要求会更小,对此所求得的裂纹扩展寿命会更保守,因此对于断裂失效的判据的选择,KIe判据、Sn判据、临界裂纹尺寸判据都是合理的,建议在计算时同时开启三种断裂判据,选择更为保守计算结果。

表6 NASGRO计算结果与试验结果对比
2.4.3 NASGRO裂纹扩展结果
由以上数据的对比分析可知,使用NASGRO计算受弯曲载荷作用的HTS-A钢试件的疲劳裂纹扩展寿命时,不考虑裂纹闭合效应所得计算结果最为合理。以下给出不考虑裂纹闭合效应,采用Sn判据的裂纹扩展情况如图4所示。
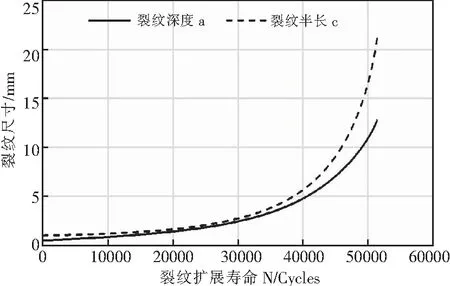
图4 采用Sn判据,裂纹尺寸随载荷加载次数的变化
2.5 经验参数
由以上分析,确定了NASGRO计算HTS-A钢裂纹扩展寿命的经验参数,如表7所示。
表7中第一组α=5.845,Smax/σ0=0.1是为了不考虑裂纹闭合效应,也可以在NASGO中直接关闭裂纹闭合效应选项。第二组α=2.0,Smax/σ0=0.3为了确定公式(1)中应力强度因子幅值的阈值ΔKth。
3 算例验证
采用NASGRO软件使用以上提出的经验参数和开启三种断裂失效判据计算文献[9]中的单轴疲劳试验试件的裂纹扩展寿命,并将所得结果与试验结果进行对比分析。
3.1 试验情况
文献[9]中的单轴疲劳试验采用厚度为35 mm的钢材制成如图5所示的平板对接试件。试验中采用三点弯曲加载实现弯曲循环载荷。载荷的大小Py=75 KN,所产生的弯曲正应力σm=658.2 MPa,应力比R=0.1。

表7 经验参数
3.2 结果分析
文献[9]中裂纹深度的临界值为ac=10 mm,因此对临界裂纹尺寸判据取ac=10 mm,cc=30 mm。NASGRO计算试件的裂纹扩展寿命结果与文献[9]中单轴疲劳疲劳试验裂纹扩展寿命结果如表8所示。
从表8可以看出,NASGRO计算试件的裂纹扩展寿命,裂纹扩展尺寸先达到临界裂纹尺寸,致使计算结束。当裂纹尺寸达到临界裂纹尺寸时,NASRO计算结果与试验结果非常接近,最大相对误差仅为3.08%,且所得结果只比No.1-3试验结果大,比其他两组试验结果小,所得结果更为吻合。图6为采用临界裂纹尺寸判据计算裂纹扩展寿命的裂纹尺寸变化情况,可以看到当裂纹深度a扩展至10 mm时,裂纹的扩展速率相当快,裂纹将快速失稳。再来分析采用Sn判据的计算结果,发现所得结果相对误差大些,但也在6%以内,因此,也是较为吻合的。

表8 NASGRO计算结果与文献[9]中试验结果对比
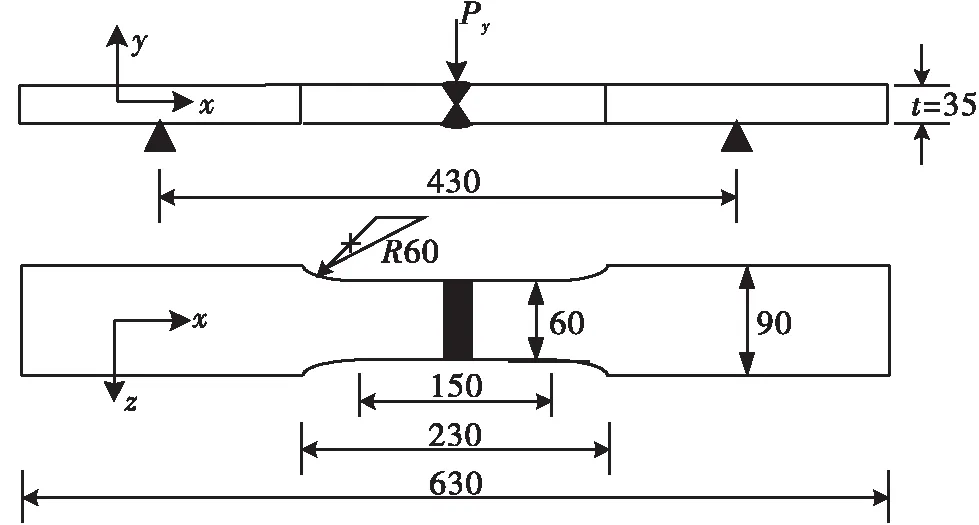
图5 文献[9]中平板试件示意图
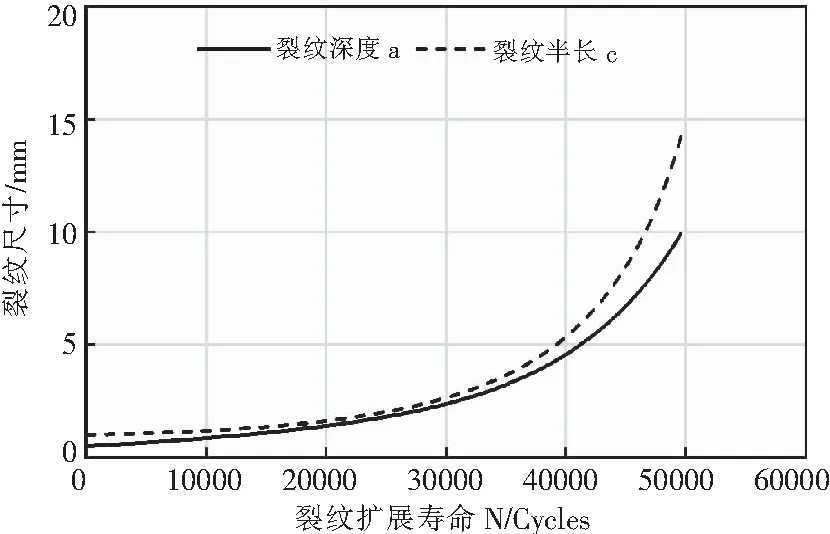
图6 NASGRO中试件的裂纹尺寸的变化曲线图
总的来说,NASGRO计算结果还是挺满意的,再次验证了所提出的经验参数的有效性。
4 结语
本文基于NASGRO损伤容限分析软件分析研究了HTS-A钢的裂纹扩展问题,提出了NASGRO软件仿真计算10CrNi5MoV钢疲劳裂纹扩展寿命的经验参数和分析了断裂失效判据的选择。并且与文献[9]中的试验结果进一步对比分析,发现采用临界裂纹尺寸判据,所得结果最大误差仅为3.08%,而采用Sn判据所得结果也在6%以内,获得了较为满意的结果,说明使用该经验参数计算HTS-A钢的裂纹扩展寿命是较为合理的,实现了用NASGRO高效估算HTS-A钢结构的疲劳裂纹扩展寿命。而对于断裂失效判据的选择,这个应该视工程实际应用而定,建议是选择较为保守的预测寿命,这为工程上HTS-A钢结构的裂纹扩展和剩余寿命估算提供参考。
