AP多粒度级配固体推进剂非稳态燃烧响应模型

2020-04-20金秉宁刘佩进徐冠宇

含能材料 2020年4期

金秉宁，刘佩进，徐冠宇

（西北工业大学燃烧、热结构与内流场重点实验室，陕西西安 710072）

1 引言

固体推进剂燃烧响应是燃烧不稳定的主要影响因素。近年来，从全尺寸发动机研制过程中发现，同样的装药结构，推进剂配方的微小变化、原材料批次以及工艺等因素均会导致推进剂燃烧响应特性的变化，产生燃烧不稳定问题。由于缺乏对燃烧响应机理的深入认识，发动机研制中往往采用“改配方-测量-再改配方-再测量”的方法，降低推进剂燃烧响应的增益作用。但这种研究方法效率低、周期长、实验次数多、难以快速准确地提出合理解决方案，从而给研制者们带来极大的困难。因此，十分有必要开展实际配方组分对固体推进剂燃烧响应影响规律的理论研究，为发动机研制提供有力的理论支撑和改进依据。

固体推进剂燃烧响应理论的研究需从稳态燃烧特性和非稳态燃烧特性［1-2］两个方面开展。国外开展了大量研究。其中，Culick［3-5］建立了均质推进剂一维准稳态气相燃烧模型（QSHOD模型），并将高氯酸铵（AP）燃烧模型带到参数A和B中进行修正，获得AP粒度对响应函数的影响。Rasmussen等［6］以一维多火焰稳态燃烧模型（BDP）［7］为基础，建立了一维复合推进剂压强耦合响应模型，获得了AP含量、粒度以及工作压强等参数对燃烧响应特性的影响，加深了研究者们对非均质推进剂燃烧响应特性的认识。Glick等［8］在燃烧过程中考虑了多元、多级配氧化剂的组成，建立了“小系统综合（PEM）”稳态燃烧模型。Cai等［9-10］建立了二维三明治模型，获得了AP粒径、压强对燃速和火焰高度的影响以及瞬态压强振荡之后推进剂的火焰结构和燃烧响应特性。Jackson 等［11］采用“Random Pack”模型，对复合推进剂进行了三维数值模拟，获得了多级配AP复合推进剂的压强耦合响应函数。但该模型需要的计算资源较大，计算时间较长。Renie和Osborn［12］基于小扰动理论，分析了氧化剂颗粒大小、燃烧室压强和平均流速对燃烧响应函数的影响。国内主要开展了稳态燃烧模型方面的研究。其中，周志清等［13］采用多步化学反应动力学机制，建立了三明治二维细观燃烧模型。赵瑜基于详细化学动力学机制，建立了复合推进剂燃烧模型［14］。张炜等建立了AP/黑索今（RDX）两种氧化剂含量和粒度级配可任意变化的AP/RDX/端羟基聚丁二烯（HTPB）推进剂稳态燃烧模型［15］。彭培根等基于以往复合推进剂燃烧模型和大量实验现象提出了一个AP/RDX推进剂的复合多火焰燃烧模型［16］。刘佩进等从燃烧学、声学和动力学出发，对复合推进剂的压强耦合响应开展了理论、实验和数值计算研究［17］，对复合推进剂的燃烧响应特性有了较全面的认识。

综上所述，国外对于均质和非均质推进剂燃烧响应模型开展了大量的研究，但关于非匀质推进剂中氧化剂粒度级配及配比对响应函数影响的研究较少；国内对于均质和非均质推进剂的稳态燃烧模型开展了大量的研究，而燃烧响应模型则研究较少，关于推进剂配方组分对响应函数影响的认识大多是基于实验测量结果，对燃烧响应机理缺少深入的认识，使得工程研制中较难提出降低推进剂压强耦合响应函数的抑制方法。

为此，本研究以BDP多火焰燃烧模型为框架，考虑实际推进剂中AP多级配粒度分布，建立AP多粒度级配的AP/HTPB推进剂燃烧响应模型，对模型进行校验。并针对几种常用的AP粒度，在不同粒度级配和配比条件下开展非稳态计算，深入分析AP粒度、级配和配比等参数变化对压强耦合响应函数的影响规律。

2 AP多粒度级配燃烧响应模型

BDP多火焰模型假设复合推进剂仅由单一粒径AP和 HTPB粘合剂组成［4，6］，属于双组元推进剂。模型包含AP分解焰、扩散火焰和初焰的多火焰结构。AP分解焰为AP分解产物NH3与HClO4的反应，产生于AP“气柱”中，向燃面反馈热量，属于预混火焰。初焰为AP分解产物与粘合剂热解产物之间的化学反应，受扩散和化学反应速率影响，属于扩散火焰。终焰为粘合剂热解产物和AP焰富氧产物间的反应，位于AP分解焰外端，属于扩散火焰。与AP分解焰是相连，并向燃面反馈热量。该模型的主要假设如下：

（1）沿垂直燃烧表面方向视为一维；

（2）AP和粘合剂表面分解反应符合Arrhenius定律；

（3）AP和粘合剂具有不同的表面温度；

（4）气相反应为简单均相反应，且产物为完全气体。

2.1 AP多级配模型构建

对于AP多级配推进剂来说，可将AP多粒度级配AP/HTPB复合推进剂视为由多个假定AP单粒度AP/HTPB系统组合而成［18］，假设AP表面的单元火焰是相互独立燃烧，并将推进剂重新排列成多组各包含一种AP粒度的假想单级配推进剂（如图1所示）。这里考虑的AP四级配推进剂，其中AP粒度分别为Ⅰ类、Ⅱ类、Ⅲ类和细AP。

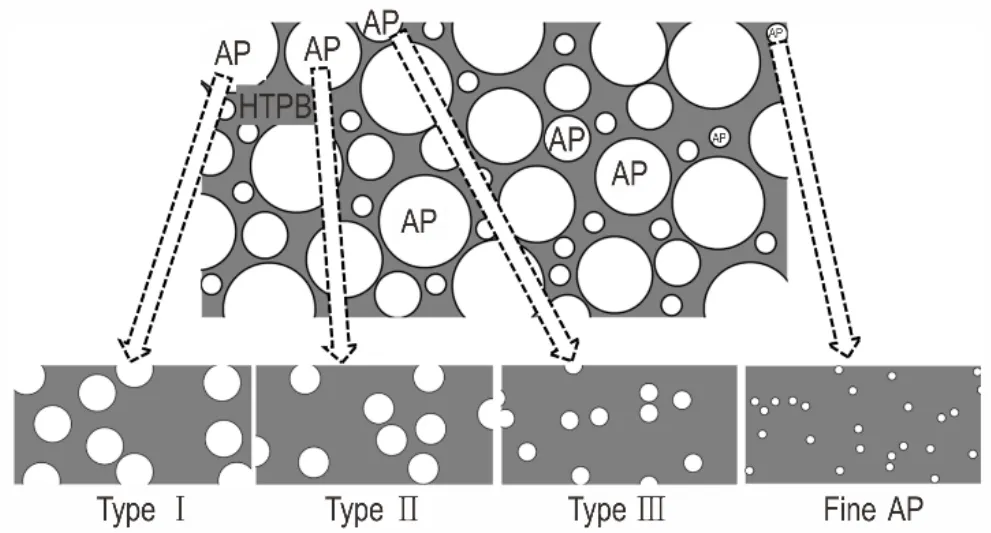
图1 AP四级配假想推进剂模型Fig.1 The sketch of Quadruplemodal propellant model

重新排列的AP单级配假想推进剂火焰构型满足BDP多火焰模型，其中，AP分解火焰和扩散终焰受AP粒度尺寸影响较大，需要根据不同AP粒度尺寸条件分别计算，图2所示为相邻两个不同AP粒径的火焰模型示意图。

从图2可以看出，相邻的两个AP粒子，由于粒度不同，相应的分解焰xf，AP，xr和终焰 xf各不相同，并且AP表面温度Ts，AP和热反馈量QL也各不相同。因此，多级配模型中的火焰个数取决于AP粒径种类数量，如果是AP四级配，则有四个不同尺寸的四个 AP分解焰xf，AP，n、四个 AP 表面温度Ts，AP，n；对于粘合剂，为了简化计算，其表面温度按照小尺寸AP颗粒周围的粘合剂温度计算；多级配推进剂的燃烧速率由各个单级配的结果按照其AP质量含量比例所占权重综合统计计算，且模型中各组分的质量通量由AP单级配BDP火焰模型决定。

2.1.1 稳态燃烧模型

根据实际推进剂配方AP粒度分布，改进模型中Ⅰ类 AP 平均粒径为DAP，1，含量为α1；Ⅱ类 AP 平均粒径DAP，2，含量α2；Ⅲ类 AP 平均粒径DAP，3，含量为α3；细粒度 AP平均粒径DAP，4，含量为α4；αAP为 AP总含量，如公式（1）所示，而HTPB含量为1-αAP。

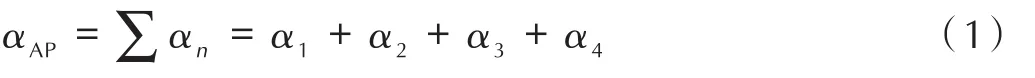
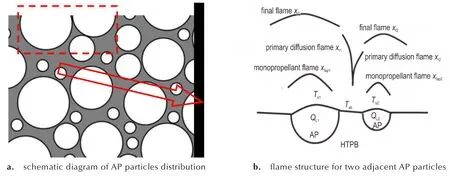
图2 相邻两个不同AP粒径的火焰模型示意图Fig.2 The proposed flame structure for two adjacent AP particles

根据文献［6］中AP单级配推进剂质量通量的表达式，AP多级配推进剂中每种AP单级配推进剂的质量通量Gp，n和多级配推进剂总质量通量Gp可表示如下：

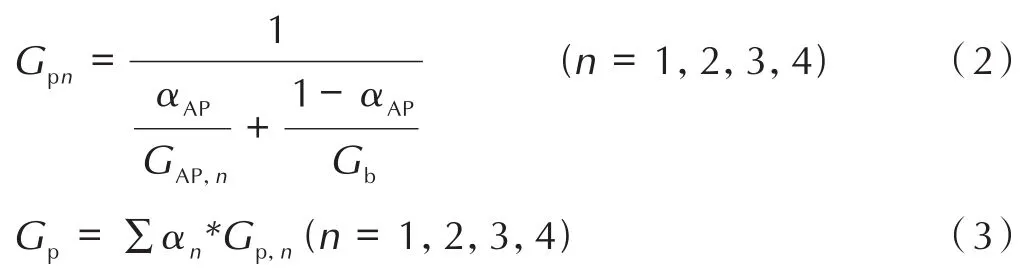
式中，αAP为 AP（氧化剂）含量，n则代表AP级配数，GAP，n为各个粒度的氧化剂质量生成速率，Gb为粘合剂的质量生成速率，其表达式如下［6］：

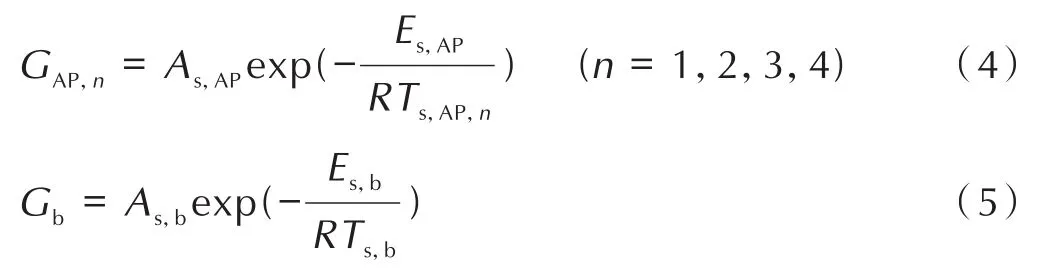
式中，在多级配模型中，不同AP粒子具有不同表面温度Ts，AP，n，其表达式如下所示［6］：

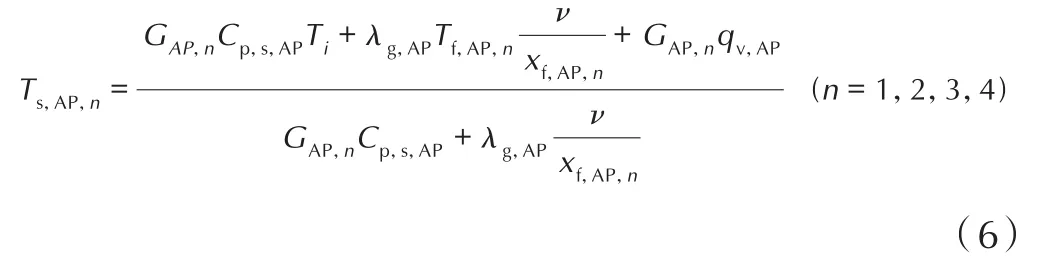
而粘合剂温度采用统一值Ts，b，取最小尺寸AP颗粒周围的粘合剂温度［6］：

相应的 AP 多级配的 AP 分解焰火焰温度Tf，AP，n、AP 分解焰火焰高度xf，AP，n，初始扩散火焰高度xr，n，扩散终焰高度xf，n均与单级配模型表达式相一致，与AP等效粒径有关，其各个级配AP等效粒径的表达式如下［6］：

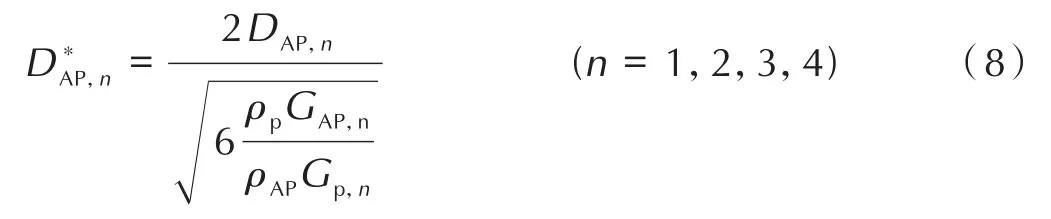
2.1.2 非稳态燃烧模型

AP多级配非稳态模型计算，基本上与AP单级配非稳态模型相同。当推进剂进行非稳态燃烧时，∂T/∂t≠0，此时模型中各个火焰的高度、温度等参数均会随时间变化，因此需要考虑AP和粘合剂表面能量方程中随时间变化的积分项。其非稳态条件下的AP和粘合剂表面温度［6］：

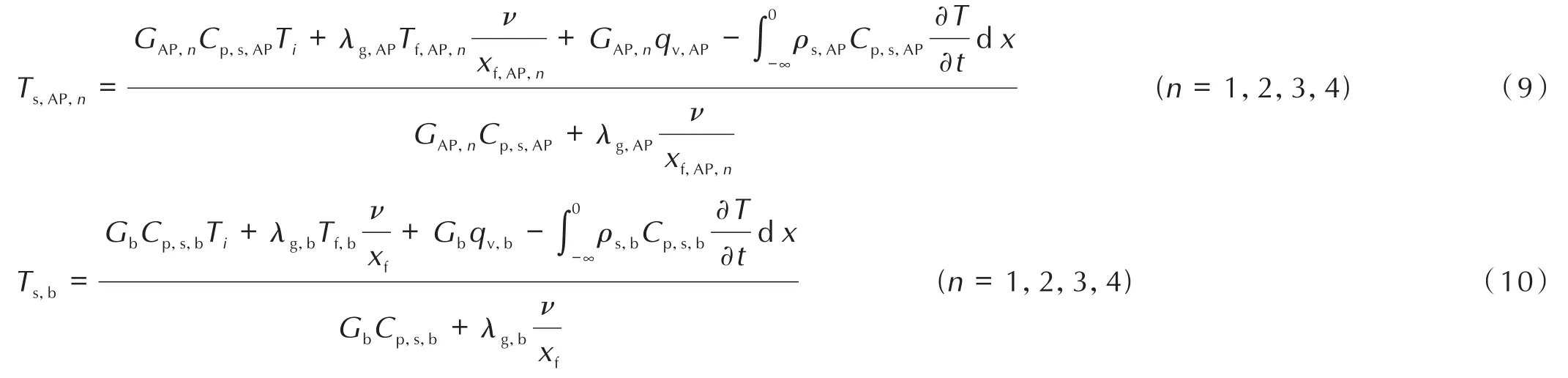
式中，多级配 AP 颗粒表面温度Ts，AP，n和粘合剂表面温度Ts，b须采用非稳态计算结果表征非稳态特性。而AP质量通量GAP，n、粘合剂质量通量Gb和推进剂总质量通量Gp是Ts，AP，n、Ts，b和（Ts，AP，n，Ts，b）的函数。关于xf，n、xr，n、xf，AP，n和Tf，AP，n的计算，则采用稳态计算结果进行插值计算出压强扰动条件下不同时刻压强所对应的值，作为已知参数来求解非线性方程组。

2.1.3 AP多级配燃烧响应函数构造

稳态和非稳态结果中包含了多个参变量，如Gp，n、GAP，n、Gb、Tf，n、Ts，AP，n、Ts，b、xf，n、xr，n、xf，AP，n，这些参数作为非稳态计算工况的初始参数，用来计算推进剂内部温度分布和不同时刻下各参数变化情况，并根据计算结果获得推进剂的压强耦合响应函数。压强耦合响应函数中的为压强波动与平均压强的比值，是模型初始参数给定的量；因此，构建响应函数的关键参数即通过模型获得燃速扰动量r′和平均量的比值。然而对于非稳态模型计算结果可以获得燃速扰动量r′，通过r′进行平均化处理方可得到燃速的平均量。燃速平均量的处理方法如下：

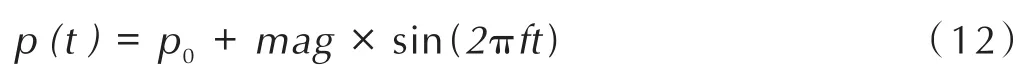
式中，p0为平衡压强；mag为扰动幅值（未特殊说明均采用平衡压强的20%）；f为扰动频率；t为燃烧时间。通过改变正弦压强波动函数的频率进行非稳态计算可以获得不同扰动频率下的燃速-时间曲线。

图3为平衡压强在10 MPa，振荡频率为175 Hz，振荡幅值为平衡压强的20%时的压强振荡时间曲线以及模型中所有参变量随时间振荡变化曲线，模型中AP总质量分数为80%，AP采用两种粒度（50/200 μm），质量配比为8∶1，表面温度为298 K。可以看出，随着压强振荡输入量的变化，模型中AP和粘合剂以及推进剂总质量通量随时间呈周期性的振荡变化，振荡频率与压强振荡频率相同。并且推进剂燃烧表面的温度也随压强振荡的变化呈正弦波动，波动频率与压强振荡频率相同。

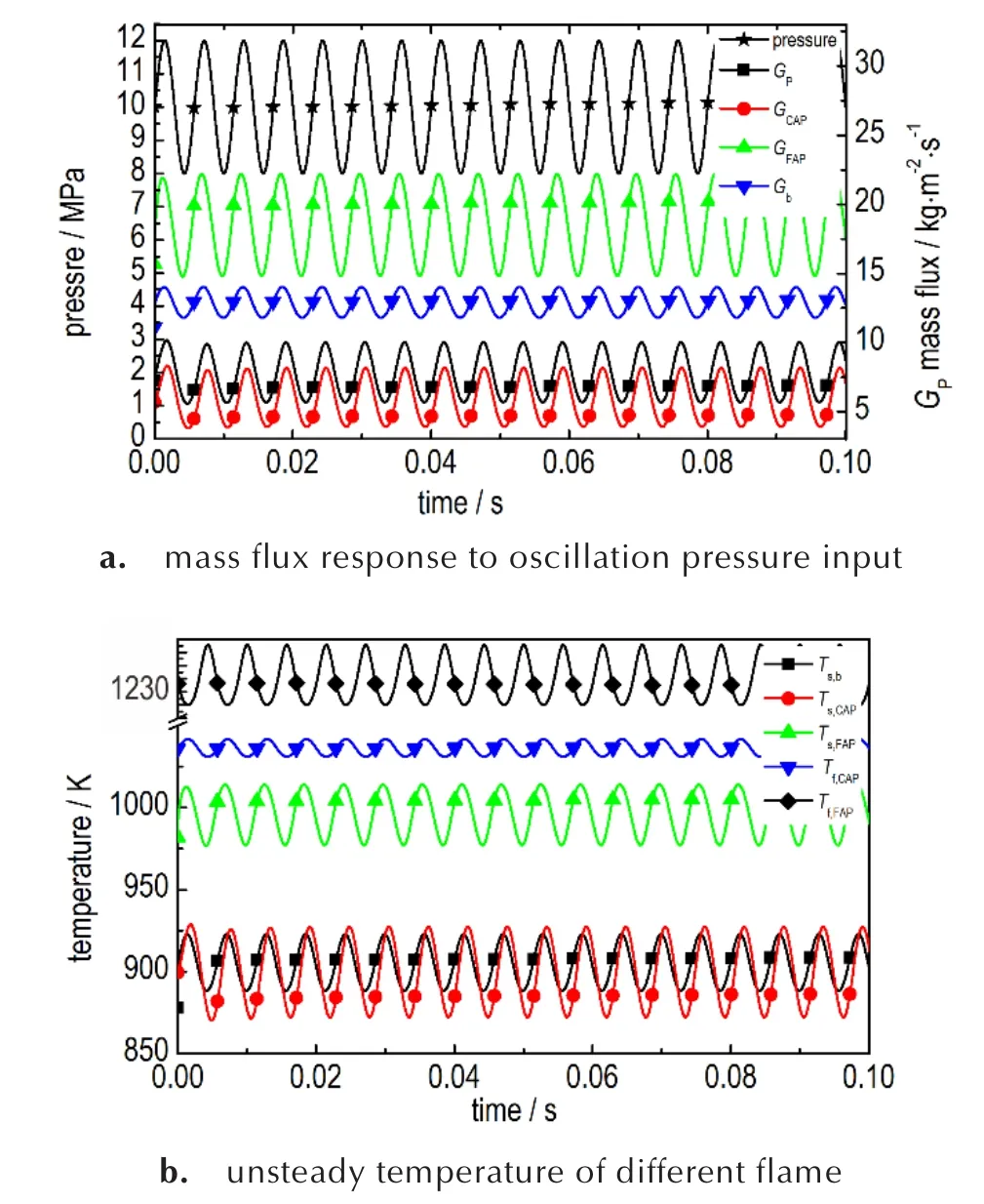
图3 振荡条件下模型参数振荡曲线Fig.3 Typical model parameters response to oscillation pressure input

AP多级配推进剂燃烧模型采用Matlab计算平台编程计算，与AP单级配模型基本上相同，均是分别求解稳态（公式（1）～（8））和非稳态（公式（9）～（11））的非线性方程组。然而，对于不同AP级配来说，其稳态和非稳态的非线性方程组的数量不同，级配越多，方程数量也越多，计算量也越大，计算时间更长。AP单级配燃烧响应模型计算的非线性方程数量是11个，而本文建立的AP四级配燃烧响应模型则由36个非线性方程组成。该模型仍是AP和HTPB双组元推进剂，其中AP质量分数为73%～87%，初始温度为298 K，计算压强2～20 MPa内均可以获得燃烧响应函数。

2.2 模型校验

2.2.1 稳态模型校验

针对建立的AP多组元AP/HTPB推进剂燃烧模型，首先根据国内外文献资料中的实验结果对稳态燃烧模型进行验证。分别采用文献［19］中相关的实验数据进行模型校验。其中AP粒度含量约为80%，AP级配分别为双级配、三级配和四级配，AP粒度分别采用400，200，90，50 μm和20 μm，基本涵盖了AP各种粒度分布。表1给出了具体的粒度级配和配比参数。

模型中用到的 AP 和 HTPB 的指前因子As，AP，As，b、活化能Es，AP，Es，b以及比热容cp，g，AP，cp，s，b等参数值详见文献［20］。模型计算结果和实验结果如图4所示。

由图4可知，在高压强条件下（＞5 MPa），多级配稳态燃烧模型的计算值与实验测量值之间的误差均小于10%，与实验测量结果吻合得较好。同时，从AP粒度配比的涵盖范围来看，包含了实际推进剂中采用的多种粒度分布，具有一定的通用性。因此，可以认为所建立的多级配多火焰稳态燃烧模型是可行的，能较好地反映推进剂配方参数变化的燃速特性，可以进行非稳态压强耦合响应函数的计算工作。

表1 推进剂配方参数及计算工况Table 1 Propellant formulations and detailed conditions for calculation

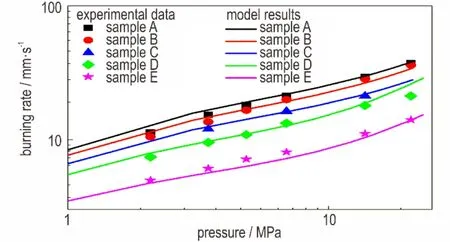
图4 5种AP多级配模型计算结果与实验结果比较Fig.4 A comparison of between the modeling results and the experimental data for five propellants

2.2.2 多级配响应函数验证

针对文献［21］中AP三级配AP/HTPB推进剂配方（表2），开展多级配响应函数计算，并与文献中实验结果进行对比，对多级配响应函数模型进行验证。文献采用脉冲触发T型燃烧器实验测量装置，实验测量工作压强约为6.9 MPa，测量频率为400～1300 Hz。因此，AP多级配推进剂响应函数模型的计算工作压强约为6.9 MPa，计算频率范围为200～1300 Hz，AP总含量为87.6%，HTPB含量为12.4%。计算结果如图5所示。

由图5可知，采用粒度分布为400/200/17 μm的AP三级配推进剂，其粒度配比分别为23.23∶34.98∶29.15，其响应函数计算结果与实验拟合结果在200～1300 Hz内，基本上吻合得较好，其中振荡频率为250～800 Hz内，响应函数值的误差在5%～9%；而振荡频率约为1200Hz时，模型计算结果与实验拟合结果（黑色虚线）的误差值相对较大，约为14%；但该模型计算结果仍在实验测量值（黑色方框□）的上下限范围内，因此认为模型计算的误差是可接受的。

表2 AP三级配推进剂配方参数［21］Table 2 Formulation of AP Triple modalpropellant［21］

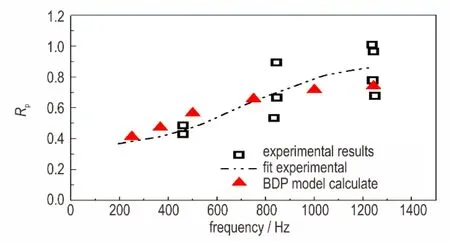
图5 计算模型与实验结果对比验证Fig.5 A comparison of the predicted and measured Rp values

通过与参考文献中［21］的实验测量值进行比较发现，AP多级配推进剂的压强耦合响应函数计算值与实验测量值之间的误差均小于14%，与实验测量结果吻合较好。可以认为，建立的多级配推进剂压强耦合响应函数计算模型是可行的，能较好地反映出AP多级配推进剂响应函数特性，可以开展AP多级配推进剂响应函数特性的计算研究。

3 计算结果及影响规律

根据实际推进剂中经常采用的四种AP颗粒粒度（330，250，110 μm 和 50 μm），通过调整各个粒子含量的配比关系，分别得到AP多粒度级配的AP/HTPB推进剂，通过模型开展稳态和非稳态计算，获得不同的级配和配比条件下各种粒度颗粒对响应函数特性的影响。模型中推进剂仍为双组元AP/HTPB复合推进剂，其中AP含量为80%，平衡工作压强为10 MPa，压强振荡幅值为平衡压强的20%，振荡频率为25～1000 Hz。

3.1 AP粒度配比对燃烧响应的影响规律

为获得 330，250，110，50 μm四种 AP粒度中某一粒度含量变化对响应函数影响，粒度配比变化规则为：AP总含量不变，一次只改变一种AP粒度的含量（a），相应其它三种粒度含量同时改变，计算结果如图6所示。

由图6可知，不同AP粒度主导变化对响应函数的变化规律有明显的不同。其中图6a中随着330 μm粒度AP含量的降低，中低频（＜250 Hz）时，含量从8∶1∶1∶1降低至1∶1∶1∶1时，响应函数值快速降低，其中峰值变化最大，从1.7降低至1.35，但峰值频率变化不大；而含量从1∶1∶1∶1降低至0.125∶1∶1∶1时，响应函数值基本变化不大。对于中高频来说（＞250 Hz），随着含量的降低，响应函数值增大；并且频率越大，响应函数值变化较大。

图6b中，250 μm粒度AP含量变化对响应函数的影响基本上与330 μm相同，响应函数变化仍在不同频率范围变化不同，即中低频范围内，随着a250含量降低，响应函数值下降，峰值变化从1.56降至1.34；在中高频范围内，随着a250含量降低，响应函数值上升。单临界频率约为400 μm，向高频移动。

图6c中，在整个频率范围内，随着a110含量降低，响应函数值均下降；但不同频率范围内下降的趋势不同，低频范围内变化趋势较为缓慢，而高频范围内变化趋势较快。并且随着响应函数值降低，响应函数峰值频率向低频移动。

图6d中，以含量1∶1∶1∶1为临界情况，当a110含量＞该临界条件时，在整个频率范围内，随着a110含量降低，响应函数呈整体型降低的趋势变化；而当a110含量＜临界条件时，随着a110含量降低，响应函数呈区域型变化，其中中低频范围内响应函数上升，而中高频范围内，响应函数下降。a110含量的降低，对于峰值频率向低频移动。

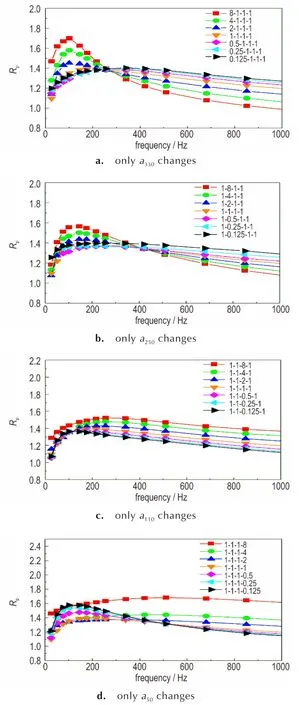
图6 AP四级配单粒度配比变化对响应函数影响（10 MPa）Fig.6 Effect of the change of particle content on response function in Quadruplemodal propellants（10 MPa）

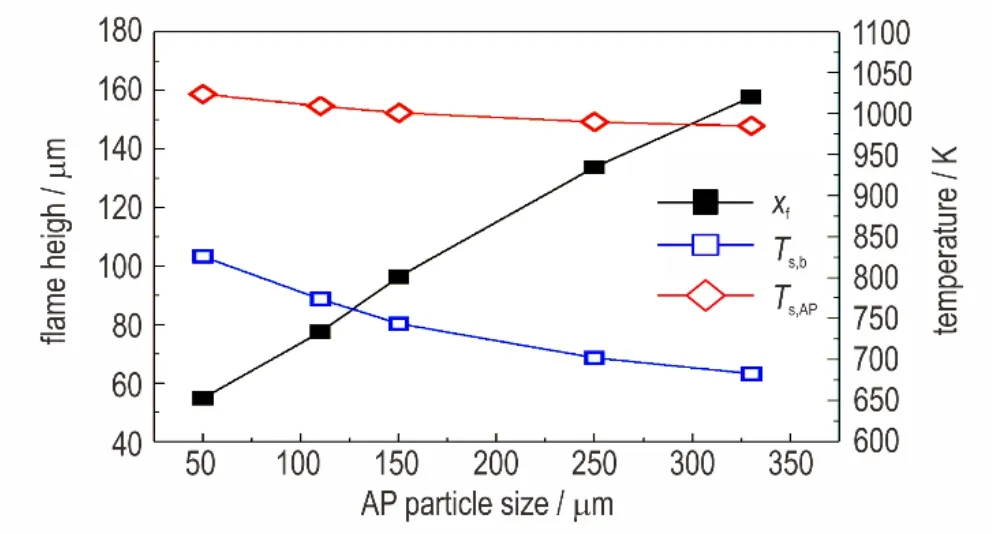
图7 扩散火焰高度与AP、粘合剂表面温度关系（10 MPa）Fig.7 Change of diffusion flame height and surface temperature of AP and the binder with particle size of AP（10 MPa）

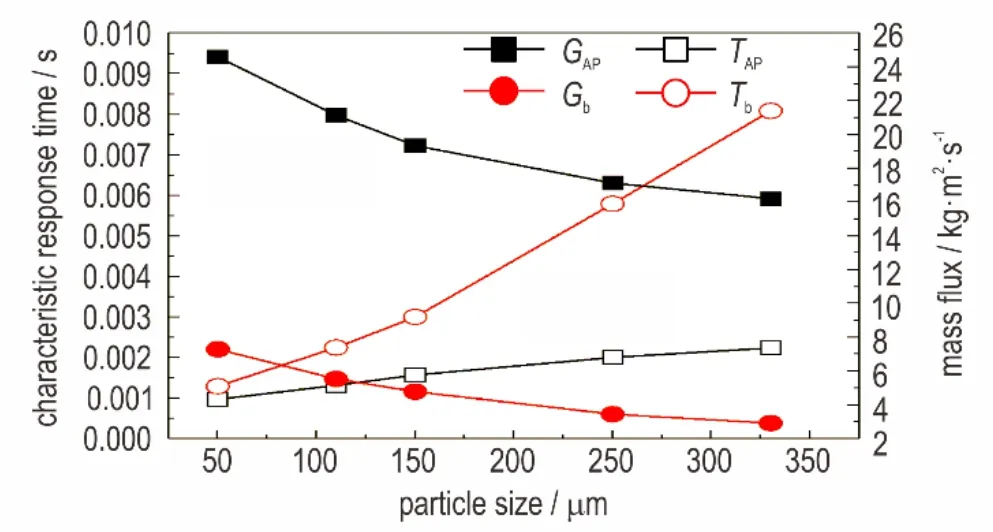
图8 AP和粘合剂的质量通量以及特征时间随AP粒度变化Fig.8 Change of mass flux and characteristic response time of AP and binder with particle size of AP

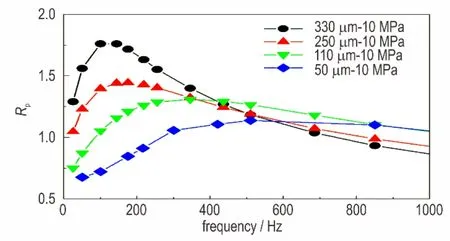
图9 四种AP粒度响应函数分布曲线Fig.9 Effect of the particle size of AP on Rp

3.2 AP粒度级配对燃烧响应的影响规律

针对双级配 110 μm/50 μm、250 μm/50 μm 和330 μm/50 μm三种不同AP粒度的双级配推进剂，采用粗细粒度配比为4∶1，分别用250 μm或者330 μm替代双级配中粗粒度AP的50%含量，而小粒度50 μm含量保持不变，形成三种AP三粒度级配推进剂，配比为2∶2∶1。AP粒度级配对响应函数结果如图10所示。

图10 AP粒度级配对响应函数的影响Fig.10 Effect of the AP modal on Rp

从图10可以看出，在110 μm/50 μmAP双级配推进剂中，当用 250 μm 或 330 μm AP替代 50% 的 110 μm AP含量时，响应函数在不同频率范围变化不同：小于200 Hz时，随着更大粒度的加入，响应函数增大；大于200 Hz时，则趋势相反。在 330 μm/50 μm AP双级配推进剂中，当用250 μm或者110 μm AP替代50%的330 μm，响应函数仍是在不同频率范围变化不同：小于200 Hz时，随着更大粒度的加入，响应函数快速降低：大于200 Hz时，趋势相反。对于AP粒度组合250 μm/50 μm 推进剂来说，当用 330 μm或者 110 μm AP替代50%的250 μm AP含量时，响应函数的变化趋势完全相反；用大于原有粗粒度AP替代时，响应函数变化规律与110 μm/50 μm AP双级配推进剂变化规律相同；而用小于原有粗粒度AP替代时，响应函数变化规律与330 μm/50 μm AP双级配推进剂结果变化规律相同。

因此，对于AP双级配推进剂来说，用某一不同粒度AP替代双级配中粗粒度含量时，首选需要判断该替换AP粒度与被替换AP粒度大小关系，如果替换AP粒度＞被替换AP粒度时，在中低频响应函数呈增大的趋势变化，而在中高频呈降低的趋势变化；如果AP粒度＞被替换AP粒度时，响应函数变化规律相反，即在中低频呈下降的趋势变化，而在中高频呈增大的趋势变化。此规律可以同样适用于AP三级配和四级配推进剂。因此，对于AP粒度级配对响应函数的影响，需要根据AP粒度替代关系进行具体分析，并且在不同的振荡频率条件下，变化规律完全不同。