基于IMM-UPF的锂电池寿命估计

刘新天　张恒　何耀　郑昕昕　曾国建

摘   要：提出了一种基于交互式多模型（Interacting Multiple Model，IMM）和无迹粒子滤波算法（Unscented Particle Filter，UPF）的锂电池健康状态（State of Health，SOH）估计方法，针对目前SOH估计方法需求样本量大、不适用于全寿命周期结果跟踪等问题，建立了基于多项式模型、双指数模型和集成模型的IMM，通过UPF解决了重采样过程中粒子贫化的问题，根据滤波的结果对锂电池的SOH进行预测，实现了锂电池全寿命周期内的SOH精确估计. 讨论了IMM的选型依据和建模方法，给出了详细的SOH估计算法，并通过仿真和实验对不同模型进行对比. 仿真和实验结果表明，所提出的基于IMM-UPF的锂电池SOH估计结果的概率密度函数标准偏差仅为19，实现了高估计精度.

关键词：锂电池;健康状态;经验模型;交互式多模型;无迹粒子滤波

中图分类号：TM912                               文献标志码：A

Abstract：Aiming at the problem that the current SOH estimation method requires a large sample size and is not suitable for tracking the results of the whole life cycle，this paper proposed a lithium battery health state estimation method based on Interacting Multiple Model（IMM） and Unscented Particle Filter（UPF） algorithm. Through the establishment of IMM model based on polynomial model，double exponential model and integrated model and the use of UPF filter to solve the problem of particle dilution in resampling process，the SOH of lithium battery was predicted according to the results of filter，and the accurate estimation of SOH in the whole life cycle of lithium battery was realized. In this paper，the selection basis and modeling method of IMM were discussed，the detailed SOH estimation algorithm was given，and the different models were compared by simulation and experiment. The simulation and experiment results show that the standard deviation of probability density function of the proposed IMM-UPF based SOH estimation result of lithium battery is only 19，which achieves high estimation accuracy.

Key words：lithium battery;state of health;empirical models;interacting multiple model;unscented particle filter

鋰电池因其具有高能量比、高效率、循环寿命长等显著特点，而成为未来电子市场的首选电源[1]. 与铅酸电池和镍氢电池相比，锂电池因为可高温存储、快速充电、输出功率大且没有记忆效应等优点在车辆和固定式动力系统中得到广泛应用[2].

作为电池管理系统（Battery Management System，BMS）的核心环节之一[3-4]，健康状态（State of Health，SOH）因为能够提供准确的数据，达到延长电池使用寿命的目的，因此在电池使用方面发挥着至关重要的作用. 然而，由于电池使用期间伴随着复杂的物理和化学反应，锂电池的性能在使用一定时间后以非线性的形式恶化[5]，这就给锂电池状态的预测带来了很大的不确定性[6].

目前，锂电池状态估计的方法可以分为3大类：基于物理原理建模法[7-11]、基于数据建模法[12-15]和两者相结合的方法[16]. 基于物理原理建模法通常通过建立物理模型和经验模型来描述锂电池的物理和失效机制，然后建立相应的数学函数. Tsang等人[17]对锂电池等效直流电阻的测量开发了锂电池SOH的估算方案. Ning等人[18]根据负极内的不可逆电化学反应和正电极的氧化反应，建立了SOH估算模型. Singh等人[19]开发了一种基于模糊逻辑的锂离子电池SOH估算方法，其中电化学阻抗谱（Electrochemical Impedance Spectroscopy，EIS）测量值作为模糊逻辑模型的输入量.

基于物理原理建模的方法在有些时候可以准确地预测容量衰减. 然而，对于复杂的动态系统，特别是具有不确定噪声的系统，通常很难建立精确的分析模型，更不用说这些模型通常局限于特定锂电池类型. 另一方面，基于数据建模的方法可以捕捉数据中的内在关系并学习数据中所呈现的变化趋势，而不需要材料特性、结构、失效机制等方面的具体知识，避免了开发过于复杂的物理模型，使得它比基于物理原理建模的方法更易于实际操作.

近年來，由于对物理失效机制的依赖性较小，基于数据建模的方法得到了广泛的研究. 例如，Guo等人[20]研究了一种新的贝叶斯方法，可以在不同的条件下对锂电池的剩余寿命（Remaining Useful Life，RUL）进行准确预测. Miao等人[21]提出了一种改进无迹粒子滤波（Unscented Particle Filter，UPF）算法，该算法能够准确地预测锂电池实际剩余寿命（RUL），预测误差小于5%.  He等人[22]使用d-s证据理论和贝叶斯蒙特卡洛方法对经验模型进行剩余寿命（RUL）预测.

基于数据建模的方法因具有简单易操作的特点，应用较为广泛. 考查锂电池的整个寿命周期，容量衰减趋势可分为两个阶段：第一阶段为缓慢衰减阶段，SOH衰减速度缓慢且时间较长;随后是快速衰减阶段，SOH的值迅速下降且用时较短. 因此，常用的单一经验模型可能在不同阶段取得很好的预测效果，但是无法很好地描述锂电池的整个寿命周期的变化趋势. 同时，经验模型的初始参数确定需要大量的实验数据，意味着在样本数量不多的情况下，对锂电池的剩余寿命（RUL）预测将产生较大误差. 为了解决这些问题，本文提出了一种新的融合模型交互式多模型（Interacting Multiple Model，IMM），用于对不同的衰减模型融合计算. 与经典的IMM使用卡尔曼滤波（Kalman Filter，KF）不同，考虑锂电池衰减呈现非高斯和非线性的趋势使用卡尔曼滤波存在较大的误差，本文拟使用无迹粒子滤波（UPF）对各模型进行滤波，一方面解决了粒子滤波（Particle Filter，PF）在重采样过程中粒子贫化的问题，另一方面又比卡尔曼滤波得到了更准确的预测结果[23]. 最后通过仿真结果和实验数据对比的方法对本文提出的IMM-UPF方法进行了验证，结果表明该方法可以实现对剩余寿命（RUL）较准确的预测.

1   容量衰减模型

1.1   锂电池容量测量

本文使用的实验数据来源于马里兰大学高等生命周期工程中心（CALCE）[24].

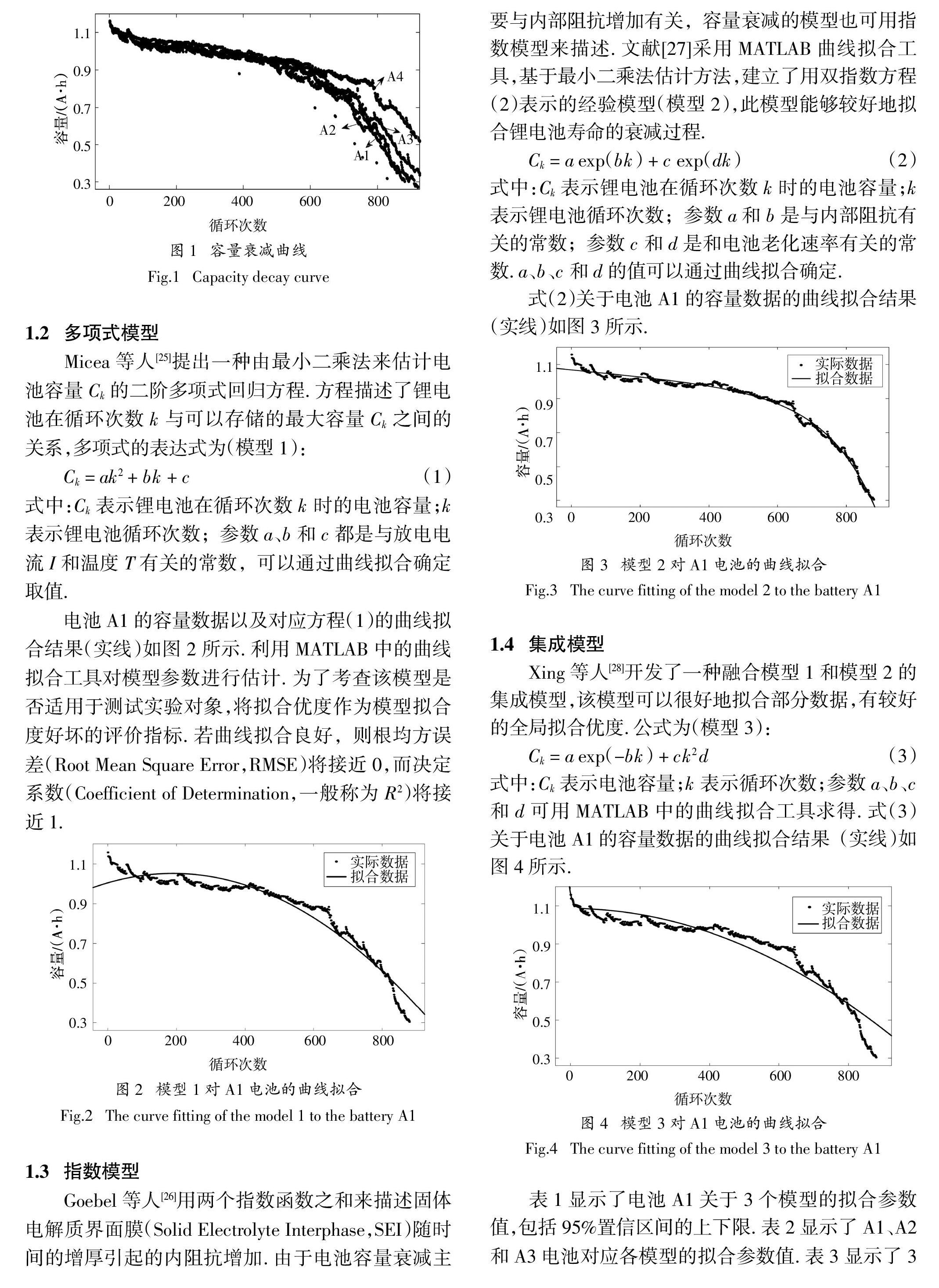
实验所用的锂电池额定容量为1 100 mA·h. 4个电池都遵循相同的标准恒定电流/恒定电压协议：首先以恒定1 C电流充电，直到电压达到4.2 V，然后以4.2 V恒压充电，直到充电电流降至0.05 A以下后，结束充电. 在室温下（25 ℃）进行充放电实验，记录每一次完全充放电过程后的放电容量. 容量衰减曲线如图1所示，电池的失效阈值（Failure Threshold，FT）设为880 mA·h（即SOH=80%时对应的电池容量）.

在本文中，有4组容量数据A1、A2、A3和A4，如图1所示，图中每一条线代表电池最大可用容量和循环次数之间的关系. 与A1、A2和A3电池相比，A4与其他电池存在较大的差异性，为了验证本文方法的准确性，电池A1、A2、A3的数据将用于确定各单一模型参数的初始值，A4电池的数据将被用来对本文方法预测准确性的验证.

3.2   仿真与实验结果分析

在仿真中，使用前300组数据作为训练数据，失效阈值为SOH=0.8，即容量Ck = 0.88 A·h，电池实际寿命为665. 即当 =0.88 A·h时，对应的A4电池循环次数为665次.

为了验证本文提出算法的有效性，使用绝对误差和剩余寿命（RUL）概率密度函数（PDF）的标准偏差来衡量仿真结果的准确性和稳定性[30].

图6、图7和图8显示了仅使用UPF算法对A4电池的模型1、模型2和模型3的预测曲线. 模型1和模型3的预测结果分别为424和530，即预测结果的绝对误差分别为241和135，RUL的标准偏差分别为48和42. 模型2在SOH = 0.8时的预测结果为706，绝对误差为41，RUL的标准偏差为37.

图9显示了用IMM-UPF算法得到的电池A4的寿命预测曲线. 当SOH=0.8时算法的仿真结果为675，对应的绝对误差为10，RUL的标准偏差为19.

4   结   论

1）通过对电池数据的采集和曲线拟合工具的使用，发现多项式模型、双指数模型和集成模型可以较好地拟合锂电池容量衰减过程. 在对各模型初始参数值的确定中，发现在给定相同的样本数量时，多项式模型和集成模型预测结果误差相对较大，且稳定性较差，虽然双指数模型在剩余寿命（RUL）的预测绝对误差较小，但概率分布（PDF）的标准差较大，即预测的稳定性也较差. 单一模型较难满足锂电池剩余寿命准确估计的要求.

2）交互式多模型的使用，使得预测结果不仅实现了对各模型初始参数的精确性依赖度下降，提高了实际使用时的效率和降低了成本，而且减小了预测误差，且RUL-PDF分布更窄，即预测结果更加稳定，是一种实际使用中可行的锂电池寿命预测方法. 本文最后通过仿真与实验结果相比较的方法，比较了单模型使用UPF算法和多模型使用IMM-UPF算法对SOH 进行估计的误差，结果表明，IMM-UPF算法减少了预测的误差，具有较好的精度，即稳定性更好.

参考文献

[1]    SCROSATI B，GARCHE J. Lithium batteries：Status，prospects and future[J]. Journal of Power Sources，2010，195（9）：2419—2430.

[2]   TAKAMI N，INAGAKI H，TATEBAYASHI Y，et al. High-power and long-life lithium-ion batteries using lithium titanium oxide anode for automotive and stationary power applications[J]. Journal of Power Sources，2013，244：469—475.

[3]    刘新天，李贺，何耀，等.基于IUPF算法与可变参数电池模的SOC估计方法[J]. 东南大学学报（自然科學版），2018，48（1）：54—62.

LIU X T，LI H，HE Y，et al. SOC estimation method based on IUPF algorithm and variable parameter battery model [J]. Journal of Southeast University （Natural Science Edition），2018，48（1）：54—62. （In Chinese）

[4]    刘新天，孙张驰，何耀，等. 基于环境变量建模的锂电池SOC估计方法[J]. 东南大学学报（自然科学版），2017，47（2）：306—312.

LIU X T，SUN Z C，HE Y，et al. SOC estimation method based on lithium-ion cell model considering environmental factors[J]. Journal of Southeast University （Natural Science Edition），2017，47（2）：306—312. （In Chinese）

[5]    陈燕虹，吴伟静，刘宏伟，等. 电动汽车锂离子动力电池分选方法研究[J]. 湖南大学学报（自然科学版），2016，43（10）：23—31.

CHEN Y H，WU W J，LIU H W，et al. Study on sorting technology for lithium-ion power battery of electric vehicle [J]. Journal of Hunan University （Natural Sciences），2016，43（10）：23—31. （In Chinese）

[6]    ZHANG J L，LEE J. A review on prognostics and health monitoring of Li-ion battery[J]. Journal of Power Sources，2011，196（15）：6007—6014.

[7]    戴海峰，魏学哲，孙泽昌.基于等效电路的内阻自适应锂离子电池模型[J]. 同济大学学报（自然科学版），2010，38（1）：98—102.

DAI H F，WEI X Z，SUN Z C. An inner resistance adaptive model based on equivalent circuit of lithium-ion batteries[J]. Journal of Tongji University （Natural Science），2010，38（1）：98—102. （In Chinese）

[8]    刘璇，王立欣，吕超，等. 锂离子电池建模与参数识别[J]. 电源学报，2018，16（1）：145—150.

LIU X，WANG L X，L? C，et al. Modeling and parameter identification for lithium-ion battery[J]. Journal of Power Supply，2018，16（1）：145—150. （In Chinese）

[9]    YANG F F，WANG D，XING Y J，et al. Prognostics of Li （NiMnCo） O2-based lithium-ion batteries using a novel battery degradation model[J]. Microelectronics Reliability，2017，70：70—78.

[10]  程泽，吕继考，刘继光，等. 等效滞回模型在锂离子电池SOC估计中的应用[J]. 湖南大学学报（自然科学版），2015，42（4）：63—70.

CHENG Z，L? J K，LIU J G，et al. Application of equivalent hysteresis model in estimation of state of charge of lithium-ion battery[J]. Journal of Hunan University（Naturnal Sciences），2015，42（4）：63—70. （In Chinese）

[11]  吕超，刘珊珊，沈杰，等. 锂离子电池等效电路模型的比较研究[J]. 电源技术应用，2014，17（9）：8—11.

L? C，LIU S S，SHEN J，et al. Comparison and research in equal circuit models of lithium-ion battery[J]. Journal of Power Technology Application，2014，17（9）：8—11. （In Chinese）

[12] SAHA B，GOEBEL K，CHRISTOPHERSEN J. Comparison of prognostic algorithms for estimating remaining useful life of batteries[J]. Transactions of the Institute of Measurement and Control，2009，31（3/4）：293—308.

[13]  PILLER S，PERRIN M，JOSSEN A. Methods for state-of-charge determination and their applications[J]. Journal of Power Sources，2001，96（1）：113—120.

[14] RAND D A J，MOSELEY P T，GARCHE J，et al. Valve-regulated lead-acid batteries [J]. Elsevier，2001，95（1）：2—12.

[15]  DAI J，DAS D，OHADI M，et al. Reliability risk mitigation of free air cooling through prognostics and health management [J]. Applied Energy，2013，111：104—112.

[16]  DALAL M，MA J，HE D. Lithium-ion battery life prognostic health management system using particle filtering framework[J]. Journal of Risk and Reliability，2011，225（1）：81—90.

[17]  TSANG K M，CHAN W L. State of health detection for Lithium ion batteries in photovoltaic system [J]. Energy Conversion and Management，2013，65：7—12.

[18]  NING G，HARAN B，POPOV B N. Capacity fade study of lithium-ion batteries cycled at high discharge rates[J]. Journal of Power Sources，2003，117（1/2）：160—169.

[19]  SINGH P，VINJAMURI R，WANG X Q，et al. Fuzzy logic modeling of EIS measurements on lithium-ion batteries [J]. Electrochim Acta，2006，51（8/9）：1673—1679.

[20]  GUO J，LI Z J，PECHT M. A Bayesian approach for Li-ion battery capacity fade modeling and cycles to failure prognostics[J]. Journal of Power Sources，2015，281：173—184.

[21]  MIAO Q，XIE L，CUI H J，et al. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique[J]. Microelectronics Reliability，2013，53（6）：805—810.

[22]  HE W，WILLIARD N，OSTERMAN M，et al. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources，2011，196（23）：10314—10321.

[23]  曲彥文，张二华，杨静宇. 改进的无迹粒子滤波算法[J]. 控制理论与应用，2010，27（9）：1152—1158.

QU Y W，ZHANG E H，YANG J Y. Improved unscented particle filter [J]. Control Theory & Applications，2010，27（9）：1152—1158. （In Chinese）

[24]  LIU J，SAXENA A，GOEBEL K，et al. An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries [C]//Annual Conference of Prognostics and Health Management Society 2010. Ottawa：Department of Mechanical and Aerospace Engineering，Carleton University，2010：1—9.

[25]  MICEA M V，UNGUREAN L，C?RSTOIU G N，et al. Online state-of-health assessment for battery management systems [J]. IEEE Transactions on Instrumentation and Measurement，2011，60（6）：1997—2006.

[26] GOEBEL K，SAHA B，SAXENA A，et al. Prognostics in battery health management [J]. IEEE Instrumentation and Measurement Magazine，2008，11（4） ：33—40.

[27] ARULAMPALAM M S，MASKELL S，GORDON N，et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing，2002，50（2）：174—188.

[28]  XING Y J，MA E W M，TSUI K L，et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries[J]. Microelectronics Reliability，2013，53（6）：811—820.

[29]  邸忆，顾晓辉，龙飞，等. 一种基于改进UPF的运动声阵列交互多模型目标跟踪方法 [J]. 控制与决策，2018，33（2）：249—255.

DI Y，GU X H，LONG F，et al. An improved UPF-based interacting multiple model target tracking method for dynamic acoustic array [J]. Control and Decision，2018，33（2）：249—255. （In Chinese）

[30]  CRIPPS E，PECHT M. A Bayesian nonlinear random effects model for identification of defective batteries from lot samples[J]. Journal of Power Sources，2017，342：342—350.