基于海图和ASTER GDEM数据融合的水陆一体连续地形构建
2020-04-17王炎田雨
王炎,田雨
(中交上海航道勘察设计研究院有限公司,上海 200120)
河口海岸地区经济发达,人类活动频繁,大型工程密集,地形演变事关堤岸、航运及港口安全,是地理学和工程学研究的主要方向[1-4]。由于该地区环境复杂,常规测绘方法效率低、成本高,通常伴随大量多余观测,利用当前的测量设备需耗费大量时间才能完全覆盖河口地区[5-7]。ASTER GDEM(The Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Mode)数据的发布使得公众可以免费获取全球范围内分辨率30 m的地形数据[8-9],已广泛应用于工程开发、地质与灾害评估等领域[10],但受采集方式的限制,ASTER GDEM数据缺乏对水下地形的描述。若能充分利用该地区的海图数据与ASTER GDEM数据进行融合,将是快速获取水陆一体连续地形的有效途径。
ASTER GDEM数据与海图数据的融合主要存在两个问题:一为空间参考系不统一[11];二为原始数据精度不一致[12]。这会导致融合边界处的高程值与周围高程值存在明显差异。一些学者对如何处理该高程差异开展了相关研究。如许家琨等[13]总结了我国海岸带地形测量涉及到的垂直基准面并探讨了各基面间的转换关系;Kuuskivi等[14]对融合边界处不连续数据进行平滑处理,但会改变已知高程,给融合结果带来不必要的精度损失;Alca^ntara等[15]提取出SRTM与历史地形图的等高线信息并合并,通过内插重新生成高程模型,但融合结果空间分辨率较低;凌峰等[12]对融合数据的高程差异空间相关性进行分析,有效减小了两种数据间的相对误差,但缺乏绝对精度分析;受制于多源数据获取机理与数据特性的差异,地形数据间的无缝融合仍是国内外研究的难点[10],特别是ASTER GDEM数据精度远低于海图数据精度,有关其融合过程中的误差校正研究尚未见报道。
本文以长江口南支测区为研究地区,分析了ASTER GDEM数据与海图数据间的差异并对该地区ASTER GDEM数据与海图数据进行融合研究。针对ASTER GDEM原始数据精度较低的缺陷,利用曲面拟合法对其进行误差校正,不仅减少了融合数据间的高程差异,而且也增强了数据后期使用的可靠性。本方法可以实现区域尺度的水陆一体连续地形模型的快速构建,为河口地区的野外测量任务规划提供决策依据,从而减少多余观测,提高测量效率,降低工作成本。
1 研究方法
1.1 海图与ASTER GDEM数据差异分析
海图是地图的一种,是按照水上航行需求绘制的地图,符合GB 12319—1998《中国海图图式》,包含了岸形、岛屿、礁石、水深、航标和无线电导航台等内容[16]。海图数据重点表示水深信息和影响舰船航行的海部要素,岸线以上的地形要素主要根据地形图编绘,仅有少量地面控制点含有高程信息。
ASTER GDEM数据是美国国家航天局(NASA)与日本经济产业省(METI)根据Terra卫星所获取的150万景近红外影像,基于同轨立体摄影测量原理制作完成的,属于地球观测系统(EOS)计划的一部分[17],覆盖范围为 83°N—83°S,是迄今为止可为公众免费下载的最完整、最可靠的全球数字高程数据[8]。图1展示了长江口地区ASTER GDEM数据图像,从图上可以看出,因为光学传感器的采集特性,水陆交界处存在大量异常数据,因此在使用ASTER GDEM数据前,需结合当地地形特征对异常数据进行探测并剔除。

图1 长江口地区ASTER GDEM数据图像Fig.1 ASTER GDEM imagery of Yangtze estuary
表1列出了ASTER GDEM与海图数据的基本信息对照,两者在空间参考系方面存在较大差异。空间坐标系方面,海图数据采用的CGCS2000坐标系与ASTER GDEM采用的WGS-84坐标系的基本定义是一致的,参考椭球体非常接近,仅有扁率这一常数有细微差别,但在当前测量精度水平下这种微小差值可以忽略;在垂直基准方面,海图数据采用理论最低潮面作为高程基准,与ASTER GDEM数据所采用的EGM96高程基准存在系统误差,不可避免的存在陆地高程与水深数据不能有效衔接的缺陷,故需要通过水准测量,建立两种数据源垂直基准间的转换数学模型[18]。

表1 海图与ASTER GDEM数据基本信息表Table 1 Basic information of bathymetric map and ASTER GDEM data
1.2 基于曲面拟合算法的ASTER GDEM误差校正
ASTER GDEM数据在我国范围内都是通过无控制点测量所得,垂直精度约为±20 m,即使在精度最高的平原地区也达到±5 m[19-20],因此无法直接用于高精度水陆一体连续地形模型的构建,而必须对高程误差进行校正后再与海图数据进行融合。
传统的误差校正方法首先统计两种数据重叠区域的高程差值,建立回归方程,然后在误差均方根最小的情况下对融合数据进行变换[21]。该方法对参与融合的高程数据均做相同处理,实际上,由传感器构造特点,环境变化等因素产生的误差组分通常具有空间相关性[22],传统方法没有考虑到这一点,给融合结果带来不必要的精度损失。
为了提高融合结果的数据精度,一种更好的办法就是利用高精度地面控制点对ASTER GDEM数据进行误差校正。两种高程数据间的关系可以表达为:

式中:H(x,y)表示坐标(x,y)处的地面控制点高程值;A(x,y)表示坐标(x,y)处的 ASTER GDEM 数据高程值,E(x,y)表示坐标(x,y)处的 ASTER GDEM高程误差。考虑到部分误差组分具有空间相关性,本文采用二次曲面拟合方法建立高程误差E(x,y)与空间位置(x,y)之间的相关关系,进而根据该相关关系拟合出整个区域的误差曲面,实现区域内ASTER GDEM高程数据的误差校正。
二次曲面拟合法公式如下:
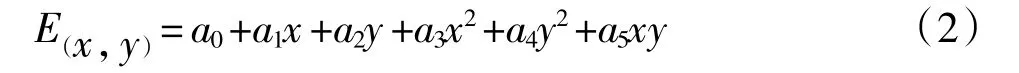
为了进一步提高求解精度,参与拟合计算的点数应多于未知参数个数,通过参数平差原理进行求解[23],误差方程如下:

式中:a0,a1,…,a5即为拟合参数,首先根据控制点位坐标(x,y)和对应高程误差 E(x,y)对其进行求解,再反过来将拟合参数和其余ASTER GDEM像元坐标代入式(3)即可求得相应位置的高程误差,从而生成误差曲面,对区域内ASTER GDEM高程数据进行校正。
1.3 方法实现
基于上述方法构建水陆一体连续地形模型的技术流程如图2所示。第一步要对多源数据进行空间基准的统一,平面基准统一至CGCS2000坐标系,垂直基准统一至1985国家高程基准(似大地水准面)。郭海荣[24]的研究表明,1985国家高程基准点与EGM96高程基准之间有35.7 cm的系统垂直偏差,且自东向西明显增大,海图数据提供有对应年份的平均海面高度,以此建立两种垂直基准间的数学转换模型。
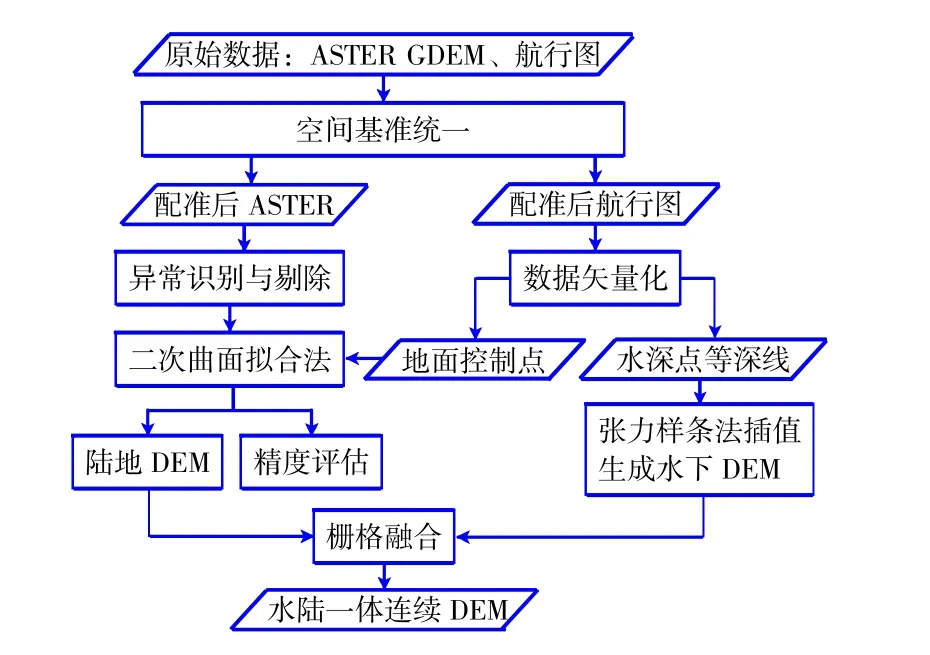
图2 基于海图和ASTER GDEM数据融合构建水陆一体连续地形模型技术流程图Fig.2 Flowchartofthemethodthatintegratingbathymetric maps and ASTER GDEM data to build continuous terrain of water-land integration
随后对ASTER GDEM数据进行水陆分离。通常而言,ASTER GDEM中水面数据为一定值,可通过设置阈值进行提取。但镜面反射等因素导致的异常数据会对分离结果造成干扰,因此还要借助准确的岸线信息。航行图中定义的岸线位置为平均大潮高潮位时水陆分界的痕迹线,在堤防工程完善的地区也可借助其他遥感影像获得岸线的位置和形态[25]。结合实地情况,融合航行图与遥感影像提供的岸线位置,以此作为分界线,对ASTER GDEM进行水陆分离。水面数据作为无效数据进行剔除。陆地数据采用二次曲面拟合法进行误差校正并进行精度评估。
海图提供了所在区域的水深信息,但多为离散点和等深线,需要进一步内插处理生成DEM格网来填补ASTER GDEM数据的水域空白。常规的插值算法产生的产品质量取决于采样点的密度,在数据稀疏区会形成假值,不适于水下地形模型的建立[26]。样条函数插值算法虽然能通过已知点建立光滑的曲面,但在地形急剧变化地带,光滑的特性反而掩盖了地形本来的不连续特征[27]。目前,张力样条插值法(Tension Spline)是构建海底地形模型的标准插值算法[28-30],通过张力因子的设置进一步控制了插值超限的现象,也是众多插值算法中精度最高的。
最后,将新生成的陆地DEM与水下DEM进行镶嵌合并处理,生成水陆一体连续地形模型。
2 实验结果与分析
下面以长江口地区南支水道为试验区域,检验上述方法的实际效果,在进行数据融合前,首先利用已有资料将海图数据配准到ASTER GDEM数据,垂直基准转换至1985国家高程基准,并将离散化的水深点、等深线按照张力样条法插值生成水下DEM。

图3 地形模型构建效果Fig.3 Effect of terrain model construction
处理结果如图3所示,图3(a)为ASTER GDEM原始数据图像,长江口地区受径流、潮流、波浪和复杂地形等因素影响,多变的动力条件[31]、复杂的泥沙输运以及大面积水体造成的镜面反射效应,都影响了光学传感器的数据质量,图中水面附近的高亮度格网为异常数据,图3(b)是本次试验的融合结果,原始数据中的大量异常数据得到有效修复,深水航道与江中浅滩清晰可辨,区域内高程值集中在46~-46 m之间,与实际情况相符。
为对本方法的效果进行定量分析,采用中误差(RMSE)为评价指标比较校正前后的精度差异,当研究区域地形起伏不大且控制点位分布均匀时,二次曲面拟合法有着较高的精度。如图4所示,本次实验收集地面控制点13个,其中10个点进行拟合计算求解参数,另外3个点用作校核计算,验证拟合精度。点位详细信息见表2。比较控制点水准高程与对应点位处ASTER像元值,原始数据中误差(RMSE)为6.282 m。经过二次曲面拟合计算后的点位信息见表3。拟合计算后的点位中误差(RMSE)为0.445 m。可以看到基于二次曲面拟合的误差校正可以有效提高原始数据高程精度。

图4 研究区域控制点点位分布Fig.4 The distribution of regional control points in study area

表2 控制点点位信息表Table 2 Detail information of control point m

表3 拟合像元值与水准高程对比Table 3 The comparison between geoid elevation and pixel value with fitting
为了进一步观察海图与ASTER GDEM数据的融合效果,分别在分流口、南支主槽选取贯穿水陆的典型剖面,如图5所示。由剖面图(图5(b)、(d)、(f))可以看出,两条剖面所处区域的原始数据均有明显的“跳点”现象,地形多处突变与实际严重不符。基于海图和ASTER GDEM数据融合构建的水陆一体连续地形模型的剖面图(图5(a)、(c)、(e))则较真实地反映了水陆地形,地形剖面变化平缓,水陆交界处无明显跳跃。结果表明,本方法有效改善地形数据融合过程中存在的高程差异问题,提高ASTER GDEM高程精度,能够快速构建水陆一体连续地形模型。

图5 典型剖面地形对比Fig.5 Typical profile topography comparison
3 结语
以含有准确高程信息的地物数据作为辅助,可在地形数据融合过程中提供一定的附加空间信息和限定条件,从而有助于获得更为准确的融合结果。本文采用高精度地面控制点作为辅助信息,以长江口测区为例,对海图数据与ASTER GDEM数据进行差异分析与融合试验。实现了区域尺度的水陆一体连续地形模型的快速构建。该地形模型可用作布置野外测量任务的决策依据,有效克服了河口地区野外测量工作中存在的测量数据冗余、测量目标不直观等缺陷。
本文的融合方法具有原始数据易获取、融合结果精度高等优点,但融合结果可能与研究区地形特点相关。本次研究区域地形平坦,数据波动较小,二次曲面拟合法能取得较好效果,在地形急剧变化的地区,该方法有待进一步验证。此外,由于地面控制点数量较少,研究区域相对较大,高程误差的空间相关关系有待进一步验证。即便如此,在其他地形数据的情况下,基于海图与ASTER GDEM数据融合的方法,可以快速构建所在区域的全面地形信息,从而为相关研究提供更精确的基础地形资料。
