电动车自适应ESP控制算法设计与仿真分析

姚树桐 崔淑华 王宪彬

摘 要：  针对某单电机后置后驱纯电动车型，进行横向稳定性控制算法的设计与仿真分析。采用模糊算法识别路面附着系数，设计以车辆横摆角速度与质心侧偏角为控制目标的自适应模糊PID附加橫摆力矩控制策略，采用四通道差动制动控制策略对制动力矩进行分配。基于CarSim与Matlab/Simulink联合仿真环境，分别在高、低附着系数路面进行不同初速度下的蛇形试验工况仿真对比分析。仿真结果表明，所提出的基于模糊PID的自适应ESP控制算法可以有效改善不同附着系数路面上该车型的横向稳定性，为该车型在实际研发过程中遇到的横向稳定性仿真优化问题提供了可行的解决思路。

关键词： 电动汽车;ESP;自适应模糊PID;差动制动

中图分类号 ：U461.6;U461.91    文献标识码 ：A    文章编号 ：1006-8023（2020）02-0103-08

The Design and Simulation of Adaptive ESP Control Algorithm for Electric Vehicle

YAO Shutong， CUI Shuhua*， WANG Xianbin

（School of Traffic and Transportation， Northeast Forestry University， Harbin 150040， China）

Abstract： The lateral stability controller algorithm design and simulation test analysis were carried out for a single motor rear-drive pure electric vehicle. Fuzzy algorithm was used to identify the road adhesion coefficient. An adaptive fuzzy PID yaw moment control strategy was designed， which took yaw velocity and sideslip angle of the mass center as control targets. Four-channel single-wheel differential braking control strategy was used to distribute braking torque. Based on the co-simulation environment of CarSim and Matlab/Simulink， the serpentine test conditions of high and low adhesion road surface were simulated and compared under different initial speeds. The simulation results showed that the proposed adaptive ESP control algorithm based on fuzzy PID could effectively improve the lateral stability of the vehicle on roads with different adhesion coefficients. It provides a feasible solution to the problem of simulation and optimization of actual research and development of this vehicle.

Keywords： Electric car; ESP; adaptive fuzzy PID; differential braking

收稿日期： 2019-11-08

基金项目： 黑龙江省自然科学基金项目（E2015052）

第一作者简介： 姚树桐，硕士研究生。研究方向：汽车技术状态监测及性能仿真。E-mail：18746682529@163.com

*通信作者： 崔淑华，硕士，教授。研究方向：汽车节能减排技术。E-mail：csh1218@163.com

引文格式： 姚树桐，崔淑华，王宪彬. 电动车自适应ESP控制算法设计与仿真分析[J].森林工程，2020，36（2）：103-110.

YAO S T，CUI S H，WANG X B. The design and simulation of adaptive ESP control algorithm for electric vehicle[J].Forest Engineering，2020，36（2）：103-110.

0 引言

ESP（Electronic Stability Program）是指汽车“电子稳定控制程序”。对于ESP系统，国内外学者进行了控制器的开发和控制策略的研究。韩顺等[1]设计了基于自适应模糊神经网络ESP控制策略，并通过仿真验证了策略有效性。方春杰 [2]搭建了ESP控制系统的LQG控制模型，并通过双移线仿真试验验证了设计的有效性。吴刚院等[3]提出了一种随外界条件变化的变阈值车辆横向稳定性控制方法，并通过联合仿真验证了设计的有效性。肖佩等[4]建立了基于递推二乘法的路面附着系数在线辨识模型，通过仿真，验证了控制策略的优越性。Mauro[5]利用硬件在环试验对ESP液压调节系统进行了动态性能测试，得出不同部件对控制性能的影响。Paul等[6]从能量回收以及路面附着系数辨识方面，对差动制动策略进行了改进及优化。Her等[7]提出了一种基于主动侧倾力矩控制的底盘集成控制策略。Zhu等[8]提出了基于神经网络和侧翻时间的侧翻预警算法，提高了车辆侧翻预警精度和横向稳定性。Lúa等[9]设计车辆控制器进行参数识别并跟踪参考模型轨迹，利用双转向试验验证了算法的有效性。

以上学者从不同角度进行了车辆行驶稳定性的控制策略研究，但对于电动车在不同路面附着条件下的自适应控制研究较少。本文针对某单电机后置后驱纯电动车型，进行了车辆行驶横向稳定性自适应控制研究，提出了路面附着系数的模糊识别算法和自适应模糊PID附加横摆力矩控制策略;通过CarSim与MATLAB/Simulink联合仿真，对蛇形试验工况下不同附着系数路面上控制算法有效性进行了验证。为该车型在实际研发过程中遇到的横向稳定性仿真优化问题提供了可行的解决思路。

1 CarSim车辆模型建立

1.1 整车建模

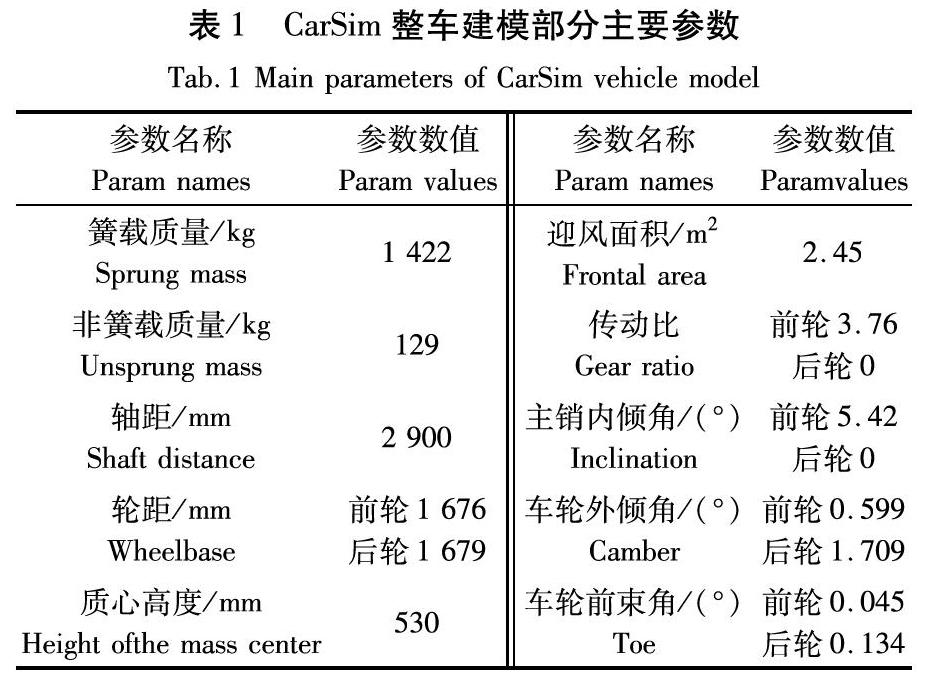
根据目标车型数据，在CarSim中建立D-Class Sedan车辆模型，由于 CarSim中D-Class Sedan车辆模型的默认动力源为内燃机，因而需要利用外部的电机模型替换内燃机模型。车辆主要参数见表1。

1.2 电机建模

本文根据电机动力学特性搭建基于Simulink的驱动电机动力学简化模型。该电机模型的输入为纵向车速、踏板行程比例系数;输出为电机输出转矩，计算公式为：

T0= 9 550Pe n 。T*max=min T0，Tmax 。Treq=AmT*maxn= 60uK 3.6·2πr 。umax= 3.6·2πrn 60K 。T=Treq。     （1）

式中：Pe为额定功率，kW;n为电机转速，r/min;T0为电机额定功率下的转矩，N·m;Tmax为电机最大转矩设定值，N·m;T*max为电机最大输出转矩，N·m;Am为加速踏板行程比例系数;u为车速，km/h;umax为最高车速，km/h;r为车轮滚动半径，m;K为传动系传动比;Treq为需求转矩，N·m;T为电机输出转矩，N·m。

根据目标车型实际匹配情况，其中电机额定功率Pe为175 kW，最大转矩设定值Tmax为320 N·m，最高车速umax为195 km/h。根据公式（1）及电机参数搭建驱动电机动力学模型，如图1所示。

电机的外特性仿真曲线如图2所示。

2 ESP控制算法设计

2.1 控制算法结构

本文提出的控制算法包括上、中、下3层控制器：上层为识别层，首先通过轮胎纵向力Fx和轮胎垂向力Fz计算得出当前的利用附着系数φ，并以利用附着系数φ和车轮滑移率α为输入，采用模糊算法识别出当前的路面附着系数μ。中层为决策层，以理想横摆角速度ωd*与理想质心侧偏角βd*为控制目标，采用自适应模糊PID控制策略得出使得车  辆稳定所需的附加横摆力矩ΔMz。下层为分配层，以前轮转角δ和横摆角速度偏差值Δω的耦合关系作为判断依据，采用四通道差动制动控制策略对制动力矩进行分配。ESP控制算法结构如图3所示。

2.2 参考模型

参考模型采用考虑汽车的侧向运动、横摆运动的线性二自由度车辆模型，其动力学方程为[6，10]：

（k1+k2）βd+（ak1-bk2）ωd/u-k1δ=m（v · +uωd）（ak1-bk2）βd+（a2k1+b2k2）ωd/u-ak1δ=Izωd ·   。   （2）

式中：m为整车质量，kg;βd为车辆理论质心侧偏角，rad;ωd为车辆理论横摆角速度，rad/s;a， b为车辆质心与前后轴之间的距离，m;Iz为汽车绕z轴的转动惯量，kg·m2;k1，k2为前后轮轮胎侧偏刚度，N/rad;δ为前轮转角，rad。

经公式（2）变换得到汽车横摆角速度ωd和质心侧偏角βd分别为：

ωd= u/L 1+Ku2 βd=ωdu（ b u2 + ma k2L ）   。 （3）

保持车辆稳定行驶的最大横摆角速度和质心侧偏角与附着系数和行驶速度相关，所以将最大横摆角速度ωdmax≤μg/u 代入公式（3）中得到最大質心侧偏角为：

βdmax=μg（ b u2 + ma k2L ） 。    （4）

式中：g为重力加速度，取9.8 m/s2;μ为路面附着系数;L为前后轴之间的距离，m。

由线性二自由度整车参考模型得到的理想横摆角速度和理想质心侧偏角整理为：

ωd*=min{| u/L 1+Ku2 |，| μg u |}·sgn（ω′d）βd*=min{|ωdu（ b u2 + ma k2L ）|，|μg（ b u2 + ma k2L ）|}·sgn（β′d） 。  （5）

根据公式（5）搭建线性二自由度车辆参考模型。

2.3 上层控制器

将CarSim整车模型和电机模型联立进行联合仿真，按照μ1=0.15、μ2=0.35、μ3=0.6、μ4=0.85、μ5=1获取5组轮胎滑移率α与利用附着系数φ的对应关系数据，其中φ=|Fx/Fz|，如图4所示。

由图4得，当轮胎滑移率α不变时，路面附着系数μ随着利用附着系数φ的增大而增大。根据不同路面附着系数μ下的利用附着系数φ与轮胎滑移率α的关系来进行模糊控制器的参数和模糊控制规则的设置，模糊控制器类型选用Sugeno型。设轮胎滑移率α的基本论域为[0，1]，利用附着系数φ的基本论域为[0，1]，量化因子均为1。模糊控制器的输入、输出曲面关系如图5所示。

综上建立识别模型如图6所示。

将路面附着系数μ识别模型与CarSim整车参数化模型进行联合仿真以验证模型的有效性，验证结果如图7所示。

由图7可以看出，路面附着系数μ识别呈现较好效果，由于极低滑移率情况下的利用附着系数φ的区分度很小（图4），因此，在极低滑移率情况下识别偏差较大，但此偏差不影响ESP的控制效果。

2.4 中层控制器

中层控制器采用横摆角速度ω与质心侧偏角β联合模糊PID控制策略，并根据当前的实际质心侧偏角βr和由上层控制器识别出的路面附着系数μ的大小，利用模糊控制理论得出β控制的分配系数ε。

2.4.1 ESP启动条件

横摆角速度ωr和质心侧偏角βr是表征车辆行驶状态的两个重要参数。在质心侧偏角βr很小的情况下，横摆角速度偏差Δω就足以表征车辆的稳定性状态，其参考取值范围如公式（6）所示[11]。

|Δω|=|ωr-ω*d|≤|cω*d|。   （6）

式中：c为常数，其值可以根据具体控制精度选取，一般取值c=0.165。

随着质心侧偏角βr的增加，此时仅仅依靠横摆角速度偏差Δω难以精确表征车辆稳定性状态，故失稳状态的判定还必须考虑车身质心侧偏角βr才能达到较好的效果。刘伟[12]利用质心侧偏角和质心侧偏角速度构造相平面对车辆稳定性状态进行分析，得出稳定区域的描述为：

|B1βr · +βr|≤μ·B2 。  （7）

式中：μ为路面附着系数;B1、B2为稳定常数，其值根据具体车型确定，经分析得出适合该整车模型的B1=0.58，B2=0.27。当公式（6）与公式（7）同时成立时候，则认为车辆没有失去稳定性，稳定性控制系统ESP无需干预，若公式（6）与公式（7）中有任意一个不等式关系不成立时，则判断为车辆失去稳定性，稳定性控制系统ESP需要进行干预以维持车辆稳定性。

2.4.2 模糊PID控制器设计

PID控制部分采用增量式PI控制，ω模糊控制器的输入为ω的实际值与名义值的偏差eω以及该偏差的微分ecω，β模糊控制器的输入为β的实际值与名义值的偏差eβ以及该偏差的微分ecβ，输出均为各自PI控制的比例參数及积分参数[kp，ki]的调整值[Δkp，Δki]。

设[eω，ecω，eβ，ecβ，Δkpω，Δkiω，Δkpβ，Δkiβ]的论域均为[-1，1]。[eω，ecω]的比例因子分别为[0.9，0.01]，[Δkpω，Δkiω]的量化因子分别为[3000，0.3]，[eβ，ecβ]的比例因子分别为[1.8，0.025]，[Δkpβ，Δkiβ ]的量化因子分别为[3 000，0.5]。隶属度函数均采用三角型和梯形，模糊控制器采用Mamdani型。

将[eω，ecω，eβ，ecβ]的模糊集均划分为5个等级[NB，NS，ZE，PS，PB]，依次为负大、负小、零区、正小、正大。设Δkpω的模糊规则的输出结果为P1，Δkiω的模糊规则的输出结果为P2，Δkpβ的模糊规则的输出结果为P3，Δkiβ的模糊规则的输出结果为P4，则模糊规则输出结果的格式为P1，P2/P3，P4，

P1，P2，P3，P4均由[Δkpω，Δkiω，Δkpβ，Δkiβ]的模糊集[NB，NM，NS，ZE，PS，PM，PB]的子集表示，NM为负中，PM为正中。模糊控制规则见表2。

综上，附加横摆力矩的计算为：

ΔMz=（1-ε）ΔMω+εΔMβ 。    （8）

式中：ΔMω为ω控制器输出的附加横摆力矩;ΔMβ为β控制器输出的附加横摆力矩;ΔMz为控制器输出的总附加横摆力矩，其中ε为分配系数。

2.4.3 系数ε的自适应协调分配规则设计

典型的系数ε分配规则为[7]：

ε=a1β   0≤β≤a3/（a2-a1）ε=a2β-a3 a3/（a2-a1）≤β≤5ε=1        β≥5  。 （9）

上述分配规则中a1、a2、a3的确定需要经过大量试验获得，且确定后灵活性较差，无法根据不同路面附着系数进行灵活调整。以下将依据该分配规则所设计的控制策略称为A控制策略。

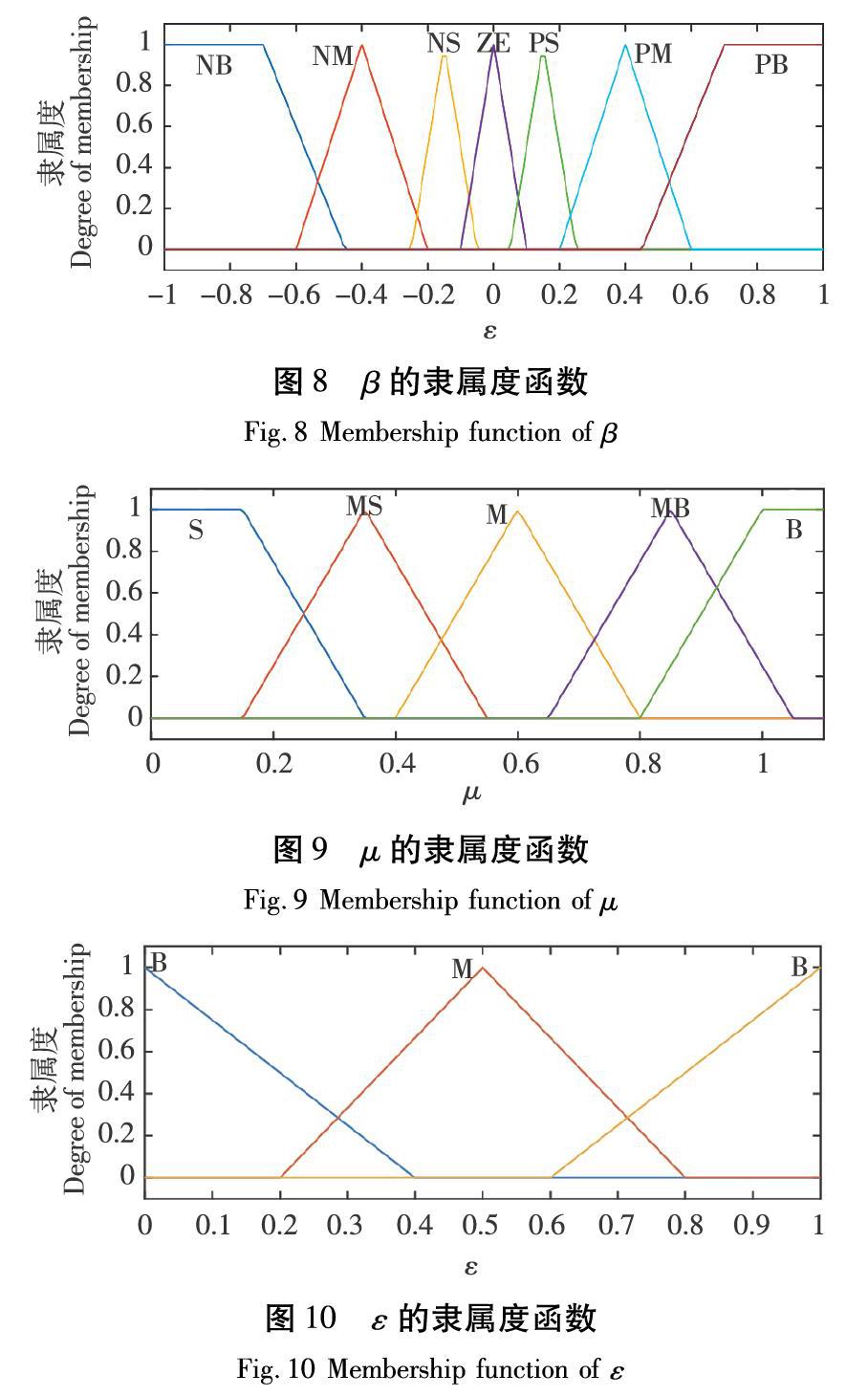
基于模糊控制理论的自适应协调分配控制器采取车辆实际质心侧偏角βr和路面附着系数μ作为输入。设βr的论域为[-1，1]，μ的论域为[0，1.1]，ε的论域为[0，1]，[β，μ]的比例因子分别为[1.8， 1];ε的量化因子为1。隶属度函数均采用三角形和梯形。β的模糊集为[NB，NM，NS，ZE，PS，PM，PB];μ的模糊集为[S，MS，M，MB，B];ε的模糊集为[B，M，S]。

输入与输出的隶属度函数如图8—图10所示。

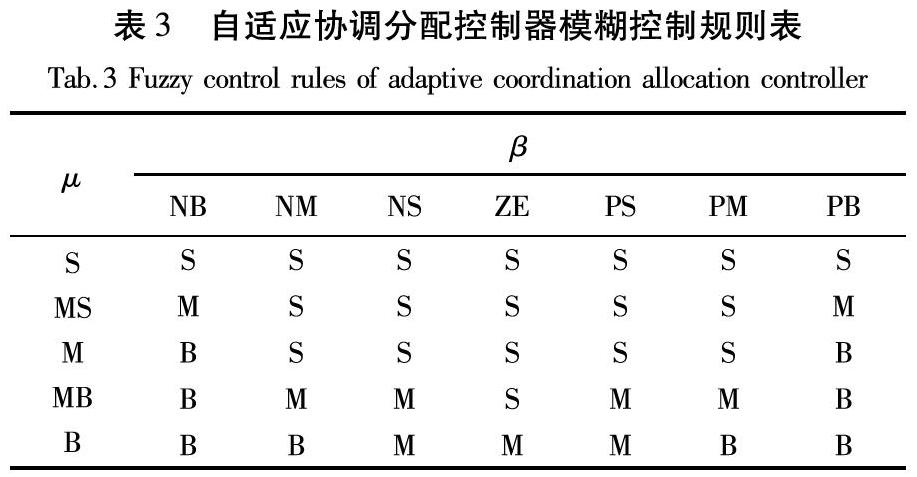
其模糊控制规则见表3。

综上建立基于B控制的中层控制器Simulink模型如图11所示。依据该模糊系数分配规则所设计的控制策略以下称为B控制策略。

2.5 下层控制器

2.5.1 四通道单轮差动制动逻辑判断

车辆附加横摆力矩ΔMz的方向取决于横摆角速度偏差Δω，所以通过判断实际横摆角速度ωr、理论横摆角速度ωd、横摆角速度偏差Δω的正 负确定制动的车轮[13-15]。假设，横摆角速度逆时针方向为正，

顺时针为负，前轮左转为正，右转为负，偏差Δω=ωr-ω*d，前轮转角δ，则差动制动逻辑见表4。

2.5.2 制动力矩分配

当车辆出现不稳定状态时，可通过控制前轮、后轮制动力矩达到恢复车辆稳定性的目的。图12为整车力学特性图[16]。

假设单独控制左侧车轮，则由图12可知[17]：

ΔMz≈Fxlf·lf/2+Fxlr·lr/2 。  （10）

式中：lf、lr分别为前后轴长度，m;Fxlf、Fxlr分别为左前轮和左后轮的地面制动力，N。

考虑到前轮转角δ比较小，且车辆的前后轮距差别也很小，故公式（10）可写为：

4ΔMz/（lf+lr）≈Fxl1+Fxl2 。  （11）

为防止车轮抱死拖滑，设定制动力上限Fxmax=μFzi。则按公式（12）进行制动力动态分配为：

Fxlf= Fzlf Fzlf+Fzlr · 4ΔMz lf+lr Fxlr= Fzlr Fzlf+Fzlr · 4ΔMz lf+lr Fxli≤Fxlmax=μFzli    。 （12）

则左侧车轮需要制动器提供的制动力矩为：

Txlf= Fzlf Fzlf+Fzlr · 4ΔMz lf+lr ·rTxlr= Fzlr Fzlf+Fzlr · 4ΔMz lf+lr ·rTxlf≤Fxlmax·r=μFzlf·rTxlr≤Fxlmax·r=μFzlr·r   。  （13）

同理可以求出汽车右侧前后车轮的制动力矩为：

Txrf= Fzrf Fzrf+Fzrr · 4ΔMz lf+Tr ·rTxlr= Fzrr Fzrf+Fzrr · 4ΔMz lf+lr ·rTxrf≤Fxrmax·r=μFzrf·rTxrr≤Fxlmax·r=μFzrr·r  。  （14）

式中：r为轮胎的滚动半径，m;Fzlf、Fzlr、Fzrf、Fzrr分别为左前轮、左后轮、右前轮、右后轮的受地面的垂直载荷，N;Txlf、Txlr、Txrf、Txrr分别为左前轮、左后轮、右前轮、右后轮的制动力矩，N·m;式中下角标i表示下角标r或f。

3 CarSim-Simulink联合仿真结果

蛇形试验工况是汽车操纵稳定性闭环控制研究中最典型的测试工况之一，该试验可以有效检验车辆的操纵稳定性。仿真工况的设定依据标准[18-19]来选取。

针对中层控制器中采取的A、B两种控制策略进行高附着路面蛇形试验（初始车速75 km/h，路面附着系数0.85）和低附着路面蛇形试验的仿真试验（初始车速55 km/h，路面附着系数0.35）。试验结果如图13—图16所示。

从图13和图14可以看出，在高附着路面条件下，无控制的车辆在10 s左右发生明显失稳，车辆在A、B两种控制策略的调节下行驶均可以保持车身稳定;但从图15和图16可以看出，在低附着路面条件下，无控制的车辆在13 s左右发生明显失稳，A控制策略所控制的车辆在17 s左右经过最后一个桩位 时发生失稳，而车辆在B控制策略的调节下行驶依旧可以保持车身稳定， 在车辆横摆角速度贴近

期望曲线的同时，质心侧偏角也一直处于较小的状态。高、低附着系数路面的蛇形工况仿真试验结果表明，B控制策略具有相对较好的自适应能力。

4 结束语

本文提出了以橫摆角速度偏差Δω和质心侧偏角偏差Δβ作为自变量，4个车轮的差动制动力矩Txlf、Txlr、Txrf、Txrr作为因变量的模糊PID自适应ESP控制算法，并且该算法在能够识别路面附着系数μ的同时，能够根据实时变化的路面附着系数μ和车辆的质心侧偏角βr实时改变控制参数ε值。CarSim和 MATLAB/Simulink联合仿真结果表明，所提出的基于模糊PID的自适应ESP控制算法在高、低附着系数的路面均能保持车辆的稳定状态。

【参 考 文 献】

[1]  韩顺，高翔.基于ESP的车辆稳定性控制策略研究[D].镇江：江苏大学，2016.

HAN S， GAO X. Study on the control strategy of vehicle stability based on ESP[D]. Zhenjiang： Jiangsu University， 2016.

[2]  方春杰.基于ESP的纯电动汽车稳定性控制及仿真[J].汽车工程师，2017，44（6）：39-43.

FANG C J. Stability control and simulation for battery electric vehicle based on ESP[J]. Automotive Engineer， 2017， 44（6）：39-43.

[3]  吴刚院，刘丹，陈娟娟.乘用车横向稳定性控制联合仿真[J].汽车技术，2018，39（3）：30-35.

WU G Y， LIU D， CHEN J J. Joint simulation of lateral stability control for passenger car[J]. Automotive Technology， 2018， 39（3）： 30-35.

[4]   肖佩，龙祥，胡剑.考虑路面附着系数的车辆差动制动控制策略[J].重庆交通大学学报（自然科学版），2018，31（11）：133-138.

XIAO P， LONG X， HU J. Vehicle differential braking control strategy considering road adhesion coefficient[J]. Journal of Chongqing Jiaotong University （Natural Science Edition）， 2018， 31（11）： 133-138.

[5]   MAURO VELARDOCEHIA. A methodology to investigate the dynamic characteristics of ESP and EHB hydraulic units[J]. SAE， 2006（1）：1281.

[6]  PAUL D， VELENIS E， CAO D. Tire road friction estimation based braking force distribution for AWD electrified vehicles with a single electric machine[C]// International Conference on Sustainable Energy Engineering and Application， IEEE， 2016： 82-87.

[7]  HER H， KOH Y， JOA E， et al. An integrated control of differential braking， front/rear traction， and active roll moment for limit handling performance[J]. IEEE Transactions on Vehicular Technology， 2016， 65（6）： 4288-4300.

[8]  ZHU B， PIAO Q， ZHAO J， et al. Integrated chassis control for vehicle rollover prevention with neural network time-to-rollover warning metrics[J]. Advances in Mechanical Engineering， 2016， 8（2）：1-13.

[9]  LUA C A， GENNARO S D. Nonlinear adaptive tracking for ground vehicles in the presence of lateral wind disturbance and parameter variations[J]. Journal of the Franklin Institute， 2017， 354（7）：2742-2768.

[10]  余曼，趙炜华，吴玲，等.后轮独立驱动电动汽车横摆稳定性控制研究[J].微电机，2019，52（7）：45-51.

YU M， ZHAO W H， WU L， et al. Research on driving system construction and yaw stability control of rear axle independent drive electric vehicle[J]. Micromotors， 2019， 52（7）：45-51.

[11]  霍超.基于相平面分析的汽车ESP模糊控制策略研究[D].长春：吉林大学，2012.

HUO C. Research on fuzzy control strategy for automobile ESP based on phase plain analyzing[D]. Changchun： Jilin University， 2012.

[12]  刘伟.汽车ESP系统控制策略研究及硬件在环验证[D].合肥：合肥工业大学，2017.

LIU W. Research on ESP control strategy and hardware in the loop verification[D]. Hefei： Hefei University of Technology， 2017.

[13]  严运兵，张振宇，许小伟，等.独立驱动电动汽车神经网络PID稳定性控制[J].机械科学与技术，2019，38（10）：1598-1605.

YAN Y B， ZHANG Z Y， XU X Y， et al. PID control of independent drive electric vehicle stability based on neural network[J]. Mechanical Science and Technology for Aerospace Engineering， 2019， 38（10）：1598-1605.

[14]  张伟超，赵华，杜铁，等.基于MFI理论的BWIM系统车辆轴重识别研究[J].公路工程，2019，44（2）：240-247.

ZHANG W C， ZHAO H， DU T， et al. Identification of axle weights of moving vehicles with BWIM system based on MFI theory[J]. Highway Engineering， 2019， 44（2）： 240-247.

[15]  张阿敏，吴汉立，马鹏飞，等.BWIM系统应用于正交异性钢桥面的整体效应分析[J].公路工程，2017，42（6）：261-267.

ZHANG A M，WU H L，MA P F，et al. The global effect of the applicatin of BWIM system to orthotropic steel decks[J].Highway Engineering，2017，42（6）：261-267.

[16]  余志生.汽车理论[M].北京：机械工程出版社，2012.

YU Z S. Automobile theory[M]. Beijing： Mechanical Engineering Press， 2012.

[17]  桑楠，魏民祥.车辆主动前轮转向与直接横摆力矩自适应控制[J].交通运输工程学报，2016，16（3）：91-99.

SANG N， WEI M X. Adaptive control of active front steering and direct yaw moment for vehicle[J]. Journal of Traffic and Transportation Engineering， 2016， 16（3）：91-99.

[18]  全国汽车标准化技术委员会. QC/T 480-1999.汽车操纵稳定性指标限值与评价方法[S].北京：中国标准出版社，1999.

National Automotive Standardization Technical Committee. QC/T 480-1999. Criterion thresholds and evaluation of controllability and stability for automobiles[S]. Beijing： China Standard Press， 1999.

[19]  全国汽车标准化技术委员会. GB/T 6323-2014. 汽车操纵稳定性试验方法[S].北京：中国标准出版社，2014.

National Automotive Standardization Technical Committee. GB/T 6323-1994. Controllability and stability test procedure for automobile[S]. Beijing： China Standard Press， 2014.