海上风机吸力式桶形基础承载特性研究综述

毋晓妮，廖 倩，李 晔*

（1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 上海交通大学 船舶海洋与建筑工程学院，

上海 200240）

随着全球能源需求不断增加以及全球气候变暖，能源短缺与环境问题日益突出。寻求可持续替代能源、开展能源转型已成为各国政府应对能源问题的主要措施。作为一种储量丰富的清洁可再生能源，风能在全世界受到了广泛关注并得到迅速发展。目前，瑞典、丹麦、德国、荷兰、比利时、英国和爱尔兰等国已经建立了许多研发性海上发电项目[1]。海上风电行业从20 世纪80 年代开始发展，并且自2000 年以来迅速发展。截至2016 年12 月底，全球风力发电装机容量已达到486 790 MW。截至2017年12 月底，全球累计风电装机容量为539.1 GW[2]。根据全球风能理事会的《2016 年全球风电发展报告》，2016 年全球海上风电新增装机2 219 MW，虽然装机容量与2015 年同期相比下降了31%，但未来前景看好。英国是世界上最大的海上风电市场，在全球装机容量占比中英国约占36%，德国占29%，中国占11%。根据欧洲风能协会（EWEA）对欧洲海上风机装机容量的统计可知，目前欧洲海上风电总装机容量为15 780 MW，图1 为1994-2017 年欧洲海上风机累计装机容量统计图[3]。近年来，我国也加快了海上风电建设的步伐，装机规模连续5 a快速增长，截至2017 年底，我国海上风电累计装机容量已达279 万kW。离岸15～30 km 的海域可以获得更高质量的风力资源，这一区域风力资源的开发需要采用更大型的海上风机来提高成本效益。随着海上风电行业的逐步发展与海上风机技术的不断进步，目前已开发了大型兆瓦级风机，其叶片直径可达120 m，功率可达6 MW。这些大型的海上风机同时也对为其提供支撑的基础的承载能力与稳定性提出了更高的要求。

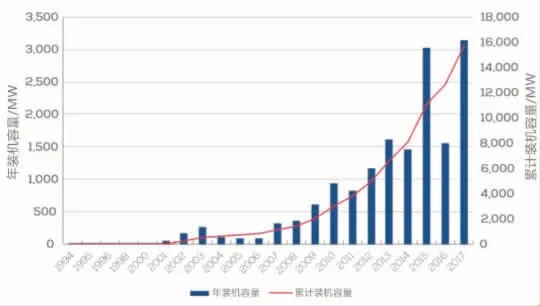
图1 欧洲风电装机容量统计图

海上风机基础在实际海洋环境中会受到复杂的海洋环境载荷的作用，这些荷载主要来自风、波浪和潮流。此外，在极端海况下，由于波浪砰击的作用，海水在风机基础表面上会有爬高，从而对风机的上层结构和设备造成威胁[4]。因此，与陆上风机基础相比，海上风机基础面临的环境更为严峻。此外，安装海上风机比陆上风机更加困难，并且安装与维护成本也更高，据统计海上风机基础设施的成本占风机总投资的34%[5]。因此，安全经济的基础设计也是海上风机能够正常长久运行的可靠保障，而基础设计已成为海上风电场设计的关键技术之一[6-7]。吸力式桶形基础由于其安装简单和可重复利用等优点，在海洋平台基础中得到了广泛应用，并逐步应用于海上风机基础中。但由于海上风机与海洋平台在海洋环境中的荷载工况有一定的差别，仍需要通过对其承载特性研究现状进行全面认识，以实现吸力式桶形基础在海上风机基础中的可靠应用。本文通过总结和评价国内外关于吸力式桶形基础的现有研究，综述了吸力式桶形基础在不同土体条件以及荷载条件下的承载特性研究现状，讨论目前应用于海上风机基础的吸力式桶形基础的技术难点和仍缺乏的研究，为海上风机吸力式桶形基础的可靠应用及后续研究提供重要参考。

1 海上风机支撑结构及基础分类

1.1 海上风机支撑结构及基础分类

海上风机的基础结构主要有6 种基本类型，其中包括重力式基础、单桩基础、三脚架基础、导管架基础、吸力式桶形基础以及组成浮式海上风机锚泊系统的各类锚固式基础。Malhotra[8]给出了不同类型的基础随水深的应用图示，见图2。其中，重力式基础（图2(a)）适用于水深小于20 m 的环境；单桩基础（图2(b)，(c)）的应用深度为5～25 m；三脚架基础（图2(d)）可以安装在15～40 m 的水深中；导管架基础（图2(e)）的安装水深为20～50 m；浮式风机锚泊系统（图2(f)，(g)）可以满足海上风机在大于50 m 的水深中正常工作的要求，该类基础虽然能够在深海水域为风机提供支撑，但是目前技术尚未成熟，仍在试验研究阶段[9]。

图2 海上风机基础随水深变化的典型应用

重力式基础通过风机自身的重力抵抗倾覆荷载。这类基础通常在下层海床中难以安装单桩基础时使用。当环境荷载相对较小且静载较大，或者当能够以合理的成本提供额外的压载时，重力式基础的经济效益较高[8]。而且重力式基础结构简单，安装方便。在安装重力式基础时离岸工作较少，无需打桩，对环境的影响较小。但是在大多数情况下，重力式基础在安装前需要对海床表层进行地基处理，并且其在使用的过程中需要考虑冲刷对基础结构稳定性的影响[9]。

单桩基础是一种外形简单的风机基础。单桩基础通常为大直径钢管桩，由大型冲击锤或振动锤打入海床，或者通过灌浆安装。沉桩后，在桩顶固定过渡段，然后将风机塔筒安装其上[10]。当单桩基础安装在较深的海上区域时，会出现挠度过大的问题，给基础的稳定性带来隐患，这个问题可以通过使用拉索（图2(c)）解决[8]。单桩基础结构简单、易于运输和安装。所以，目前单桩基础仍是海上风机中最常用的一种基础。其不足之处在于基础对海床的要求较高，并且安装时需要进行打桩[9]。作用在单桩基础上的竖向载荷通过表面摩擦和端阻力传递到土体中，作用在基础上的横向载荷会使基础产生弯曲变形后传递到土体中。因此单桩基础需要足够的刚度以抵抗水平向荷载，从而保证足够的稳定性以维持上部风机正常工作。这对单桩的直径提出了更大的要求。目前海上风机的单桩基础通常长30～40 m，直径3.5～6 m[11]。然而，过大的直径除了会在制造过程中带来困难外，也会使现有单桩基础设计采用的规范出现局限性，使单桩基础在水深较深海域的应用受到限制[12]，因此需要深入研究大直径单桩的力学特性并发展其设计方法。

三脚架基础的下部由细长三脚架构成，该三脚架构件可采用垂直或倾斜管，通过连接部分连接至中心桩，进而通过中心桩固定在海床上，为风机结构提供基本支撑。三脚架基础的支撑框架和中心桩一般在陆上建造并通过驳船运输到安装现场[8]。该基础与单桩基础类似，二者之间的区别在于荷载传递到海床的方式不同。三脚架基础所受到载荷可通过钢桩从主接头向下以轴向荷载的方式传递到海底，使得在满足同等承载条件下，三脚架基础比单桩基础更轻，在土中的安装深度更浅。此外，三脚架基础底座结构较大，具有更大的抗倾覆能力；其底座刚度更大，从而提高了基础的整体刚度；安装时无需任何海底准备。由于基座由相对细长的梁组成，因此允许水流相对无阻碍地穿过结构，从而减小水流对结构的影响。但是三脚架的基础结构复杂且制作成本较高，不同构件之间的接头处容易发生疲劳，这对结构的设计提出了更高的要求，三脚架基础的安装也比单桩基础更加复杂。此外，由于其结构体积较大，海上运输过程也极具挑战性[12]。

导管架基础属于“网格的三角架式基础”，组成基础的桩之间用撑杆相互连接，桩腿在海底处安装有轴套，桩通过轴套插到海底一定深度，导管架基础受到的荷载由打入地基的桩承担，从而使整个结构获得足够的稳定性。导管架基础强度高、底座大，可以提供更大的承载力及抗倾覆能力。与三脚架基础类似，导管架结构的空间框架结构允许水流穿过，减小了水流对结构的作用。但是导管架基础制造成本较高，制作时需要大量的钢材；基础安装时受天气的影响较严重；基础结构复杂，每个接头需经过特殊制造，需要大量工时完成焊接，而且连接点会存在应力集中以及腐蚀现象；此外，导管架结构由于体积较大，其运输也成为一个难题[9，12-13]。

在选择海上风机基础时，基础的成本是一个非常重要的考虑因素。在传统的海上风机基础中，重力式基础和单桩基础适用于水深较小的海域，当海上风场向水深较深的区域扩展时，这两种基础的制造成本会大大增加。而三脚架和导管架基础由于结构复杂、钢材用量大，除了成本较高以外，还存在焊接节点多、结构疲劳等严重问题。未来，随着海上风电场向深海领域的发展，传统的固定式基础将面临经济和安全的双重严峻挑战。

吸力式桶形基础是近年来从深海基础中逐渐发展起来的一种新型的海上风机基础，该基础是一种大型圆柱状钢制或混凝土薄壁结构，顶部封闭并设有排水抽气口，底部开口。与其他传统海洋基础相比，吸力式桶形基础具有安装方便、无噪音污染、抗倾覆承载力强、节省钢材并可重复利用等优点。预计该类基础将成为未来海上风机的基础形式之一。研究表明，吸力式桶形基础在施工期间易于运输和安装，可节省总成本的30%[7]。吸力式桶形基础海上风机示意图[14]如图3 所示。

图3 吸力式桶形基础海上风机示意图

1.2 海上风机吸力式桶形基础应用现状

吸力式桶形基础是由带顶盖的圆柱形钢板组成的，海上风机吸力式桶形基础长径比（L/D，其中L是桶长，D是桶体直径）一般在0.5～1 之间，通常小于吸力锚的长径比（最大为6）。目前有两种类型的桶形基础海上风机（见图4[15]），一种是单桶基础（见图4(a)）海上风机，另一种为多桶基础（见图4(b)）海上风机。单桶基础的直径通常为20～25 m，而多桶基础的直径为6～8 m。多桶基础主要通过承载一定的拉力或者压力来保持稳定，涉及到力的传递；而单桶基础则直接受到自身或来自环境的水平和竖向荷载，对其研究分析更具有代表性[15]，因此本文主要分析涉及单桶基础的现有研究。

图4 单桶基础式海上风机与多桶基础式海上风机示意图

吸力式桶形基础平均安装时间约为6 h，整个安装过程分为两步。首先，吸力式桶形基础靠自重和上部结构的重量插入海底一定深度，并且形成有效密封，之后再通过桶顶部预留的排水口抽出桶中的空气和水以形成负压，从而利用桶内外的压力差把基础驱入海底地层中的设计深度[16]。

吸力式桶形基础安装简单，无需进行打桩，也无需进行海床处理，因此安装较快，并且安装噪音较低，可以较好地降低施工和安装成本。吸力式桶形基础在使用结束时可以通过安装逆过程拔出，再运输到其他场地进行再次使用，从而可以实现基础的重复利用，节省资源。此外，吸力式桶形基础中所用到的钢材少于传统单桩基础，并且桶形基础的结构简单，可以实现大规模生产[17-18]。

2002 年，丹麦Fredefikshaven 的风电场建设首次使用直径12 m、高6 m 的吸力式桶形基础。此外，丹麦于2009 年在Horns Rev 2 风电场中成功安装了吸力式桶形海上测风塔，桶形基础的直径为12 m、长6 m[18]。2013 年2 月，两台吸力式沉箱基础的海上测风塔安装在英国Dogger Bank 水深为25 m 的海床上。2014 年8 月，DONG Energy 成功地在Borkum Riffgrund 1 离岸风场水深25 m 处安装了三脚架吸力式沉箱基础海上风机[19]。2018 年4 月，德国第一个海上风电场Borkum Riffgrund 2 中的8 MW 吸力式桶形基础的海上风机全部安装完毕，计划于2019年投入运行。2018 年10 月，瑞典Vattenfall 能源公司宣布将在苏格兰海岸阿伯丁湾（Aberdeen Bay）正式开通运营装机容量为93.2 MW 的阿伯丁湾海上风电场。该项目包括两台MHI Vestas V164 8.8 MW海上风机和其他9 台8.4 MW 海上风机，这些海上风机由多桶式基础支撑。2010 年6 月，中国道达海上风电研究院采用复合桶形基础海上测风塔成功地进行了海上的安装作业。2016 年12 月，一步式风机安装船“道达号”装载世界首台海上风机复合桶形基础及塔筒完成了各项实测检测，于2017 年1月在三峡新能源响水海上风电场顺利安装到位。

在来自波浪、水流和冰等的水动力荷载的作用下，风机支撑结构的响应与风机的稳定运行和基础的承载密切相关，因此风机结构的响应是海上风能研究与开发的一大关键力学问题[13]。与传统的吸力式海洋平台相比，吸力式桶形基础海上风机受到的水平荷载较大，这些水平荷载主要是由风、波浪和冰引起的，基础受到的竖向荷载较小，其主要来源于结构的自重[20]。在极端条件下，吸力式桶形基础受到的水平载荷会达到所受竖向载荷的约60%[15]。因此，低竖向荷载与高水平和弯矩荷载是吸力式桶形基础海上风机设计中的重要考虑因素[21]。当基础受到外界荷载时，会发生沉降和转动，从而影响上部风机结构的正常工作，因此对其承载力进行研究对确定基础的稳定性至关重要[22]。目前，研究人员通过试验和数值模拟，对砂土和黏土中桶形基础在单调荷载和循环荷载作用下的承载力等问题进行了研究。

当基础所受到的最大荷载超过地基的极限承载力时会引起地基破坏，因此研究吸力式桶形基础的承载力和失效机理对优化桶形基础的设计标准和计算方法至关重要，其研究成果可以应用到工程实践中[13-14]。研究人员进行了实验室试验、现场试验、离心试验及数值模拟，以研究吸力式桶形基础在水平或竖向静荷载以及循环荷载下的承载力及行为特征及其影响因素。研究表明，不同条件下桶形基础的承载力受到多种因素的影响，包括基础的长径比、荷载幅值、加载频率、土体性质、基础的安装方式等[23-42]。

2 海上风机吸力式桶形基础研究现状

目前针对海上风机吸力式桶形基础的研究多为关于基础的承载力分析，主要涉及土体与结构物相互作用问题。所采用的研究方法主要有理论分析、数值模拟以及试验。目前在对桶形基础承载力研究的理论分析法中，用到最多的是极限平衡法和极限分析法。极限平衡法作为一种用来近似求解土力学稳定问题的传统方法，具有模型简单、公式便捷、易于理解等优点，因此极限平衡法在实践中得到了广泛的应用。然而，极限平衡法无法得到所假设的破坏面两侧的任意位置的应力分布。而且根据极限分析的理论可知，通过极限平衡方法所得到的承载力既不是上限解也不是下限解，无法给出真实解的范围，因此学者们发展了具有严密理论基础的极限分析方法来对桶形基础的极限承载力进行分析。对吸力式桶形基础进行的试验主要包括离心试验、现场试验和实验室试验。现场试验测量数据较为方便，但是需要投入相当大的费用和时间[23-24，43]。实验室试验较为经济，并且容易更改试验参数，如土体的性质和基础的尺寸等，但是通过实验室试验测得的数据需要经过处理还原之后才能应用到实际工程当中[25-31]。在小规模试验中，离心机试验可以实现模型基础与原型基础相应点上的有效自重应力相同，使原型的特性可以在小尺寸模型中再现。并且重复试验可以降低试验成本，这也是国内外大量开展离心机试验研究的原因[44-45]。但是由于试验所能研究的问题范围较为有限且成本较高，许多学者通过ABAQUS、Z_SOIL[19]、PLAXIS[46]、FLAC[47]等软件使用有限元方法对相关参数进行更广泛而全面的研究。本文将对海上风机吸力式桶形基础的静承载力、循环荷载响应等相关问题展开讨论，对已有的关于试验及数值模拟研究进行介绍与分析。

2.1 海上风机吸力式桶形基础静荷载承载力研究

对海上风机吸力式桶形基础的静荷载承载力研究主要包括基础的竖向静承载力和水平静承载力。

海上风机吸力式桶形基础结构受到的竖向荷载主要来源于结构的自重，与其他桶形基础式海洋平台相比，吸力式桶形基础式海上风机自重较小，因此基础受到的竖向荷载相对于其他桶形基础式海洋平台而言也较小。竖向荷载下桶形基础的研究背景可概括为以下两点：第一，在设计多桶联合基础时，将上部结构受到的水平荷载和弯矩有效地传递到基础中是一个重要的考虑因素，通过改变下部多桶基础与上部结构连接构件的刚度，来自上部结构的荷载会被均匀地传递到多桶基础上，部分桶形基础承受压力，部分桶形基础承受张力，从而与上部结构受到的自重与水平方向荷载平衡[26]；第二，桶形基础在安装和拔出的过程中会受到较大的竖向荷载，同时上部风机结构受到的水平荷载会导致基础受到大的力矩的影响，此时需要通过基础上部土压力和基础的竖向承载能力来确保整个吸力式桶形基础海上风机的稳定性[28]。因此，研究桶形基础的竖向承载力对基础的正常工作和稳定性具有重要意义。此外，在竖向循环荷载作用下的桶形基础的研究中，通过试验先得到基础在竖向静荷载作用下的承载力，取竖向静荷载的80%作为竖向循环荷载加载值[26]。目前已有的关于桶形基础的竖向静承载力及其影响因素的研究中，研究人员通过试验或者数值模拟得到桶形基础的荷载-位移曲线、荷载-孔隙水压力曲线以及土体的破坏模式，并对得到的结果进行分析讨论。通过研究可以发现，桶形基础的静承载力主要受到基础的长径比、基础的安装方式和土体的性质的影响[28，36-39]。

2.1.1 竖向静承载研究 研究人员对桶形基础的竖向承载力进行了相关的试验研究[26，40，48-49]。Liu 等[40]、孙大鹏等[48]对海上风机吸力式桶形基础进行了试验研究，探索了桶形基础与软土地基的相互作用机理，并且研究了桶形基础在竖向荷载作用下的软土地基承载力情况，从而确定桶形基础地基的破坏模式。通过对土体的变形分析可知，当桶形基础受到竖向荷载作用时，由基础桶裙内部的土体与基础一起承受载荷作用，裙底部附近的土体发生塑性变形。当桶形基础所受的竖向荷载大于地基的极限承载力时，桶形基础下的地基土发生整体剪切破坏。Vaitkun 等[26]通过试验求得砂土中海上风机吸力式桶形基础的竖向静承载力，得到的结果作为循环试验中施加的循环荷载的幅值选区的参考依据。为了深入探讨吸力式桶形基础结构与地基的复杂相互作用和基础的承载力及其影响因素，有限元等数值分析方法得到了广泛应用。Park 等[42]基于遵循非关联流动准则的摩尔-库伦模型研究了砂土中桶形基础的竖向荷载传递机理，通过轴对称有限元分析法计算了砂土中桶形基础的桶壁摩擦力和基础承载力，并且提出了二者的计算公式。Hung 和Kim[38]根据三维有限元数值模拟结果提出了黏土中桶形基础的竖向承载力的计算公式：

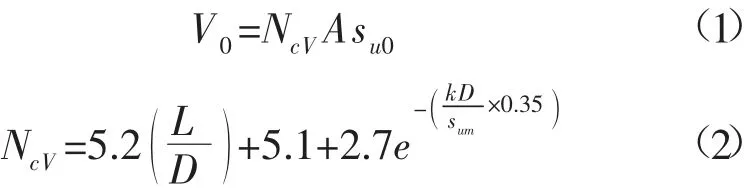
式中：NcV为基础的竖向承载力系数；V0为基础的竖向承载力；A为桶形基础的横截面积；su0为桶顶部以下D/4 处土体的不排水抗剪强度；sum为地表不排水抗剪强度；k为土体不排水抗剪强度随深度增加的比率。

徐赟[49]根据三维有限元数值模拟结果给出了桶形基础的竖向承载力计算公式：

式中：dcV为竖向埋深修正系数。

武科[50]提出，单桶基础的竖向承载力计算公式可以表示为：

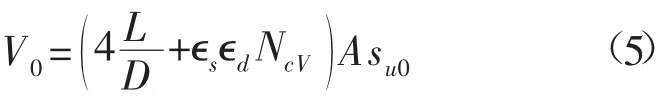
式中：NcV=2+π，为不排水土体的承载力系数；

Hung 和Kim[38]，Vulpe[51]等研究了黏土的非均匀性对桶形基础竖向承载力的影响，主要是通过试验和有限元方法研究不排水条件下土体强度对桶形基础的竖向承载力的影响。结果显示，黏土的非均匀性会影响桶形基础的竖向承载力，桶形基础的竖向承载力随着黏土的非均质性的增加而下降。Hung和Kim[38]给出了桶形基础的竖向承载力系数NcV（V0/Asuo）随土体不均匀系数kD/sum的变化曲线。Vulpe[51]通过数值模拟给出了桶裙基础在土体不排水抗剪强度（su=sum+kz，其中k取0，6，20，60，100）不同的土体中的竖向承载力系数NcV。

Hung 和Kim[38]，Vulpe[51]，Mehravar 等[39]，Barari 等

[28]研究了桶形基础的长径比对桶形基础承载力的影响。其中，Hung 和Kim[38]，Vulpe[51]和Mehravar 等[39]对黏土中的桶形基础进行了数值模拟，Barari 等[28]在砂土中进行了一系列试验和数值模拟，以估算砂土中桶形基础的竖向承载力。不同长径比的桶形基础的无量纲化竖向荷载-位移曲线如图5 所示。研究结果显示在砂土和黏土中得到的结论是一致的，桶形基础的竖向承载力随着基础长径比的增加而增加，由于桶形基础在竖向荷载作用下的失效机理会随着长径比的增加逐渐发生变化，基础的竖向承载能力的增加为非线性。Mehravar 等[39]根据有限元结果给出了竖向承载力系数的计算方法，并与已有的结果进行对比，对比结果如图6 所示。在研究中，Vulpe[51]计算的桶形基础长径比的取值范围为0～0.5，Mehravar 等

[39]及Barari 等[28]计算的桶形基础长径比的取值范围为0～1。目前在已有的关于桶形基础长径比对基础承载力的影响的研究中，基础长径比的取值范围大都在0～1 之间。考虑到未来对更高承载的桶形基础的要求，仍有必要对长径比大于1 的桶形基础进行试验研究和数值模拟，并提出相应的经验公式。目前已有的研究中给出的黏土中桶形基础的竖向承载力系数差别较大，尚未得到统一的结果，仍需要对不同参数条件下桶形基础的承载力系数进行深入研究。

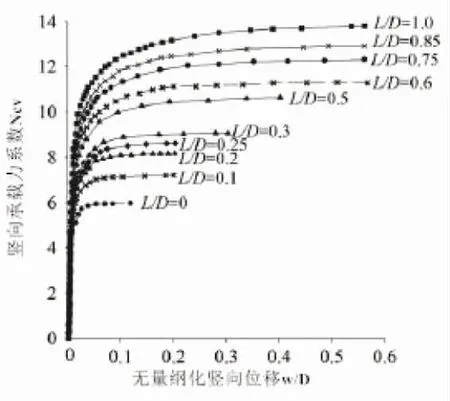
图5 不同长径比桶形基础的无量纲化竖向位移-荷载曲线[38]

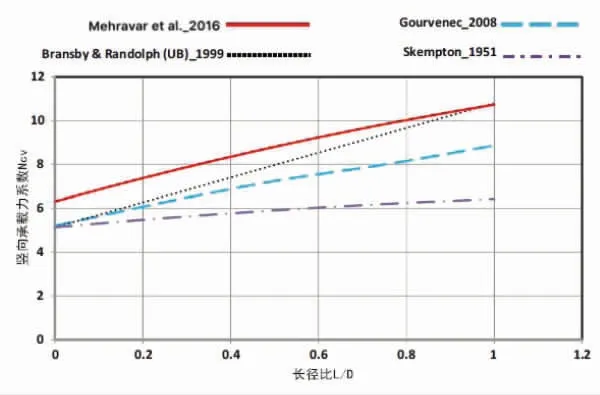
图6 不同竖向承载力系数计算结果之间的对比[39]

Vulpe[51]研究了基础与土体之间的接触对桶形基础承载力的影响，模拟了土桶之间存在摩擦与土桶之间光滑无摩擦这两种情况，得到了在这两种情况下桶形基础的竖向承载力系数。Park 等[52]通过轴对称有限元方法分析计算了安装在砂土上覆黏土的复合土体中的桶形基础的竖向承载力，并根据有限元计算结果提出了基于回归分析的竖向承载力预测方程。Zou 等[53]同样研究了砂土上覆黏土的复合土体中基础的承载力。二者的区别在于前者的桶形基础安装在砂土层中，而后者桶形基础则深入到黏土中，研究上层砂土的厚度对桶形基础竖向承载力的影响。

2.1.2 水平静承载研究 采用桶形基础的海上风机在正常的工作条件下受到的水平荷载主要是由风、浪等引起的，这些荷载会对桶形基础的稳定性产生不利影响，使基础平移或者转动。当基础的位移达到一定程度时会失去稳定，导致上部结构无法正常工作。因此研究在水平静荷载作用下桶形基础的承载力问题可以为海上风机的设计提供参考，从而保证海上风机的正常运行。研究人员研究了砂土和黏土中桶形基础在水平静荷载作用下的承载机理及相关问题，对桶形基础的水平承载力及其影响因素进行了试验研究和数值模拟，其中影响因素包括基础的长径比、土体的性质（如土体的固结程度、土体密度及土体的排水情况等）和竖向静荷载[16，25，33]。

孙大鹏等[48]、魏世好等[54]通过模型试验探索了桶形基础与软土地基相互作用机理，研究了桶形基础在水平荷载作用下的软土地基承载力情况，确定桶形基础地基的破坏模式。基础在受到水平荷载作用时会发生平动和转动，而这两种运动形式最终会导致地基的破坏。桶内壁前侧和后侧土压力随着水平荷载的增加而变化并不显著，只在桶体底部才有所改变。桶外壁前侧土压力在接近桶底之前随着水平荷载的增加而增大，然而在接近桶底部时，由于土压力从被动土压力转为主动土压力，导致土压力先减小后增大。当水平荷载增大到一定程度时，桶体外壁与地基土接触区域产生裂缝，从而造成桶外壁外侧土压力降低；而在接近旋转中心处以下，土压力随着水平荷载的增加而增大[48，54]。

在试验的基础上，不少学者对桶形基础在水平方向的承载力进行了研究[55-57]。施晓春等[55]在模型试验的基础上，考虑土压力的位移效应，提出了一种计算桶形基础水平承载力的近似方法。计算结果表明，该方法计算所得到的桶形基础水平承载力与试验结果吻合较好。Sukumaran 等[56]采用有限元分析方法求解软黏土中吸力式桶形基础在不排水条件下的承载力。基于实际破坏模式的三维特性，采用加密的三维的模型进行分析，并提出用准三维的傅里叶分析代替真三维分析，从而改善计算效率，二者结果符合很好，该有限元方法己由经典的极限解证实。Wang 等[57]通过极限平衡法建立偏心水平承载力公式，在偏心水平承载力计算的有限元分析结果的基础上，建立了水平荷载和弯矩荷载作用下单桶基础偏心水平荷载计算方法。Zhang 等[58]提出了一种基于上限理论的海上平台吸力式桶形基础稳定性的三维极限方法。范庆来等[59]针对横观各向同性软基上深埋式大圆筒结构的水平承载力，提出了一种改进的极限分析上限解法。Hung&Kim[38]根据模拟结果提出了黏土中桶形基础的水平承载力的计算公式：

式中：H0为基础的水平承载力；A为桶形基础的横截面积；L为桶形基础的长度；D为桶形基础的直径；su0为桶顶部以下D/4 处土体的不排水抗剪强度；sum为地表不排水抗剪强度；k为土体不排水抗剪强度随深度增加的比率。其中，NcH是基础的水平承载力系数。

徐赟[49]根据三维有限元数值模拟结果，也给出了桶形基础的水平承载力计算公式：

式中：参数的意义与式(6)～式(7)中相同。

武科[50]提出单桶基础的水平极限承载力经验公式可以表示为：

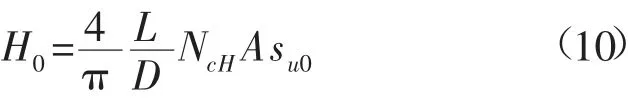
式中：参数的意义与式(6)～式(7)中相同。

桶形基础水平方向的承载力受到许多因素的影响，目前已对不同的因素展开研究。Mehravar 等，Hung 等通过试验和三维有限元方法对桶形基础长径比对水平承载力的影响进行了研究[38-39，60]。通过试验和数值模拟得到桶形基础的荷载-位移曲线并对其进行分析，结果表明，与竖向承载力相似，桶形基础的水平承载力会随着基础长径比的增加而逐渐增加。单桶基础的水平承载力系数目前有两种计算方式，一种为NcH=H/(Asu)，另一种表达式为NcH=H/(LDsu)。其中，H为基础的水平承载力；A为桶形基础截面面积；L为基础长度；D为基础直径；su为土体不排水抗剪强度。Mehravar 等[39]给出了不同长径比的桶形基础的荷载-位移曲线（见图7[38]）和水平承载力系数与桶形基础长径比之间的关系（见图8[39]），并根据有限元结果给出了水平承载力系数计算公式且与已有的结果进行对比。Lee 等[60]通过试验研究发现，桶形基础的破坏模式会随着基础长径比的变化而变化。长径比为1 的桶形基础在发生破坏时，基础在水平静荷载的作用下会产生水平移动和旋转两种位移，基础前侧的土体变形较大。而长径比为0.5 的桶形基础在水平静荷载的作用下只发生转动，基础前侧的土体变形较小。Liu 等[25]通过对桶形基础进行试验得到了类似的结论，进一步提出宽浅桶形基础的水平极限承载力的倾角约为3.0°。当桶形基础的长径比小于0.5 时，基础的水平极限承载力对应的倾斜角约为3.0°，转动中心位于土体表面下方0.5L的高度处。当桶形基础的长径比大于0.5 时，基础的水平极限承载力对应的倾斜角小于3.0°，转动中心位于土体表面下方0.7L的高度处，其中L为基础长度。目前已有的研究中给出的黏土中桶形基础的水平承载力系数也不尽相同，不同研究得到的结果差别较大，所以仍需要对不同参数条件下桶形基础的承载力系数进行进一步研究。

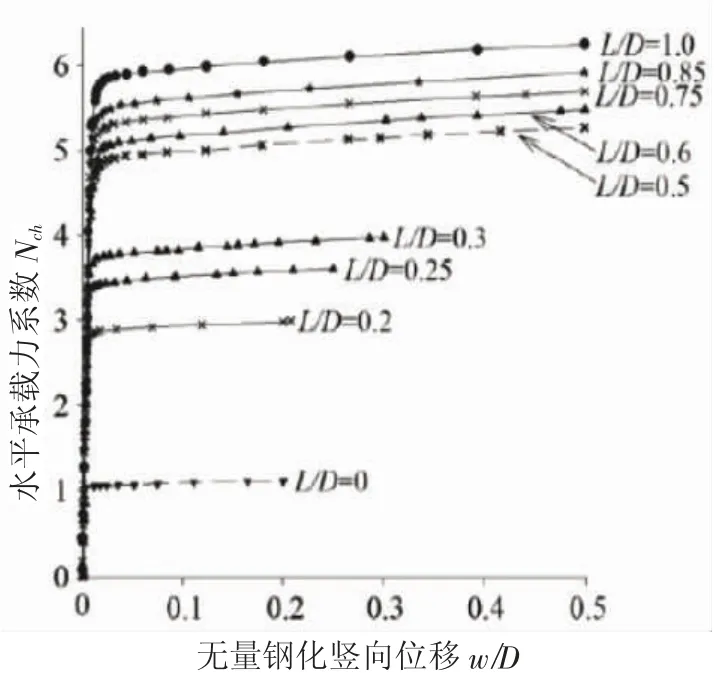
图7 不同长径比桶形基础的无量纲化水平方向位移-荷载曲线

图8 不同水平承载力系数计算结果之间的对比

有学者对土体性质对桶形基础承载力的影响进行了研究[38]。Wang 等[61]采用50 g 离心试验研究了土体的固结程度对桶形基础水平承载力的影响，结果表明土体的固结程度对桶形基础的水平承载力影响显著，通过试验所得结果可以看出，重度超固结土体中桶形基础的水平承载力明显大于轻度超固结土体中桶形基础的水平承载力。Hung 和Kim[38]研究了黏土的非均匀性对桶型基础承载力的影响，通过数值模拟给出了水平承载力系数H0/Asu0随土体不均匀系数kD/sum的变化曲线，研究发现黏土的非均匀性对桶形基础的水平承载力具有较大影响，桶形基础的水平承载力随黏土的非均质性的增加而下降。

Choo 等[34]通过70 g 离心试验研究粉砂土的排水条件对海上风机吸力式桶形基础水平承载力的影响，通过试验得出在土体塑性区，不排水条件下基础的水平承载力大于排水条件下基础的水平承载力。Liu 等[41]通过三维有限元模型分析竖向荷载对海上风机吸力式桶形基础的水平承载力的影响，结果显示，在桶形基础上施加一定的竖向荷载，会增加基础的水平承载力，桶形基础的长径比越小，增加竖向荷载对基础水平承载力的提高越明显。

2.1.3 复合荷载承载研究 除了对桶形基础在竖向或水平单向荷载作用下的研究，有学者对复合荷载下桶形基础的承载力问题也进行了研究，对研究得到的竖向荷载、水平荷载和弯矩荷载进行无量纲化，分别得到V/Asu，H/Asu和M/ADsu。其中，A为基础横截面积；su为土体不排水剪切强度；V为基础的竖向承载力；H为基础的水平承载力；M为基础的弯矩承载力[16，38，51，62-64]。根据所得结果给出桶形基础的破坏包络面图（见图9[37]）。破坏包络面是研究复合荷载作用下桶形基础地基极限承载力的一种有效的方法。若荷载组合位于包络面外，则基础发生破坏；若组合荷载位于包络面内，则地基处于稳定状态。

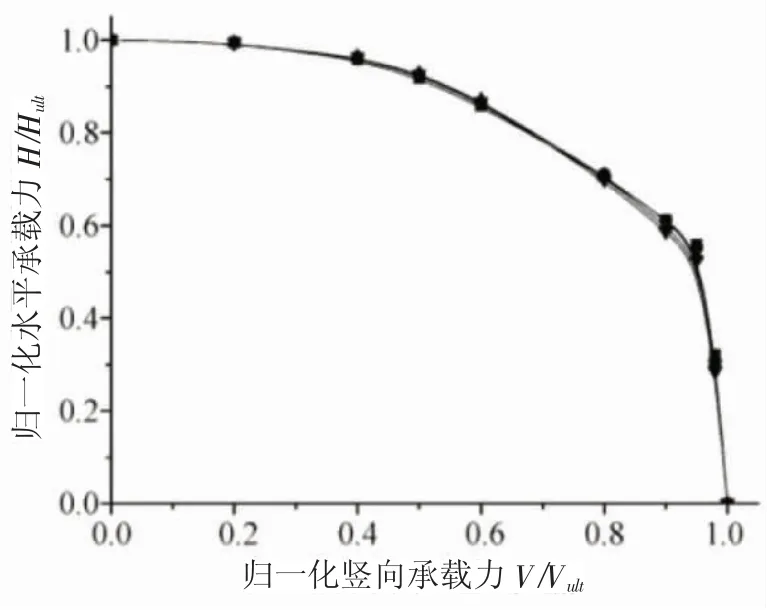
图9 归一化V-H 包络面

Gourvenec[62]，Hung 和Kim[38]，武科等[63]，Bagheri等[16]，Vulpe[51]，Aubeny[64]通过三维有限元方法研究了不同条件下桶形基础的破坏包络面，为桶形基础的设计和应用提供参考依据。通过研究表明，桶形基础在复合荷载作用下的承载力受到基础长径比、土体的固结程度、砂土的疏密程度、土体的非均匀性以及排水条件的影响。随着桶形基础长径比的增加，基础的破坏模式逐渐发生变化，基础的承载力也呈非线性增加。武科等[65]对复合桶形基础的承载特性进行了三维数值模拟，计算了在V-H，V-M，VH-M空间内桶形基础的破坏包络面，给出相应条件下破坏包络面的经验计算公式，用来评判实际荷载作用下桶形基础的工作状态。此外，Zou 等[53]研究了砂土上覆黏土的复合土体中砂土厚度对桶形基础承载力的影响，给出了V-H，V-M，M-H破坏包络面及相应的表达式。目前已有的关于桶形基础的破坏包络面的表达式只适用于长径比较小的浅基础，对于长径比较大的适用于深海的桶形基础的破坏包络面的表达式还有待进一步研究。

尽管目前对桶形基础的静承载特性研究较多，但是由于桶形基础在海上风机中的应用仍较为有限，为了将其可靠地应用于海上风机基础中，仍需要采用合理的三维有限元分析方法对一些问题进行深入分析，如长径比较大的桶形基础的承载特性，特定水平和竖向荷载组合下的吸力式桶形基础响应，土体应变软化现象对基础承载力的影响及基础安装效应对桶形基础承载特性的影响等。作为海上风机基础，除了需要满足地基基础的强度和稳定外，还要确保基础刚度满足整个风机-支撑结构-地基系统的频率响应要求，避免系统产生过大振动，保证风机正常安全运行。常有的拟静力分析可能难以确保结构设计的安全，需要采用合适的动力分析方法进行分析[13]。表1 给出了已有的关于吸力式桶形基础的研究总结表。

表1 吸力式桶形基础研究总结表

2.2 海上风机吸力式桶形基础循环荷载响应研究

在海上风机的设计寿命期间（通常为20～30 a），基础将受到不同循环荷载的作用，如水平循环荷载和竖向循环荷载。其中水平循环荷载来自风荷载、波浪荷载、流荷载、冰荷载等[27]。当海上风机的基础为多桶基础时，来自风和波浪等较大的水平荷载转移到每个基础上时会以竖向循环荷载的形式出现[26]。在高倾覆力矩和周期性水动力荷载的作用下，桶形基础周围土体的孔压累积，可能会使砂质海床发生液化或使黏土地基发生软化，软化后的海洋软土地基中桶形的基础承载力将显著降低。同时，由于循环荷载的作用，地基会发生较大的累积变形，从而发生失稳破坏。因此，在设计分析中考虑循环荷载作用下桶形基础的极限承载力可以为海上风机吸力式桶形基础的设计提供参考[66]。

目前已有相关研究通过考虑循环荷载的特征以及土体的循环软化效应来评估水平和竖向循环荷载下桶形基础的循环承载力。研究人员通过试验和数值模拟得到基础在循环荷载作用下典型的位移时间历史曲线、荷载-位移曲线、位移-循环次数曲线以及荷载-孔隙水压力关系曲线等结果来研究桶形基础的循环承载机理、基础的循环承载力及其影响因素，其中影响因素主要有在基础上施加的竖向静荷载、荷载的循环次数、基础的安装方式以及荷载的施加方式[67-72]。

为了考察循环荷载作用下饱和黏土的强度弱化对于重力式基础承载力的影响，Andersen 等[67-68]提出了软黏土的循环强度概念，将在一定循环次数下，当土单元达到变形破坏标准时，作用在剪切破坏面上的初始静剪应力和动剪应力之和定义为循环抗剪强度，并据此提出了拟静力极限平衡计算方法。Yasuhara 等[69]通过应力控制式的循环三轴试验和应变控制式的单调剪切试验，确定循环荷载作用下黏土的刚度衰退特性密切地依赖于单幅轴向应变或剪应变，与采用超静孔隙水压力作为评价参数相比，选择剪应变作为评价循环荷载作用下刚度衰减特性的参数更为合适。

2.2.1 竖向循环荷载响应研究 刘振纹[70]、李驰[71]通过土工试验探讨了软黏土循环强度的变化规律，在此基础上，把有限元方法和土动力试验得到的循环强度相结合，提出了拟静力Mises 弹塑性模型，建立了评价桶形基础地基循环承载力方法。Wu 等[72]提出了一种计算吸力式桶形基础竖向循环承载力的三维准静态有限元方法。Cheng 等[73]提出一种新的本构模型来模拟静荷载和循环荷载作用下黏土的应力应变响应，通过三维有限元方法研究了在竖向循环荷载作用下吸力式沉箱基础的位移随时间的变化过程，并将计算结果与试验结果进行比较。与极限平衡法和准静态方法相比，该方法不仅可以确定循环荷载的承载力大小，而且还可以分析软黏土循环荷载作用下的吸力式沉箱变形过程和破坏机理，更适合计算复杂边界条件下的三维问题。

目前已有研究对竖向循环荷载的幅值与竖向循环承载力之间的关系进行探讨。Villalobos 等[27]通过试验研究了循环荷载幅值对黏土中桶形基础的竖向循环承载力的影响，结果表明，若平均竖向循环荷载等于最大安装荷载，基础会发生永久沉降；若平均竖向循环荷载等于0，尽管当基础受压时会发生暂时性的沉降，但是最终会发生永久隆起。Wang 和Yang[74]在自制软土地基中对吸力式桶形基础进行了竖向循环加载试验，研究不同竖向静荷载对桶形基础竖向循环承载力的影响，并通过数值模拟对试验结果进行检验。试验结果表明，若基础受到的竖向循环荷载大于竖向静荷载，基础的竖向累积位移在初始阶段较大，之后的位移累积增长速率较小；若基础受到的竖向循环荷载小于竖向静荷载，基础的竖向累积位移值在初始阶段较小，之后的位移累积增长速率较大。此外，基础的竖向循环累积位移在初始阶段增长较快，随着时间的推移，循环次数的增加，竖向循环累积位移的增长速率逐渐减小。

Wu 等[72]研究了竖向循环荷载的循环次数对吸力式桶形基础极限承载力的影响，计算的荷载循环次数为0～2 000 次。其数值结果表明，黏土中吸力式桶形基础的竖向循环承载力小于基础的竖向静承载力，且随荷载循环次数的增大而减小。

目前关于砂土中桶形基础在竖向循环荷载作用下的试验主要针对的是竖向抗拔荷载，其应用背景为多桶基础，对于单桶基础在砂土中竖向循环荷载作用下的响应的研究较少。Emdadifard 等[47]使用二维有限元方法研究了砂土中竖向循环荷载作用下吸力式桶形基础的竖向循环承载力及基础长径比对其影响。通过模拟结果可以看出，桶形基础的竖向循环承载力随基础长径比的增加而增加。

2.2.2 水平循环荷载响应研究 桶形基础海上风机在正常工作条件下会受到波、浪等外界环境带来的水平循环荷载的作用，当土体受到循环荷载的作用时，孔隙水压力会急剧增加，土体应变会逐渐累积而导致其刚度退化。此时，基础和上部结构会在外界荷载的作用下逐渐发生转动，导致结构的固有频率发生变化，危及风机的正常运行。因此研究桶形基础在水平循环荷载作用下的承载力问题可以为实际工程建设提供参考依据[31，75]。

桶形基础水平循环承载力的研究主要包括基础的累积旋角、累积沉降、卸载刚度及其影响因素。闫澍旺等[76-77]通过离心机试验和动三轴试验研究了波浪荷载作用下软黏土地基波浪与地基的相互作用。Wang 等[61]采用50 g 离心试验研究了土体的固结程度对海上风机吸力式桶形基础水平循环承载力的影响，研究发现土体的固结程度对基础承载力的影响显著，重度超固结土体中桶形基础的水平循环承载力明显大于轻度超固结土体中桶形基础的水平循环承载力。

除了通过试验方法对桶形基础的水平循环承载力进行研究外，研究者们还通过数值模拟方法对桶形基础的水平循环承载力进行了研究[72，78-79]。Wu等[72]提出了一种计算海上结构吸力式桶形基础水平循环承载力的三维准静态有限元方法，研究了吸力式桶形基础在竖向循环荷载作用下的极限承载力。计算得到的数值模拟结果表明，由波浪载荷引起的土体循环软化效应会使桶形基础的循环承载力显著降低。Kourkoulis 等[78]采用非线性三维有限元分析，充分考虑了土桶之间的相互作用，研究了海上风机吸力式沉箱基础在水平循环荷载下的响应。文中提出了一种新的本构模型，该模型考虑了土压力的分布情况以及土桶之间的接触面强度对基础水平循环承载力的影响。Zhang 和Cheng[79]提出了一种基于热力学的本构模型，通过二维有限元方法来预测Bothkennar 黏土中海洋平台桶形基础在水平循环荷载作用下的沉降、转角、基础中孔隙水压力的发展和基础的刚度退化。模拟结果显示，在循环荷载作用下，地基中的孔隙压力和不可恢复的变形会不断累积。增加的孔隙压力会使得土体的剪切刚度和剪切强度降低，导致沉箱基础发生沉降和旋转。

有学者通过有限元方法研究了影响桶形基础水平循环承载力的因素，这些因素主要包括基础的长径比、土体的性质、荷载的幅值与循环次数、循环荷载频率、竖向静荷载以及冲刷坑等因素的影响[31，80]。循环荷载的幅值、加载频率和荷载循环次数对水平循环承载力的大小有着重要的影响[35，51，81-82]。Ding 等[82]通过数值模拟研究了荷载循环次数对砂土中海上风机吸力式桶形基础的水平承载的影响，模拟结果与黏土中荷载循环次数对桶形基础承载力的影响结果类似，结果表明，在水平循环荷载作用下，循环累积位移随循环荷载次数的增加而增加。Foglia 等[75]研究了加载频率对海上风机桶形基础在水平循环荷载作用下的长期累积位移的影响，试验结果显示，在测试范围内（0.025～0.1 Hz 之间），桶形基础的永久位移不受加载频率的影响。Lee 等[60]研究了黏土中单向荷载循环次数与循环荷载大小对基础承载力的影响，对固结高岭土中的桶形基础进行了高达10 000 次的单向水平循环荷载试验，试验结果如图10[51]所示。研究表明，桶形基础的累积转动随着水平荷载循环次数以及荷载大小的增加而逐渐增加，Zhu 等[81]和Cox 等[35]都通过试验研究得到了类似的结论。基于模型试验结果，Lee 等[60]提出了经验公式来计算黏土中单向循环水平荷载作用下桶形基础的累积转角θN和卸载刚度kN，计算公式为：

式中：θN为N次循环荷载后的累积转角；θ0为第一次循环荷载后的转角；Tb为考虑水平循环荷载率的无量纲参数；α 和β 为考虑周期数N和长径比L/D影响的参数；kN为N个循环后基础的卸载刚度；k0为初始卸载刚度；Ak为常数；N为荷载循环次数。

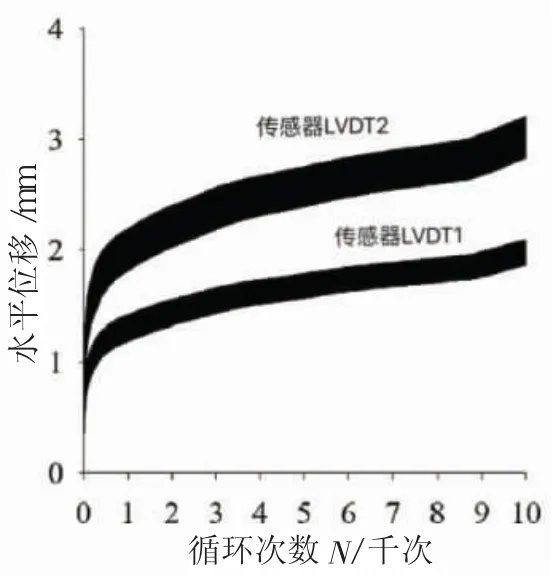
图10 水平循环荷载下的水平累积位移图（L/D=1）

王建华等[83]研究了竖向静荷载对桶形基础水平循环承载力的影响，对软土中的桶形基础在不同竖向静荷载与水平循环荷载组合下进行了模型试验。试验结果表明，导致桶形基础发生破坏的循环荷载幅值与循环次数取决于竖向静荷载，竖向静荷载越大，基础同一循环次数达到破坏时对应的循环荷载幅值就越小。

Chen 等[84]通过试验研究了冲刷对桶形基础稳定性的影响。结果表明，冲刷对砂土中吸力式桶形基础的稳定性有重要影响。随着冲刷深度的增加，基础的稳定性逐渐降低，基础的最终状态逐渐从循环稳定转变为循环失效，桶形基础转动中心的高度也随着冲刷深度的变化而变化。当冲刷深度较小时，基础的转动中心位于基础下部，距离基础顶部的距离为基础总高度的0.5～0.9 倍，基础转动中心的高度随冲刷深度的增加逐渐向下移动。

此外，Zhang 和Cheng[79]、Ding 等[82]研究了黏土中桶形基础的长径比对基础的水平循环承载力的影响。研究表明，当桶形基础的直径保持不变时，增加基础的长径比会提高基础的水平循环承载力，并且增大桶形基础的直径比与增加贯入深度更能提高桶形基础的水平循环承载力。Ding 等[82]还研究了水平循环荷载作用位置对砂土中海上风机吸力式桶形基础的累计位移和累积转角的影响。计算结果表明，随着水平循环荷载作用点的升高，基础的循环累积位移及累积转角都呈指数式增长。但是由于基础的旋转中心随着荷载作用点的升高而下降，所以基础在水平循环荷载作用下转角的增长幅度小于位移的增长幅度。

2.2.3 循环荷载响应研究小结 在对桶形基础进行循环加载试验时，大部分试验为了模拟基础在真实情况中遇到的波浪荷载，选取的循环荷载频率为0.1～0.5 Hz。对于循环荷载试验中循环荷载幅值的大小，一般会根据静荷载试验的基础竖向或者水平承载力来确定。虽然通过试验得到了一些关于桶形基础在不同荷载作用下的结论，但是仍存在一些问题需进一步探讨。第一，在实际情况中海上风机受到的环境荷载来自多个方向，并且循环荷载的幅值会随时间的变化而变化。前文提到的研究中选取的循环荷载是对实际荷载的简化，简化后的荷载均位于同一平面，并且在大部分试验中的循环荷载为简单的正弦曲线。此外，在大多数试验中循环荷载次数的量级为104，部分试验循环次数会高达106次，但是为了更加全面地验证所提出的方法，考虑到基础的疲劳极限状态以及海上风机在20 a 寿命中受到约108个周期的循环荷载的情况[35]，有必要进行循环次数更高的试验，如107个周期等[64]。第二，试验中需要考虑加载速率和排水的问题。若试验是在干砂中进行的，一般情况下无需考虑排水问题。但现场沉箱基础的规模较大，孔隙水难以在短时间内全部排出，特别是对于具有低渗透率的粉砂。这一问题可通过实验室试验或现场的大规模试验来解决，或者在小规模试验中改变孔隙流体的粘性，如使用更粘稠的流体（如硅油）代替水[81]。

对吸力式桶形基础在不同荷载作用下进行数值模拟时，通常会先对静荷载进行模拟计算，求得桶形基础在水平或者竖直方向的静承载力，为循环荷载幅值的选取提供参考。通过数值模拟研究得到的曲线和公式可用于实际海上风机的设计指导，但是模拟所得结果也存在一定的局限性：例如，在进行计算时会假设基础已经处于正确的位置，除非研究内容包含安装过程对桶形基础承载力的影响，否则一般不予考虑；对循环荷载进行数值模拟时计算的循环荷载周期较短，缺少对长期循环载荷的研究与计算；桶形基础在疲劳状态下的行为特征也需要进一步的研究。此外，通过数值模拟得到的有限元计算结果最好可以通过实验室试验、离心试验或者现场试验的验证[16]。

研究人员通过试验、理论分析和数值模拟等方法，研究了吸力式桶形基础在循环荷载作用下的响应及其影响因素，提出了不同的本构模型来模拟土体在循环荷载作用下的应力应变响应，通过计算得到基础的累积转角与累积沉降曲线，并对相关的影响因素进行分析。可知在循环荷载的作用下，基础的承载力会随着循环荷载次数的增加而降低，累积位移随着循环次数的增加而增加。基础的长径比会影响基础在循环荷载作用下的响应，桶形基础在循环荷载作用下的承载力会随着基础长径比的增加而增加[79，82]。

尽管目前已有关于桶形基础在循环荷载作用下的承载分析，但目前的分析多针对较短的循环周期，缺乏针对海上风机较长循环周期下的承载研究；同时缺乏合适的针对循环次数较大的土动力特性的本构模型，因此对海上风机桶形基础在循环荷载作用下的承载特性分析仍需要建立合理的本构模型，针对长周期循环次数较大的循环荷载响应问题进行合理分析。另外，应针对该部分规范缺乏的问题，提出海上风机桶形基础循环荷载下承载设计规范。

3 研究展望

海上风机吸力式桶形基础的承载力是基础在设计过程中面临的一个重要的问题，直接关系到风机结构的稳定性、安全性及可靠性。针对以上对各关键问题的研究现状分析，可知尽管现有的针对桶形基础的研究较广泛，但针对其在风机使用中所面临的不同的荷载工况，仍需要通过大量数值及试验研究对其进行深入研究，下一步可进行的研究主要包括以下几方面。

（1）目前已有的关于桶形基础的承载力研究针对长径比范围在0～1 之间的桶形基础，缺少关于较大长径比范围的桶形基础承载特性的研究。目前已有研究中对桶形基础施加的组合荷载较为简单，主要位于同一平面内，与真实环境中不同平面的组合荷载相差较大。因此，对海上风机桶形基础静承载特性的分析，仍需要采用合理的三维有限元分析，对较大长径比范围的桶形基础承载特性、风机在特定水平和竖向荷载组合下的基础响应，以及土体应变软化现象及基础安装效应对桶形基础承载特性的影响等问题进行深入分析，建立实用可靠的考虑多种土体条件及荷载条件下的承载力公式，为桶形基础在各类静荷载作用下的承载设计提供可靠的设计规范。

（2）对于海上风机桶形基础，需要联合研究机构与工业界，进行广泛的实验室试验及现场试验，提供可供数值方法及理论研究发展的有效数据，发展海上风机基础设计方法及工程设计模型，为海上风机吸力式桶形基础的有效利用提供可靠的设计方法及数据支持。

（3）目前已有的关于桶形基础在循环荷载作用下的试验研究和数值模拟的荷载特性都较为简单，最大荷载循环次数最多远小于实际情况中海上风机桶形基础遇到的循环荷载次数。对海上风机桶形基础在循环荷载下的承载特性分析，仍需要考虑风机实际循环荷载循环次数、循环荷载幅值变化、组合荷载及土体非均质性的影响，同时仍需要提出合理的本构模型及适用于工程设计的规范。

（4）海上风机将会遭遇复杂的海洋环境，包括海啸、台风等极端海洋环境事件更加值得关注，海上风机在恶劣环境下的响应的模型亟待研究与发展。

（5）针对采用桶形基础的海上风机结构分析，仍需要建立完整的、考虑实际上部风机结构、下部支撑结构、底部桶形基础及与土体相互作用（在复杂外部环境荷载作用下）的耦合分析，结合结构力学、水动力学及岩土力学知识，发展合理的可应用于工程设计的分析模型。

4 结语

本文综述了目前海上风电的发展现状，针对目前在海上风机各类基础中具有较好应用前景的海上风机桶形基础，重点综述和评价了桶形基础在各种荷载下的承载力研究现状，讨论了各部分研究所得到的重要结论，并展望了下一步可开展的研究。通过本文的调研，对目前桶形基础的承载特性研究及其在海上风机基础应用中所存在的问题及工程适用性有了全面的认识。文章概括了当前桶形基础核心力学问题的研究现状，明确了该类基础未来广泛应用于海上风机基础中仍需开展的深入研究工作方向。这些研究将有助于未来对海上风机桶形基础及其他各类海上风机基础研究工作的深入，直接有益于全球海洋基础工程在风电领域的技术发展，对我国海洋工程及海上风电工程的发展意义重大。