非线性感应加热模型的有限元方法
2020-04-16支越
支越
(中国传媒大学 数据科学与智能媒体学院,北京 100024)
1 引言
感应加热是一种加热导体材料(如金属材料)的方法。在工业中,感应加热广泛用于金属硬化,锻造预热。感应加热系统的基本组件包括感应线圈,交流电源和工件。将线圈与电源连接,电源为线圈提供交变电流,交变电流产生通过工件的交变磁场,利用交变磁场产生涡流,从而达到加热的效果。
感应加热的过程非常复杂,因此,对于感应加热模型的数学分析可以在设计过程中提供有效帮助。感应加热模型由电磁场方程和热传导方程组成。关于线性电磁材料的研究,文献[1]给出了各种数值计算方案,文献[2,3]讨论了磁热耦合问题的适定性,给出了理论结果。
文献[4]中要求矢量势A满足无散性,然而文中假设电导率是与温度有关的函数,这与-∂tA无散的性质矛盾。在本文中,通过引入引入矢量势A,满足E=-∂tA,不考虑矢量势A无散度的条件,这样可以避免文献[4]理论中出现的矛盾;热传导方程中选用与文献[4]相同的Neumann边界条件。本文将给出非线性感应加热模型的势场公式。
2 模型简介
在涡流区域,麦克斯韦方程组[5]如下:
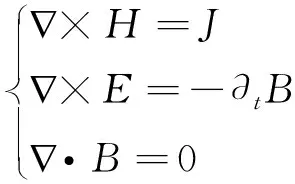
其中,E是电场,H是磁场,J是总电流密度,B是磁感应强度。
假设H与B之间的非线性关系[4]为
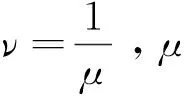
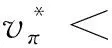
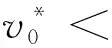
假设电导率σ=σ(u)依赖于温度函数u,σ是严格正的且有界,即存在常数σmin,σmax,使得0<σmin≤σ≤σmax<∞。
在麦克斯韦方程组中,由B的无散性,可以定义一个矢量势A,令B=∇×A,使得∇×(E+∂tA)=0,E=-∂tA。
工件上的感应电流密度为σπE,令Js为线圈中给定的源电流密度,其是Lipschitz连续的。考虑下述电磁场的初始边值问题:
σπ∂tA+∇×νM(∇×A)=Js,(x,t)∈Ω×(0,T]
A(0)=A0,x∈Ω,t=0
n×A=0,(x,t)∈∂Ω×(0,T]
其中A0∈H0(curl,Ω),Js∈L2(T),n是∂Ω上的单位外法线向量。矢量势M满足下列条件
M(0)=0,(M(x)-M(y))·(x-y)≥cM|x-y|2,cM>0,∀x,y∈3
|M(x)-M(y)|≤CM|x-y|,CM>0,∀x,y∈3
工件上的局部焦耳热为J·E=σπ|E|2=σπ|∂tA|2。焦耳热项在模型的分析中会产生许多问题,对其引入截断函数[4]
其中r是正的常数。温度函数的变化由下述非线性热传导方程表示:
∂tβ(u)-∇·(λ∇u)=Rr(σπ(u)|∂tA|2),(x,t)∈π×(0,T]
u(0)=u0,x∈π,t=0
其中,非线性函数β是连续的,导热系数λ是严格正的,有界的,满足
β(0)=0,|β(x)|≤Cβ(1+|x|),0<β≤β'(x),Cβ>0,∀x∈,
0<λmin≤λ≤λmax<∞,|λ(x,t2)-λ(x,t1)|≤Cλ|t2-t1|,Cλ>0,∀x∈π,∀t1,t2∈[0,T]。
3 变分形式
首先给出下文中要用的基本空间及基本定义。
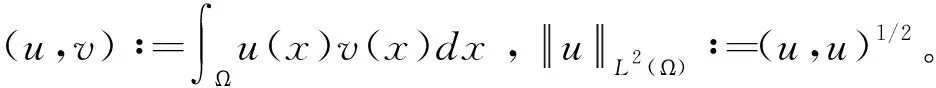
Hm(Ω)空间的范数:
其中m是非负整数,ξ表示非负三重指数。使用黑体表示向量值空间,如L2(Ω)∶=(L2(Ω))3。
变分空间及范数的定义如下:H(curl,Ω)={Q∈L2(Ω):∇×Q∈L2(Ω)},
应用上述定义,电磁场方程和热传导方程的变分形式为:
(σπ∂tA,Q)π+(νM(∇×A),∇×Q)π=(JS,Q)Τ,∀Q∈H0(curl,Ω),
(σπβ(u),ψ)π+(λ∇u,∇ψ)π=(Rr(σπ|∂tA|2),ψ)π,∀ψ∈H1(π).
4 时间离散化
设n是一个正整数,将区间[0,T]均匀剖分成n份,其中时间步长为τ=T/n,令
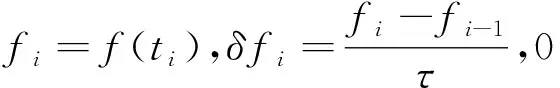
时间半离散格式为:
(σπ(ui-1)δAi,Q)π+(νM(∇×Ai),∇×Q)Ω=(JS,i,Q)Τ,∀Q∈H0(curl,Ω),
(δβ(ui),ψ)π+(λi∇ui,∇ψ)π-(Rr(σπ(ui-1)|∂tAi|2),ψ)π=0,∀ψ∈H1(π),
在上式中,σπ(u)取上一个时间步ui-1的值,这样处理可以求解Ai和ui,并不影响收敛结果。
使用单调算子引理[7],能够证明时间半离散格式解的存在唯一性。关于Ai和ui的稳定性估计,证明过程较为简单,证明思路类似文献[4]。
5 半离散格式收敛性
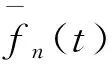
时间半离散格式的等价形式如下:
6 结论
本文讨论了一个感应加热模型,并提出其势场公式。在电磁场方程中,将电场化为矢量势形式。使用向后欧拉法,得出时间半离散格式。关于时间半离散格式的收敛性,其证明过程较复杂,证明思路类似于文献[4]。
