基于虚拟同步机的改进双馈风电机组控制策略研究

孟子立，王灵梅，姜齐荣，司荣国，鲍玉涛，尚立虎

（1.山西大学 自动化系，山西 太原 030013； 2.山西省风电机组监测与诊断工程技术研究中心，山西 太原030013； 3.清华大学 电力系统及发电设备控制和仿真国家重点实验室，北京 100084； 4.青海省绿色发电集团股份有限公司，青海 西宁 810001； 5.同煤集团 漳泽电力股份有限公司，山西 太原 030006）

0 引言

近年电网中风电的装机容量和接入比例得到了提升。 双馈风机 （Doubly-Fed Induction Generator，DFIG）因其运行稳定、成本低廉，已成为主要采用的发电方式之一。 目前风电机组大多采用最大功率追踪 （Maximum Power Point Tracking，MPPT）模式为电网输送电能，这使得风机的转速与电网的频率完全解耦，风电机组不再为电网提供惯量，加剧了电力系统的电力电子化特征，给电网的稳定运行带来了影响[1]～[4]。

同步发电机可以参与调节系统的频率、电压，因此，通过改进电力电子器件的控制策略使其拥有类同步机的外特性成为研究重点[5]。 文献[6]，[7]在 虚 拟 同 步 机 （Virtual Synchronous Generator，VSG）控制结构基础上，进行了功能性的改进。 目前关于虚拟同步机的研究主要侧重于其在微电网和光伏系统并网的应用[8]～[11]，而针对DFIG 发电系统的虚拟同步并网研究相对较少。

为了提升风力发电机组对于系统的响应，文献[12]通过修改最大功率追踪曲线的控制策略，使风机参与电网的频率响应，虽然为系统提供了一定的安全裕量，但降低了风机的发电功率。 文献[13]将虚拟同步机与风电机组网侧变流器控制结合，提出通过改变网侧变换器直流电压参考值，释放电容中储存的能量，充分利用了背靠背PWM换流器中直流电容储存的能量，但并未真正挖掘风轮机转子的能量。文献[14]将虚拟同步机运用于直驱风力发电机，提出风力发电机-同步电动机-同步发电机的两段式虚拟同步控制策略，但直驱型风机采用永磁同步电机作为发电机，属于全功率变换型风机，与DFIG 机组的控制存在本质区别。 文献[15]提出了运用于DFIG 机组的虚拟同步控制，但未引入电流内环控制，忽略了暂态电流过冲的可能性。文献[16]提出了基于转子磁链定向的双馈风机虚拟同步机控制，但被测量较多，易造成因测量不准带来的控制问题。 关于DFIG 的虚拟同步控制还有待进一步研究。

本文设计了一种基于虚拟定子电压定向的DFIG 风机变换器新型控制策略，通过将同步电机的转子运动方程与风机变流器控制相结合，成功将DFIG 的有功与无功分量解耦，并加入用于改良系统特性的惯性和阻尼模块，使变流器出口具有和同步发电机一样的外特性，为系统提供了有功、无功支撑。 该控制结构简单，仅需要测量定子侧电流、电网电压和转子位置角，同时电流内环控制的引入可避免暂态电流过冲。 最后，在PSCAD/EMTDC 平台上搭建了DFIG-VSG 模型，对所提出的控制策略进行了仿真，验证了控制策略的有效性与可行性。

1 虚拟同步控制的数学模型

虚拟同步控制是通过改进电力电子变换装置，以实现变流器的类同步发电机运行。选用二阶同步电机模型作为参考对象，综合考虑同步电机的电磁转矩和机械转矩，在变流器中重构转子的运动方程，对原本存在于实际同步电机中的调速器和励磁器进行复现，最终使变换器的输出电压、电流、功率与同步发电机相一致。 虚拟同步控制的转子运动方程和励磁调节方程分别为

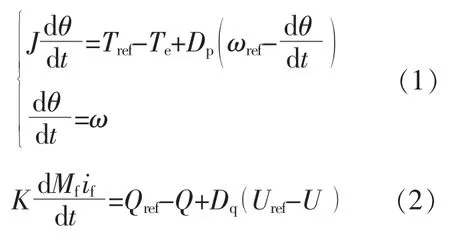
式中：J 为虚拟同步控制的虚拟惯量常数；θ 为虚拟转子角度；K 为比例系数；Te为电磁转矩；Tref为电磁参考转矩；Dp和Dq分别为频率和电压的阻尼系数；ω 为虚拟同步机虚拟电角速度；Mfif为虚拟直流励磁；ωref为电网同步电角速度；Uref为交流参考电压；U 为并网点电压。

结合式（1），（2）可得 VSG 的基本控制框图，如图1 所示。

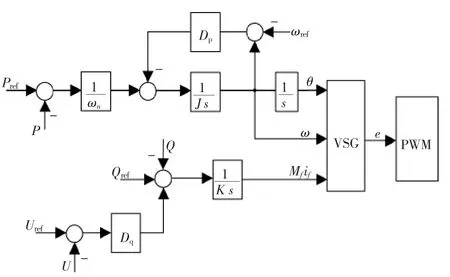
图1 虚拟同步机控制策略Fig.1 Virtual synchronous control structure diagram

由图1 可知，在VSG 的控制方程中，隐含着对于电网频率的自动追踪，但其自身又构建了类似同步电机旋转元件的相对独立的转速体系，也就是同步电机的功角。

通过模拟同步电机的数学模型，VSG 控制在电力电子变流器中实现了随电网电压和频率的变换，动态调整变流器的输出功率功能，重新建立了有功与频率、无功与电压之间的耦合关系，为系统提供相应的阻尼与惯量。

2 风力机模型

为了最大限度的利用风能，DFIG 变流器通常采用最大功率追踪控制策略，风轮机吸收的功率为

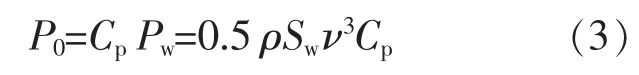
式中：Pw为风力机的输入功率；P0为风力机输出的机械功率；Sw为风机叶轮扫过的面积；ν 为当前风速；Cp为风能利用系数，其取值受到叶尖速比λ和桨距角β 的影响。

风轮机能够利用的最大风能为

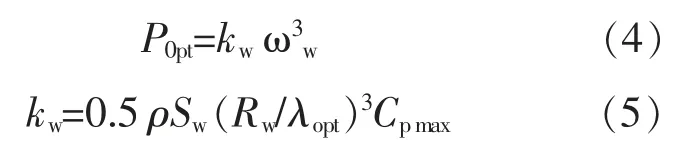
式中：ρ 为空气密度；Rw为风轮机半径；ωw为风轮机转速；λopt，Cpmax分别为当前风速下的最佳叶尖速比、最大风能利用系数。

在不同风速下，DFIG 风轮机都有最佳转速与之对应，如图2 所示。

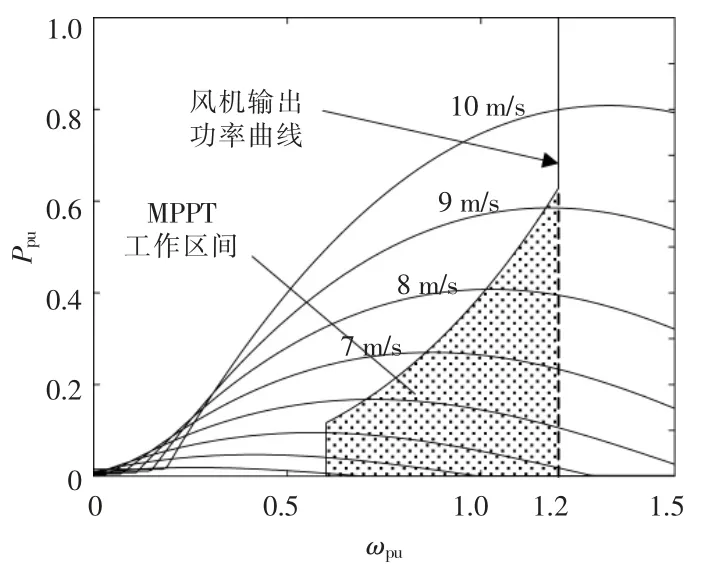
图2 不同风速下风力机的输出曲线和最大风能曲线Fig.2 Output power of wind turbine under different wind speeds & MPPT curve

由图2 可知，当风速由3 m/s 增加至10 m/s时，随着风速的提升，相同转速下的输出功率逐渐提高。 本文风力机使用MPPT 控制策略的输出功率曲线在图中由粗实线标出。 按照每台风机的最大风功率曲线设定风机并网点的输出参考功率，可实现风力发电机的MPPT 控制，图中粗细实线的交汇点即为风力机在对应风速下的稳态工作点。本文主要考虑最大风功率追踪区的控制（图中阴影部分），在此区间内，风力机桨距角不发生变化，风机运行于定桨距状态，故将风速设定在3～9 m/s。

3 改进DFIG型风力发电机控制

本文将VSG 控制与DFIG 型风机变流器相结合，提出一种基于虚拟定子电压定向的DFIG型风机控制策略。DFIG 型风机采用绕线式电机作为发电机，转子绕组通过一组背靠背变流器与电网相连，定子绕组也与电网直接相连。 定子、转子同时向电网馈电，都与电网存在功率交换，增加了控制难度。

根据绕线式异步电机的功率分配机制，定子功率、转子功率以及并网总功率之比为

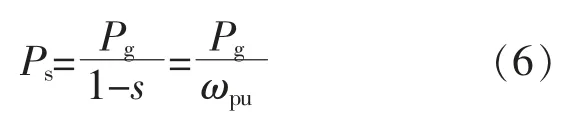
式中：Ps，Pg分别为 DFIG 型风机定子侧、转子侧输出功率；ωpu为风机转速的标幺值；s 为转差率，DFIG 的转差率一般处于±0.3 内。

DFIG 风机通过其内部的背靠背变流器，将工频电流变频为与转速相对应的交流励磁电流，为风机提供实现变速恒频功能的技术保障，其角度为

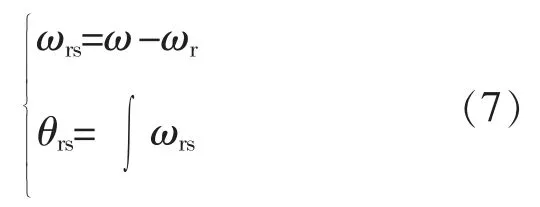
式中：ωr为风力发电机转子转速；ω 为定子旋转轴转速，通常控制中一般选取为电网额定电角速度，但在本文所提控制策略中选取为虚拟同步轴电角速度；ωrs为滑差角速度；θrs为滑差角，即交流励磁的相角。

DFIG 结构如图3 所示。

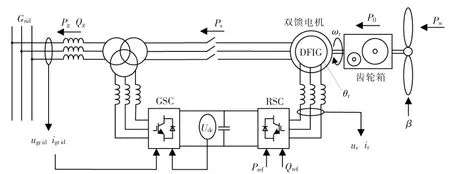
图3 DFIG 型风机结构图Fig.3 Structure of DFIG

图中，网侧变换器负责稳定直流侧电压，转子侧变换器负责依据给定参考量，调控发电机的输出功率。 由于DFIG 背靠背变换器的功率所占比重小，其直流侧电容的选取通常也较小，可开发势能不足。同时，直流侧电压的变化会加剧交流励磁系统设计的复杂程度。 故本文只针对转子侧变换器的控制进行改进，从风轮机转子中提取旋转势能用以增强系统的惯性。图中：θr为光码盘输出的DFIG 转子位置角；ugrid，igrid分别为并网点电压、电流；ur，ir分别为转子侧变流器出口电压、电流；Ps为定子功率；Pg，Qg为 DFIG 输出功率； Pref，Qref为发电机参考功率。

DFIG 模型在三相静止坐标系中是一个阶数高、变量多、耦合性强的非线性时变系统，为降低控制复杂性，实现对DFIG 输出端口功率的有效控制，须参考交流调速控制中的矢量控制技术，通过Park 变换将电流中的有功与无功分量解耦，再对两个分量电流进行单独调控。 当旋转坐标系转速ω′为任意转速时，根据DFIG 磁链方程和电压方程可得：

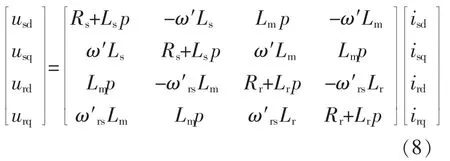
式中：ω′rs为任意旋转坐标下的转差角速度，ω′rs=ω′-ωr；p 为积分算子；usd，usq，isd，isq分别为定子电压电流在虚拟同步轴上的 d，q 轴分量；urd，urq，ird，irq分别为转子电压电流在虚拟同步轴上的d，q 轴分量；Rs，Rr分别为定、 转子电阻；Ls，Lr，Lm分别为DFIG 的定、转子电感、互感。

根据本文所提控制策略，将虚拟定子电压矢量U′s作为旋转坐标系的定向矢量，即d 轴，可得DFIG 电气量矢量关系图，如图4 所示。

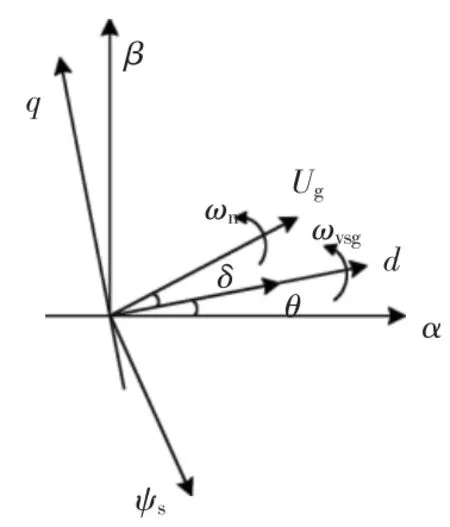
图4 基于虚拟定子电压定向的DFIG 型风机向量图Fig.4 Vector diagram of DFIG under the virtual stator voltage orientation coordinates

由图4 可知，由于定子电抗远大于定子电阻，定子电压 U′s和定子磁链 ψs的夹角近似 90°，ψs可看做与q 轴相重合，故定子磁链在d 轴的投影接近于0，在q 轴的投影近似于磁链的幅值。

根据磁链方程可得：

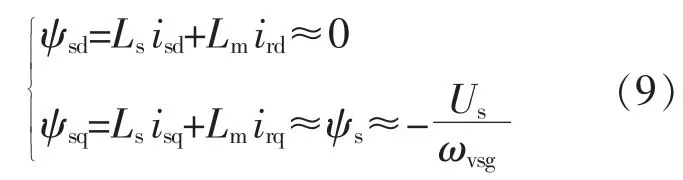
式中： ψsd，ψsq分别为定子磁链的 d，q 轴分量；Us为定子电压有效值；ψs为定子磁链的幅值；ωvsg为虚拟同步转速。

在正常工况下，ωvsg与系统电角速度均为100 π/rad，两者在相位关系上存在一个微小的相位差δ，即为VSG 控制所建立的虚拟功角。 当电网相位发生变化时，δ 随之变化，带动DFIG 型风机在并网点表现出与同步发电机调速器相类似的响应。

由式（9）可得：

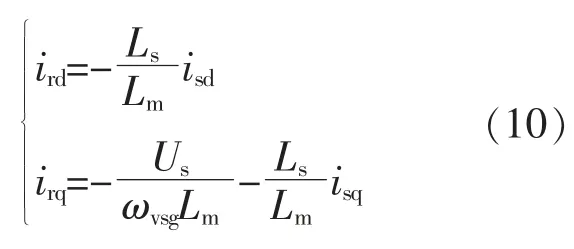
将式（10）带入式（8）可得：

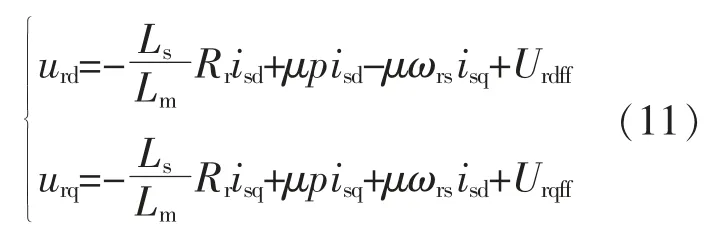
综上所述，依据式（1），（2），（6），（11）可构建出DFIG 型风机的虚拟同步控制框图，如图5 所示。其中，式（11）等式右侧的前两项作为定子电流的PI 控制项。

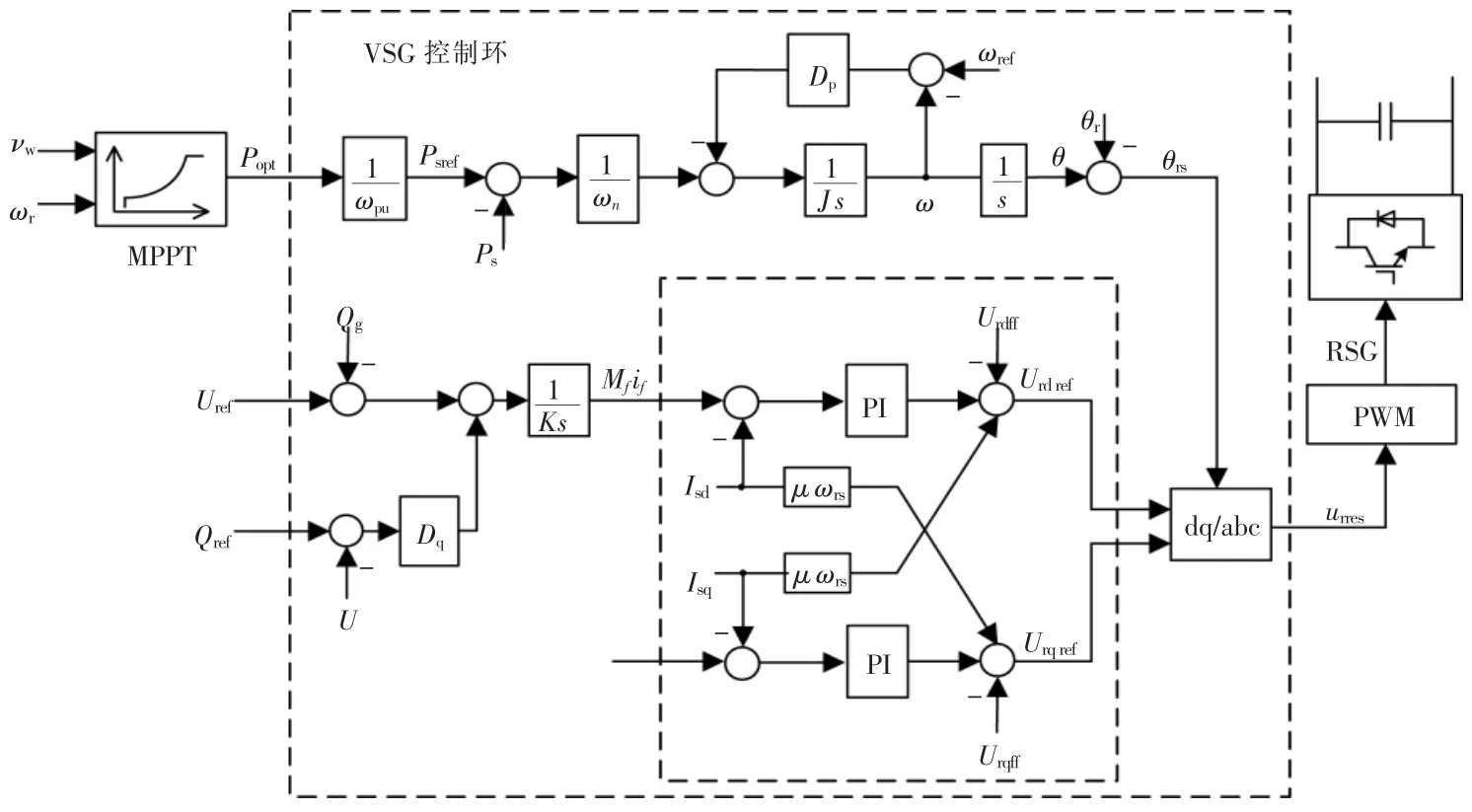
图5 DFIG 型风机VSG 控制框图Fig.5 Schematic of the proposed VSG control for DFIG-based WTs

图中：Popt为并网点风力发电机MPPT 输出功率；Psref为对应于当前转速风力机最大功率输出点的定子出口功率；Urdref，Urqref分别为在转速为 ωre旋转坐标系下转子变换器d，q 轴参考电压；Urdff，Urrqff分别为转子参考电压补偿分量的d，q 轴分量。

由图5 可知，本文所提出的控制策略可分为3 层：最外层为MPPT 控制层，用来满足稳态时风力机的风功率最大功率控制； 中间层为虚拟同步机控制环，由转子运动方程和虚拟励磁控制组成，负责对电网的扰动作出相应的响应； 最内层由电压和电流控制闭环组成，负责追踪虚拟同步机给出的参考值。

4 仿真分析

为验证所提控制策略对DFIG 机组的频率支撑能力，在PSCAD/EMTDC 中搭建了图3DFIG 单机并网模型。风力发电机选用额定容量为1.5 MW的DFIG 型风机，其详细参数如表1 所示。 电网短路比选为 2，对应电网短路阻抗为 0.5 pu。DFIG 型风机的两个背靠背变流器的模拟均采用PWM 平均值模型。为验证所提控制策略在稳态、电网功率变化和电压波动3 种情况下的响应情况，分别对风速扰动、频率扰动和电压扰动进行仿真分析。

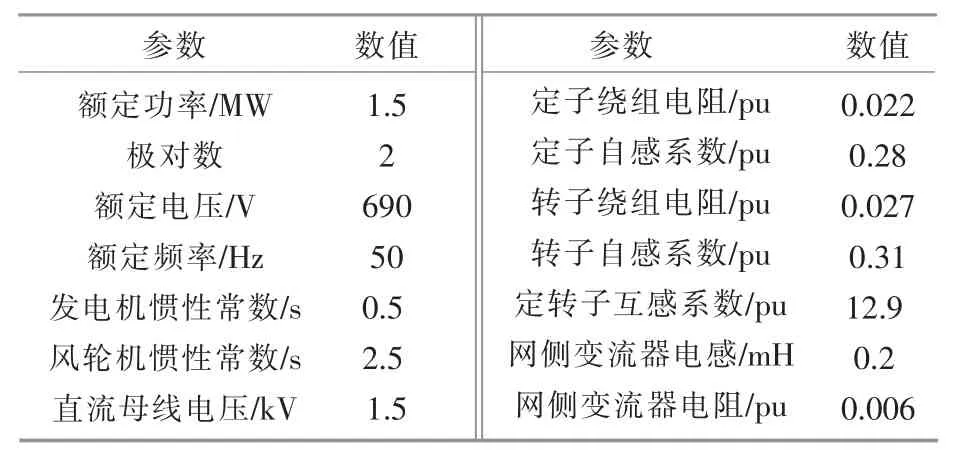
表1 DFIG 模型参数Table 1 DFIG wind turbine model parameters

4.1 风速变化

设定初始风速为7 m/s，假设电网运行稳定，频率恒定为50 Hz，此时风力机的最佳转速为0.788 pu。 VSG 控制中选取虚拟惯量常数 J 为15.19，时间常数 τf=J/Dp=0.01。 在 10～15 s 时引入风速扰动，风速为9 m/s，DFIG 风机功率与转速对阶跃风速的响应曲线如图6 所示。

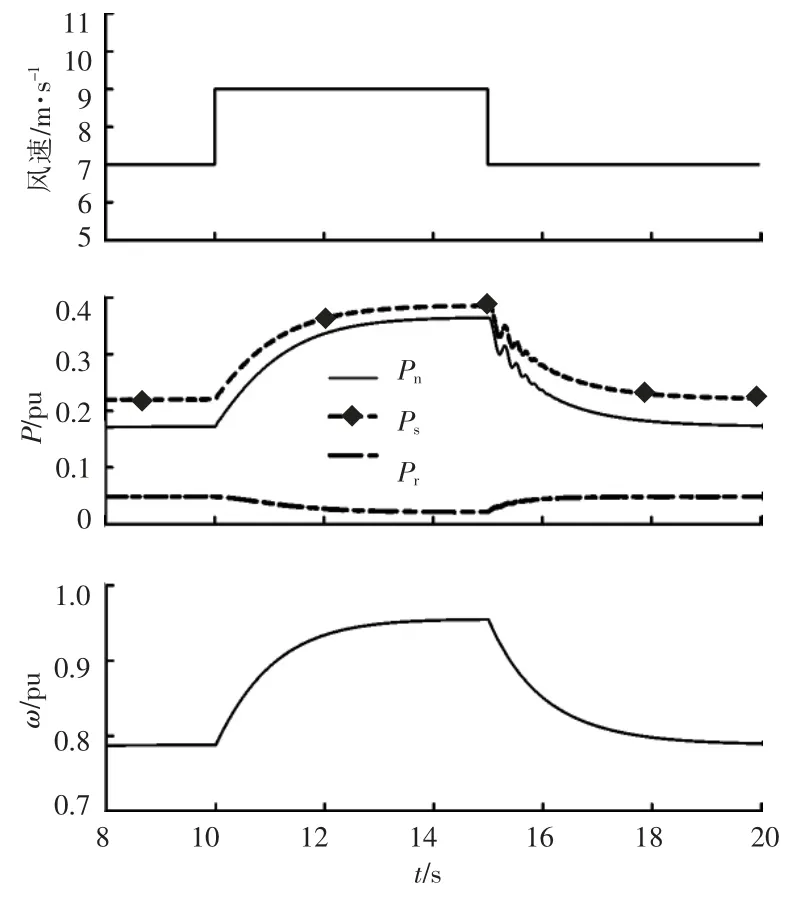
图6 风速变化时采用虚拟同步控制的仿真Fig.6 Simulation of DFIG-VSG control when wind speed changes

由图6 可知，当风速突然升高，对应风力机输出曲线开始突增。风机出口最大功率由0.17 pu 增至0.36 pu，转速由 0.788 pu 上升至 0.95 pu。 所提控制策略可使并网点功率快速追踪到最大功率曲线对应功率，当风速下降时也能较快的使功率回落，很好地满足了DFIG 稳态时工作于MPPT 运行方式的要求。

4.2 频率变化

假设系统频率在 10 s 由 50 Hz 降为 49.8 Hz，15 s 由 49.8 Hz 升至 50 Hz。 为了进一步研究虚拟同步控制参数对风功率输出的影响，在频率变化的基础上，对 J 依次取 8，13，15，18，取时间常数τf=0.01 并保持恒定，对 4 种情况进行仿真比较。仿真结果如图7 所示。

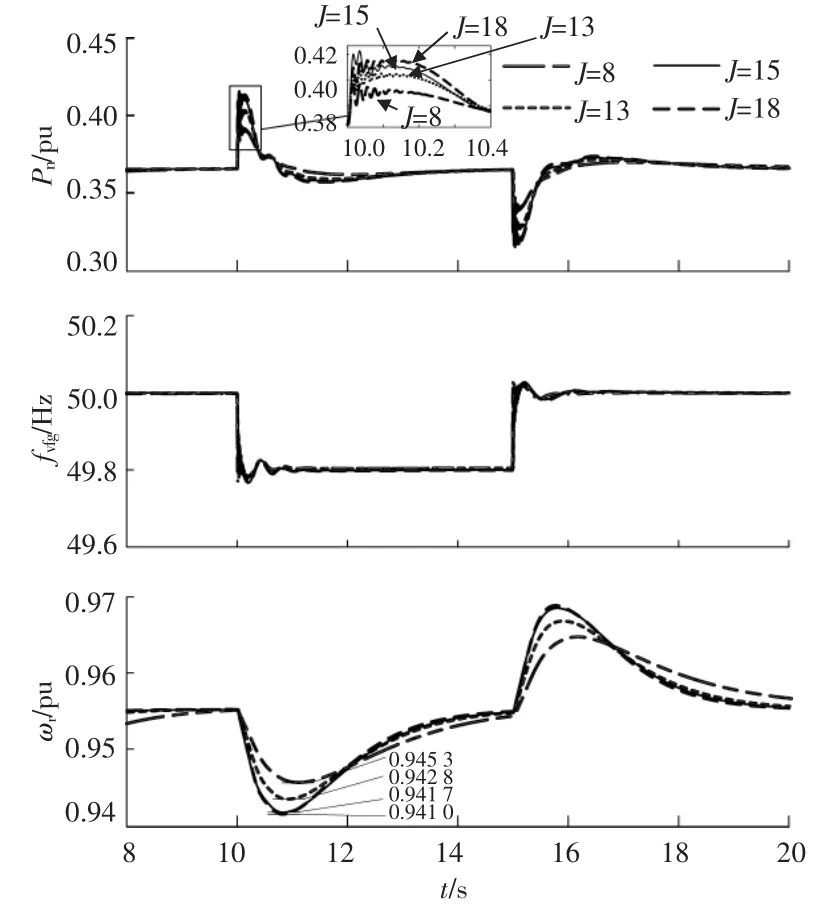
图7 系统频率变化时采用虚拟同步控制的仿真Fig.7 Simulation of DFIG-VSG control when system frequency changes

由图7 可知，DFIG 使用虚拟同步机控制后，系统频率发生突变时能够立刻做出响应。 以J=15为例，在10 s 时，系统频率突降，VSG 控制环的虚拟频率也随之下降，由于虚拟功角的突然增大，带动风轮机转速也开始下降，风机转速由稳态时的0.955 pu 下降至最低时的 0.942 pu。通过释放风轮机中的动能，风力发电机并网功率由0.36 pu 突升至 0.423 pu，并持续 0.1 s，在之后的 0.7 s 内功率逐渐回落至0.36 pu，虚拟频率也逐渐与电网频率同步速。 随后，风机逐渐缓慢地从电网吸收能量，使转速恢复至风速为9 m/s 时对应的最佳转速。由于能量吸收过程异常缓慢，整个暂态过程持续约4 s，比稳态时功率输出最低值仅下降了0.007 9 pu，相当于当前功率的2.13%，对电网带来的影响可忽略。 在15 s 时，系统频率由 48.8 Hz 恢复至50 Hz，整个响应过程与频率下降时相反，风轮机转速由0.955 pu 上升至0.97 pu，并网点功率下降至最低点达0.3 pu，整个暂态过程持续4 s。

对比可知，J 取值的不同决定了相同频率扰动下，风机响应速率与程度的差异；随着J 取值的增加，风电机组的频率响应程度逐渐增大，且为系统提供的有功支撑量与风轮机转速变化量呈负相关；当J 取值大于15 之后，有功响应程度几乎维持恒定；当选取的控制时间常数τf一定时，总响应持续时间十分相近，不同J 取值下虚拟频率fvsg的变化曲线也近乎重合。同时还可看出，虚拟同步频率fvsg在一定延时后，会重新自主追踪至电网的实际频率，若出现系统频率跌落持续时间较长的状况，也不会过度提取风轮机转子中的能量，避免了因转速降低过度而导致频率二次跌落，甚至整机脱网的可能性。

由仿真可得，当风速为9 m/s，系统频率降低0.4%时，单机容量为1.5 MW 的风电机组可为系统提供约94.5 kW 的有功支撑。

4.3 电压扰动

在10 s 时，令电网电压由稳态值跌落5%，在15 s 时恢复稳态，风机的无功功率响应曲线如图8 所示。

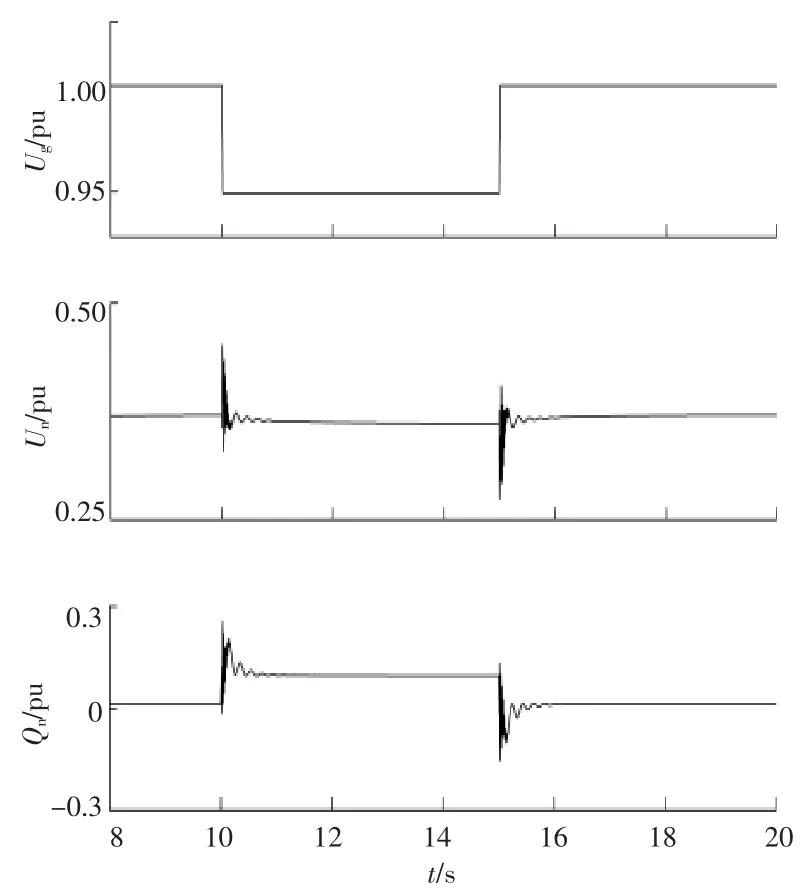
图8 系统电压扰动时采用虚拟同步控制的仿真Fig.8 Simulation of DFIG-VSG control when system voltage disturbance

由图8 可知，10 s 时电网电压 Ug由 1 pu 突降至0.95 pu，DFIG 型风机并网点的有功功率Pn与无功功率Qn都出现了约1 s 的振荡，但振荡结束后，有功功率基本维持与稳态时的输出，无功功率由0.008 pu 升高至0.09 pu，并维持稳定。 15 s时系统电压由0.95 pu 回升至稳态值，有功与无功功率也在1 s 后恢复稳态。 当电网电压波动时，风力发电机的无功控制环节迅速作出与同步电机励磁调节相类似的响应，通过对DFIG 控制的改进重新建立了无功功率与系统电压之间耦合关系。同时有功功率并未受其影响，很好地证明了所提控制策略可使DFIG 型风机的有功与无功分别独立控制，具有有功/无功相解耦的优势。

5 结束语

针对风电装机容量占电网比重的逐年上升给电网带来的隐患，提出一种基于虚拟定子电压定向的虚拟同步机控制DFIG 机组模型，经仿真验证，所提出三层控制结构可满足不同工况对风机的不同要求，在稳态时可使风机正常工作于MPPT 工作点，当电网发生频率波动和电压扰动时，均能像同步电机一样做出有效响应，从而为的大规模并网提供了可能。