基于Openfoam的怀来复杂地形风电场流动特性研究

叶昭良，闫 姝，史绍平，曾崇济，陈新明，张 波，马俊祥

（1.煤基清洁能源国家重点实验室（中国华能集团清洁能源技术研究院有限公司），北京 102209； 2.华能河南清洁能源分公司，河南 郑州 450000）

0 引言

复杂地形风电场的速度场流动特性的研究，对认识风电场场群的气动变化规律、优化风力机控制和机组排布策略、提高风电场风能利用效率具有重要的意义。 在风工程计算模型中，大气的边界层流动是充分发展的，流场上下游的参数具有较好的一致性。 然而使用该模型对复杂地形风电场进行数值模拟时，进出、口廓线分布未达到良好的一致性，给复杂地形的湍流强度评估带来了困难，影响到数值计算的结果评估[1]。

国内外许多学者对于复杂地形风电场的速度场流动特性进行了大量研究。 Richards P[2]提出了4 点大气边界层流动假设和入口边界条件，采用k-湍流模型较好地模拟了中性大气边界层。 在此基础上，Hargreaves D M[3]通过修改默认的粗糙度，实现了一定工况下的零流向梯度大气边界层数值模拟。 Yang Y[4]采用实验导出的随高度衰减的湍动能边界条件，速度场流动计算结果与实验数据有较好的一致性。 Parente A[5]采用上述类似的方法，通过添加湍动能和耗散率源项，结合基于粗糙长度的壁面函数，对均匀大气边界层和方体绕流的流动分离现象进行数值模拟，改进了大气边界层的流动模拟方法。 Balogh M[6]再次改进上述源项，在典型山丘地型和真实复杂地形中得到同样结论。几位学者从湍流模型参数、增加源项来提高大气边界层的自持性平衡属性，但仍存在入口边界条件设置问题。 Richards P J[7]除了考虑湍动能的平衡外，还考虑了压力梯度和剪切应力，结合实验结果进一步优化了大气边界层流动的计算。

部分文献采用了计算流体动力学（CFD）方法进行复杂地形下风电场尾流场特性的研究。 卢玉华[8]采用双方程k-模型方法，研究障碍物尺寸对下游山体流场的影响，得到障碍物尺寸距离山体8 倍或10 倍山高时，达到适宜风电场建设需求的湍流强度。 梁思超[9]简化山体流动问题为方体扰流流动，通过DES模拟方法对扰流机理进行了细致的研究，得到高雷诺数下马蹄涡系统的漩涡组成和发展机理。在此基础上，闫姝[10]采用Fluent 软件模拟了陡峭地形和风电机组前后的扰流现象，发现较大高宽比例诱导更大的山后流动分离，对场区选址有一定的影响。

综上所述，学者采用不同的研究方法对平坦地形和简化地形风电场下的的尾迹特性做了大量数值研究，但对于真实的复杂地形研究较少。本文提出一种基于Openfoam 的复杂地形模拟方法，并通过Askervein 山模型进行方法验证，确认了方法的有效性。 以怀来某复杂地形风电场作为研究对象，快速结构网格建模，得到了不同机位点的速度分布，分析了一定机位处的尾流分布。计算方法为风电场布机设计和控制策略的优化提供了数值参考，对机组稳定运行具有一定的参考意义。

1 几何模型与数值方法

1.1 几何模型

Askervein 山位于苏格兰一座岛屿上，高度仅为116 m。80 年代初，国际上多家单位合作完成了Askervein 山测风工作，分别进行了239°和210°速度进口的测量，测风速度充分，在国际上被广泛用于复杂地形模拟研究验证工作[11]。 本文以Askervein 山为研究对象[图1（a）]，进行 CFD 方法验证。 怀来风电场场内布置了 2 座雷达[图1（b）]，并选取T11，T12，T21 风机点位作为研究点（上述机位点距离雷达点位较近）。 图1（c）为一个月内怀来风场雷达387 在40～230 m 高程风廓线分布，怀来地形的主风向为西北西和东北东。

图1 验证地形和怀来复杂地形实地图及实际风场雷达风向图Fig.1 Verification terrain and actual complex terrain and wind direction rose figure at HuaiLai

1.2 数值方法

Askervein 山计算域的设置见文献[11]，地表粗糙度统一为0.03。 怀来地形的计算域如图2 所示。 怀来测风的主风向为西北西292.5°和东南东110 °，在 X 方向和 Y 反向分别设置为 21.5 km 和17.6 km，沿地表高度方向设置为10 km，地表粗糙度按照怀来实际地形粗糙度设置。

图2 怀来地形计算域Fig.2 HuaiLai terrian computational zone

网格划分采用自主研发的网格生成器绘制三维地形网格，先绘制背景网格，后进行局部加密。 壁面 y+＜30，满足湍流模型计算要求。 绘制三套怀来地形计算区域的网格，网格数分别为352万、814 万和1 452 万，风机点位附近分辨率分别为 30 m×30 m，20 m×20 m，10 m×10 m（图3）。从图3（b），（c）可知，地表分辨率逐渐加大，轮廓更为清晰，贴体网格捕捉更为明显。

图3 怀来地形网格Fig.3 Huailai terrain mesh

本文在进行网格无关性计算后，选用814 万网格。

边界条件：Askervein 山主风向为210°，测量时气流稳定，符合中性大气速度廓线分布，边界层厚度为500 m，对应位置风速为10 m/s，采用的摩擦速度为0.4 m/s。 在怀来复杂地形的计算中，按照一定扇区入口，以270°和292.5°风速方向为进口方向，入口设置速度分量，上表面壁边界为自由滑移壁面，下表面为无滑移壁面，出口压力设置为大气压力。入口边界条件廓线分布采用式（1）进行设置。 在Askervein 山验证算例中，采用WindSim（WS）类似的边界条件进行比较，见式（2）。

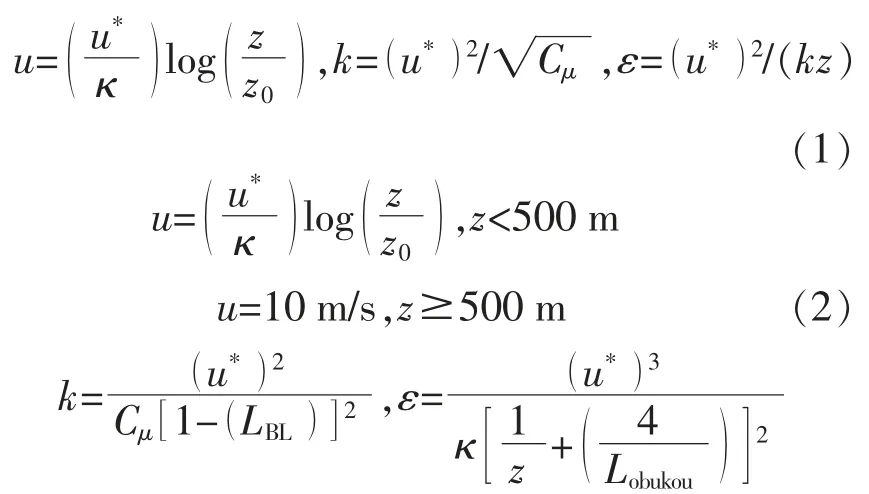
式中：u*为摩擦速度；κ 为冯卡曼参数，取为0.4；z为近地面高度；z0为壁面粗糙度，在导入的地形文件中包含着粗糙度信息，几何文件保留粗糙度信息，得到复杂地形下的不均匀特性；LBL，Lobukou分别设置为500 m 和1 000 m。

计算设置：数值计算采用基于Openfoam 开源CFD 工具，通过压力-速度耦合的SIMPLE 算法求解RANS 方程； 空间离散采用二阶精度的中心差分格式；湍流模型采用标准k-ε 模型，修正了湍流模型常数，适应复杂地形的计算要求。

2 结果与分析

本文首先以Askervein 山为研究对象，对研究方法进行验证； 然后以怀来某复杂风电场地形作为研究对象，经过网格无关性的验证后，研究了4组风向下的风场速度场和尾流特性分布。

2.1 结果验证

图4 为 Askervein 山在 AA-AA 和 B-B 山脊线的加速比分布图。 加速比为当地风速和入口风速的差值除以入口风速。 图中：B1，B2 分别为式（1），（2） 的入口边界条件；M1 和 M2 的网格地表分辨率分别为 133×133×35，200×200×35。 湍流模型参数设置包含 C0，C1 和 C2 3 种（表1）。

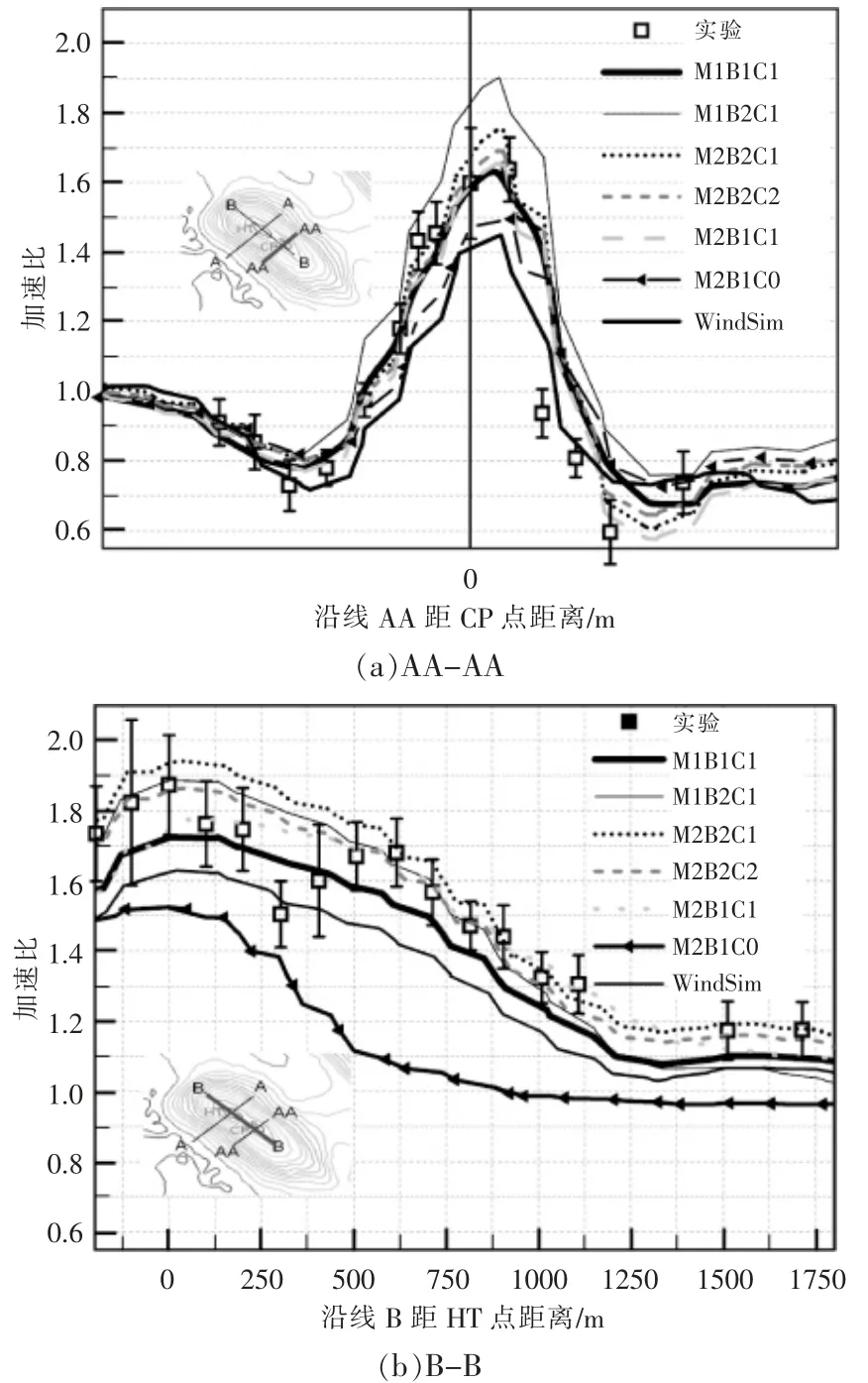
图4 沿着两个不同的山脊线AA 和B 的加速比分布Fig.4 The profile of speedup along the line AA and B

表1 湍流模型参数设置方案Table 1 Turbulent model parameter setup

WindSim 模拟结果表明，在不同的湍流模型参数和边界入流条件下，细网格的计算均较好地吻合试验参数。网格数验证后，计算了3 种入口配置方案，其中C0 为默认的k-ε 湍流模型参数设置，可知入口边界条件B1 和湍流模型参数C2 的配置参数模拟效果较好，因此，后续计算均采用B1 和C2 的配置方案。

验证Askervein 山的计算方案后，对怀来复杂地形的3 种网格配置方案进行验证。 图5 为3 套网格对比结果。 在上述工况下，不同网格差别较小，在轮毂高度处速度相差1%左右，均可以满足网格计算要求。出于计算效率和精度考虑，下面的模拟结果分析均基于841 万网格。

图5 三种网格数在两种扇区下T11，T12 机组的速度廓线分布Fig.5 The velocity profile at T11，T12 wind turbine under two velocity inflow conditions with three grid numbers

2.2 怀来地形不同扇区速度场分析

选取 841 万地形网格，采用 Openfoam 和Fluent 数值模拟方法，计算来流进口方向分别为正北、正东、正南、正西（顺时针方向）的数值模拟，对比云图和风机点位的风速轮廓线。 图6 为正北方向来流风电机组附近的流向截面速度云图。 通过速度边界层的对比分析可知，Openfoam 近地面的低速回流区域较多。

图6 正北方向来流在机组附近流向截面速度云图Fig.6 Velocity sectional contour nearby the wind turbines under the due north inflow

图7 为两台机组在2 个风机点位 T12，T21的速度廓线，其中T12 机组的海拔相对T21 较低，两台机组此时处于山体的下游尾迹区。 由图7可知，Openfoam 的速度廓线受到上游山体的分离流动影响，T12，T21 机位在轮毂高度处 （90 m）的速度相对于Fluent 分别相差了15%和12%，呈现一定的回流现象。

在正东主风向来流风况下，近地层风场受地形影响较为明显，与山体北侧来流汇集为向东运行（图8）。 由图8 可知：受地形影响，在小范围内形成背风测的涡旋型或辐散型流场，流动分离较为明显；该方向流动的大气边界层的自持性较差，流向速度梯度较大，流场需进一步的修正，以便得到更好的模拟结果；Fluent 得到的计算结果在山顶加速较明显，比Openfoam 计算结果偏高。

图7 正北方向来流在两台机组附近高度方向速度廓线分布Fig.7 Velocity profile nearby the wind turbines under the due north inflow

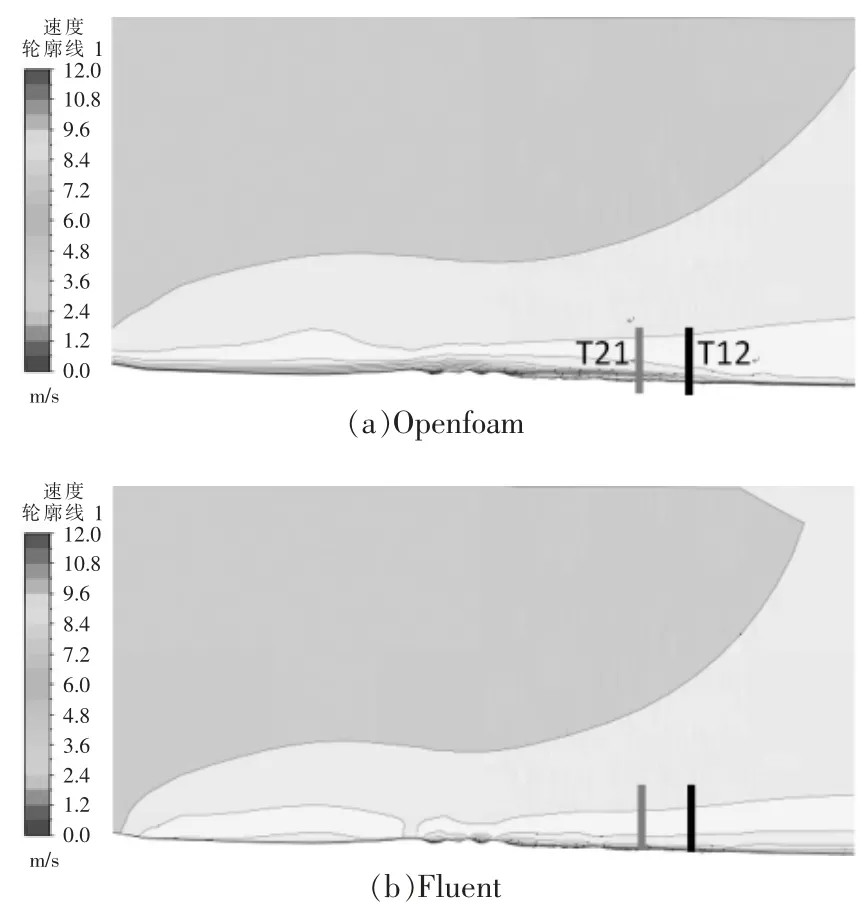
图8 正东方向来流在机组附近流向截面速度云图Fig.8 Velocity sectional contour nearby the wind turbines under due east inflow

图9 为两台机组的速度廓线分布，速度廓线均受到山体背风面流动分离的影响，在轮毂高度处速度与Fluent 分别相差20%和24%，出现一定的回流现象，风能品质下降。 正西和正南方向风电机组都处于山体前方，同平坦地形流场类似，自持性较好。

通过上述结果发现：采用Openfoam 和Fluent模拟方法能够比较合理地模拟出复杂地形上的近地层风场流动变化；受到局部不均匀粗糙度影响，Openfoam 边界层发展较厚。

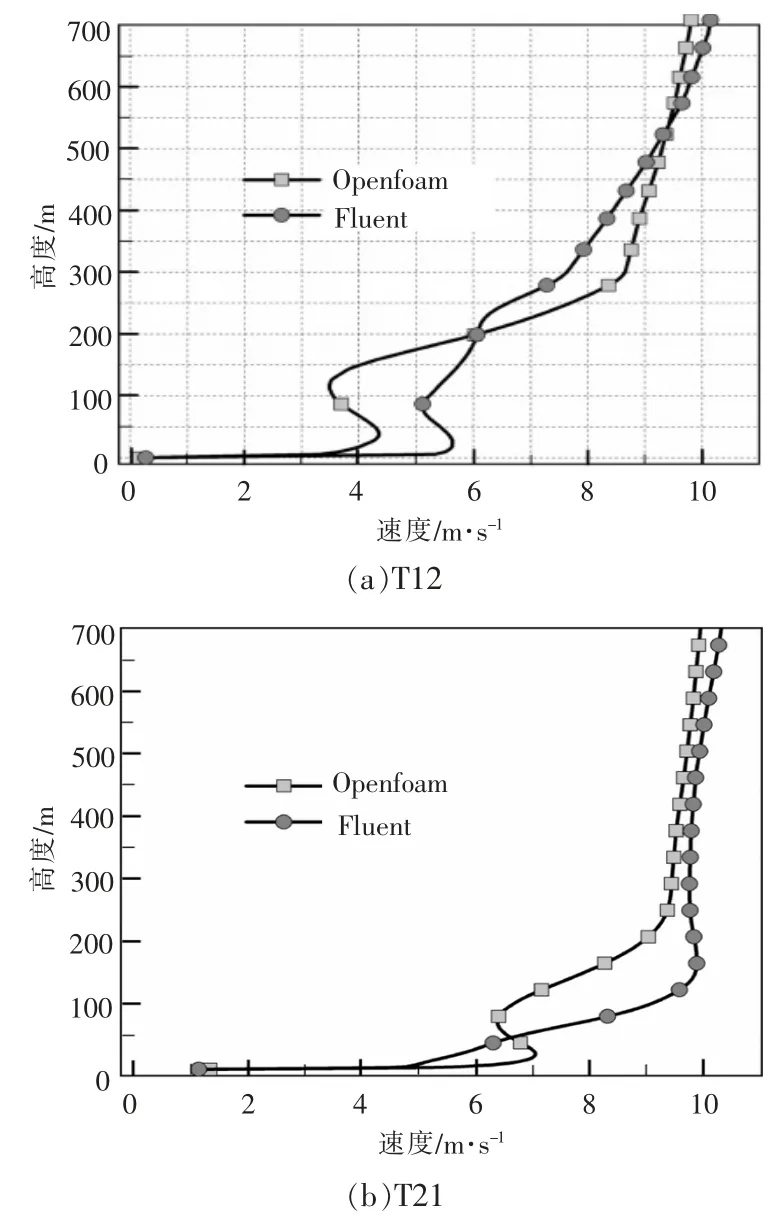
图9 正东方向来流在两台机组附近高度方向速度廓线分布Fig.9 Velocity profile nearby the wind turbines under due east inflow

3 结论

本文基于开源的Openfoam 数值软件进行了二次开发，采用自主研发的网格建模工具生成适应地形的帖体网格，通过Askervein 山的数值模拟验证了计算方法的有效性。 以怀来复杂地形风电场为研究对象，在考虑地形粗糙度的前提下，研究了4 组来流工况下的复杂地形数值模拟，分析了对应风向下的风速和尾流特性的关系，得到以下结论。

①复杂地形风电场的流场受到地形起伏影响较大，当风向经过山体后再经过风电场时，会使得风场整体风能品质下降，表现为流场的速度较低，尾流损失较大。

②不同扇区的入流计算表明： 在复杂地形影响下，流场绕流现象较为复杂，特别是低速流动时； 在轮毂高度处，各个机位点的速度与Fluent计算结果对比，相差15%左右，主要是受到山后回流的影响。入口边界条件修正、湍流模型参数修正等需要进一步完善。