“角”的自述
2020-04-14殷浩轩

嗨,大家好!我叫角。今天我来向大家做一个自我介绍。
我的出生是很神奇的:将一条射线绕着它的端点旋转,就产生了我。射线的端点是我的顶点,两条射线是我的边。我的边可以无限延伸哦!边的长短与我的大小无关,我的大小与射线旋转的程度有关。
为了让大家以后方便称呼我,下面我介绍一下我的名字:
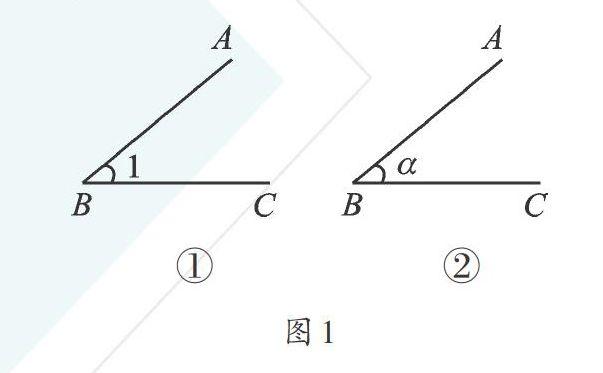
①你可以用三个大写的英文字母叫我,如ZABC(如图1-①),但要注意我的顶点字母要在中间哦;②在不引起混淆的情况下,大家也可以用表示我的顶点的一个大写字母称呼我,如∠B(如图1-①);③如果我不是复合的,大家也可以用数字表示我,如∠1(如图1-①);④我还可以用一个希腊字母表示,如∠а(如图1-②)。我的家族很大很大,下面我介绍一下我的家族成员:
根据我们的大小,我的家族成员可以分为五类:一是锐角,它们都小于90°;二是直角,它们等于90°;三是钝角,它们都大于90°且小于180°;四是平角,它们等于180°;五是周角,它们等于360°。
我们除了可以用度(°)表示以外,还可以用分(′)和秒(″)表示。它们之间的进率是60,即1°=60′,1′=60″。
大家可能要问我们的大小怎样来比较。我偷偷告诉你们,主要有两个方法:
(1)量角法:①对中——把量角器的中心与我的顶点重合;②合线——把量角器的零度线与我的一边重合;③读数——读出我的另一边所对的度数。
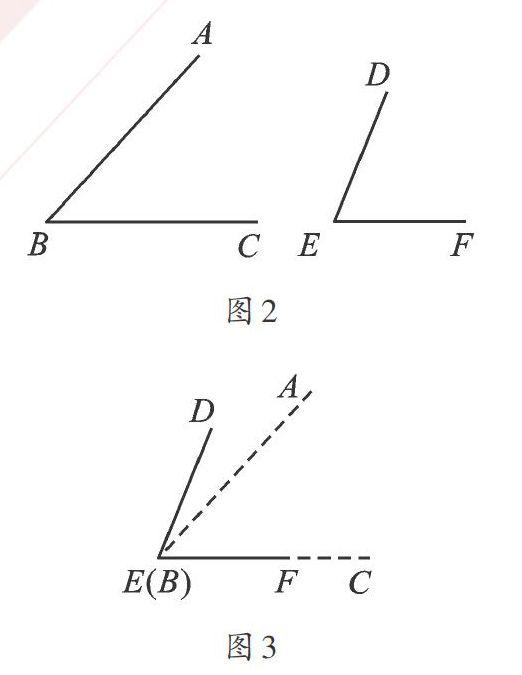
(2)叠合法:如比较∠ABC与∠DEF(如图2)。把∠ABC放在∠DEF上(如图3),使B和E重合,边EF和BC重合,DE和BA在EF的同侧。从图3可以看出AB在∠DEF内部,所以∠DEF>∠ABC。若AB与DE重合,则∠DEF=∠ABC。若AB在∠DEF外部,则∠DEF<∠ABC。
最后我再向大家介绍一下我的兄弟姐妹。我是∠1,若∠1+∠2=90°,∠1+∠3=180°,则∠2是我的姐妹余角,∠3是我的姐妹补角。如图4,∠4是我的兄弟对顶角:组成我们的两边在同一条直线上且方向相反。
通过我的自我介绍,相信同学们应该对我有所了解了吧。但我还有很多秘密没有告诉大家,希望大家以后要多多研究我,會有意想不到的收获哦!
教师点评
殷浩轩同学用拟人的手法从角的形成、定义、表示、大小比较等方面对角进行小结,语言生动活泼,相信同学们通过他的讲解,一定对角有了更深的认识。希望大家在今后的数学学习中经常运用类似的方法去研究几何图形,激发学习兴趣,提高知识应用能力和语言表达能力。
(指导教师:张杰)
