精雕细琢 精益求精

王国俊

在“平面图形的认识（一）”中，我们已經学习了平行和垂直这两种位置关系，会进行简单的推理。本章是“平面图形的认识（一）”的延续和提高。直线平行的条件和性质，图形的平移，三角形三边关系，多边形的内角和、外角和是初中几何的重要内容，有条理地表达和思考是规范证明的关键。在学习本章的过程中，希望同学们能注意以下几点。

一、提炼基本图形。提高解题效率

我们在进行有关几何图形的证明与计算时，往往会遇到形状类似、能得出某个固定结论、出现频率较高的图形。对于这些图形，我们要注意归纳、提炼，并能熟练运用。本章中与三角形内角和有关的基本图形有：

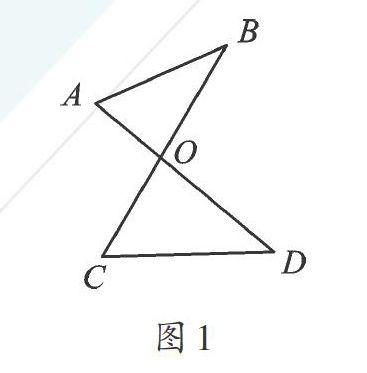
1.“8字”型。

如图1，线段AD、BC相交于点O，我们把类似图1的图形称为“8字”型。根据三角形的内角和是180°，且∠AOB=∠COD，不难得出∠A+∠B=∠C+∠D。

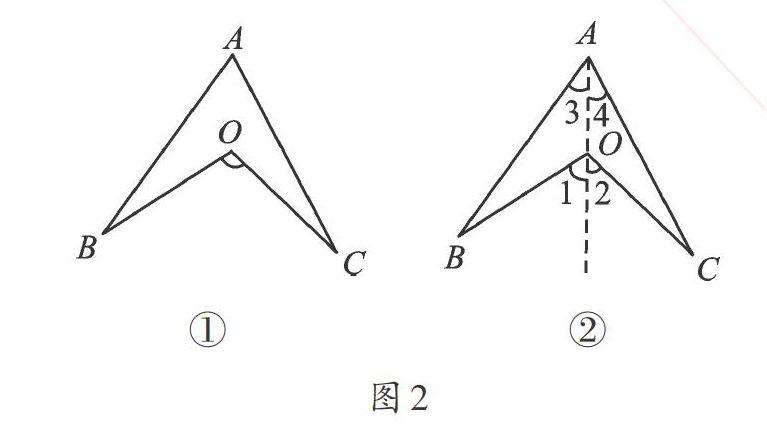
2.“飞镖”型。

如图2-①，我们把它称为“飞镖”型。通过作射线AO，如图2-②，可得∠1=∠3+∠B，∠2=∠4+∠C，所以∠1+∠2=∠3+∠B+∠4+∠C，即∠BOC=∠BAC+∠B+∠C。

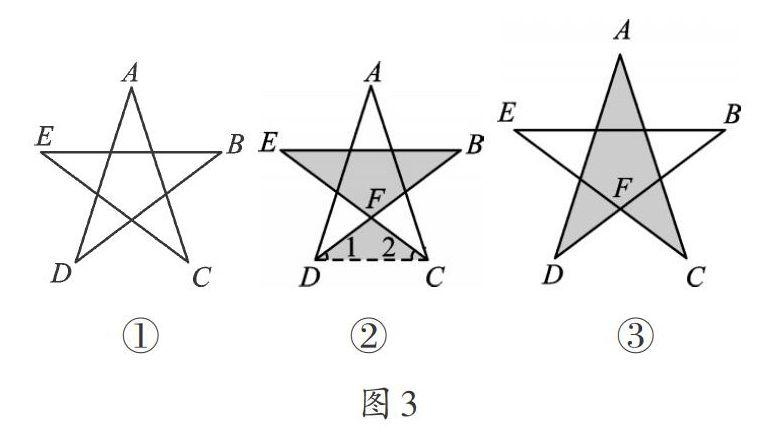
例1 图3-①是我们非常熟悉的五角星图案。你知道五角星的五个角的度数之和是多少吗？

【分析】本题的解题方法较多，我们可以借助上面的基本图形解决。连接CD，如图3-②，借助“8字”型基本图形，∠B+∠E=∠1+∠2，则五角星五个角的和就等于∠A+∠ADF+∠ACF+∠1+∠2，即转化成△ACD的内角和。

本题其实也可以借助“飞镖”型基本图形解决。如图3-③，则∠CFD=∠A+∠C+∠D。由∠CFD=∠BFE，可得∠BFE=∠A+∠C+∠D。那么五个角的和即为∠B+∠E+∠BFE，转化成了ABFE的内角和。

例2 如图4-①是一个六角星的图案，AD、BE相交于点O，其中∠BOD=75°，求∠A+∠B+∠C+∠D+∠E+∠F的度数。

【分析】本题看似复杂，但仔细观察，图4-①其实可以看成是由图4-②和图4-③两个“飞镖”型基本图形组合而成，则∠A+∠B+∠C+∠D+∠E+∠F=∠BOD+∠AOE。而∠BOD和∠AOE是一组对顶角，结合已知条件∠BOD=75°，则要求的六个角的和为75°+75°=150°，问题得以轻松解决。

本章虽然涉及的图形较多，但较多复杂的图形往往都是由一些基本图形组合而成的。因此提炼基本图形，把不同背景下的问题化归到同一模型中，则能化难为易，化繁为简，提高解题效率。

二、归纳解题策略。触类旁通

例3 如图5-①，直线AB∥直线CD，EFGHI为其中一条折线，求∠AEF+∠EFG+∠FGH+∠GHI+∠HIC的度数。

【分析】本题涉及的角较多，而条件只有一组平行线，结合平行线的性质，可以考虑过其中的点F、G、H分别作AB的平行线。如图5-②，将∠EFG、∠FGH、∠GHI分成∠EFF′、∠F′FG、∠FGG′、∠G′GH、∠GHH′、∠H′HI六个角。那么∠AEF+∠EFG+∠FGH+∠GHI+∠HIC可以看成是四组同旁内角的和。

平行线间的拐点问题，可以通过过拐点作平行线，转化成平行线间的角问题，利用平行线的性质解决。同学们在平时的学习过程中，要注重对一些解题技巧的归纳，通过解决一道题，学会解一类题。

三、注重一题多解训练，提高思维灵活性

例4 如图6-①，AB∥CD，AO与CO相交于点O。试猜想∠1、∠2、∠AOC之间的关系，并说明理由。

【分析】根据例3的解题方法，本题可以考虑过点O作AB的平行线，如图6-②，把∠AOC分成∠3和∠4，通过两组内错角解决三个角之间的关系;也可以考虑连接AC，得到一组同旁内角∠BAC、∠ACD，如图6-③，则（∠1+∠3）+（∠2+∠4）=180°，又∠3+∠4+∠AOC=180°，可得∠AOC=∠1+∠2;或者延长AO交DC于E，如图6-④，通过△COE的外角AAOC=∠2+∠3和一组内错角∠1=∠3，可得∠AOC=∠1+∠2。

同学们还可尝试过点O向右侧作AB的平行线，或延长CO与AB相交，亦可解决问题。

通过不同的解题方法体会平行的作用，可开拓思路，提高思维的灵活性，有利于创新意识的培养和数学能力的提升。因此，同学们在学习过程中切不可满足于掌握一种解题方法，应尝试多种方法，学会比较各方法的优劣，提升数学思维的敏捷性。

四、掌握数学思想，提升数学素养

本章内容涉及较多的数学思想方法，同学们需认真体会，内化于心。

如探究直线平行的条件时，通过角度（数）的变化观察两直线位置关系（形）的变化，这是数与形的结合;在探究多边形的内角和的过程中，我们尝试了不同的方法，如在多边形内取一点，或在多边形的边上取一点，或过其中的一个顶点分别连接其他顶点（如图7），把多边形的内角和问题转化成若干三角形的内角和的问题，这是化未知为已知。

在解决问题的过程中，当已知条件不确定时，我们还需要分类讨论。如当一个角的两边平行于另一个角的两边时，这两个角的关系是相等或互补。又如一个正方形剪去一个角后，求剩余部分的多边形的内角和，剩余部分既可能是三角形，也可能是四边形或五边形（如图8）。再如平面内有六条直线，其中任何三条直线都不共点，要求画出图形说明交点的个数问题，可以从平行线的角度考虑，先考虑六条直线都平行，再考虑五条、四条、三条、两条直线平行，最后考虑都不平行的情况。从特殊到一般，这是解决问题的常用方法，其中也渗透了分类讨论的思想。此外，同学们还要注意归纳。

数学思想方法是数学最本质、最具价值的内容，是数学知识的“灵魂”。因此，同学们在学习数学的过程中，既要掌握数学知识，又要重视数学思想方法的学习，从而有效地提升自身的数学素养。

本章既是规范证明的开端，也体现出数学思维能力的一个飞跃。在学习本章的过程中，我们不能忽视基础知识的学习，要抓住重点，精雕细琢，注重数学思维能力的提升;要注重归纳，精益求精，灵活运用所学知识解决问题。