有趣的“钟面角”问题

郭金网

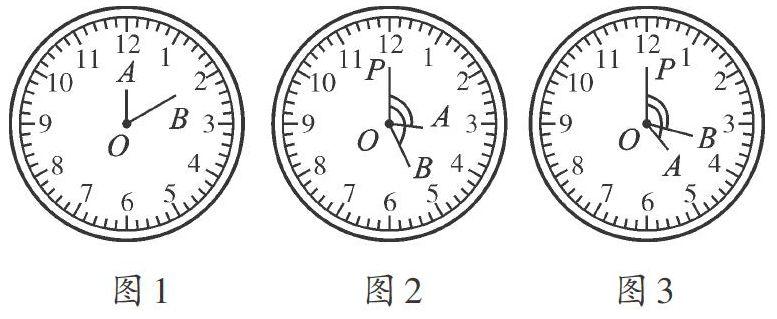
时钟在我们的生活中处处可见。随着时间的变化，时钟上的时针与分针会形成一个个角，我们把这样的角称为钟面角（通常指0°～180°的角）。如图1，∠AOB为钟面角。钟面角的计算是同学们经常遇到的一类有趣的问题。下面从一道实际问题出发，探究、归纳出钟面角的计算公式。

我们知道，钟面数字从1到12共有12大格、60小格。1周角等于360°，所以钟面上每个大格对应30°的角，每个小格对应6°的角。这样，时针每走1小时对应30°的角，每走1分钟对应30°÷60=0.5°的角;分针每走1分钟对应6°的角。

例题 求3点25分时针与分针的夹角。

【分析】如图2，假设分针OB、时针OA都是由OP（指针指向12）顺时针旋转得到，则此时时针与分针的夹角∠AOB=∠BOP-∠AOP。接下来，应分别求出分针旋转的角度（∠BOP）和时针旋转的角度（∠AOP）。

分针每分钟转6°，转了25分钟，也就是转了6°×25=150°，所以∠BOP=150°;时针每小时转30°，每分钟转0.5°，现在转了3小时25分钟，所以转了（30°×3+0.5°×25）=102.5°，所以∠AOP=102.5°。所以∠AOB=∠BOP-∠AOP=150°-102.5°=47.5°。

【推广】我们可以推广到一股情況，求m时n分时针与分针的夹角α（0°≤α≤180°）。

当时针OA与分针OB位于OP所在直线的右侧时：

如果分针OB在时针OA的前面（“前面”是指从顺时针方向看，OB在OA之前），女口图2，∠AOB=∠BOP-∠AOP=6°n-（30°×m+0.5°×n）=5.5°n-30°m：

如果时针OA在分针OB的前面（同样从顺时针方向看），如图3，∠AOB=∠AOP-∠BOP=（30°×m+0.5°×n）-6°n=30°m-5.5°n。

由此可得，钟面角“的度数=|5.5°×分-30°×时|。

同理：当时针OA与分针OB位于OP所在直线的左侧时，仍然可得钟面角α的度数=|5.5°×分-30°×时|。

当时针OA与分针OB位于OP所在直线的异侧时，由于0°≤α≤180°，钟面角α的度数=360°-|5.5°×分-30°×时|。

后两种情况，同学们可以试着自己推导一下。