传染病动力学模型及其在新型冠状病毒肺炎疫情仿真预测中的应用综述

李 昊，段德光，陶学强，陈 恩，高树田

（军事科学院系统工程研究院卫勤保障技术研究所，天津300161）

0 引言

传染病防控能力建设事关人民生命健康与国家社会稳定。面对日益严峻的传染病防控形势，传染病动力学模型在传染病疫情发展趋势预测、科学防控指导与评估中持续发挥着重要作用，为公共卫生管理者的决策与高效干预措施的实施提供了重要数据依据和理论支撑[1]。

本文首先梳理具有代表性的传染病动力学模型，然后结合新型冠状病毒肺炎（COVID-19，以下简称“新冠肺炎”）疫情发展现状，探讨国内外研究者开展的基于传染病动力学模型的新冠肺炎疫情仿真预测研究成果，最后提出对未来发展的一些思考建议。

1 传染病动力学模型研究进展

传染病动力学模型通过假设、参数、变量以及它们之间的联系定量揭示传染病主要特征，依托疫情暴发早期数据，纳入未来不确定性，帮助发现传染病传播机理，科学预测疫情流行趋势。传染病动力学模型根据数学表现形式可分为两大类：决定论模型和网络动力学模型。目前，以一般增长模型和室模型等为代表的决定论模型仍占据重要学术地位，但是随着人工智能与计算机技术的发展，以元胞自动机和人工神经网络等为代表的网络动力学模型也逐渐被关注并应用。

1.1 决定论模型

决定论模型的基本假设是目标区域种群总数为常数或渐近常数，模型表达形式以微分方程为主，根据建模依据还可以将决定论模型细分为现象学模型和机理学模型。现象学模型主要依托经验观察结果，强调模型研究对象对经验观察结果的可重现性；而机理学模型则考虑疫情传播动力学机理，基于一系列微分方程实现影响疾病传播过程的参数定量化，进而阐释目标人群中流行病学状态的发展过程[2]。

1.1.1 现象学模型

（1）GGM（generalized-growth model）模型。GGM模型已被证明适用于描述和预测传染病早期增长模式[3-4]，其微分方程如下：

其中，C'（t）为新增确诊病例数，C（t）为累计确诊病例数，r 为无干预条件下的自然增长率，p 为增长减速因子。

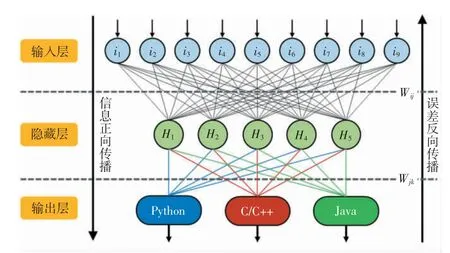
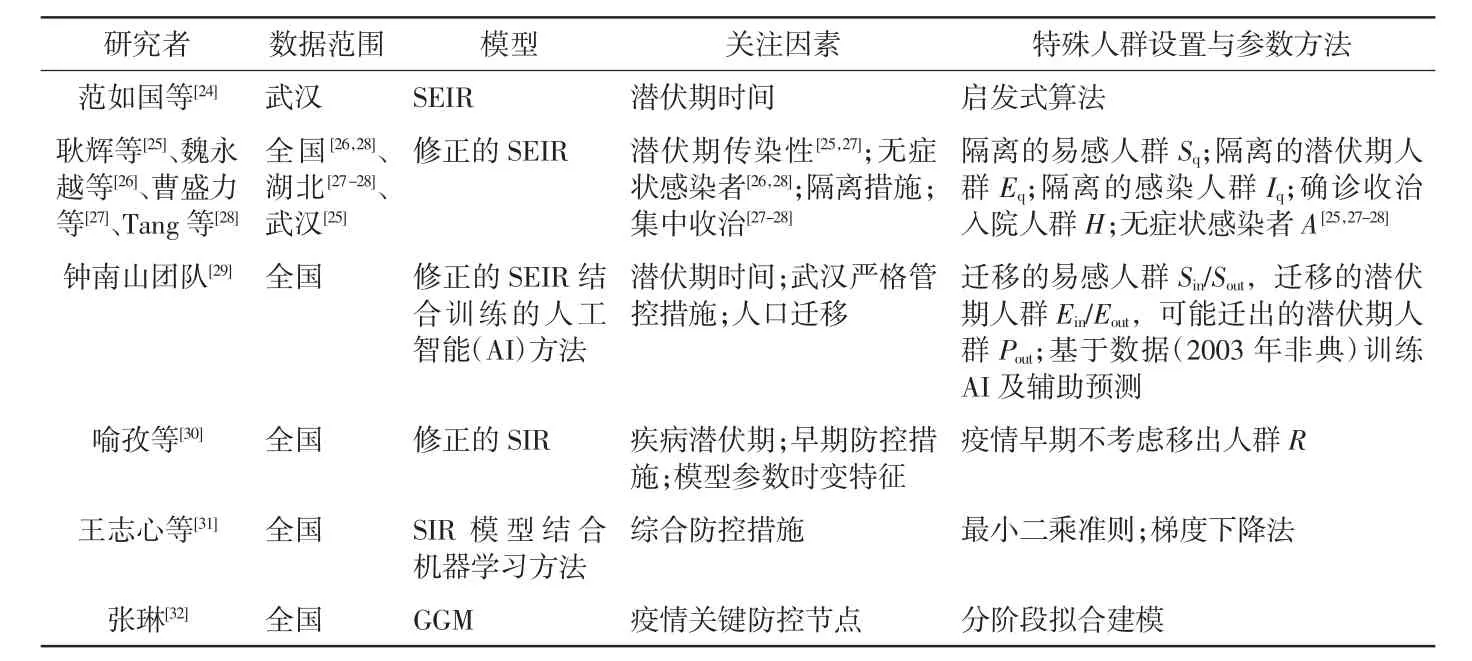
累计确诊病例函数C（t）在p=0 时，呈线性增长；在p=1 时，呈指数增长；在0

（2）GRM（generalized Richards model）模型。GRM模型是对原始Richards 增长模型[5]的扩展优化，可模拟实现疫情暴发早期常见的亚指数增长模式，同时也具备较好的疫情峰后发展预测能力[6-7]。其微分方程表达如下：

其中，C'为新增确诊病例数，C 为累计确诊病例数。模型中包含4 个自由参数：无干预条件下的自然增长率r、增长减速因子p、模型与经典S 型增长曲线偏差的衡量参数a 及种群总体数量K。

1.1.2 机理学模型

（1）SIR（susceptible-infected-recovered）模型。Kermack 等[8]于1927年首次提出SIR 模型（如图1所示），假定目标地区人群数为常数且康复后不再被传染，将目标人群划分为易感人群（S）、感染人群（I）、恢复人群（R）3 类，构建如下SIR 模型及微分方程：

其中，以天为基本时间单位时，λ 为日接触率，β 为日传染率，γ 为日治愈率，进而估测传染病的基本再生数R0（R0=β/γ）以及更有指导意义的有效再生数Rt[Rt=R0×S（t）/N（N 为目标人群总数）]。

图2 SEIR 模型[9]

（2）SEIR（susceptible-exposed-infected-removed）模型。SEIR 模型[9]（如图2 所示）是目前最具代表性的固定人群传染病动力学研究数学模型。该模型考虑了传染病潜伏期特征，在SIR 模型基础上增设潜伏期人群（E），构建如下SEIR 模型及微分方程：

其中，以天为基本时间单位时，λ 为日接触率，β 为日传染率，σ 为致病率，γ 为移出率（包含康复与死亡）。

基于上述4 个定量参数，可以估测传染病的基本再生数R0、有效再生数Rt，持续跟踪每日新增确诊病例C'（t）[C'（t）=σE（t）]与累计确诊病例C（t）[C（t）=I（t）+R（t）]的变化趋势。

1.2 网络动力学模型

网络动力学模型主要研究动力学模型在不同网络上的性质以及与相应网络静态统计性质的联系，具有结构与规则固定的特征。目前，在传染病理论研究中应用较广、具有代表性的网络动力学模型研究方法包括元胞自动机（cellular automata，CA）、人工神经网络（artificial neural network，ANN）等。

1.2.1 元胞自动机模型

元胞自动机模型是由一系列模型构造的规则构成，不依靠严格定义的物理方程或函数来确定，在时间、空间、状态上都离散，且空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力[10-11]。元胞自动机的概念于20 世纪40年代由冯·诺依曼提出，在20 世纪80年代开展了全面的研究与分类[12]，自20 世纪90年代中期开始被广泛应用于传染病传播过程的描述与研究。

元胞自动机属于一个方法框架，可视为由一个元胞空间和定义于该空间的变换函数组成，具体可用一个四元组形式[13]表示：

其中，CA 代表一个元胞自动机系统；Ld代表一个任意正整数维（通常为一维或二维）的规则网格空间，包含若干网格单元（即元胞，cell）；S 代表一个离散的有限集合，用来表示各个元胞的状态；N 代表含中心元胞的邻居集合；f 为状态转换函数或局部规则，即根据t 时刻某个元胞（中心元胞）的所有邻居的状态组合来确定t+1 时刻该元胞的状态值。

1.2.2 人工神经网络模型

人工神经网络模型是一类仿生型网络动力学模型，具有自组织、自适应及自学习功能，其依据生物体神经系统的工作原理，将诸多节点人工神经元（基本单元）以一定的规则或方式连接形成网络，模拟展现系统的整体性行为[14-15]。误差反向传播（back propagation，BP）神经网络模型（如图3 所示）是人工神经网络中应用最广泛的一种模型。

图3 BP 神经网络模型

基于以BP 神经网络为代表的人工神经网络构建传染病数学模型可以依托网络连接权系数实现高度并行分布式处理，具备联想记忆、自组织、自学习能力，通过训练学习可以逼近任意非线性映射，对传染病流行趋势具有较高的预测精度[16-17]。

2 传染病动力学模型在新冠肺炎疫情仿真预测中的应用

2.1 国内新冠肺炎疫情简述

本次新冠肺炎疫情由新型冠状病毒（SARSCoV-2）引起，世界卫生组织预测新型冠状病毒基本再生数R0为1.4～2.5，具有潜伏期（平均3～7 d），且潜伏期也存在传染性；人群普遍易感，并可持续人传人；病毒主要依靠飞沫传播和接触传播，存在气溶胶传播（限于相对封闭环境内长时间暴露于高浓度气溶胶条件下）与粪-口传播可能性，多数感染可导致新冠肺炎，存在无症状感染者且具有一定传染性[18-19]。

由于暴发突然，加之春运期间人口迁移规模庞大[20-21]，本次新冠肺炎疫情的蔓延速度和防控难度前所未有。截至2020年3月5 日24 时，31 个省（自治区、直辖市）和新疆生产建设兵团报告累计确诊病例80 552 例，累计死亡病例3 042 例，累计治愈病例53 726 例[22-23]。武汉“封城”（1月23 日）以来的疫情发展情况如图4 所示。

2.2 传染病动力学模型在新冠肺炎疫情仿真预测中的应用

本次新冠肺炎疫情存在潜伏期与无症状感染者，因此，绝大多数研究者基于经典的决定论模型（如SEIR 模型[24-29]、SIR 模型[30-31]、GGM 模型[32]等）开展疫情仿真与发展预测，基于训练的人工智能（AI）[29]或机器学习[31]方法也有一定的辅助应用。具有代表性的研究模型及特点汇总见表1。

SEIR 模型特别考虑了传染病存在潜伏期的情况，因此在本次新冠肺炎疫情仿真预测中的应用最为普遍。其中，范如国等[24]模拟不同潜伏期（5、7、10 d）对应的武汉峰值确诊病例（29 000、31 500、34 100例），并预测武汉疫情拐点将出现在2月20 日至25 日。耿辉等[25]估算病毒基本再生数R0≈2.4～2.7，通过仿真发现基于严格限制出行的隔离措施可使潜伏期和感染人群的峰值降低45.71%和29.90%，预测武汉最晚于3月初出现疫情拐点。魏永越等[26]基于SEIR+CAQ模型验证了每日新增确诊病例变化曲线已在2月初达到峰值，并较准确地预测了2月底全国的累计确诊病例数（预测80 417 例，官方2月29 日数据为79 824 例[22]）。曹盛力等[27]开展湖北省疫情的回溯研究，评估并验证了防控隔离和医学追踪隔离对疫情大面积扩散的有效遏制作用，以及集中收治对感染人数峰值迅速回落的关键影响。Tang 等[28]通过仿真发现密切接触者追踪隔离可有效降低病毒有效再生数Rt和传播风险，武汉及时采取“封城”举措可有效降低北京随后1 周内确诊病例数（较未采取封城举措，降幅可达91.14%），并比较准确地预测了国内每日新增确诊人数达到峰值的时间（预测2月5 日前，实际2月4 日）。钟南山团队[29]科学考虑了武汉“封城”前后的人口迁移情况，通过干预措施评估发现，如果武汉“封城”管控措施推迟5 d 实施，国内疫情规模将扩大至3 倍；降低武汉管控力度，很可能导致湖北省3月中旬出现二次疫情高峰。该团队还创新结合训练的AI 方法（基于2003年SARS 数据）辅助预测疫情流行趋势，做出了基本符合疫情实际发展趋势的权威预测：国内疫情将于2月下旬达到高峰，截至4月底国内疫情现存确诊病例将不高于70 000 例，湖北省不高于52 000 例，广东省和浙江省不高于1 200 例[29]。

此外，喻孜等[30]考虑了病毒潜伏期及早期诊断周期带来的时间延迟效应，拟合获得具有时变特性的参数变化方程，解读了疫情早期重要防控手段实施的影响效果，预测了国内现存确诊病例数峰值（预测54 000 例，官方公布58 016 例[22]）及出现时间（预测2月9 日左右，官方公布为2月17 日[22]）。王志心等[31]估计疫情在2月13 日左右出现拐点，结合SIR 模型与机器学习的方法，评估国内重要省市疫情严重程度，并预测疫情最终确诊病例在75 000 例左右。张琳[32]基于GGM 模型，分无障碍指数增长、次指数增长及次线性增长3 个阶段做出与疫情实际数据吻合度较高的模型拟合，在揭示新冠肺炎疫情传播机理及发展趋势预测方面开展了有益探索。

图4 新冠肺炎疫情数据变化曲线

表1 应用于新冠肺炎疫情预测的代表性传染病动力学模型及特点

综上所述，决定论模型在应用中往往能给出与实际统计结果符合度较好的结果，在本次新冠肺炎疫情发展预测中也被广泛应用并发挥了较好的数据理论支撑与科学防控指导作用；网络动力学模型从研究方法和适用对象上更加适合传染病传播趋势模拟的复杂性要求，通过对以往疫情数据或目前有限数据的学习，也发挥了疫情发展辅助预测与验证作用。

3 模型局限性与未来发展启示

传染病传播过程中自然因素和人为因素的相互交织大大增加了建模仿真预测的复杂性，必须要在全面了解疾病传播特征与重要影响因素的基础上，提出合理假设，构建科学的数学模型与验证方法，充分挖掘疫情发展数据的内在规律，有效控制模型参数的可识别性、适度敏感性，才能做出科学合理的疫情发展预测，有效指导疫情防控与救治工作。

3.1 传染病动力学模型应用的局限性

传染病动力学模型在本次新冠肺炎疫情的仿真预测应用中仍然存在一定局限性：

（1）新冠肺炎疫情暴发期间正值春运，人口迁移因素不可忽视，导致以省（市）为研究对象的决定论模型中种群总数为常数或渐近常数的基本假设缺乏合理性。

（2）新冠肺炎疫情的综合防控措施相辅相成，现有的传染病动力学模型研究难以纳入疫情发展与防控中所有重要的影响因素，仿真预测结果结论或多或少存在片面性。

（3）决定论模型的参数敏感性较强，而本次以武汉为辐射中心的新冠肺炎在全国各省市的传播存在一定的空间异质性与时间迟滞性，采用统一模型与参数设定的全国疫情发展预测结果科学性有待验证。

（4）鉴于暴发初期疫情数据的有限性与不完整性以及以往疫情数据的差异性，基于数据学习的网络动力学模型单独应用并开展科学预测仍然存在不少限制。

3.2 未来发展启示

（1）加强传染病的快速认知与防控能力。及时了解传播机理，科学部署防控干预措施，为准确构建传染病动力学模型提供理论支撑和政策指导。

（2）构建全面的疫情信息实时共享平台。明确统计规则，严格上报时限，为模型拟合与参数估算提供精确完整的数据支撑。

（3）推进多传染病动力学研究的多模型结合应用。充分利用经典决定论模型与新兴网络动力学模型优势，提升模型的自适应性与仿真预测科学合理性。

4 结语

传染病动力学模型在传染病传播与发展的理论性研究与科学防控指导方面发挥着重要作用。未来传染病动力学模型的研究需要满足传染病传播与防控过程的复杂性要求，需要在加强传染病的快速认知与防控、推进疫情信息实时共享、探索多模型结合应用的基础上，充分利用计算机科学与智能化前沿技术发展成果，持续为公共卫生决策与政策制定者提供理论支撑与数据支持。