船闸人字闸门底枢摩擦副接触应力分析

周紫嫣

船闸人字闸门底枢摩擦副接触应力分析

周紫嫣

（三峡大学 机械与动力学院，湖北 宜昌 443000）

底枢是人字闸门的重要的支承运转部件，其磨损将造成人字闸门失效，影响船闸功能。对闸门底枢摩擦副进行受力分析，对其受闸门自重和外载荷时的接触应力计算公式进行推导，再利用ANSYS软件对闸门底枢蘑菇头受自重和外荷载时的接触应力分布进行有限元分析，将将理论计算结果和有限元结果进行比较，二者误差较小，证明了理论公式的合理性。该公式结果表明：最大接触应力出现在外载荷的垂直接触点；最大接触应力与各点的接触应力随着外载荷的增大而增大，且呈正比关系；接触应力分布关于外载荷倾角有对称分布部分，最大接触应力随着外载荷倾角的增大而增大；闸门底枢半径增大，接触应力减少。

人字闸门底枢；接触应力；理论公式

闸门运转件特别是水下运转件的磨损问题是影响船闸运行的重要原因。底枢是人字闸门的重要运转件，由于运行时所受工况复杂、载荷不对称等影响，容易导致失效。为了延长人字闸门底枢的寿命，从20世纪90年代开始已有针对性的研究[1]，主要集中在选材、构件加工工艺及润滑体系等几方面。司敬阳[2]提出一种全新结构的底枢，在蘑菇头骨架上镶嵌一层可拆卸的高分子工程合金材料MGB，将传统的铜衬套改用坚固耐用、耐腐蚀的不锈钢材料；李玲君[3]在结构上将支承座与枕垫块支承的部位设计成分体式，设置蘑菇头球头弧度大于180°等改善底枢性能，同时设置循环加油装置、有双向密封圈优化底枢的润滑系统、改善底枢的运行条件；郭文涛[4]通过销/盘配副面接触摩擦的形式进行模拟试验，对闸门底枢摩擦副QT600-3/40Cr在脂润滑条件下进行磨损试验研究，获得不同接触应力作用下的摩擦学性能。

由于人字闸门底枢摩擦副低速重载的特性，接触区容易出现润滑失效[5]，从而严重影响底枢寿命，造成因底枢运转件磨损严重而被迫断航抢修或提前大修的情况[6-8]。因此对人字闸门底枢摩擦副的接触应力的研究尤为重要。诸多学者采用软件仿真对其进行分析。岳陆游等[9]用有限元软件对两接触零件的位移、应力和应变等参数进行计算，并对参数选择和结构设计进行了优化分析，结果表明，各参数优化计算中蘑菇头、帽皆处于弹性变形状态，且在有限元数值计算下外载作用面积、摩擦因数、球面半径和配合间隙等对接触变形的影响与赫兹公式理论分析结果一致；殷恋飞[10]应用有限元软件对参数选择和结构设计进行了优化设计，其结论说明改变外载的作用面积以及接触表面粗糙度的变化对接触变形的参数影响不大，而减少底枢间隙可以有效地减少磨损，并且通过曲线拟合，对有限元分析结果进行了简单的二维拟合，可为人字闸门底枢蘑菇头的合理计算与设计提供一定的参考；李林等[11]设计了具有良好人机交互功能的系统软件，为我国同类底枢的设计与维修更换提供精准快捷方法，节省了重新计算与设计的时间。

此外关于底枢摩擦副的数学模型，现有文献均采用赫兹接触模型对其进行分析[9-10]，求得底枢半径、载荷大小、底枢接触间隙与最大接触应力的关系，但赫兹接触模型与底枢的工程实际存在较大偏差。而底枢设计中常采用两种经验公式[12]对底枢应力进行分析，但只是给出底枢蘑菇头半径、外载荷对最大应力的影响，且仅仅反映蘑菇头的局部承压应力。

1 闸门底枢摩擦副接触应力解析模型

蘑菇头材料为线弹性体，采用表面接触力学的Winkler模型进行分析，其特征是蘑菇头仅在荷载作用区域下发生与压力成正比例的变形、在区域外变形为零，即蘑菇头表面上任意一点的变形与该点所承受的压力强度成正比，而与其他点上的压力无关。

在蘑菇头模型上建立球坐标系，如图1所示，为蘑菇头轴线，点为蘑菇头中心。无外载荷时，只有闸门自重，轴与蘑菇头轴线重合；当存在外载荷时，外载荷与轴线偏角为，此时轴与轴线存在偏角。假设(,,)为空间内一点，其球面坐标为(,,)，为原点与点间的距离，为有向线段与轴正向的夹角，为从轴正向看轴按逆时针旋转到点投影在平面上的点所转过的角。

图1 空间球坐标系

无载荷时，取蘑菇头外表面上任意一点,,，为蘑菇头半径。过点取如图2所示的一个微元体123，Δ为在角上的微小增量，Δ为在角上的微小增量。

图2 微元体示意图

蘑菇头受外载荷时，其方向与轴一致，蘑菇头在外载荷作用下沿轴移动Δ，蘑菇头表面受挤压变形，蘑菇头表面微元体面123以同样的方式平移至123，根据几何关系，可得微元体的变形量Δ为：

正应变为：

根据应力－应变的关系，正应力σ（方向指向蘑菇头球心）为：

式中：为蘑菇头弹性模量。

载荷F与接触面上接触应力沿方向的总和平衡，即：

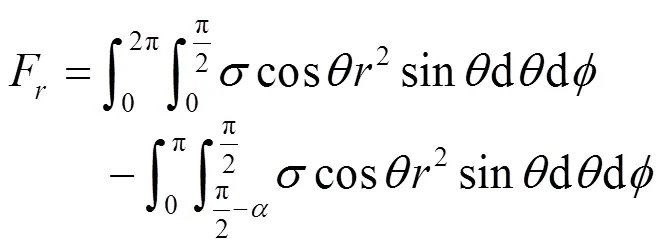
接触面内任意一点的接触应力为：

2 接触应力有限元仿真

理论公式在推导过程中做了很多简化，与实际工况有较大出入，有限元计算可以把实际工况考虑进去，更接近真实值，因此利用有限元分析来验证理论公式合理性。以半径50 mm底枢为例在ANSYS软件中建立模型，进行接触应力分析。底枢配对副材料参数如表1所示。

表1 底枢材料参数

通过ANSYS分析，得到接触面的接触应力分布及理论分布式在-π≤≤π、-π/2－≤≤π/2－的笛卡尔坐标系中的分布如图3～图6中的（a）所示。由图3（b）可知，当外载荷倾角为0°时，最大接触应力出现在蘑菇头几何中心，接触应力随着呈余弦分布，随底枢横截面半径增加而降低，有几何对称性。图3（a）中最大接触应力也出现在蘑菇头几何中心附近，其接触应力分布规律随底枢横截面半径增加而降低，有明显的几何对称性。

由图4（a）可知，当外载荷倾角为10°时，最大接触应力偏离几何中心，出现在外载荷的垂直接触点。接触应力分布有整体偏移，蘑菇头底端外载荷偏角方的接触应力大于另一边。图4（b）中，最大接触应力偏移，接触应力在偏角一侧大于另一侧，规律同理论推导式一致。

图5、图6中，当偏角增大接触应力偏移角增大，最大接触应力减小，有限元分析接触应力分布规律与理论推导式规律一致。

图7为理论值和有限元最大接触应力值。最大接触应力随着外载荷偏角的增大而增加。最大接触应力误差绝对值分别为2.0%、3.2%、13.7%、30.8%。闸门底枢的外载荷偏角一般不超过20°，故有限元分析的最大接触应力与理论值误差可控制在15%以内。理论接触应力计算值都能达到同样的精度，说明理论接触应力公式具有普遍性。

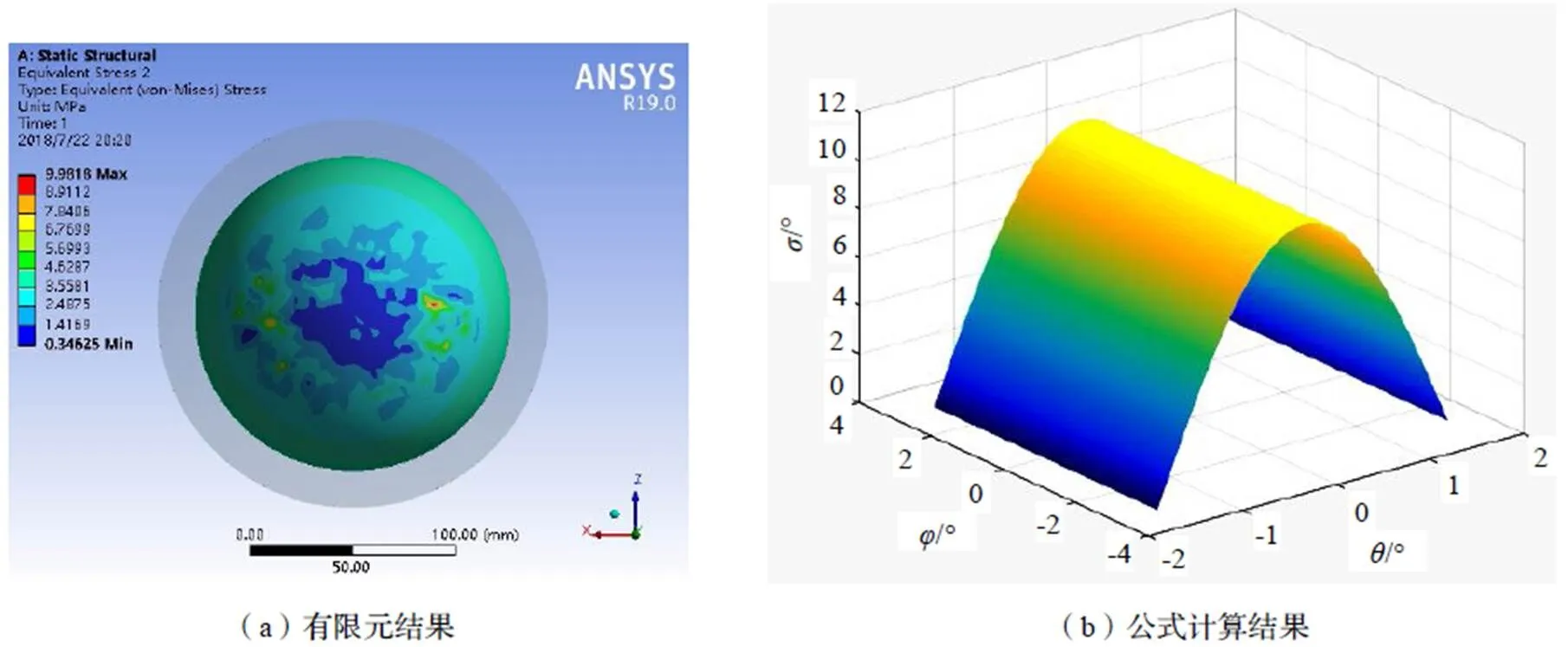
图3 0°蘑菇头接触应力分析结果

图4 10°蘑菇头接触应力分析结果

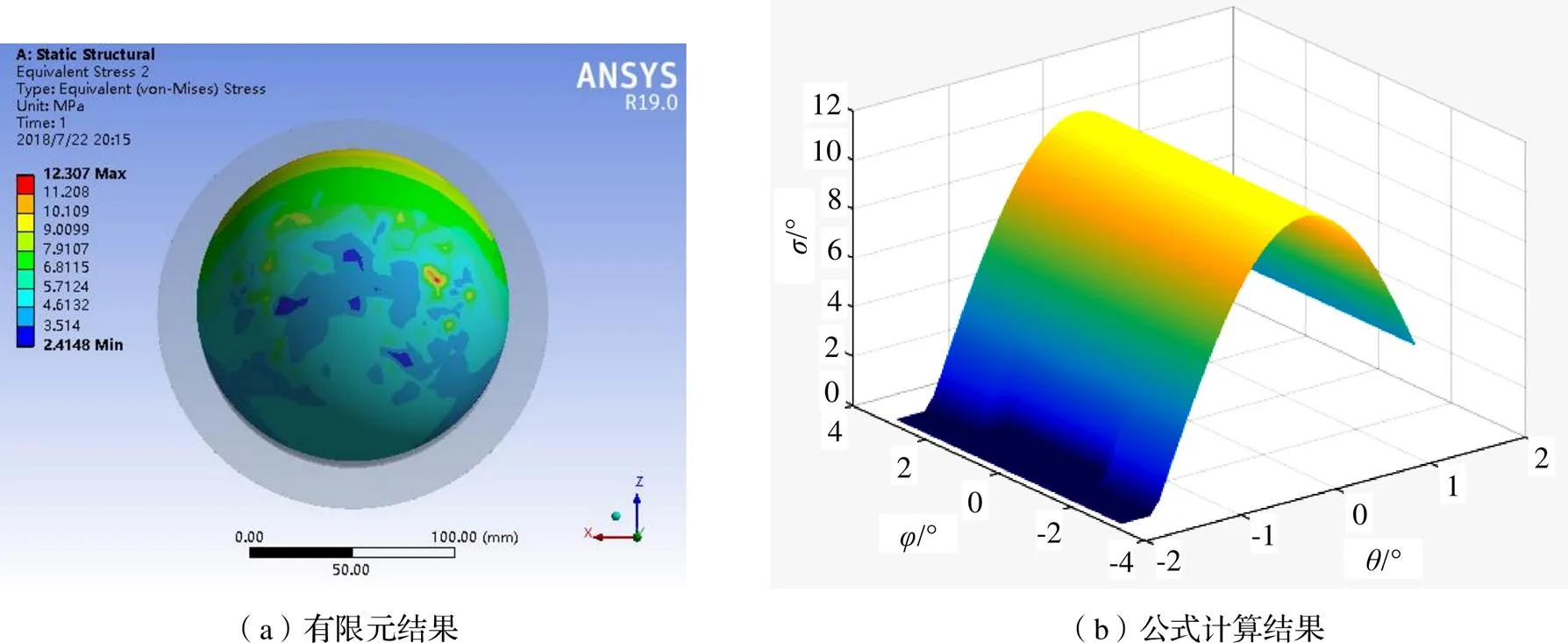
图5 20°蘑菇头接触应力分析结果

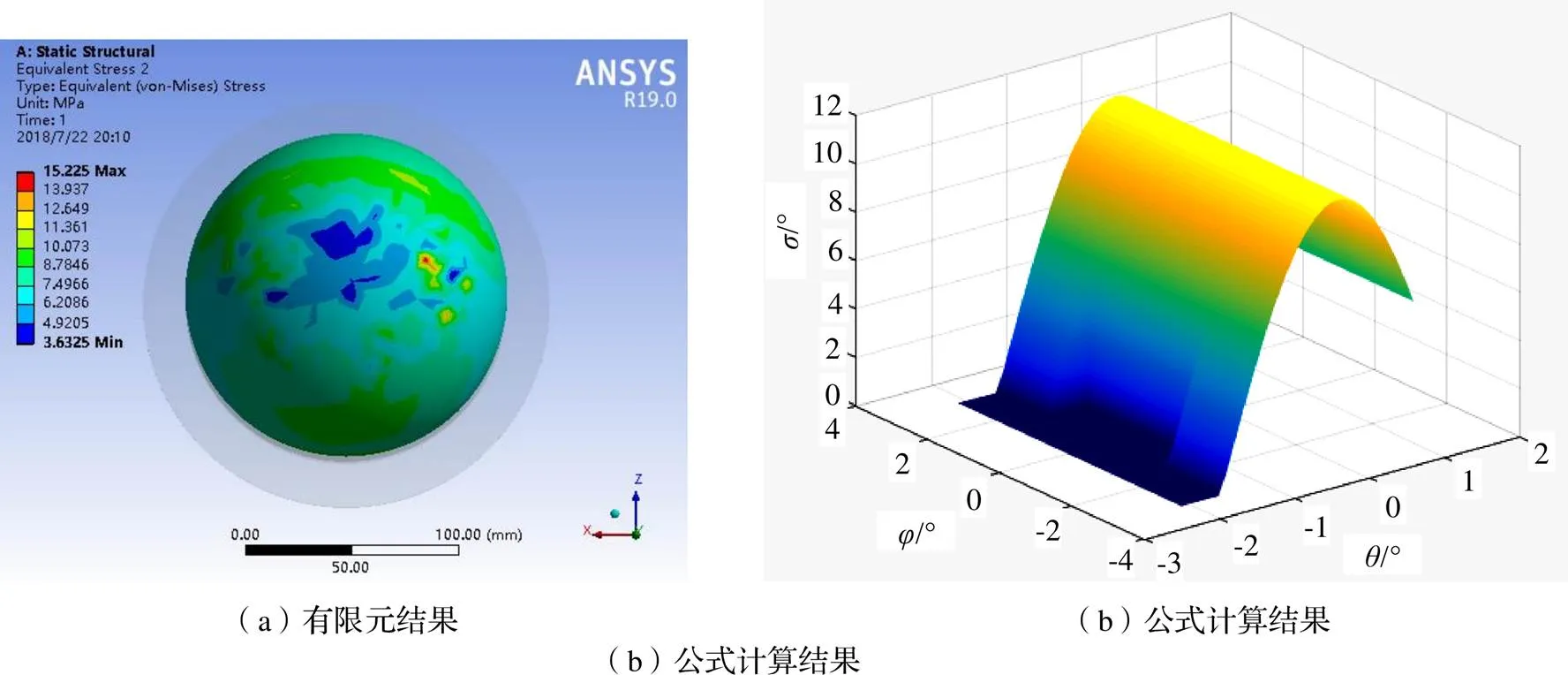
图6 30°蘑菇头接触应力分析结果

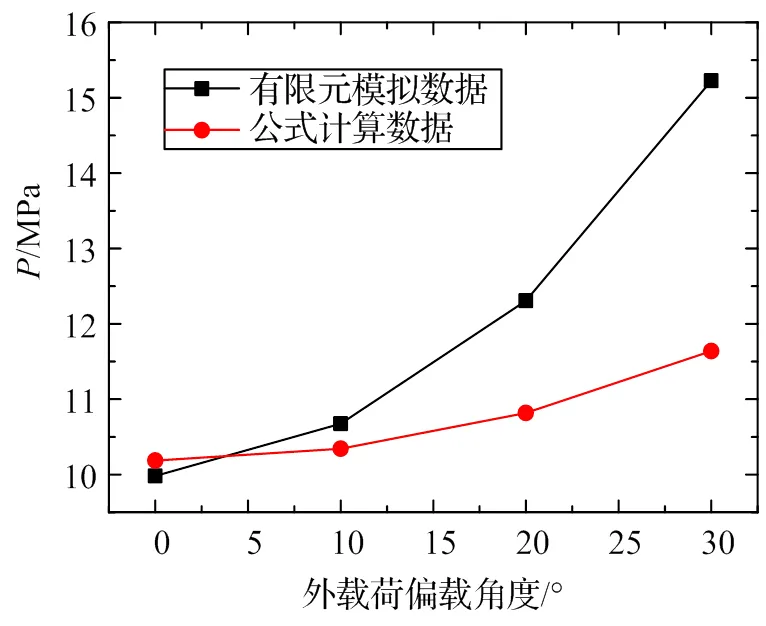
图7 蘑菇头接最大触应力分曲线

3 计算结果与分析

3.1 外载荷对底枢摩擦副接触应力的影响

图8为半径50 mm底枢摩擦副在外荷载倾角10°时，底枢摩擦副接触应力随外荷载大小变化的曲线。最大接触应力随着外荷载的增大而增大，且相同位置点的接触应力也随着外荷载的增大而增大。当外荷载由6 t增大至12 t，增大100%，此时的最大接触应力由3.85 MPa增长至7.70 MPa，增长100%。底枢摩擦副上相同位置点接触应力与外荷载呈正比关系。此时接触应力关于外载荷倾角对称，在底枢摩擦副球面上，非倾角侧外载荷倾角切线周以下即为非接触区域，接触应力为0，外载荷倾角侧一端底枢摩擦副半球面根部，载荷不为0。随着外载荷大小的增加，底枢摩擦副接触应力增长率增大，在15 t时最大接触应力将接近10 MPa。

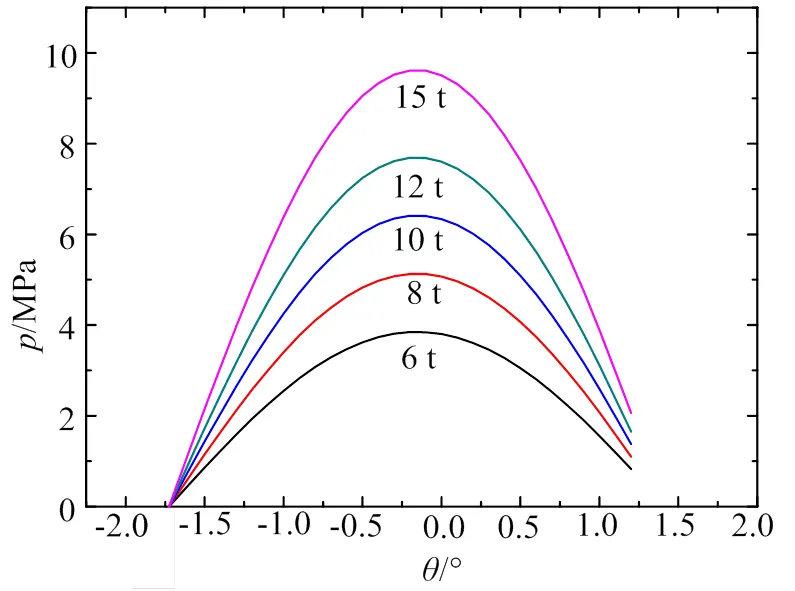
图8 不同外载荷大小下的接触应力

3.2 外载荷倾角对底枢摩擦副接触应力的影响

图9表示当底枢摩擦副半径50 mm、外载荷10 t情况下，底枢倾角变化对接触应力的影响。外载荷倾角增加（由0°增至30°）时，底枢摩擦副最大接触应力分别为6.366 MPa、6.415 MPa、6.477 MPa、6.564 MPa、6.823 MPa。

在非倾角侧，同一位置点接触应力随着外载荷倾角的增大而减小，而倾角侧，同一位置点的接触应力随着外载荷倾角的增大而增大。且当倾角增大时，接触应力的对称区域减小。

故当闸门门体宽度较宽或在风载荷、水载荷明显影响到外载荷倾角时，则最大接触应力增大及应力分布不对称，都应当考虑更高的设计等级。

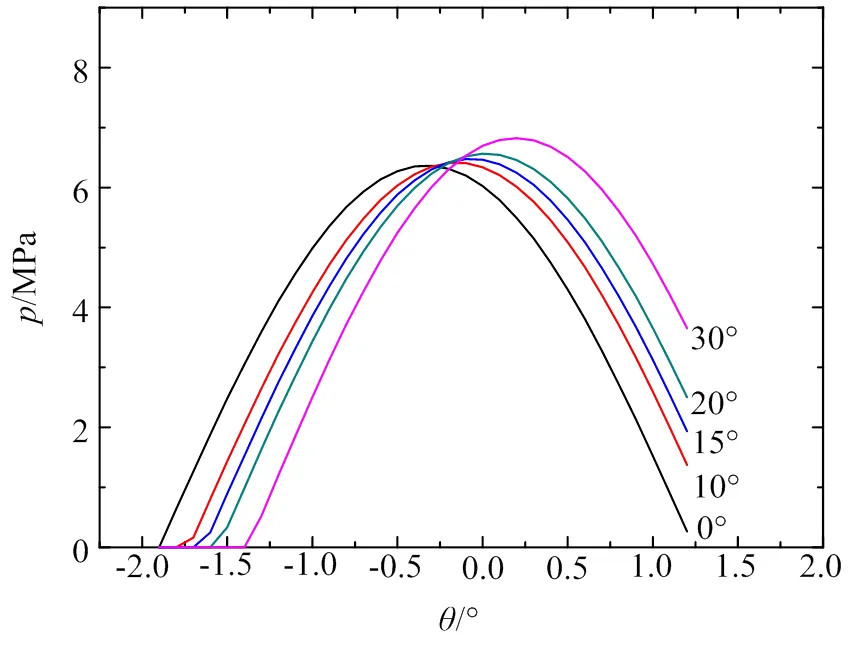
图9 不同外载荷倾角下的接触应力

3.3 底枢半径对底枢摩擦副接触应力的影响

图10为闸门底枢在10°倾角、10 t外载荷条件下时，半径由40 mm增长至80 mm时，接触应力的变化曲线。当底枢半径由40 mm增至60 mm，半径增长50%，最大接触应力由10.02 MPa降至4.45 MPa，降低了55.6%；当底枢半径由60 mm增至80 mm，半径增长33.3%，最大接触应力由4.45 MPa增至2.51 MPa，接触应力降低了43.6%。底枢的最大接触应力随着底枢尺寸的增大而减少，且底枢尺寸半径越小对接触应力的影响越大。此时，接触应力关于外载荷倾角对称，且分布只与外载荷倾角有关，不随底枢半径大小或载荷大小的变化而变化。

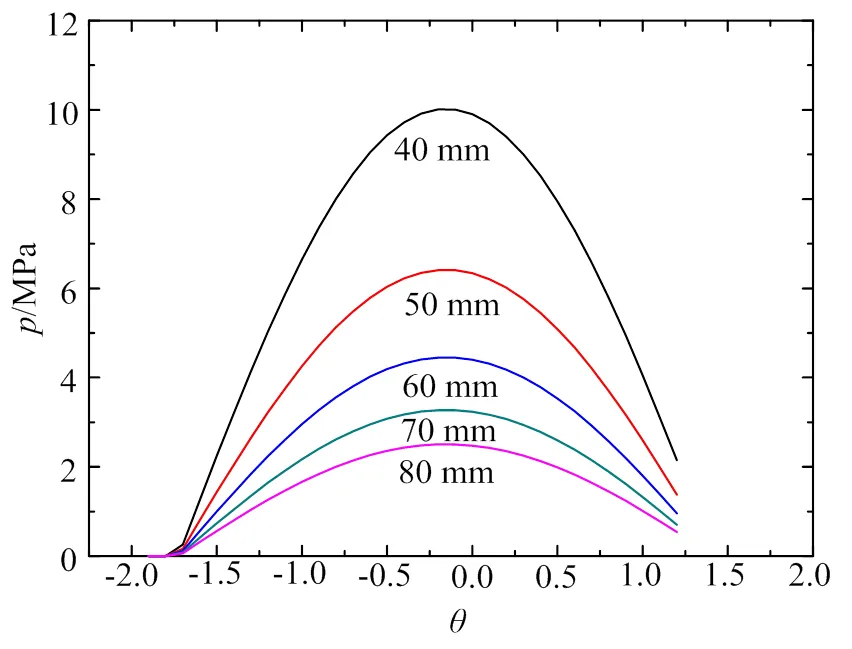
图10 不同半径下的接触应力

4 小结

采用理论推导方法对闸门底枢摩擦副进行接触应力分析，通过有限元分析验证理论公式的精度可知，理论公式在一般的闸门底枢摩擦副上普遍适用。当外载荷偏角＝0～20°，利用理论推到公式计算底枢接触应力值，可以保证受外载荷时接触应力值误差在15%以内。

由理论推导式可知最大接触应力出现在外载荷的垂直接触点。最大接触应力与各点的接触应力随着外载荷的增大而增大，且呈正比关系。接触应力分布关于外载荷倾角有对称分布部分，最大接触应力随着外载荷倾角的增大而增大。闸门底枢半径增大，接触应力减少。

[1]江苏省交通厅航道局. 船闸运转件磨损实验报告[R]. 南京：江苏省交通厅航道局，2001.

[2]司敬阳. 人字闸门底枢结构改进及材料选用[J]. 水利电力机械，2007（2）：11-14.

[3]李玲君，戴振华. 人字闸门固定式底枢改进设计[J]. 水运工程，2019（1）：131-135.

[4]秦红玲，郭文涛，李雪飞，等. 闸门底枢摩擦副QT600-3/40Cr摩擦学性能及磨损表面功率谱密度表征[J]. 机械工程学报，2019，55（17）：1-8.

[5]Jianbin Luo，Shizhu Wen，Ping Huang. Thin film lubrication. Part I. Study on the transition between EHL and thin film lubrication using a relative optical interference intensity technique[J]. Wear，1996，194（1）：107-115.

[6]张元刚，马洪生，钱文君. 运东船闸人字门顶、底枢修理关键技术浅析[J]. 江苏水利，2010（12）：23-24.

[7]陈家伟. 葛洲坝船闸人字门几次重大事故处理及探[J]. 金属结构，1983（2）：36-54.

[8]陈家伟. 葛洲坝2号船闸人字门底枢轴承失效问题探讨[J]. 水电站机电技术，1985（3）：38-43.

[9]岳陆游，丁建宁，杨继昌，等. 船闸蘑菇头和帽接触有限元计算与优化[J]. 农业机械学报，2006（9）：157-160.

[10]殷恋飞. 人字门底枢减摩抗磨结构材料及润滑设计[D]. 镇江：江苏大学，2007.

[11]赵新泽，李林，郭文涛，等. 基于磨损失效评估的人字闸门底枢摩擦副设计软件开发[J/OL]. 机械，2019，46（11）：40-45.

[12]水电站机电设计手册编写组. 水电站机电设计手册金属结构（一）[M]. 北京：水利水电出版社，1988.

Contact Stress Analysis of Friction Pair at the Bottom Hinges of Miter Gate

ZHOU Ziyan

( College of Mechanical & Power Engineering, Three Gorges University, Yichang 443002, China )

The bottom hinges is an important supporting and running part of minter gate, and its wear will cause the failure of minter gate and affect the ship lock function. In this paper, the force analysis of the bottom friction pair of the gate is carried out, and the calculation formula of the contact stress under the self-weight and external load of the gate is deduced. Then the finite element analysis on the contact stress distribution of the mushroom head under its self-weight and external load is carried out with ANSYS software. It turns out that the errors of the theoretical calculation results and the finite element results are small, which proves the rationality of the theoretical formula. The results of this formula indicate that the maximum contact stress occurs at the vertical contact point of the external load. The maximum contact stress and the contact stress at each point increase with the increase of the external load, and are in a proportional relationship; the contact stress distribution is symmetric with respect to the inclination angle of the external load, and the maximum contact stress increases as the inclination angle of the external load increases; the radius of the bottom hinges of the gate increases as the contact stress decreases.

bottom hinges of miter gate；contact stress；theoretical formula

TH16；TH133.31

A

10.3969/j.issn.1006-0316.2020.02.013

1006－0316 (2020) 02－0075－06

2019－07－26

周紫嫣（1994－），女，湖北宜昌人，硕士研究生，主要研究方向为摩擦学。