发动机安装车悬臂梁的设计与优化

王川东，唐宇，殷贵刚，李安成，钱俊宏

发动机安装车悬臂梁的设计与优化

王川东，唐宇，殷贵刚，李安成，钱俊宏

（成都凯迪精工科技有限责任公司，四川 成都 610041）

悬臂梁作为发动机安装车上最重要的承力构件之一，除必须具有足够的强度和刚度之外，同时还要保证质量较轻，最终才能保证发动机安装车的正常使用和安全性。通过分析悬臂梁的工作原理，建立出零件的初步三维模型，通过设定边界条件和添加载荷，利用有限元数值模拟技术进行分析，结果显示强度满足要求、但质量过大，需进一步优化改进。利用Workbench环境中的拓扑优化模块对零件进行形状和尺寸的优化，最终得到了满足强度条件下质量更轻的悬臂梁。经实物称量，该零件的实际质量较设计之前减少了14.25 kg、减幅达51.59%，为今后该类型零件的设计提供一定的参考。

悬臂梁；静力学；强度；优化；ANSYS Workbench

发动机安装车是航空工业领域常用的地面辅助设备，具有多个方向的调节自由度，能够保证发动机在飞机的调试、装配和维修过程中便捷地进行拆装。

悬臂梁作为发动机安装车上最重要的承力构件之一，位于发动机安装车的最上层，呈对称分布，前端（圆柱轴段）与支撑臂连接，中间铰接在支架上，后端与拉力传感器连接在一起，与支撑柱共同分担发动机的全部重量，如图1所示。质量大的悬臂梁构件虽能满足强度和刚度要求，但会导致整个发动机安装车的质量增加，不仅增加了装配人员的劳动强度、造成材料的极大浪费，同时也使得发动机安装车的移动灵活性变差。因此，设计出既能满足强度和刚度要求、同时质量轻便的悬臂梁显得极为重要[1]。本文利用ANSYS Workbench中的拓扑优化模块[2-3]，对最初设计的悬臂梁进行形状优化，根据形状优化的结果，建立全参数化的三维数模，再借助Workbench中的优化模块对各变量尺寸进行优化，最终得到了满足安全系数不小于3的强度条件下质量更轻的悬臂梁。

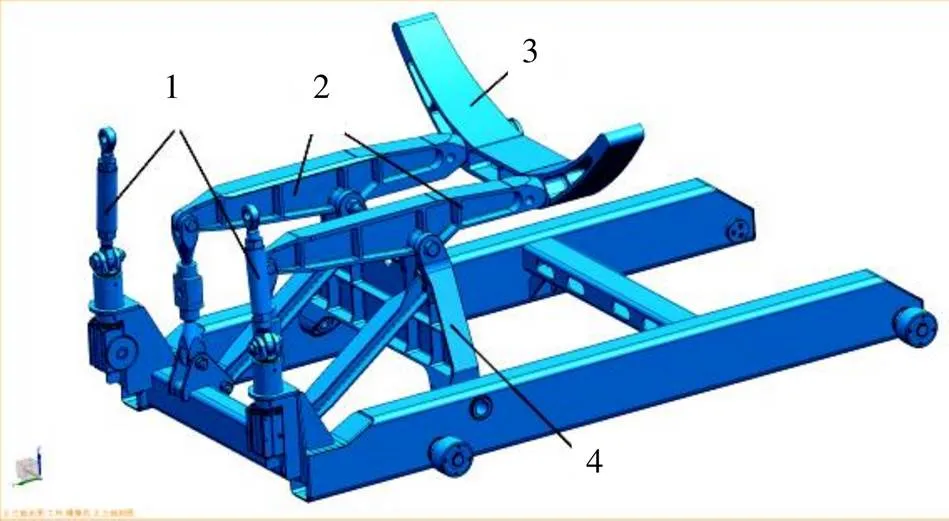
1.支撑柱 2.悬臂梁 3.支撑臂 4.支架

1 静力学分析

1.1 模型的建立

根据悬臂梁的工作原理，绘制出设计构想简图，同时结合该零件与其他构件的配合连接关系，综合人机工程学，借助三维设计软件建立零件的初始三维示意模型，如图2所示。

根据设计要求，悬臂梁采用30CrMnSiA加工制造，查机械设计手册[4]，得到该材料的属性为：杨氏模量＝1.96e+11 N/m2、密度＝7.75e+03 kg/m3、泊松比＝0.2。在三维设计软件中，给零件赋予材料密度后，测量零件的质量约为27.62 kg。

图2 悬臂梁初始模型

1.2 静力学分析

将建立好的初始三维模型通过软件接口导入到ANSYS软件中进行静力学分析，保证了三维模型的一致性，让模拟变得更加真实。

对零件分析发现，整个外形无凸台和凹坑、面与面之间平滑过渡，因此网格划分采用定义网格尺寸的方式进行，综合计算机的性能和网格质量，设置网格尺寸大小为size＝2 mm，划分网格后最终得到5356092个节点、3920443个网格单元。

实时监测悬臂梁的受力大小，工作时前、后段构成一对平衡力，和2个支撑柱一起分担了发动机的全部重量。根据设计任务书阐述，发动机的质量约为1200 kg，因此每根悬臂梁前端所受力约4000 N，经测量，前端受力中面（圆柱段轴向中面）到中间铰接中心面距离为359 mm、后端连接孔中心面与到中间铰接中心面距离为381 mm，由简单理论力学知识计算可知，悬臂梁后端受力约为3769.03 N。中间与支架铰接处添加固定约束，给零件赋予30CrMnSiA的材料属性后进行强度计算，得到悬臂梁的强度计算云图，如图3所示。

可知，初始模型的最大强度为1＝127.8 MPa，查文献[2]得30CrMnSiA的屈服极限为σ＝885 MPa，计算可得安全系数[4]1为：

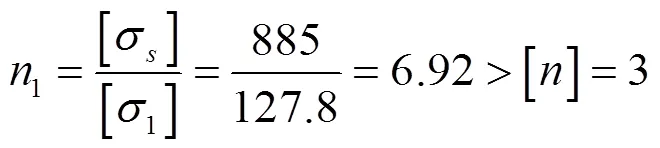
满足安全系数不小于3的设计要求，但此状态下质量过大，需进一步进行优化改进。

2 优化设计

任何机械产品的结构设计都包括结构的总体布局、基本形状和具体尺寸三个方面[5-6]，对应优化问题分别为结构优化设计的拓扑优化、形状优化和尺寸优化三个阶段，而这三个优化问题分别反映在产品的概念设计阶段、基本设计阶段和详细设计阶段完成。

2.1 形状优化

形状优化，又称几何优化，是在拓扑优化的基础之上，对结构的边界形状进行优化，通过优化调整边界几何曲线改变边界形状。

本文借助ANSYS Workbench中的Shape Optimization模块对悬臂梁进行形状优化[6]。材料设置、网格划分和载荷约束和静力学分析过程保持一致，设置优化比例为50%，求解运算，得到悬臂梁的形状优化结果，如图4所示，红色区域为建议删除部分，即对悬臂梁的强度影响较小的区域，灰色部分为建议保留部分，即对悬臂梁的强度影响较大的区域[6-7]。

2.2 尺寸优化

尺寸优化是在结构的拓扑、形状确定之后，针对结构具体尺寸（如加强筋的厚度、宽度和惯性矩等物理量）进行的详细设计[7-8]。

根据悬臂梁的形状优化结果可知，强度影响较小的区域为悬臂梁左右两侧面和圆柱段芯部，因此考虑在零件左右两侧面上对称挖凹槽并设置加强筋、同时在圆柱段芯部钻减轻孔的方式来完成减重。其中零件壁厚、加强筋厚度和减轻孔尺寸的最优数值确定，还需要进行进一步的探究。

图4 形状优化结果

利用三维建模软件，并根据形状优化结果对模型重新进行全参数化建模，并将加强筋的厚度参数变量设置为DS_JB，悬臂梁的中间壁厚参数变量设置为DS_BH（＝悬臂梁总厚度60 mm－凹槽的深度参数变量DS_S），侧面上的减轻孔1的参数变量设置为DS_K1，圆柱轴段上的减轻孔2的参数变量设置为DS_K2。

将参数化建模完成后的三维模型通过无缝关联接口导入ANSYS中进行多目标的优化设计[9-12]。

（1）设定优化目标

将悬臂梁的质量Mass和由Equivalent Stress探测得到的计算结果中最大的强度值Maximum设定为优化目标。

（2）试验设计及灵敏度分析

设定各参数变量的变化范围，如表1所示。设定每个参数变量的采用数目为100，得到设计变量对优化目标的柱状灵敏度图，如图5所示。可知，设计变量DS_JB和DS_S对质量和强度这两个优化目标的敏感性最大，DS_K1对两个优化目标的敏感性最差，DS_K2对两个优化目标的敏感性居于中间。

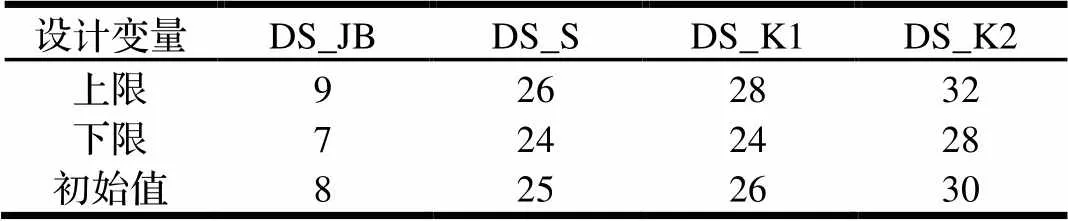
表1 各参数变量的范围（单位：mm）

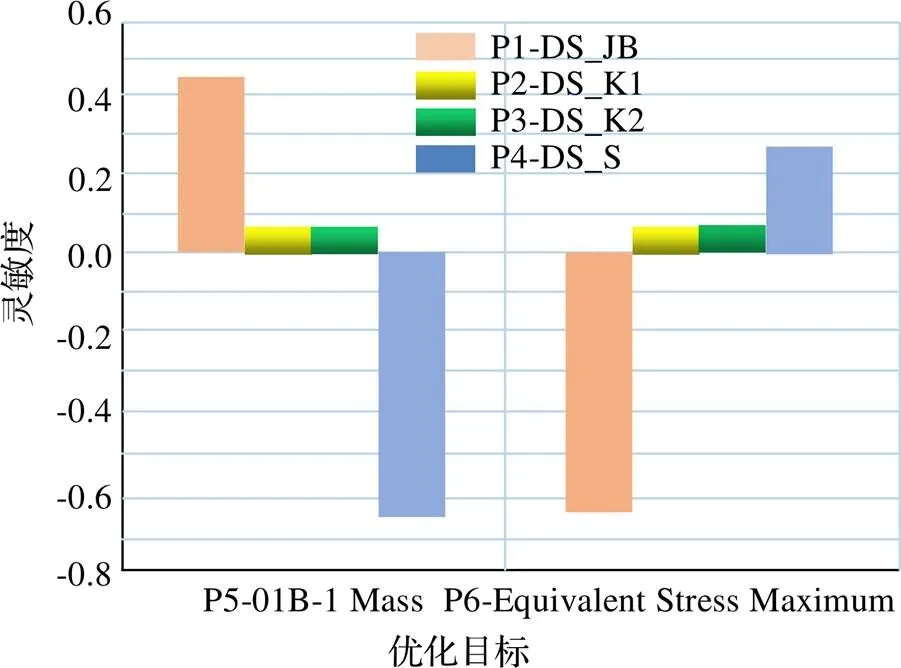
图5 设计变量对优化目标的灵敏度

（3）实施优化并确定最优设计

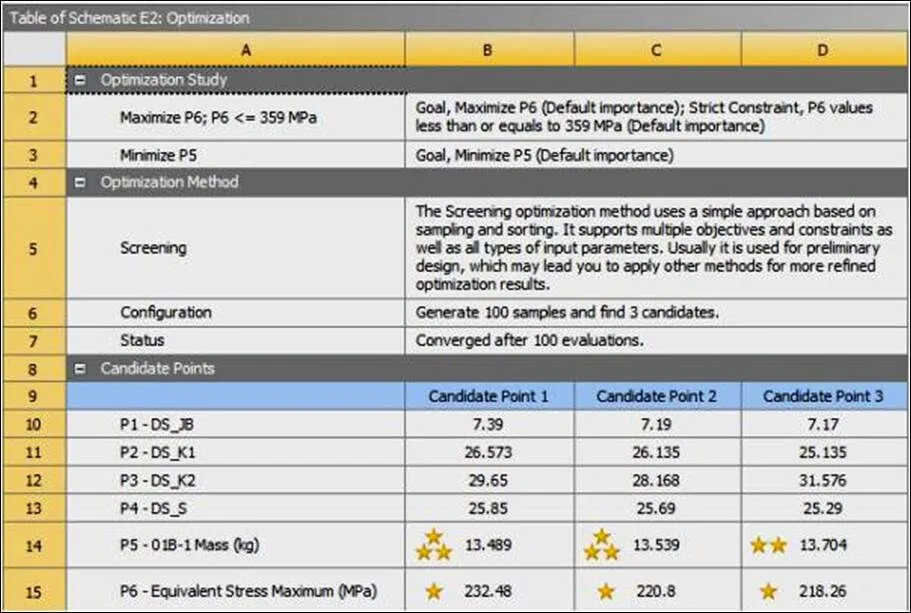
图6 设计变量的优化结果

结合本文研究的目的是在满足强度条件下获得最轻质量的悬臂梁，易知Candidate A为最优方案，此时各参数变量值满足：DS_JB＝7.39 mm，DS_K1＝26.573 mm、DS_K2＝29.65 mm、DS_S＝25.85 mm，得到目标函数最小质量为＝13.489 kg，且此时的强度为2＝232.48 MPa，计算安全系数[4]2为：

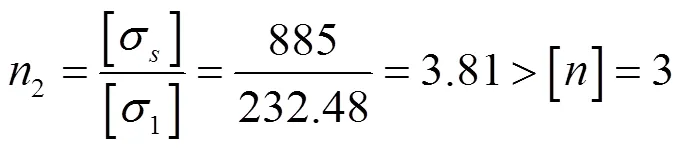
强度仍然满足设计要求，但此时零件的质量较初始值大大减小。根据此优化数据对三维数模进行修改，得到零件最终的三维模型，如图7所示。

3 实物验证

对最终优化过后的零件进行工艺分析，绘制出合理的工艺路线图：备料→预备热处理→铣工规方→超声波探伤→数控粗加工→最终热处理→修基准→数控精加工→车工→数控去工艺头→钳工去毛刺、锐边→磁粉探伤→表面处理→终检→入库。

根据上述工艺路线图，编制出详细的工艺加工文件后进行机械加工，得到悬臂梁的实物，经称量，该零件的实际质量为13.37 kg，较优化设计前减少了14.25 kg、减幅达51.59%。

将生产出的实物通过紧固件装配成部装，再装配到发动机安装车上，如图8所示，通过发动机装机试验测试，满足强度和刚度要求。

图8 发动机安装车部装实物图

4 结论

（1）在产品概念设计阶段，根据悬臂梁的工作原理，结合结构的总体布局，综合人机工程学，建立出零件的初始三维模型。

（2）在初始三维模型基础上，利用ANSYS Workbench软件对零件进行形状优化，找到了对强度影响较小的区域为悬臂梁左右两侧面和圆柱段芯部，即找到了形状优化的方向。

（3）根据形状优化的指导结果，在三维软件中对悬臂梁进行全参数化的建模，在ANSYS Workbench环境中对其进行多目标的优化设计，实现了各变量参数尺寸的最优，达到了在质量最小的情况下保证零件的强度安全系数不小于3的设计要求。

（4）根据最终实物称量，较优化设计前减少了14.25 kg、减幅达51.59%。

本文所述优化设计方法为今后该类型的零件设计提供了一定的参考。

[1]高东强，毛志云，张功学，等. 基于ANSYS Workbench的DVG850工作台拓扑优化[J]. 机械设计与制造，2011（2）：62-63.

[2]陈应飞，尹湘云，王超，等. 基于ANSYS Workbench的高速旋转轴天平动态校准装置的模态与谐响应分析[J]. 机械，2019，46（7）：11-16，35.

[3]许进峰. ANSYS Workbench15.0完全自学一本通[M]. 北京：电子工业出版社，2014.

[4]闻邦椿. 机械设计手册[M]. 北京：机械工业出版社，2010.

[5]徐灏. 安全系数和许用应力[M]. 北京：机械工业出版社，1981.

[6]易军. 小型联合收割机变速箱壳体结构优化与可靠性分析[D]. 成都：西华大学，2016.

[7]何正嘉，李兵，陈雪峰. ANSYS Workbench设计、仿真与优化[M]. 北京：清华大学出版社，2008.

[8]董树东，赵宏建，马力顺，等. 防恐翻板路障机设计与结构优化[J]. 机械设计，2018，35（S1）：297-300.

[9]杨姝. 复杂机械结构拓扑优化若干问题研究[D]. 大连：大连理工大学，2007.

[10]王强. 基于ANSYS Workbench一字型转轴扭矩分析[J]. 机械，2018，45（7）：25-27.

[11]赵海鸣，蒋彬彬，李密. 基于拓扑优化与多目标优化的机床底座结构设计[J]. 机械设计与研究，2018，34（4）：100-105.

[12]毛建中，黄旭. 电动车2AT变速箱壳体拓扑优化与改进设计[J]. 机械强度，2018，40（5）：1118-1124.

Design and Optimization of Cantilever Beam for Engine Installation Car

WANG Chuandong，TANG Yu，YIN Guigang，LI Ancheng，QIAN Junhong

( Chengdu Kaidi Precision Technology Co., Ltd., Chengdu610041, China )

As one of the most important bearing members on the engine installation car, the cantilever beam must have sufficient strength and rigidity, at the same time, which ensure the light weight, so that which finally ensure the normal use and safety of the engine installation car. By analyzing the working principle of the cantilever beam, a preliminary 3D model of the part is established. By setting the boundary conditions and adding the load, the finite element numerical simulation technology is used for the analysis, The results show that the strength meets the requirements, but the quality is too large, and further optimization and improvement are needed. In this paper, the shape and size of the part are optimized by the topology optimization module in the workbench environment, Finally, the cantilever beam with lighter weight is obtained under the condition of strength. After weighing in real thing, the actual quality of the part is reduced by 14.25 kg compared with the design. The reduction rate is 51.59%, which provides a certain reference for the design of such parts in future.

cantilever beam；static structural；strength；optimization；ANSYS Workbench

TH16；TH122

A

10.3969/j.issn.1006-0316.2020.02.011

1006－0316 (2020) 02－0064－05

2019－07－15

四川省科技计划项目（2018GZ0476）

王川东（1989－），男，四川通江人，工学硕士，助理工程师、技术员，主要研究方向为现代机械设计方法及制造技术。