悬浮隧道车辆荷载响应分析与设计方法研究

邹威，林巍 *

（1.中交悬浮隧道结构与设计方法研究攻关组，广东 珠海 519000；2.中交公路规划设计院有限公司，北京 100088）

1 概述

悬浮隧道车辆交通是基本荷载。当在水动力环境弱或无波、流环境建造悬浮隧道时，车辆荷载可能主控设计方案。车辆通过桥梁时产生冲击力，两者发生耦合振动[1]；相比桥梁，悬浮隧道沿程锚固竖向刚度可能更弱，浮筒式悬浮隧道车重由浮力变化平衡，锚索式悬浮隧道由部分管体净浮力补偿。

悬浮隧道交通荷载研究较少。文献[2-3]提出考虑车重、路面不平整和波流因素的力-时程荷载模拟表达式，并借琼洲海峡概念案例计算；文献[4-5]等借上同案例，将水体作用简化为管体横向与竖向阻尼，分析张力腿竖向刚度、移动荷载大小、移动速度、行车间距对管体响应的影响；文献[6]发现流固耦合效应增加动力放大系数，2D与3D模型在隧道受到强约束时较接近，且Morison方程较适用。文献[4-6]均发现增强锚索刚度可减少动力放大系数。文献[7]研究了锚索安全与振动稳定性、锚索材质、水阻尼与结构阻尼及锚索初张力对车辆荷载作用的影响。

本文提出了车速与悬浮隧道结构参数之间更系统的关联，结合案例计算结果，拟合了动力放大系数与结构和车辆交通参数之间的表达式；并首次提出与分析了悬浮隧道车辆荷载扭转问题。

2 悬浮隧道车辆动荷载响应分析

2.1 分析方法与计算模型

采用有限元软件ANSYS建立悬浮隧道-车辆耦合分析模型（图1）。管体采用Beam188梁单元，锚索采用COMBIN14弹簧单元；车辆采用MASS21质量单元和COMBIN14弹簧单元分别模拟单辆车的质量和其减震系统。

图1 悬浮隧道模型外部荷载及约束条件Fig.1 External load and constraint conditionsof the SFT model

基准计算工况模型参数。悬浮隧道管体长度L=1 200 m；横断面简化为圆环形状，外径12.8 m，内径10.8 m；钢筋混凝土弹性模量E=3.6×1010Pa；管体质量连其附加水质量223 000 kg/m；纵向布缆间距h=100 m；单个断面缆索合计竖向刚度k=9.4×106N/m。车辆速度v=10 m/s；车辆重量m=2 000 kg；减震系统刚度K=1.0×1020N/m。

悬浮隧道和车辆耦合计算是通过有限元动力逐步法完成，即通过强制位移（D）将车辆单元移动到管体位置对应的梁单元相应的节点，再通过耦合（CP）将车辆节点与管体梁单元节点通过弹簧连接。计算完成后，删除上述耦合关系（CPDELE），进入下个计算时间步[8]，重复循环。

2.2 工况

悬浮隧道车辆动荷载响应的车辆影响因素有：车速、车重、自身刚度、车间距等；隧道影响因素有：管体长度、质量、抗弯刚度、锚索刚度和布置等。分析其中部分关键因素见表1。研究：1）单辆车匀速通过悬浮隧道时引起管体跨中挠度与其静止停在管体跨中引起的静挠度的比值，后文称为动力放大系数μ；2）不同间距车队通过悬浮隧道时引起的管体跨中垂向最大加速度。

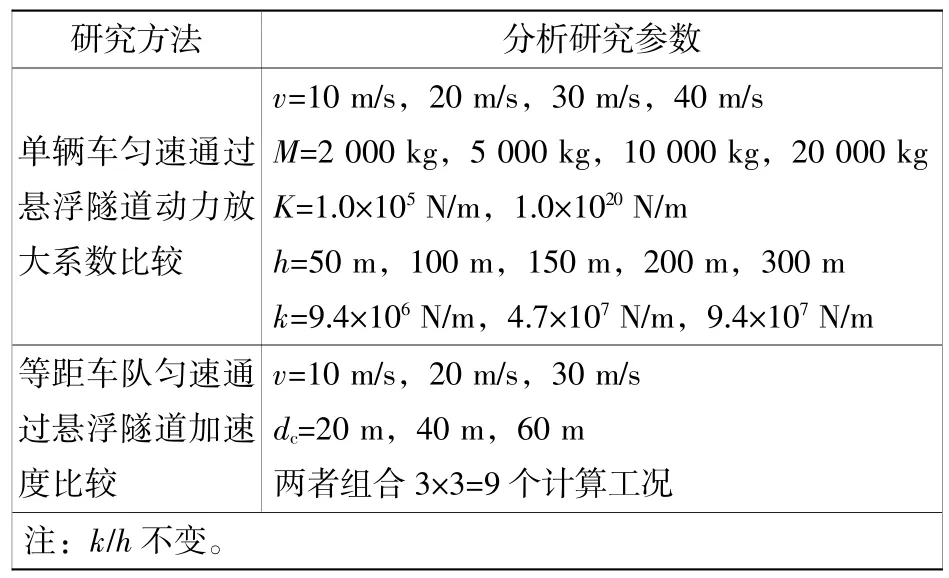
表1 悬浮隧道-车辆耦合模型分析参数工况表Table1 Analysisparametersof SFT-vehicle interaction model

2.3 结果

图2是单辆车不同速度驶过隧道时隧道跨中挠度w时程。图3为不同锚索竖向刚度k时动力系数μ随车速变化。可见随车速增加，动力系数基本呈增加趋势。车速相同时，锚索刚度越大，动力系数越小，且车速越快时该趋势越明显。

图2 不同车速下隧道跨中挠度时程Fig.2 Deflection history of the mid-span section under different vehicle velocity

图3 动力系数μ关于车速v的变化Fig.3 Dynamic coefficientμvarieswith respect to velocity v

其它计算结果概述。1）车辆质量m对动力放大系数影响很小，隧道跨中挠度最大值与车辆质量呈近似线性同向关系，可能因为车辆质量相较于悬浮隧道质量较小。2）布缆间距h改变时，除去间距最大h=300 m工况，其它结果动力系数相同。3）车辆刚度K改变时，对计算结果基本无影响，这可能因为单辆车对隧道作用较小，且本文不研究常规的路面起伏问题。

图4 不同车速或车距跨中加速度时程Fig.4 Acceleration time history of the mid-span section under different vehicle velocity or vehicledistance

图4 是隧道跨中加速度时程计算结果。图5是最大加速度与车速和车距的关系。

可见，1）本研究计算模型车辆对悬浮隧道加速度（舒适性设计）影响小，基本可忽略；2）随着车速增加或车距减小，悬浮隧道跨中加速度增幅较大。

图5 跨中最大加速度与车速和车距的关系Fig.5 Relation between the maximum acceleration of mid-span section with vehiclevelocity and varied spacing

2.4 动力放大系数通用公式拟合研究

研究指出冲击系数与车速和结构自身基频有关[9]，规范也有推荐值[10]。本文进一步指出动力放大系数与该车过隧道的时长（假设平均行驶）和隧道纵面一阶自振周期比值存在直接关联。也即：μ=f（L/（Tv））（1）式中：L为隧道长度；v为车速；L/v也即车过隧道时间；T为结构纵垂面内一阶自振周期。

借2.3节计算结果，拟合式（1），得到式（2），见图6。相关系数R2=0.91。由图可知，当L/（Tv）值较大时，动力系数μ趋近于1。

假定隧道管体两端完全固结，T的计算表达通式见式（3）：

式中：m为隧道管体延米质量；k0为延米刚度；β与约束方式有关，例如固结时为4.73。

将式（3）代入式（2），得到式（4）：

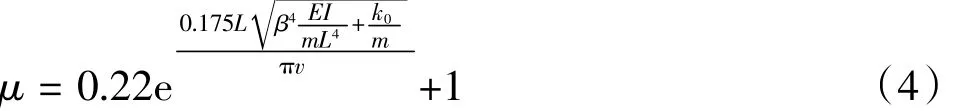
图6 动力系数μ与L/（Tv）关系Fig.6 Relation between dynamic coefficientμand L/（Tv）

3 车辆荷载下悬浮隧道的抗扭评价

3.1 扭转平衡数学模型

本文首次提出车辆在悬浮隧道管体内一侧停靠或行驶而导致的管体扭转问题并在此初步研究。

基于弹性地基梁假设[11]，建立沿着悬浮隧道管体的扭转平衡方程，将悬浮隧道锚固系统简化为等效扭转连续弹簧，计算模型见图7。建立等效弹性基础下悬浮隧道扭转平衡方程（5），假设两端完全固结，方程边界条件见式（6）。解方程得到管体在单侧均布的车辆荷载作用下的沿程扭转角（包含跨中最大扭转角φmax）。

式中：φ为扭转角；x为隧道里程；G为剪切弹性模量；I为极惯性矩；r为锚索绕扭转中心的力臂；为延米刚度；截面扭转非常微小情况下-为锚固系统提供的延米力矩；GI用于估算管体扭转产生的扭力；GI则为微元管段前、后截面的延米力矩差；qk为车辆均布荷载；l为车辆荷载距扭转中心的距离。

图7 截面扭转平衡示意Fig.7 The sketch of the SFT cross-section atthe equilibrium

用建立的模型计算隧道管体沿程扭转角。结果见图8。可知，悬浮隧道横截面的最大扭转角出现在跨中，且随隧道长度增加而增大。但当隧道很长时，例如本算例L=30 000 m时，因沿程锚固系统抗扭力矩与车辆荷载的力矩平衡，跨中附近扭转角基本不变。此时方程（5）代表管体相对扭转的高阶项GI可忽略，简化后跨中的扭转角

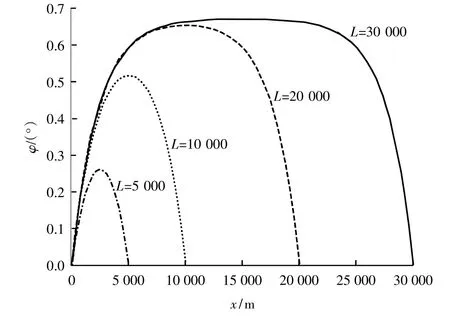
图8 不同长度悬浮隧道截面扭转角的沿轴向变化Fig.8 The cross-section torsion angle of different long SFT varies along the axial direction

3.2 扭转角工程影响评估

假设设计准则为管体挠度不大于L/500或截面最大扭转角不大于0.5°。比较前文算例在悬浮隧道两个车道满布车辆均匀荷载和单个车道满布时结构的挠度和转角。取L=600 m、1 200 m、2 400 m、5 000 m隧道，结果见表2。可见，隧道较长时截面最大转角很可能成为隧道设计控制工况，且车辆单侧通行的情况在现实中也较为常见。

表2 不同长度隧道跨中挠度和转角比较Table2 The comparison of mid-span deflection and rotation of different long SFT

3.3 悬浮隧道管体横断面抗扭能力综合评价

悬浮隧道管体横断面已有多种概念方案[12]，图9中，截面1～截面2与截面3～截面5分别为拟定的2车道和4车道悬浮隧道典型横断面。采用3.1节建立的方法计算不同横断面在单车道满布车辆均匀荷载时的最大扭转角并比较。计算参数及结果总结见表3。可见：1）尽管横断面较宽断面的车辆荷载力臂大，其扭矩大，但是其结构抗扭能力和锚固系统的力臂也大，抗扭刚度相应增强，断面综合抗扭能力需计算确定；2）当隧道很长时，锚固系统抗扭刚度是主控项，断面综合抗扭能力取决于；3）当隧道较短时，横断面结构抗扭刚度是主控项，断面综合抗扭能力取决于；4）就当前计算模型，悬浮隧道管体宽分离式横断面对于单侧车辆荷载工况适应性最佳。

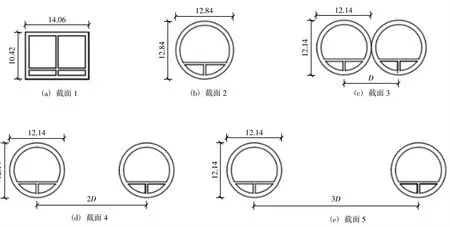
图9 5种不同形式悬浮隧道截面Fig.9 Five different typescross-section of SFT

表3 不同形式截面悬浮隧道最大扭转计算比较Table3 The comparison of maximum torsion angle of the SFT with different sections

4 结论与展望

本文提出移动车辆荷载的动力放大系数与车过隧道时长的直接关联，后者的效用类似循环荷载频率与结构基频之比。对于本研究算例，车辆荷载对悬浮隧道加速度影响很小，车速增加或车距减小时跨中加速度明显增加，但引起的管体加速度值相比人体能感知到的量级（如0.5 m/s）基本可忽略。车辆单侧行驶导致的隧道扭转问题不应忽略，可能成为结构设计控制工况。不同横断面过车抗扭效应取决于锚索布置、车道位置、结构抗扭刚度，所以应进行详细分析比选。

需进一步研究问题：1）基于实测数据的非理想等间距车谱作用下悬浮隧道响应研究；2）单向交通过隧道时（例如水体两端分别是住宅区和办公区，上班时段车辆仅从隧道一端到另一端，下班时相反）引起的扭转加速度研究。

未来，无人驾驶可能将改变传统对隧道内车速和车间距及车重分布密度的认知，分析方法需要重新评估。