线性插值法估算年径流总量控制率误差分析
2020-04-13刘鹏飞黄仕元李赢杰
刘鹏飞,黄仕元,刘 慧,李赢杰,黄 筱
(1.南华大学建筑学院,湖南 衡阳 421001;2.南华大学土木工程学院,湖南 衡阳 421001)
年径流总量控制率作为海绵城市低影响模块的主要管控指标,在国内外一直受到广泛关注,其数值精确程度直接决定着规划层面的现状评估[1]、管控指标分解[2- 5]、目标核算[6]等各项工作能否切实展开。为此,刘慧[7]等人基于5%步长控制率,提出利用线性插值法能够快速准确估算更为精细的年径流总量控制率与设计降雨量的结论,但该研究选择的城市太过单一,实际可推广性与普遍适用性尚需探讨。因此,根据《海绵城市建设技术指南——低影响开发雨水系统构建(试行)》(以下简称《指南》)中提到的年径流总量控制率五大分区图,每区选定2座城市共10座城市作为误差分析对象,利用线性插值法对这10座城市1%步长的年径流总量控制率进行估算,并将得到的估算值与近30a逐日降雨数据统计得来的实际年径流总量控制率进行对比分析。
1 线性插值法估算年径流总量控制率与设计降雨量计算简介
1.1 《指南》统计法
《指南》中提出了确定年径流总量控制率的具体方法,根据中国气象站的气候资料,选取研究区域近30a逐日降雨数据,排除其中小于等于2mm的日降雨数据,将剩余的日降雨数据按由小到大顺序排列,以某一降雨量为标准,低于该降雨数值的以实际降雨数值计算总降雨量,高于该降雨数值的以此降雨数值计算总降雨量,两者之和与实际总降雨量的比值就是年径流总量控制率[8- 9],与年径流总量控制率对应的降雨日值就是设计降雨量。此外,《指南》中还指出,考虑到不同城市的自然条件各异,降雨特征因此也有所差别,年径流总量控制率与对应的设计降雨量应当单独推算。现在大部分省份在编制《海绵城市建设技术导则》时,主要列举了5步长的年径流总量控制率作为指导规划的相应指标。
1.2 线性插值法
线性差值法通常被用来补充不同数值的间隔部分,利用两个已知点的对应值推算两点之间某一点的对应值,因能保证在相应节点上的差值准确率接近100%且比其他插值法更为简便,因此在各个专业领域被广泛采用。如图1所示。
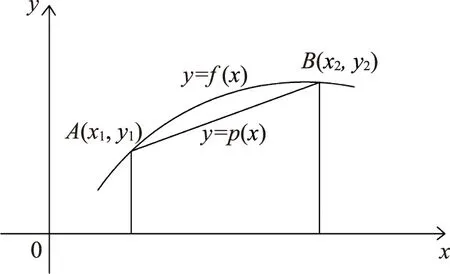
图1 线性差值法
图1中,点A(X1,Y1)与点B(X2,Y2)对应数值已知,要求A、B两点之间任意一点对应的数值C(X,Y),计算方程可表示为:
(1)
根据式(1),可以得到年径流总量控制率的推导式(2):
(2)
式中,Y、Y1、Y2—年径流总量控制率,Y1、Y2是已知值,Y2是Y1的上级,Y是Y1、Y2之间待推算的中间值;X、X1、X2—设计降雨量,X1、X2是已知值,X2是X1的上级,X是X1、X2之间待推算的中间值。
1.3 线性插值法的优势
1.3.1线性差值法估算精度较高
在海绵城市规划编制过程中,需要更加精确的年径流总量控制率及对应的设计降雨量,现行的5%步长年径流总量控制率并不能完全满足相关工作的需要。例如依靠《指南》中提到的容积法计算不同地块现状年径流总量控制率,得到的实际设计降雨量无法与公布的5%步长年径流总量控制率相匹配,这就需要利用近30a的日降雨数据重新计算。在没有时间、资料重新计算的前提下,线性差值法可以基于5%步长的年径流总量管控率计算出精度更高的数据,从而弥补了5%步长年径流总量控制率精度不够的问题。
1.3.2线性插值法不需要获取近30a的日降雨数据
近30a逐日降雨数据可以从国家气象信息中心网《中国地面气候资料日值数据集(V3.0)》获取,该数据集包含了中国近700个基本气象站自1951年1月以来的气压、气温、降水量、蒸发量、相对湿度、风向风速、日照时数和0cm地温要素的日值数据,但相应数据的获取却有诸多困难。首先仅限在教育科研实名注册过的并且拥有省级以上相关科研项目的用户才可以下载,其次699个基准、基本气象站的日数据仅包含部分城市。而线性插值法只需要上下级的年径流总量控制率就可以计算出需要的数据。
1.3.3线性插值法估算年径流总量控制率快捷便利,工作量小
即使获取了近30a的日降雨数据,但由于数据量高达上万条,并且原始数据没经过分类处理,需要借助统计软件一步步的进行整理计算,这个过程耗时耗力,在现实中可实施性不强,容易降低整体工作效率或者主观估算,针对这个问题,线性插值法可以在保证准确率的前提下极大的提高工作效率,降低现实规划设计的工作量。
1.4 线性线性插值法在年径流总量控制率方面的研究存在不足
目前关于线性插值法应用于年径流总量控制率方面的研究较为单一,刘慧等人对萍乡市莲花县1%步长的年径流总量控制率与设计降雨量进行估算分析,认为利用线性插值法能够快速准确的估算更为精细的年径流总量控制率与设计降雨量,但其研究选择的城市太过单一,成果的地域性较强,其实际可推广性与普适性尚需探讨。
2 线性插值法估算年径流总量控制率误差分析
2.1 样本选择
我国幅员辽阔,不同地区的气候、地形、土壤等天然条件与经济条件地域性差异较大,因而不同地区需要确定不同的年径流总量控制指标。针对这个问题,《指南》通过对我国近200多个城市多年日降雨数据统计分析,将我国大陆地区年径流管控率划分为5大区域。为确保研究对象具有代表性,研究结果更加可靠,基于《指南》年径流总量控制率分区图,如图2所示,每个分区选择2个城市作为误差分析对象。一区:乌鲁木齐,拉萨;二区:哈尔滨,昆明;三区:北京、贵阳;四区:武汉、清远;五区:深圳、海口。借助线性插值法对各城市1%步长的年径流总量控制率进行估算,并与《指南》统计法得来的实际值进行对比分析。
2.2 城市近30年逐日降雨数据的获取及处理
从国家气象信息中心网中获取10个城市1981—2018年的逐日降雨数据。对原始数据进行初步处理,去掉2mm及以下的日降雨数据,按照《指南》中的统计法进行计算,得出10个城市5%步长的实际年径流总量控制率与设计降雨量,具体数值见表1(由于《指南》是2014年发布,本文数据采用1981—2018年的新数据,部分数值与《指南》会有些许偏差,但绝大部分数值吻合)。受篇幅所限,更小步长的控制率与设计降雨量不做详细展示,部分具体数值会在误差分析中展出。
2.3 线性插值法估算各城市管控率及设计降雨量
在实际规划编制中,常常会计算一个地块的实
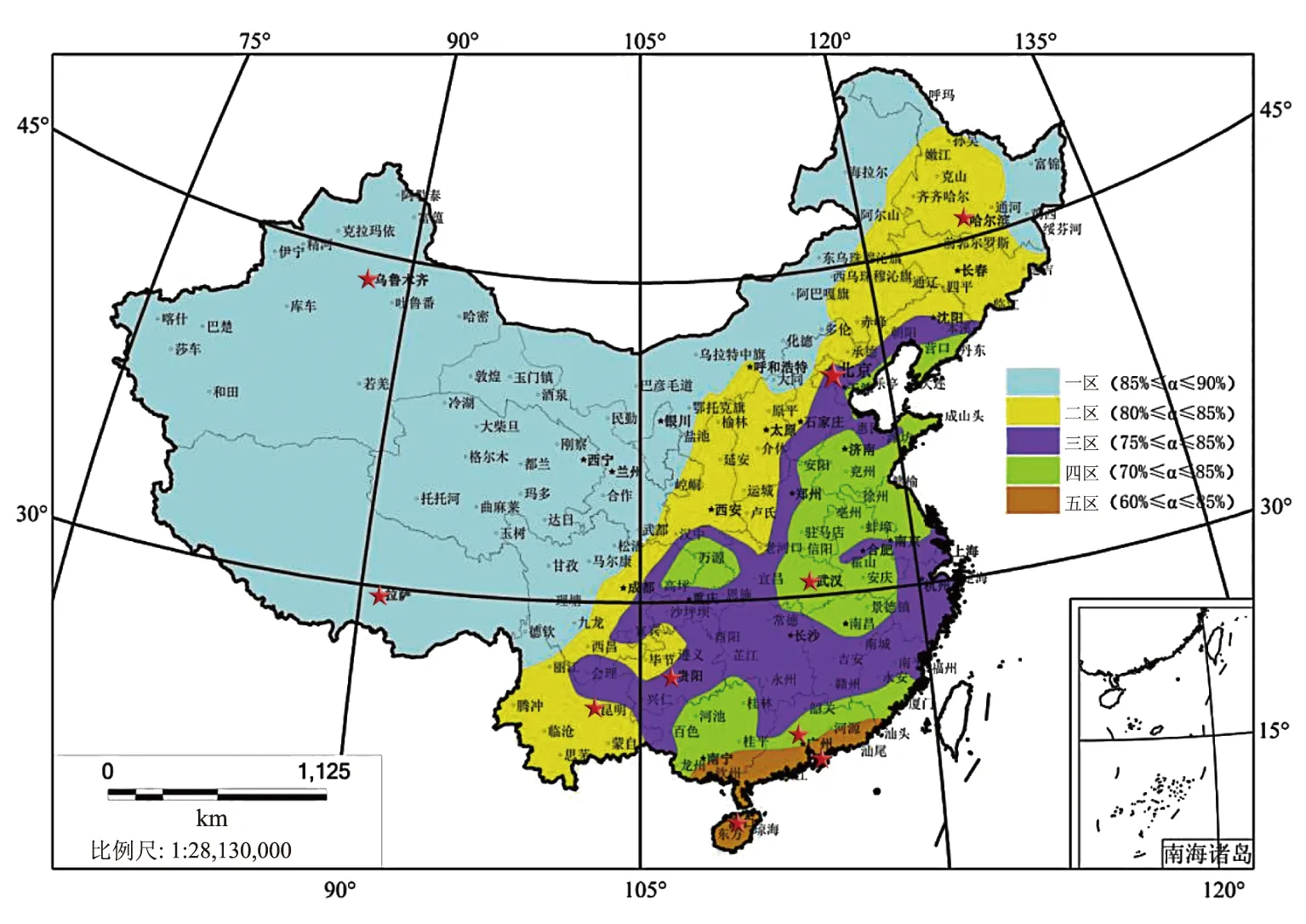
图2 年径流总量控制率分区图
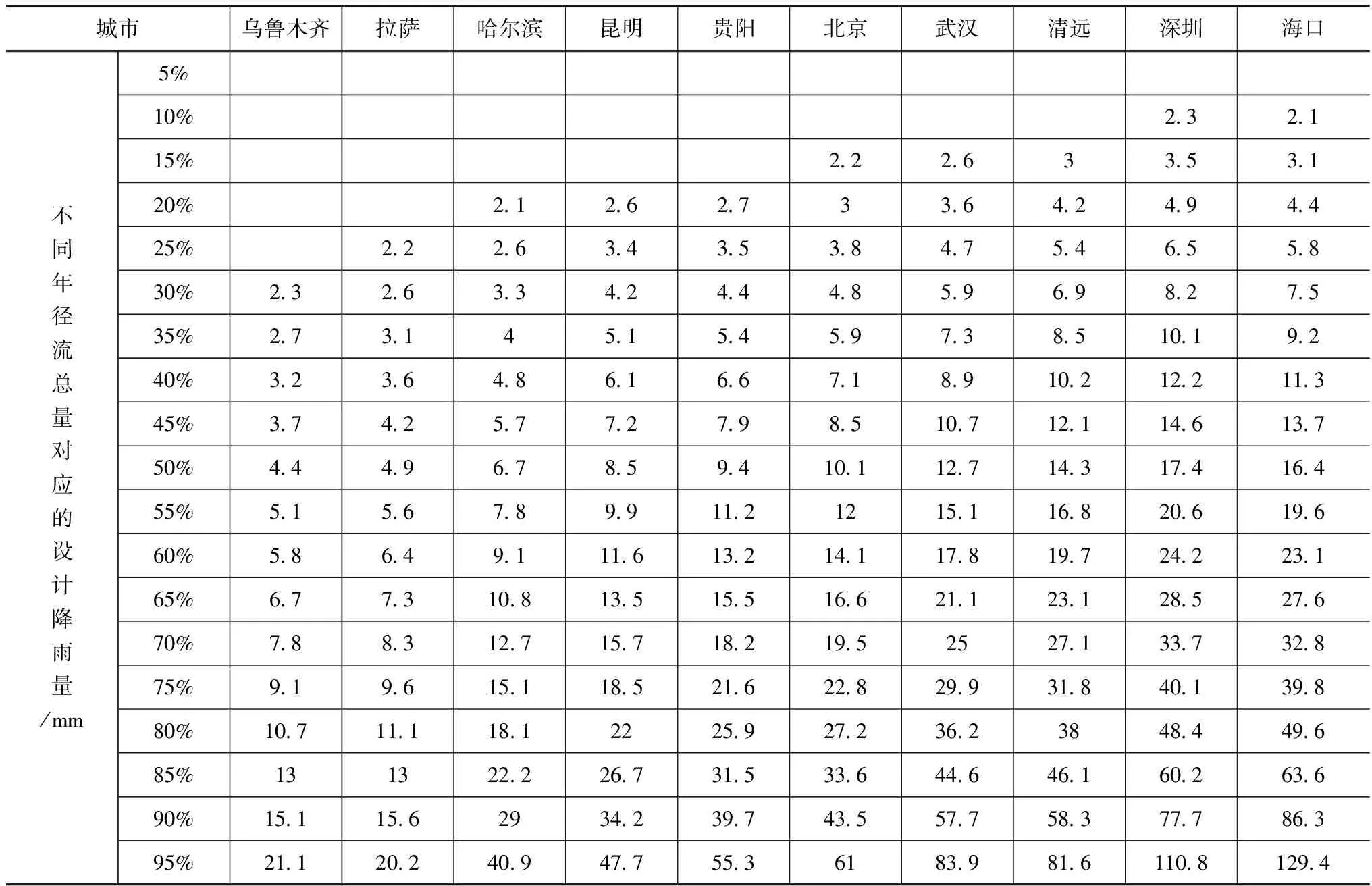
表1 10个城市年径流总量控制率对应的设计降雨量取值表
际设计降雨量,找出相应的实际年径流总量控制率作为规划指标参考。以海口为例,如果按照《指南》中的容积法计算出海口市某地块的实际设计降雨量为34mm,则无法通过相关导则找到对应的实际年径流总量控制率,这时候可以用线性插值法根据已有的数据及式(2)估算出对应数值。同理,也可以根据年径流管控率估算出对应的设计降雨量。
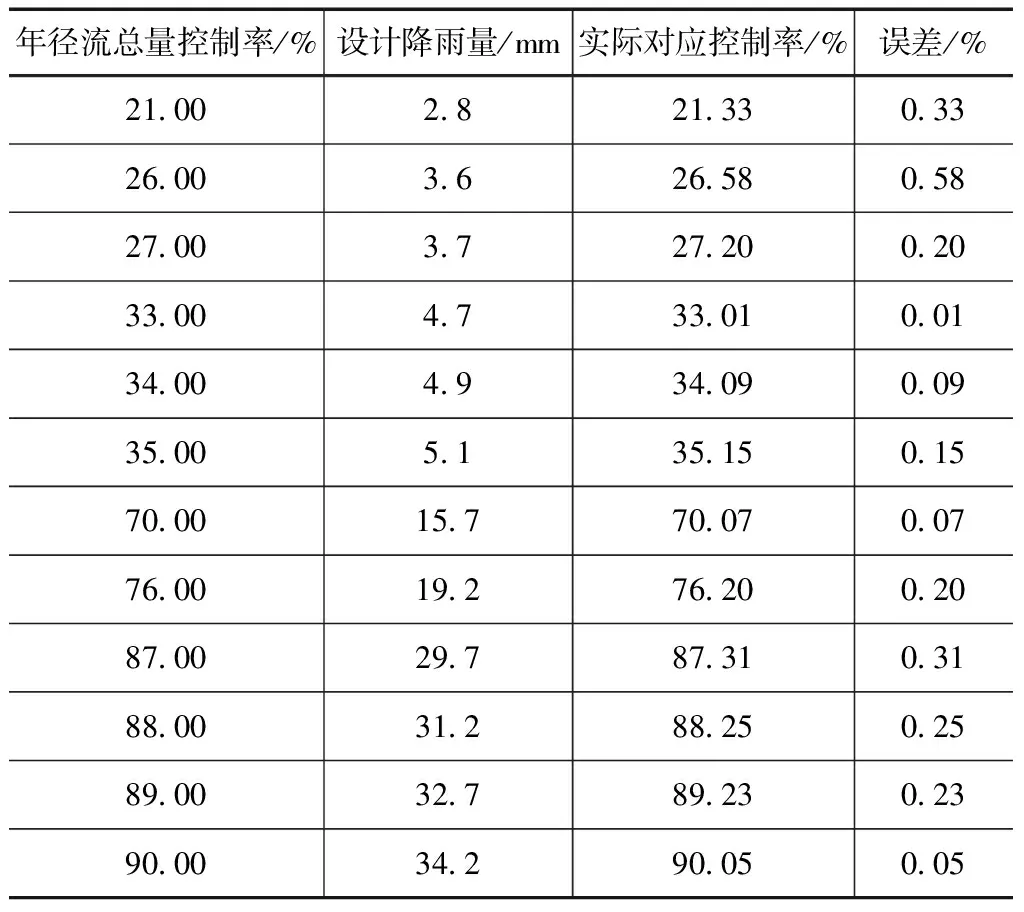
表2 昆明市1%步长年径流总量控制率与设计降雨量估算分析表
按照式(1)、(2),根据各城市5%步长的年径流管控率及设计降雨量估算出1%步长的成果,由于数据量巨大,以二区城市昆明为代表,其他各区的城市类似。
2.4 误差分析
为验证线性插值法是否适合大部分地区,需对估算结果及实际值进行误差分析。以表2为例,昆明在《指南》中属于径流总量管控率二区,在年径流总量控制率21%~90%区间中,设计降雨量3.6mm对应的估算值与实际值误差最大,差值为0.58%,平均误差为0.19%。其他各区城市的误差分析见表3。
通过表3可以看出一区城市的平均误差最大,误差分别为0.36%、0.28%;五区城市的平均误差最低,误差分别为0.11%、0.12%,说明线性插值法并不是适用于所有城市,处于一区的城市平均误差值过高,不建议使用线性插值法进行相关估算;一区到五区城市平均误差值呈现阶梯下降的趋势,究其原因是一区到五区的降雨量呈现上升趋势,五区的日降雨数值要丰富于一区的日降雨数值;数据量大、数值丰富的地区计算波动小,数据量小,数值单一的地区计算波动大。
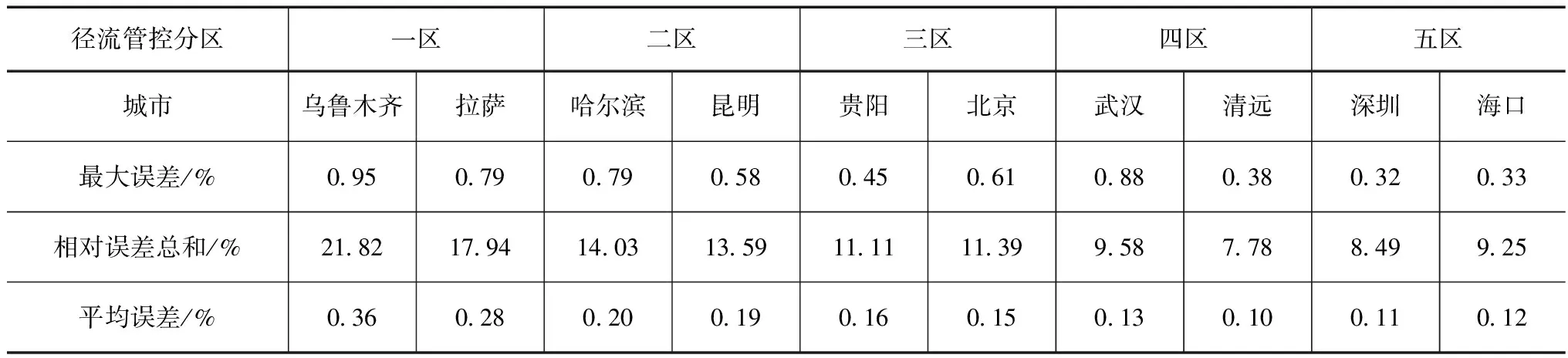
表3 各径流管控区城市的相关误差分析
3 结语
本文基于五大分区10座城市近30a逐日降雨数据对线性插值法是否具有普适性进行误差分析。结果表明:处于第一分区的城市不适宜用线性插值法进行相关估算,对于其他分区,尤其是处于第五分区的城市,线性插值法更具有实际推广意义;线性插值法更适用于日降雨数值多且数据丰富的区域。其他学者在此基础上可以探索一种适用于一区城市径流管控率的快速估算方法。
