高密度环境下的脉冲分选技术研究

吕新正，张 敏

（中国电子科技集团公司第38研究所，安徽合肥230088）

0 引言

脉冲分选是从随机交叠的脉冲流中将来源于不同目标的脉冲串进行分离，并将脉冲串按所属目标辐射源进行归类的过程。分选结果的好坏关系到后续辐射源识别、威胁判断、干扰决策的过程，并直接影响ELINT、ESM、RWR等电子战装备的性能指标。因此，脉冲分选技术是电子对抗领域中的一项关键技术，已经成为衡量电子战侦察设备能力的重要标志。随着雷达技术发展和大量新体制雷达的部署应用，雷达对抗侦察系统面临的信号环境日趋密集、复杂，给传统的脉冲分选架构和分选方法带来了巨大挑战。

目前的脉冲分选技术主要分两级处理，首先根据到达方向(DOA)、频率（FREQ）、脉宽（PW）等参数对雷达信号进行预处理，然后利用脉冲重复间隔(PRI)对信号进行进一步分选处理。预处理常采用聚类的方法实现脉冲信号的初步处理，根据方位、频率、脉宽参数将大量的脉冲描述字（PDW）聚类成多个中心[1-2]。分选处理采用到达时间（TOA）进行脉冲重复间隔估计和去交织，主要包括累积差直方图法[3]、序列差直方图法[4]、PRI变换方法[5]，

其中直方图统计的方法都是以计算脉冲到达时间的自相关函数为基础，容易出现“谐波”，而且对抖动信号效果不理想，但因其运算速度较快，在工程中得到大量应用。PRI变换可以抑制谐波，而且可以检测抖动信号，但因其需要进行大量的指数运算和复数运算，难以达到实时性要求。

本文分析了雷达信号的时域、频域、空域特性，首先采用基于脉冲描述字中的方位、频率、脉宽进行聚类，对高密度脉冲进行稀释处理，然后采用一种新的分选方法进行时序分析，新方法同时兼顾直方图方法和PRI变换算法的优点，并采用多DSP并行处理的方法提高了算法的运行速度，从而保证了高密度环境下实时分选的性能和速度，在实际处理中有一定的应用价值。

1 高密度环境下的脉冲分选技术

随着战争环境的日益复杂，空间的电磁信号越来越多，有时达到每秒上百万个脉冲信号，如果采用常规的处理方法，处理的数据量非常庞大，无法达到实时处理的要求。从工程角度考虑，实时性非常重要，因此为了做到实时处理，需要对庞大的数据流进行稀释，稀释会带来信息的丢失，但通过频率稀释的办法可以将丢失的信息降低最低。从分选的角度讲，识别一批雷达目标只需要几十个脉冲，最少时只需要几个脉冲，而在侦察时间内可收集到成千上万个脉冲，因此合适的稀释方法可以不丢失目标的信息。

1.1 脉冲稀释技术

对于电子对抗系统来说，往往需要侦察的信号带宽较宽，往往到达几千兆到几万兆，而对于雷达信号，即使是捷变频信号，其带宽也只有几百兆，因此同时接收到的信号会在不同的频率点有分布，这为频域上稀释提供了条件；对于空间信号来说，其作用的空间范围往往在方位均有几十度，而目前测角精度可以达到1°以下，这说明可以从空间上进行稀释；对于脉宽信号，其变化范围也有几百微秒，对于脉宽测量误差0.1 μs的系统来说，也可以从脉宽上进行稀释。图1为基于方位、频率、脉宽的三维聚类仿真图，从图中可以看出，通过不同参数的凝聚可以起到脉冲稀释的作用。

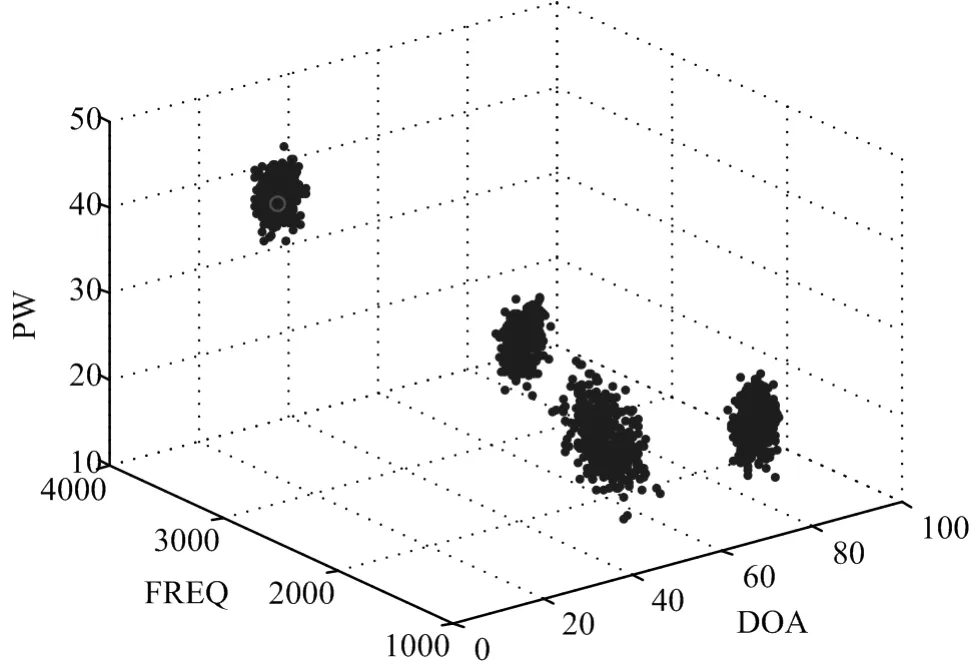
图1 基于方位；频率、脉宽的三维聚类仿真图

假设脉冲密度为每秒200万个脉冲，共有50批目标，则每批目标4万个脉冲，对于一批目标，即使很复杂的目标类型，有效脉冲个数也只需要上百个就能正确分选出目标，考虑到聚类后同时存在多批目标的情况，能正确分选的脉冲个数也不到1000个。因此，设定图1为基于方位、频率、脉宽的三维聚类仿真图，聚类后脉冲个数最大为1024个，50批目标共5万多个，因此，对于脉冲密度为200万个脉冲的实时处理系统，只需要每秒处理5万个脉冲分选就能满足系统实时处理要求。从上面的分析也可以看出，稀释程度取决于聚类后脉冲的目标批数，如果只有一批目标，那只需要处理1024个脉冲就能分选出目标的特征参数。图2为高密度环境下脉冲稀释处理流程图。

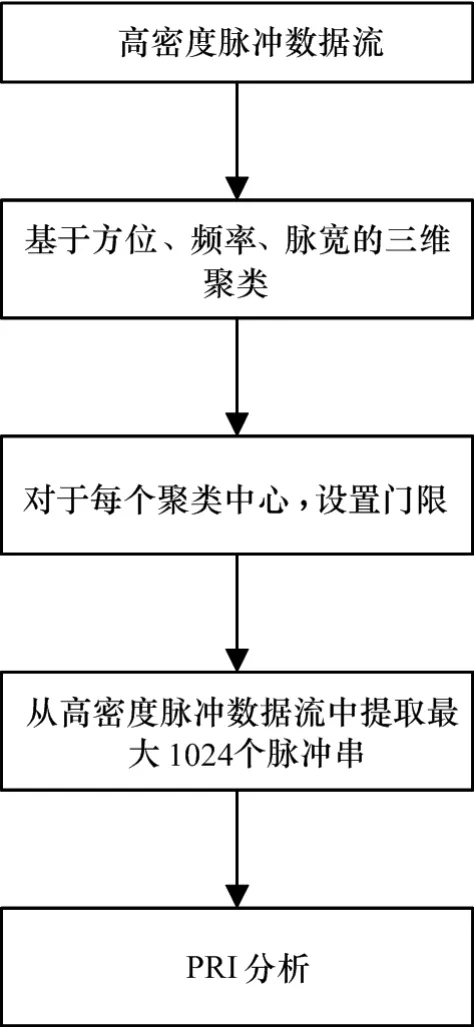
图2为高密度环境下脉冲稀释处理流程图

1.2 PRI分析技术

基于TOA的时序处理目前主要采用两种方式，一种是基于直方图的方法，另一种是基于PRI变换的方法。

脉冲到达时间可以用脉冲前沿时间表示，脉冲串模型可以化为单位冲击函数和，TOA序列可以表示为：

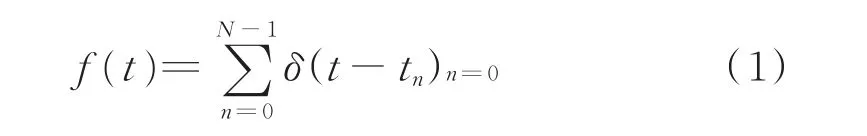
式中，δ(·)为狄拉克函数，tn表示观测时间T内第n个脉冲的TOA，N表示观测时间T内到达脉冲的总数，则f(t)的自相关函数可以写成：

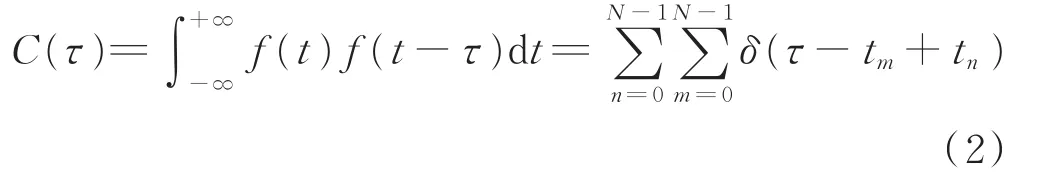
式中，τ=tm-tn，对 C(τ)在区间[τ1,τ2]上进行积分可得：

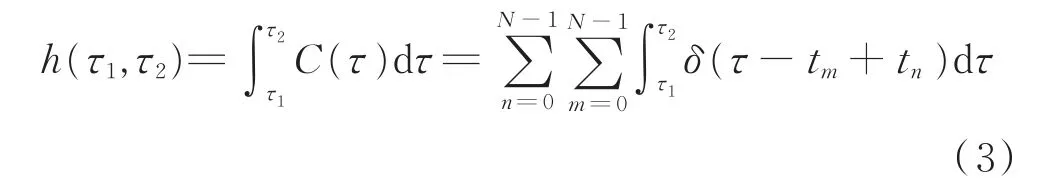
由式（3）可知，h(τ1,τ2)可看作脉冲串落入[τ1,τ2]的次数。

假设脉冲串的PRI固定为ψ，考虑到在观察时间T内辐射源脉冲数为N个脉冲，所以有(N-1)ψ≤T。在计算直方图图时，往往将观察时间T等分为L个长度，则定义直方图的箱长为bτ=T/L，第k个PRI箱的中心为：

因此，直方图门限可以设置为：

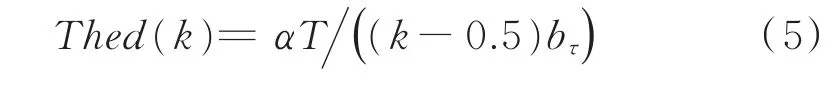
式中，α为门限系数，与脉冲丢失情况和参数测量误差有关，通常α＜1。

PRI变换法可以理解为f(t)的自相关谱函数，变换结果为PRI的谱图，在真实PRI位置会出现峰值，用函数可以表示为：

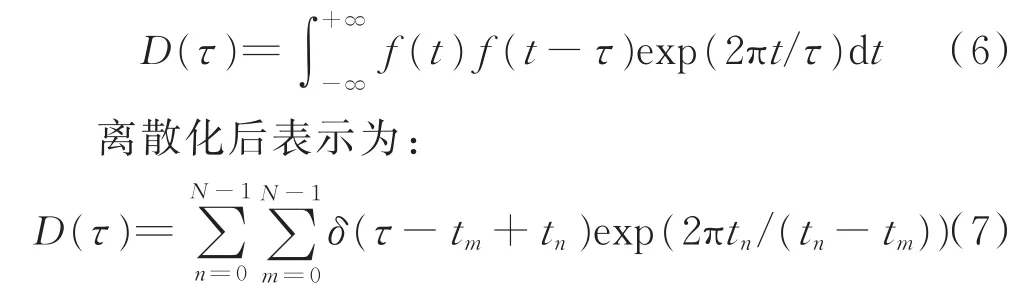
相位因子exp(2πtn/(tn-tm))的引入完全是为了式（2）在计算自相关时产生的谐波。

对于固定重频的PRI，只要保证每个PRI箱的宽度相同即可，对于抖动的PRI，则脉冲会分散到以真实PRI为中心的多个PRI箱内，使得PRI谱变得平坦，因此需要根据PRI值动态调节箱的宽度，即保证箱的宽度必须大于PRI最大抖动范围，根据这一原则，随着PRI中心值增大，箱的宽度也相应增大，得：

式中，ε是决定PRI箱宽度的容差参数，可以根据最大PRI抖动比进行调整。PRI变换门限在文献[6]中进行了详细的分析。

1.3 改进的脉冲分选算法流程

从上述分析可以看出，直方图方法估计适应于固定重频的检测，重频参差可以看作骨架周期为固定重频的信号，适应用直方图方法，对于抖动信号，则需要采用PRI变换的方法进行估计，因此，从算法的通用性上看，PRI变换方法比直方图方法在重频估计上更有优势。但从算法的运算量上看，由于PRI变换采用可变箱的方法，而且存在指数运算，因此运算量上比直方图方法大很多，在工程应用上受到限制。为了保证算法性能的同时降低运算量，本文提出了一种改进的算法，具体流程如图3所示。首先，对输入的高密度PDW进行预处理，大大减少每批目标需要处理的PDW个数；其次，将固定重频（包含参差）信号进行直方图估计，并进行谐波判断，抽取固定目标的PDW；最后，对剩余的PDW进行PRI变换处理，进行抖动分析。由于对目标进行预处理和抽取了大量的固定重频信号，需要PRI变换的PDW数量大大降低，因此在运算量上得到了保证。

图3 改进的脉冲分选算法流程图

2 多DSP并行处理技术

为了提高脉冲分选的处理速度，本文采用多片DSP并行处理的方法提高脉冲分选的速度。目前ADI公司TigerSHARC系列中的TS201是性能最高的浮点数字信号处理器，具有单片运行速度高和专门优化的多的DSP处理器互联设计等突出优点，是信号处理平台的核心处理器。本文采用的是自行研制的通用信号处理平台，采用4片TS201组成，各TS201之间通过LINK口互联。在工程设计是，采用1片TS201完成脉冲描述字的接收，接收完成后进行三维聚类预处理，预处理后的脉冲描述字通过片间LINK口送到其余3片TS201进行脉冲分选处理，处理结束后将形成的雷达描述字通过LINK口送回到第一片进行综合处理，然后将综合的结果送出。本文不采用数据分段并行处理的架构，避免了数据分割后带来的增批，同时也保证了同一批目标的数据的完整性。DSP并行处理的脉冲分选装置框图和信号流图分别如图4、图5所示。

图4 多DSP并行处理的脉冲分选装置框图

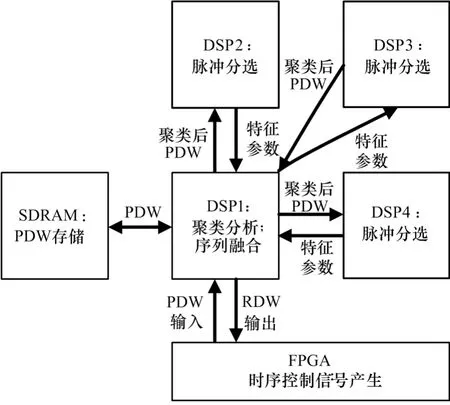
图5 多DSP并行处理的脉冲分选信号流图

3 仿真实验

为了验证算法的有效性，模拟了8批目标，每秒脉冲200万以上，同时为了验证算法的复杂性，同一聚类结果存在多批目标的情况，表1为8批目标参数，根据方位、频率、脉宽聚类出6类，其中第6类包含三批目标，从表1中可以看出，聚类后只需要处理6144个PDW的时序分析就能给出8批目标参数。

表1 模拟8批目标脉冲分选仿真试验

前5类目标为固定重频信号，采用直方图方法可以估计出结果，第6类存在三批目标，时域上相互交错，图6为第6类聚类后到达时间8阶累积差分后的直方图统计和过门限检测结果，从仿真结果上看，直方图方法可以正确估计重频固定和重频参差的PRI值，但存在多阶谐波过门限的情况，因此需要进行过门限谐波判断，同时从图中可以看出，直方图方法不适用于重频抖动PRI的估计。图7为PRI变换方法重频估计和过门限检测情况，从仿真结果可以看出，PRI变换方法具有通用性，可以解决直方图方法不能估计抖动重频的情况，而且没有出现谐波情况。

从脉冲分选效率上看，PRI变换法比直方图方法优势明显，但运行量则大很多。假设脉冲数量为N个，计算M阶差分大约需要的MN次除法运算，而计算PRI变换则需要N的阶乘次指数运算，因此，随着脉冲数N增加，PRI变换运算量成指数增加，无法满足实时运算需求。因此本文在算法上采用直方图统计和PRI变换相结合的方法，尽量减少PRI变换的脉冲个数，同时采用多DSP并行处理的方法提高运算速度。

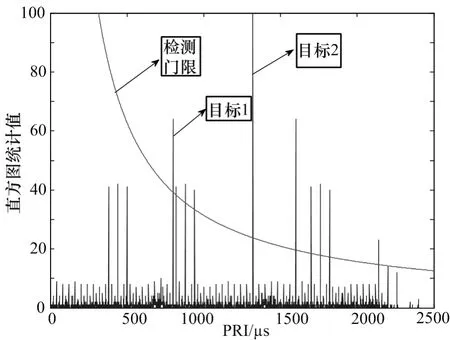
图6 直方图统计法重频估计

图7 PRI变换法重频估计

4 结束语

本文根据高密度环境下脉冲分选的任务要求，从实时信号处理角度出来，努力寻找一种实用的雷达脉冲分选算法。文中首先通过聚类的方法对高密度脉冲描述字进行稀释，然后通过对直方图统计和PRI变换两种重频估计方法进行分析比较，提出一种改进的脉冲分选算法。文章还根据新算法特点，提出了一种用于该算法并行处理的任务分配原则，提供了一种基于4片DSP硬件平台的实时处理方案，从理论分析和仿真的结果看出，本文的方案可以满足高密度环境下实时分选的要求。■