基于三参数威布尔可靠性模型的航空装备故障预测研究

孙扩 赵波 杨航

摘要：针对目前我军装备保障任务维修中存在的设备故障率高和过度检修等问题，以三参数威布尔为基础，基于某飞机历年的故障记录数据，针对该型飞机的几个重要设备开展可靠度建模，并在故障预测中加以验证，与历年同时段同架次飞机故障数据进行对比，验证了该模型和预测方法具有可行性。

关键词：三参数威布尔；可靠度建模；航空设备；故障预测

Keywords：three parameters Weibull；reliability modeling；aviation equipment；failure prediction

0 引言

航空装备维修保障主要有三类：事后维修、定期维修和视情维修[1]。目前，我军装备保障任务维修基本采用的是事后维修与定期维修相结合的方式，该方式虽然有着简单、可操作性强的特点，但是存在设备故障率高和过度检修的风险和挑战。随着设备状态监控技术的兴起，视情维修方式必定成为今后很长一段时间内装备维修保障的发展方向。为此，针对某型飞机的重要电子设备，利用三参数威布尔构建可靠性模型，对设备进行故障预测和实验验证，为该设备的视情维修提供分析依据。

1威布尔分布

威布尔分布[2]因瑞典教授Wallodi Weibull在进行材料强度统计时首次使用而得名，目前已广泛应用于电子元器件寿命试验和机械产品的疲劳寿命试验中。两参数威布尔分布的参数估计简单、适应能力较强，但是某些机电设备特别是航空机电设备，其威布尔概率并非均匀分布，这种情况下三参数威布尔模型更能够描述复杂机电类产品磨损累计失效的分布形式。因此，本文将三参数威布尔模型作为飞机设备可靠性建模的核心模型。

三参数威布尔分布的概率分布函数为：

三参数威布尔分布的失效率函数为：

2 威布尔模型可靠度建模与故障预测

针对航空设备故障开展可靠度建模和故障预测[3]的基本流程如图1所示。

航空设备可靠度建模与故障预测是开展视情维修工作的重点，航空装备可靠性分析本质上是对装备可靠性变化规律的建模，基于可靠性模型，可以实现预先性的装备检修和更换，能够使得装备备件更加具有针对性，从而提升整个地面保障的效率和可靠性。基于可靠性评估结果，可以进行某一种航空装备的总体故障数量（或数量区间）的预测，这种预测结果具有一定的可靠度。

在故障数预测中，由于在要预测的时间区间内各设备的实际使用时间无法准确得到，因此只能通过预测的时间进行估计。为了提高预测的准确度，在计算过程中添加了蒙特卡洛模拟方法[4]。即以预测的时间为样本，通过假设检验方法得到样本服从的分布，再根据分布模型重复生成设备的使用时间的预测序列，在多次计算后取中间值。

2.1 威布尔可靠度建模

在航空设备可靠度建模中，针对某航空设备（如垂直陀螺），依据样本故障数据建立故障发生的概率分布。

这里用到三参数威布尔建模，需要通过故障数据运用MATLAB建模，从而求出三个参数，这是三参数威布尔模型拟合的关键。笔者选择的是利用固定位置参数λ的方法，从而将三参数转化为二参数再进行求解。

具体方法如下：

1）位置参数λ不小于样本故障数据的最小值，所以位置参数在从0到样本故障数据的最小值之间选取。

2）当选择（这个选择相当于猜测）一个位置参数λ后，三参数威布尔分布就变成了一个对应的二参数威布尔分布。

3）用似然法求解尺度参数和形状参数α、β，并且计算出一个似然值。

4）选取一系列的位置参数λ，对于同一个样本故障数据x得到一系列的参数α和β的值以及一系列的似然值。其中，MATLAB库中的算法wblike就是专门针对二参数威布尔分布的，like是通用的，可以用于求解其他函数。

5）如此，在计算出的一系列似然值中选择最大的似然值所对应的一组参数λ、α、β作为样本故障数据x的三参数拟合结果，进而获得可靠度函数和失效率函数。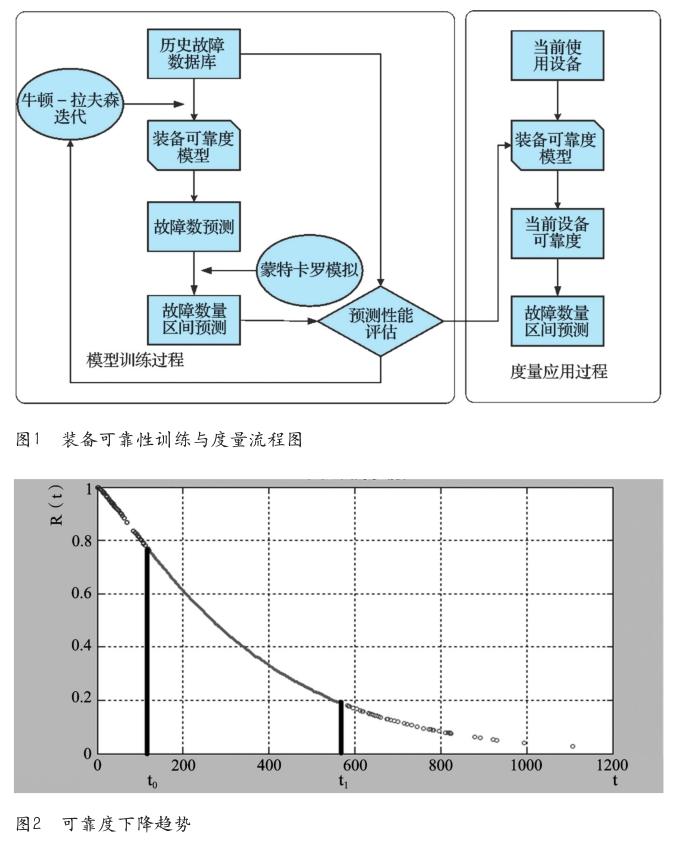

2.2 故障预测

基于以上获得的设备可靠度和失效率信息，开展航空设备故障数量范围的预测，以支撑战备作训备件管理和后勤保障工作。

1）故障数据预测

3 实验验证

3.1 五种设备的建模

下面以垂直陀螺、无线电高度表、涡轮冷却器、防冰大气总温传感器、惯性导航分系统作为参考对象，进行可靠性建模和设备故障预测。

实验数据说明：五种设备的故障数据都是指这五个类型设备装备飞机后到首次发生故障的工作时长。

在航空设备可靠性建模过程中，针对垂直陀螺、无线电高度表、涡轮冷却器、防冰大气总温传感器、惯性导航分系统分别进行三参威布尔模型的估计，通过MATLAB运行得到五种设备分别对应的位置参数、尺度参数和形状参数以及各自的概率密度函数，见图4～图8。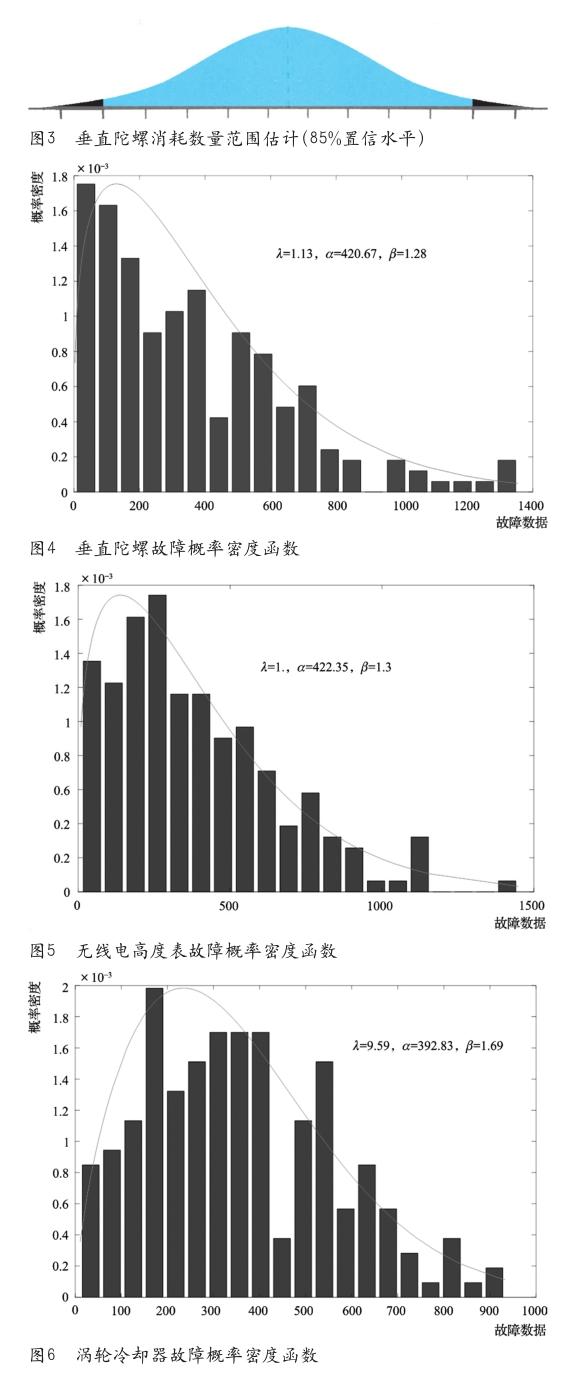

3.2 故障数量区间估计

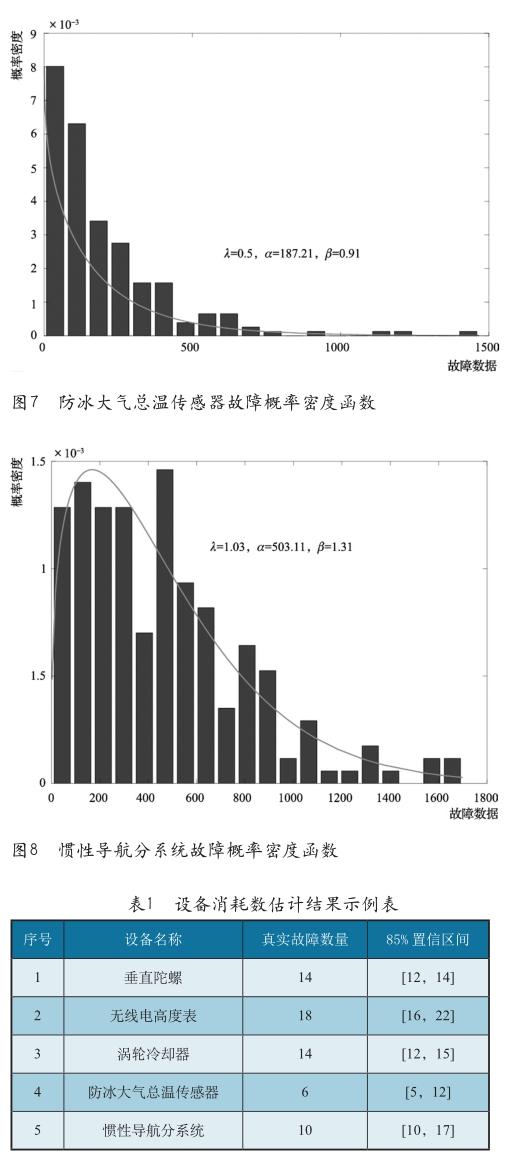
在故障预测过程中，针对垂直陀螺、无线电高度表、涡轮冷却器、防冰大气总温传感器、惯性导航分系统分别进行基于蒙特卡罗模拟的消耗数量区间估计。这里选取85%置信区间，从高斯建模的最高峰即概率最大的那个点向两边扩展，当扩展的面积为总面积的85%时即为选取85%的置信区间，此时临界两点对应的装备故障数即为预测的故障数或故障数区间。最终得到如表1所示的设备消耗数估计结果（其中真实故障数量為已有的数据）。

由表1可以看出：在利用垂直陀螺训练数据建立威布尔模型并求出三个参数的同时进行故障预测后，发现其在85%置信区间内的故障预测数量为12～14个。该架次飞机垂直陀螺在测试数据所在时间范围内的真实故障数量为14。分别对无线电高度表、涡轮冷却器、防冰大气总温传感器、惯性导航分系统进行分析计算，得到了同样的结论。

4结论

综上所述，本文在飞机训练数据的基础上利用威布尔模型求出其三个参数，代入故障预测的公式中，在测试数据的基础上求得的故障预测区间与真实的故障数量基本吻合，真实故障数量在预测的故障区间内，即验证说明了这种预测方法是可行的。

参考文献

[1]林琳，罗斌，钟诗胜. 基于视情维修的机队维修决策方法[J]. 计算机集成制造系统，2019，25（3）：137-148.

[2]姜万民. 关于Weibull分布的加速寿命试验的统计分析[D].昆明：云南大学，2019.

[3]彭宇，刘大同，彭喜元. 故障预测与健康管理技术综述[J]. 电子测量与仪器学报，2010（1）：9-17.

[4]胡峰. 基于蒙特卡洛法的设备可靠性故障预计和分析[J]. 机械工程与自动化，2018（2）：146-148.

作者简介

孙扩，助教，主要研究方向为机载电子设备故障诊断技术。

赵波，高级工程师，主要研究方向为航空通信设备。

杨航，工程师，主要研究方向为航空通信信号处理。