高速铁路轨下基础长期变形预测方法研究
2020-04-11高琨
高 琨
(兰州市轨道交通有限公司,甘肃 兰州 730070)
1 概述
无砟轨道高速铁路一般的运营寿命为100年,规范规定客运专线铁路无砟轨道铺设完成后,最终工后沉降不得大于15 mm,我国普通的有砟轨道沉降要求为:一般路基地段不得大于5 cm、桥涵过渡段不得大于3 cm,在日本,铁路路基最终的工后沉降要求必须不大于10 cm,由此可知若能正确预测出轨下基础长期的变形,对于实际工程具有重大作用。而轨下基础变形主要有路基的不均匀沉降,桥梁的挠曲变形、梁端转角与墩台沉降,以及隧道内可能出现的基岩或抑拱的不均匀沉降变形等[1,2]。路基的不均匀沉降占轨下基础沉降的大部分比例,因此,本文主要针对国内外对路基的不均匀沉降进行综述讨论,长期预测的前提是基于现场实测的路基沉降数据,由此来探讨轨下路基不均匀沉降的变化规律。
2 曲线法
2.1 双曲线法[3,4]
双曲线的计算理论认为路基不均匀沉降以双曲线趋势的速率进行变化,初始计算是从荷载加载完成以后开始,t时刻的沉降量S为:
(1)
(2)
其中,S∞为最终沉降值;S0为加载后的初始沉降;a,b均为所要计算的参数,求解过程为:
将式(1)可变形为:
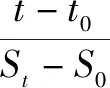
(3)
2.2 三点法[5]
三点法也称为固结度对数配比法,可表示为:
St=Sdαe-βt+S∞(1-αe-βt)
(4)
式(4)有4个未知参数:Sd,α,β,S∞。在前期观测沉降曲线上任意取(t1,S1),(t2,S2),(t3,S3),且要求满足t3-t2=t2-t1。将三个时间点值代入式(4),联立求解就得Sd,β,S∞,其中瞬时沉降值Sd中α=8/π2,相应的求解如下:
(5)
(6)
(7)
2.3 Asaoka法[6-9]
Asaoka求解思路将Mikasa的体积应变固结公式表示为:
(8)
通常取式(8)的一阶方程计算,可得式(9):
(9)
其中,式(9)中的S为求解的未知量,利用Asaoka法求解的最终路基沉降预测为:
S(t)=S∞(1-e-t/α1)+S0
(10)
2.4 星野法[10]
星野利用固结度与时间系数的平方根成正比这一关系,进行了大量的现场试验,得出下列表达式:
(11)
其中,S0为瞬时沉降;A,K均为未知参数;St为t时间的沉降量,式(11)可改写为直线方程形式:
(12)
其中,(AK)-2为直线截距;A-2为直线斜率,假定几组(t0,S0)的值,由实测数据绘制关系曲线(t-t0)(S-S0)-2-(t-t0),求解出最符合线性关系的一条直线,进而求得系数A,K。将系数A与K代入到计算公式中,求得:
群桩基础的承台顶面荷载分布见表3,其中X向为顺桥方向,Y向为平面垂直线路方向,Z向竖直方向。采用不利的重型荷载组合(设备及梁重+离心力+双孔重载+列车横向摇摆力)。
(13)
2.5 Logistic曲线[11]
1938年,Pierre-Francois Verhulst提出Logistic曲线模型,其微分形式为:
(14)
其中,y为沉降量;t为时间;k为瞬时沉降速率;A为最终沉降量,求解得:
(15)
其中,B为待求参数;e为自然常数。
2.6 Gompertz曲线[12-14]
英国统计学家Benjamin Gompertz提出Gompertz曲线模型,其微分形式为:
(16)
其中,y为沉降量;t为时间;k为瞬时沉降速率;A为最终沉降量,求解得:
y=Ae-Be-kt
(17)
其中,B为待求参数;e为自然常数。
3 灰色系统理论法[15-22]
灰度算法又被称为GM(Grey Model)算法,由著名教授邓聚龙提出,主要求解过程为:
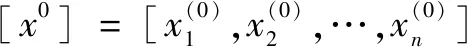
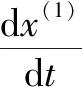
(18)
可得方程结果:
(19)
基于最小二乘原理可得:
(20)
其中:
(21)
(22)
将参数a,b代入式(19),可得:
(23)
4 组合预测模型法[23-25]
组合预测方法有两种组合方式,分别为等权和不等权组合预测模型。
4.1 等权组合预测模型
等权组合预测方法构建方式为设Xi(i=1,2,…,n)为第i个模型的预测值,因而可得全组合中各个单一模型的权系数为1/n,其预测值Xc可通过下式表示:
(24)
4.2 预测误差平方和最小的组合模型
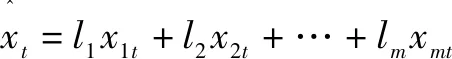
(25)
设J1为预测误差平方和,表达式为:
(26)
由误差平方和最小的原则,其求解就转化为最优问题,如式(27):
(27)

式(27)的矩阵形式可写为:
(28)
模型的最优解和目标函数最优解:
(29)
5 结语
从以上的文献综述中可知,轨下基础长期变形预测方法多种多样,其研究手段由单一模型预测到组合预测模型。发现影响高速铁路软土路基沉降变形的影响因素不仅仅是某一方面,更多的是各个方面因素综合影响,因此在工程建设中采用不同模型进行预测之后,也需要进行现场实地监测,对比两者数据,检验其预测精度。
