基于Janbu模型的路基边坡稳定参数研究★

楼金培 黄益锋 余以强

(浙江省交通运输科学研究院，浙江 杭州 311305)

路基边坡稳定性分析是道路工程中的重要研究课题，它是路基稳定性评价及预报的前提工作，也是进行边坡防护工程设计的重要依据[1]。路基边坡稳定安全系数通常受边坡的内在因素和外在诱导因素的影响，内在因素包括边坡的几何参数坡高H、坡角β、边坡土体力学参数容重γ、粘聚力c、内摩擦角φ和孔隙水压力r等，外在诱导因素包括车辆震动、地震、降雨和地下水位升降作用等[2]。

对于边坡的稳定性分析，重点的研究方向集中在路基边坡失稳模型、路基边坡分析技术和软件以及路基边坡失稳的影响因素。徐云哲[3]采用有限元对粉砂土路基边坡稳定性进行了分析，并提出三维植被固土网格能有效防止路基边坡失稳；王红星[4]归纳分析了影响高填路基边坡稳定性的各种因素，研究了泥岩边坡在考虑降雨条件下的稳定性规律及稳定性安全系数，对其变形破坏机理进行了分析研究;刘源[5]结合典型工程实例采用Bishop法和有限元强度折减法分别进行计算，探讨有效的防治山区高速公路挖方边坡失稳滑坡的方案；蒋鑫等[6]基于剪切强度折减法,就影响填砂路基边坡稳定性的各设计参数进行敏感性分析,提出增强填砂路基边坡稳定性措施,为高速公路建设提供依据。

实际工程中，路基边坡的安全系数是预期设计的，而根据理论模型反推土体三个力学参数γ,c,φ的相关报道较少。本文采用Janbu法不仅考虑了土体的重力，还考虑了动荷载、内部的粘聚力，运用Matlab编程分别反推出土体三个力学参数γ,c,φ。对实际的路基边坡设计具有一定的参考价值。

1 建立路基边坡稳定性计算模型

1.1 边坡稳定性常用计算方法介绍

常用边坡稳定性系数的计算分析方法有，Bishop法、Janbu法和Morgenstern-Price法(简称M-P法)。但这三种方法各有缺点，Bishop法仅考虑边坡土体的质量，计算的结果偏小；Janbu法不仅考虑了土体的重力，还考虑了动荷载、内部的粘聚力，因此，计算的结果比较准确；Morgenstern-Price法(简称M-P法)计算的结果偏大，并且计算过程比较复杂。

1.2 建立Janbu模型

按照1.1的分析，本文用Janbu法建立边坡稳定性模型，建模过程如下。

如图1所示，作用的集中荷载包括ΔP，ΔQ及均布荷载q，ΔWγ为条块自重，在条块两侧作用有条间力T，E及T+ΔT,E+ΔE，ΔS及ΔN为滑动面上的作用力。通常，T，E，ΔS及ΔN为基本未知量。然后建立力学分析模型见图2。

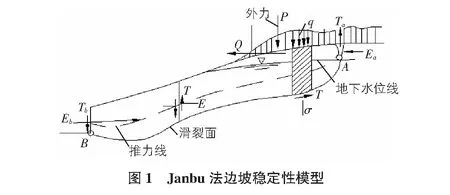
Janbu法的安全系数通过式(1)，式(2)确定：

(1)

(2)

2 模型求解

通过Janbu法建立边坡稳定系数模型，然后，用原始的数据进行模型验证，检验模型的准确性，最后用MATLAB进行编程反解，在安全系数已知的情况下，求解重度、粘聚力和内摩擦角三个土力学参数中一个未知的参数值。反解过后，对反解的参数值，与原始数据进行比较，验证反解的准确性。

2.1 Janbu法建立边坡稳定安全系数模型验证

首先，选取普通路基边坡和高水位路基边坡各9组原始数据，代入模型，求解安全系数。安全系数求解结果分别如表1，表2所示。

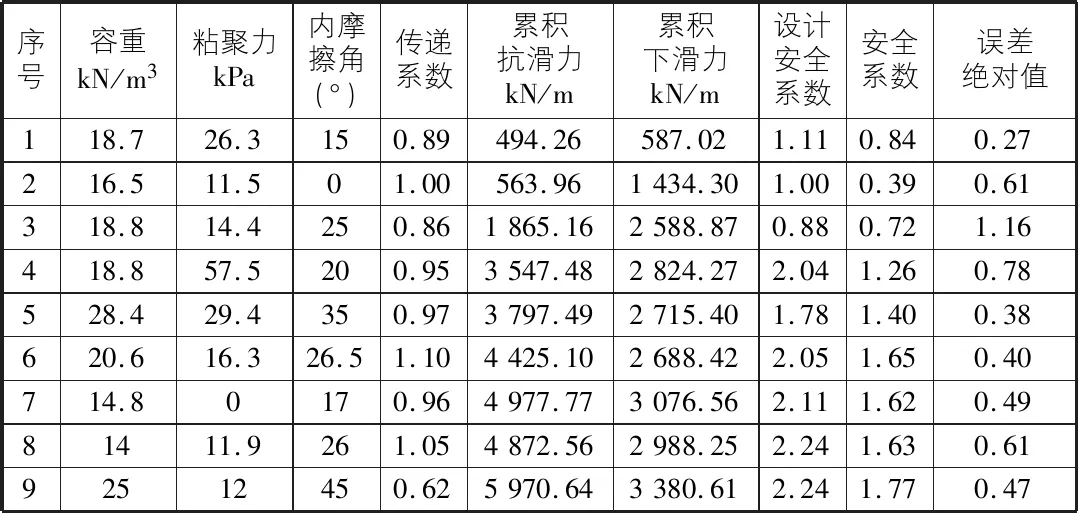
表1 Janbu法普通路基边坡安全系数计算

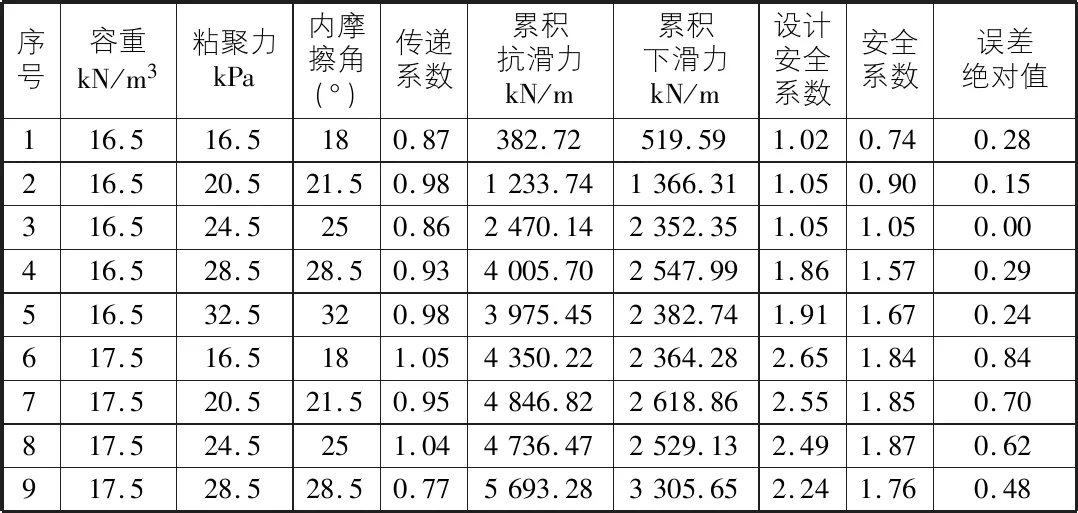
表2 Janbu高水位路基边坡安全系数计算

从表1，表2的计算结果看，Janbu法计算的安全系数与原数据安全系数的绝对值误差较小，最大的误差为0.84。因此，模型计算结果较准确。

2.2 边坡安全系数反解

为充分显示模型的计算能力和准确性，对普通路基边坡和高水位路基边坡的三个力学参数γ,c,φ，按照缺一个参数进行反解，得出3组反解值，分别与原参数数据进行比较。普通路基边坡参数反解见表3，表4，高水位路基边坡参数反解如表5,表6所示。

表3 普通边坡反解土体容重参数及粘聚力参数

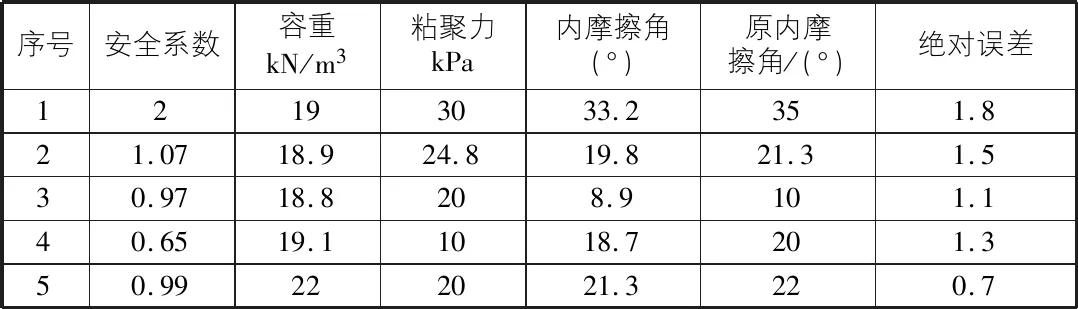
表4 普通边坡反解土体内摩擦角参数

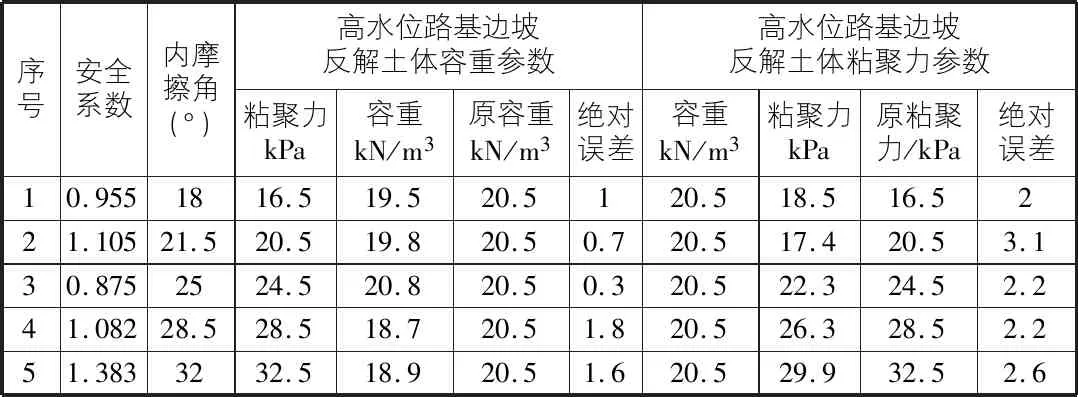
表5 高水位路基边坡反解土体容重参数及粘聚力参数

表6 高水位路基边坡反解土体内摩擦角参数

2.3 参数反解结果分析

在普通路基边坡中，误差绝对值最小值出现在土体容重参数的反解中，绝对误差值为0.3(1.46%)；误差绝对值最大值出现在土体内摩擦角参数的反解中，绝对误差值为1.8(5.42%)。

相对于普通边坡，高水位路基边坡的参数反解值误差则相对较大。其中，高水位路基边坡误差绝对值最小值出现在土体容重参数的反解中，绝对误差值为0.3(1.58%)；误差绝对值最大值出现在土体内摩擦角参数的反解中，绝对误差值为2.7(9.47%)。

由此可见，采用Janbu法建立的边坡稳定性系数模型，在求解安全系数时具有很好的可靠度，并且在反解土体容重和粘聚力方面误差较小，但在反解土体的粘聚力参数时，误差较大。并且总体上高水位路基边坡的参数反解误差要大于普通路基边坡。

3 结语

1)Janbu法计算出来的安全系数与原始的数据安全系数的绝对值误差较小，最大的误差为0.84，模型计算的结果较为准确。

2)采用Janbu法建立的边坡稳定性系数模型反解土体容重和粘聚力方面误差较小，但在反解土体的粘聚力参数时，误差较大。

3)相对于普通边坡，高水位路基边坡的参数反解值误差则相对较大，普通路基边坡中，误差绝对值最大值出现在土体内摩擦角参数的反解中，绝对误差值为1.8(5.42%)，而水位路基边坡的土体内摩擦角参数的反解误差为2.7(9.47%)。