崩积层纵坡向双桩承载力影响因素分析

石 斌 马福民 蒋一波 孙军柱 雷俊锋 温树鑫

(1.中电建路桥集团有限公司，北京 100048； 2.中国水电建设集团十五工程局有限公司，陕西 西安 710065)

0 引言

陡坡常常由于巨大的岩体、土体、块石和碎屑物突然发生急剧的崩落、滚落或翻转而造成严重的灾害，是道路中的事故多发路段,因此陡坡崩积层纵坡向双桩的承载力的好坏是陡坡路段安全与否的决定性因素。

国内的学者目前已经对这方面的工程问题做了一系列研究，并且也有了进展。赵明华[1]提出适用于高陡边坡桥梁基桩的桩后岩质边坡滑坡坡体推力计算模型和内力及位移分析的有限差分解。杨明辉[2]提出对山区高陡边坡桥梁基桩荷载进行合理简化，滑动面以下地基比例系数k服从线性增长规律并且计入桩顶p—Δ效应的影响。蒋鹏飞等[3]认为当嵌岩达到一定深度后，增加嵌岩深度对提高承载力作用不大，应取2倍～3倍桩径。罗卫华等[4]建立了岩质边坡桥梁双排基桩三维有限元计算模型，降低了对桩身材料强度的要求。严飞淞等[5]分析了在施工荷载作用下桥梁桩基和陡坡本体的位移分布和变化规律。余继东和马炽藩[6]指出了临界施工荷载对控制桥梁桩基稳定性的重要意义。

目前我们研究桩基承载力影响因素已取得较大的突破，但是仍不够全面，本文将以马边河2号桥沐川岸左线为研究对象，从当地的气候、水文条件、地形、地质条件等各方面着手调查，分析影响陡坡崩积层纵向桩基承载力的因素。

1 竖向位移的控制微分方程求解

假设桩侧阻力的分布[7]如下：

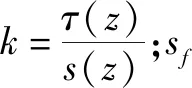
假设桩端阻力按照三折线函数分布[8]：

其中，kb1,kb2为沉渣与岩土体的端阻传递系数；ξ0,ξf分别为桩端弹性压缩阶段的初始位移与结束点的位移；qpf为端阻极限值。

根据桩基的传递函数控制微分方程，即：

代入相关函数，可求得按桩顶沉降控制的嵌岩桩的控制微分方程为：

根据相关初始边界条件和连续性条件，以及基于现场资料，查得桩基的刚度EA以及各项参数，即可求解出桩顶极限荷载的具体值。

2 纵坡向双桩的竖向极限荷载影响因素分析

从桩顶极限荷载的计算公式不难看出，影响桩基承载力的因素主要有6个。为进一步探讨桩基在桩侧摩阻力与桩端阻力弹性未进入塑性阶段时桩基的承载力特性，下面将以一实际工程为依托，基于现场数据重点分析影响桩基承载力的主要因素。

2.1 依托工程整体介绍

G4216线仁寿经沐川至屏山新市(含马边支线)段高速公路(以下简称仁沐新高速公路)马边支线段路线起于仁寿经沐川至屏山新市镇高速公路主线新凡乡附近，与主线沐川枢纽相接，止于马边县城北侧红牌坊大桥附近，全长43.847 km。其中桥梁1 332 m/3座，马边河1号大桥左线772 m，右线772 m；罗汉溪中桥左线40 m，右线40 m；马边河2号大桥左线525 m，右线514 m。本文取马边河2号桥沐川岸左线陡坡上的嵌岩桩作为研究对象，对该桩基按桩顶沉降量控制进行竖向承载力计算。

2.2 按桩顶沉降量控制的桩基竖向承载力

根据设计和施工等单位提供的资料可知：桩基的弹性模量E=30 GPa，桩长l=17 m，桩径为2 m。桩侧摩阻力的传递系数k=600 kPa/mm，在考虑沉渣的影响时，桩侧摩阻力到达极限值时桩端位移ξ0=s0=1 mm，桩端阻力的传递系数k1=80 kPa/mm,k2=800 kPa/mm，桩端阻力到达极限时桩端位移ξf=sf=1.8 mm。

2.3 单因素分析

选取桩基的直径d、桩长l、桩基的弹性模量E、桩侧摩阻力的传递系数k、桩端阻力的传递系数k1,k2这6个参数作为研究对象，分别对每一参数增加10%,20%,30%,40%,50%，计算竖向极限荷载的增长率，其计算结果如表1～表6所示。

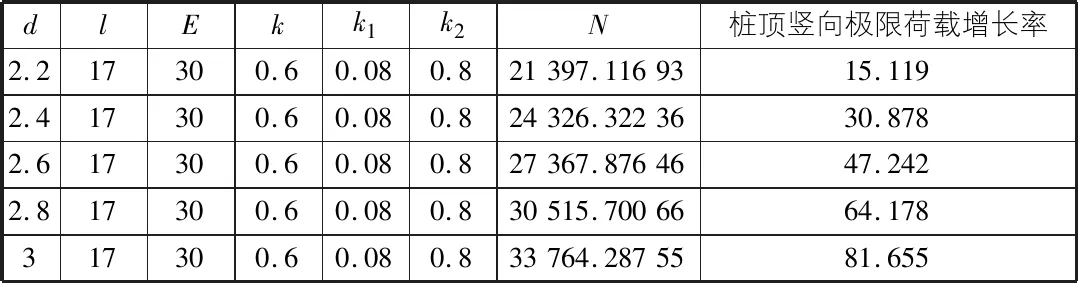
表1 桩径对桩顶竖向极限荷载的影响程度计算表

由表1可知，桩径对桩基竖向极限荷载的影响程度较大，呈递增趋势，说明桩径是影响承载力的主要因素之一。因此，在桩基承载力不足时，可以适当增大桩基，但也需要考虑经济性的问题。

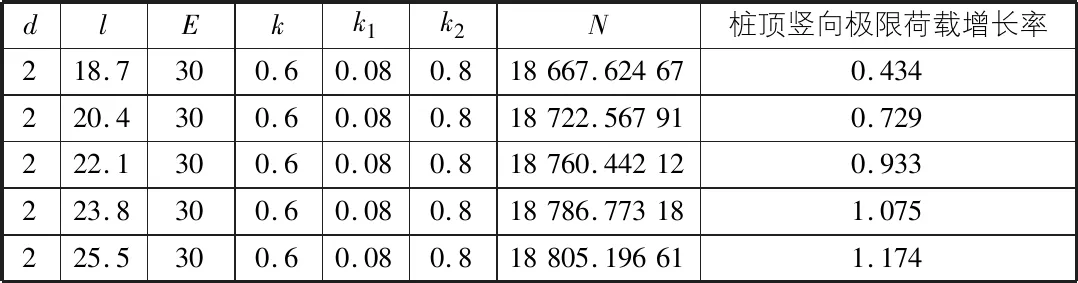
表2 桩长对桩顶竖向极限荷载的影响程度计算表

由表2可知，增大桩长对桩基承载力的影响不大。这是因为假设桩侧摩阻力处于弹性阶段，所以桩侧摩阻力未完全发挥，那么此时增加桩长自然就不会提高桩基承载力。但也可知道，桩侧摩阻力处于弹性阶段时，桩长是影响桩基承载力的次要因素。

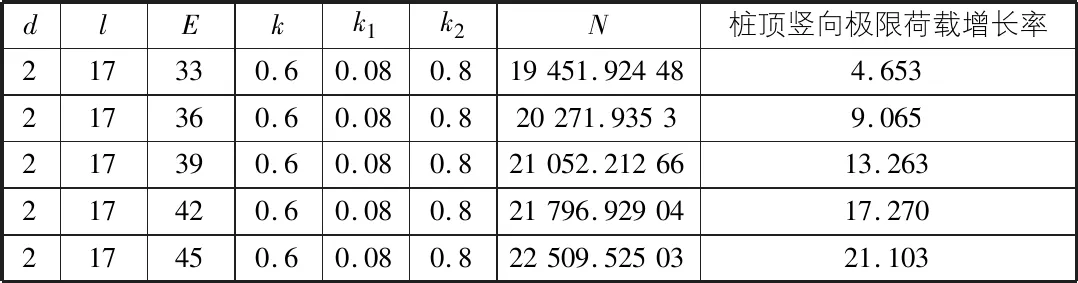
表3 弹性模量对极限荷载的影响程度计算表

由表3可知，桩基的弹性模量对竖向极限荷载的影响较大，但比桩径的影响小。在增强桩基承载力时，应根据实际条件选择增大桩径和选用弹性模量较大的材料。

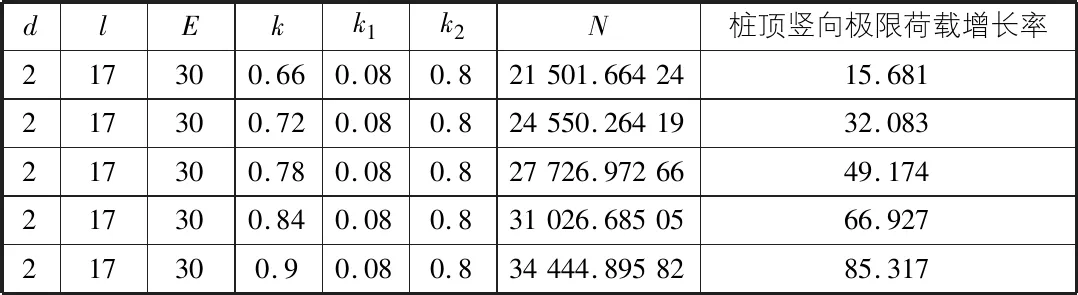
表4 桩侧摩阻力的比例系数对极限荷载的影响程度计算表

由表4可知，桩侧摩阻力的比例系数对极限荷载的影响很大，与桩径的影响几乎相当，略大一点。这说明在桩侧摩阻力处于弹性阶段时，桩侧岩土体的类型对桩顶竖向极限荷载的影响程度很大。岩土体越密实，那么摩阻力就越大，桩基的承载力也就越高。

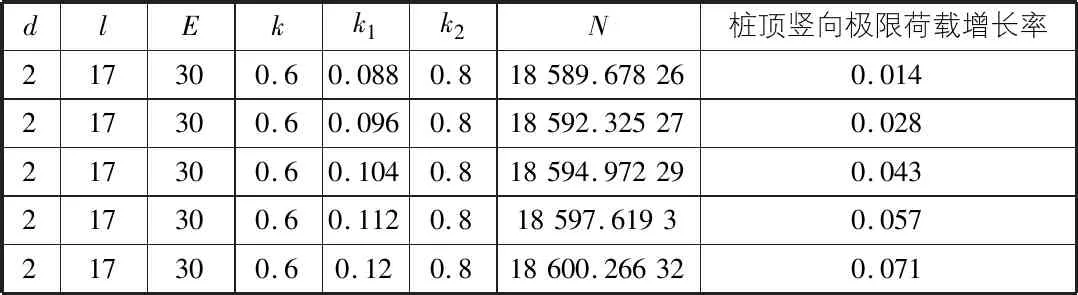
表5 桩端阻力第一阶段的比例系数对极限荷载的影响程度计算表

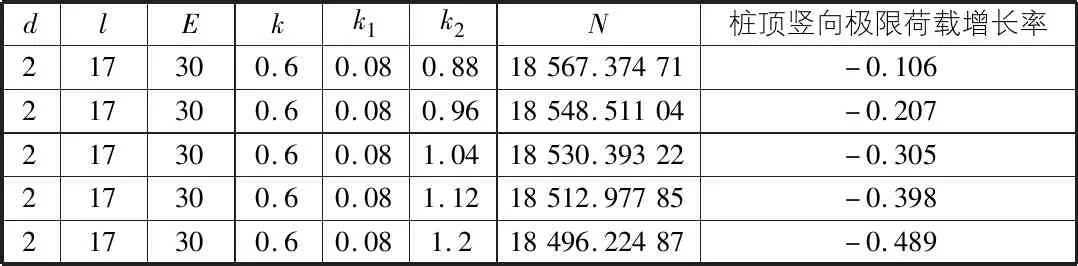
表6 桩端阻力第二阶段的比例系数对极限荷载的影响程度计算表

由表5，表6可知，当桩侧摩阻力处于弹性阶段时，桩端阻力也处于弹性阶段，但也是未发挥的阶段，其第一、第二阶段的比例系数对承载力的贡献都不大，甚至第二阶段的比例系数对桩基承载力有些许减小的趋势。

综上可知，桩侧摩阻力的比例系数对桩基的承载力影响最大，其次是桩径，再是弹性模量与桩长，而桩端阻力的比例系数对桩基承载力的影响几乎没有。但是在实际工程中，仅有桩径和弹性模量是可控因素，而桩侧摩阻力则是岩土体固有的性质，无法轻易改变。所以，为了提高桩基的承载力，应该多从弹性模量与桩径入手。不过，无论是增大桩径还是改用弹性模量高的材料，都会增大造价，工程中应根据实际情况选择最优方案，保证安全性和经济性。

3 结语

本文推导了按桩顶沉降控制的嵌岩桩的控制微分方程，并建立了桩侧岩土体处于弹性阶段时桩顶极限荷载的求解方法，获取了影响桩顶极限荷载的因素主要有6个：桩基的直径、桩长、弹性模量、桩侧摩阻力的传递系数、双桩桩端阻力的传递系数。最后以四川仁沐新高速公路马边河2号桥沐川岸左线陡坡上的嵌岩桩作为研究对象，对影响该桩基的竖向极限荷载的各因素进行了分析。结果表明在桩侧摩阻力处于弹性阶段时，桩侧摩阻力的比例系数、桩径和桩基的弹性模量是影响桩基承载力的主要因素，而桩长和桩端阻力的比例系数则是次要因素。

在实际工程中，仅有弹性模量是可控因素，而桩侧摩阻力则是岩土体固有的性质，无法轻易改变。所以，为了提高桩基的承载力，应该多从弹性模量入手。不过，这意味着会增大造价，工程中应根据实际情况选择最优方案，保证安全性和经济性。