考虑卯口缺陷的直榫节点转动刚度理论分析

刘继远 吴秀峰 李龙飞 张桐瑞 段永旭 申晓广

(辽宁工程技术大学土木工程学院，辽宁 阜新 123000)

0 引言

木结构是历史留给我们的重要财富。穿斗式木结构建造方便，构造简单，抗震性能好。半刚性的节点转动是以木材的变形为代价的，而且也能够承受弯矩，所以能逐渐耗散地震能量。目前研究热点是半透榫节点和燕尾榫节点，在文献[1]中对燕尾榫节点进行了研究，得出横纹受压区对抵抗弯矩的贡献最大。在文献[2]中，对半透榫节点做了研究，推导出了理论模型，并给出了三折线力学模型。

为将同类节点的弯矩—转角关系公式和转动刚度理论公式应用到各种有限元软件中提供可能和理论依据，方便实际维修加固榫卯节点的工程应用，本文将在考虑卯口缺陷的基础上推导出转动刚度理论公式。

1 基本假定

本文在对节点转动刚度进行理论分析时，采用以下假定：

1)节点认为是刚性节点，受压变形只考虑榫头与卯口挤压处；

2)不考虑柱的变形；

3)直榫节点的抵抗弯矩中不考虑榫头与卯口的侧面摩擦力的贡献，认为抵抗弯矩只由榫头上、下受压区应力以及与之有关的摩擦力提供；

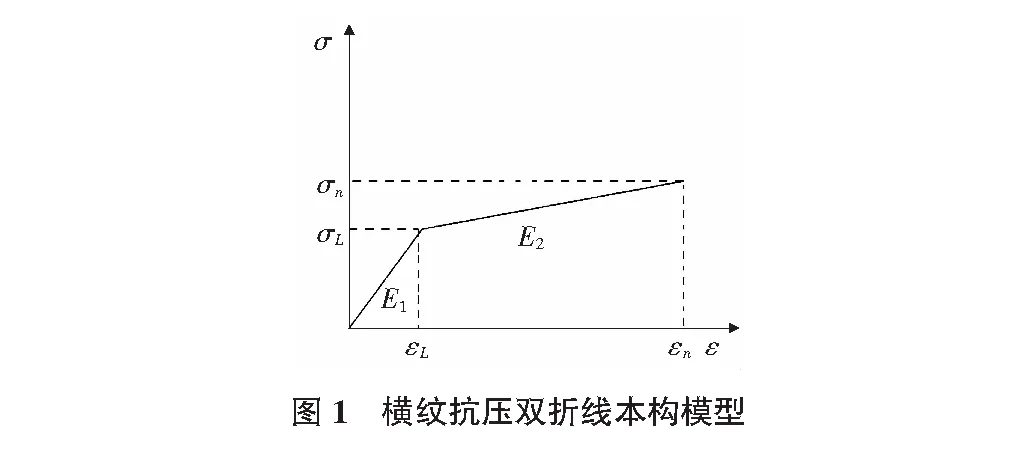
4)枋的应力—应变关系采用横纹受压双折线本构模型，如图1所示，其中横纹受压线弹性阶段的弹性模量E1与横纹受压屈服阶段切线模量E2的值，视具体木材种类而定。

2 节点转动刚度理论推导

在对穿斗式木结构直榫节点进行低周往复荷载时，每一次循环都要经历正向、反向的加载、卸载。弄清这四个阶段中节点的受力与变形状态是研究节点理论模型的前提。在穿斗式木结构中，节点是由枋直接穿过柱子形成的，本文研究的节点中枋属于挑枋，而且枋的截面没有进行削弱，所以在每次循环所经历的四个阶段中，边节点的变形与应力分布情况一致。

本文所说的卯口缺陷是指榫头与卯口之间有初始缝隙。对于有初始缝隙的节点来说，对其进行正向加载、卸载时，在初始转角范围内节点以卯口左下角点为转动中心进行旋转，即节点绕如图2中所示的C点转动；当转动角度大于初始转角时，如图3所示，此时节点转角已不再是卯口左下角点，而是图3所示的C点，随着加载、卸载，C点的位置一直在变化，但始终位于图3中O点的左侧。

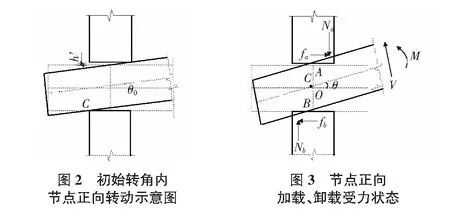
对于无初始缝隙的节点来说，对其进行正向加载、卸载时节点的转动中心从加载开始到卸载结束一直在变化，同样也始终位于图3中O点的左侧。在对节点进行反向加载、卸载时，枋的转动中心点C也一直位于点O的左侧。

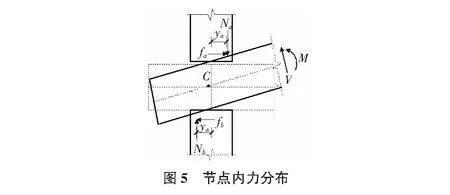
对于直榫边节点来说，因为有右端剪力的存在，所以在正向加载、卸载时都有Na>Nb。Na为榫卯节点上受压区内压力的合力，Nb为榫卯节点下受压区内压力的合力，fa为榫卯节点上受压区内的摩擦力，fb为榫卯节点下受压区内的摩擦力，AB为柱子的中轴线，平衡位置枋中线与柱子中轴线AB的交点为O点。

2.1 几何条件

2.2 应力与变形关系

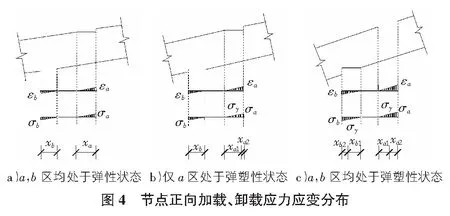
根据横纹受压双折线本构模型计算节点应变，可得每个受压区在两种状态下的应力公式，进而可以推出每个受压区产生的压力和弯矩。如图4所示,εa为节点枋上受压区a的最大应变，εb为节点枋下受压区b的最大应变，σa为节点枋上受压区a所对应的最大应力，σb为节点枋下受压区b所对应的最大应力，σy为节点枋受压区在弹性阶段时对应的最大应力，xa1为节点枋上受压区a处于弹塑性阶段时其中弹性阶段所对应的受压区长度，xa2为节点枋上受压区a处于弹塑性阶段时其中塑性阶段所对应的受压区长度，xb1为节点枋下受压区b处于弹塑性阶段时其中弹性阶段所对应的受压区长度，xb2为节点枋下受压区b处于弹塑性阶段时其中塑性阶段所对应的受压区长度。

2.3 内力平衡条件

如图5所示，节点依靠枋受压区的压力和与附加产生的摩擦力来提供抵抗弯矩。

依据力的平衡条件可得：

加载过程中:

M=Naya+Nbyb+

卸载过程中:

M=Naya+Nbyb-

2.4 节点转动刚度理论公式

依据受压区在弹性阶段的变形与受力状态和弹塑性阶段的变形与受力状态，分别推出两个阶段的节点转动刚度理论公式。

加载过程中:

(1)

卸载过程中:

(2)

因为节点转动中心C是一直变化的，所以xa可以看作是关于转角θ的函数，可根据力的平衡条件按以下公式计算：

(3)

式(3)中Na,Nb,M都是标量，始终取正值；当计算处于正向加载与卸载时，等式右边采用正号；当计算处于反向加载与卸载时，等式右边采用负号；l表示枋上加载点与节点中心之间的水平距离。

式(3)可整理为:

(4)

由式(4)可以得到xa关于θ的函数：

xa=j(θ)

(5)

将式(5)代入到式(1)、式(2)中可以得出节点转动刚度理论公式。

3 残余变形的影响

当到达弹塑性阶段后，节点的塑性变形将占主导且变形不可恢复，继续加载，则塑性变形会持续增长，榫头与卯口之间的缝隙也逐渐增大，节点的刚度变小。在进入塑性阶段的受压区域中，不同位置的塑性变形大小是不一样的，为了简化计算，将进入塑性阶段的受压区域的塑性变形视为相同的，都按平均塑性变形考虑。因此，节点受压区a,b的平均塑性变形分别可以用以下两个公式表示：

将节点受压区a,b的塑性变形计入初始缝隙h′，即可在模型中考虑残余变形的影响，表达式如下：

由于在加载过程中节点受压区a,b存在残余变形，导致每次循环所产生的残余变形会对下一次的循环产生影响，所以每次循环结束后，需要计算出节点受压区a,b的残余变形，将其代入到初始缝隙h′中，当成下次循环计算时的已知量。

4 结语

本文从穿斗式木结构榫卯边节点变形特点入手，考虑榫头与卯口之间初始缝隙的影响，从理论层面推导了榫卯边节点受压区的内力平衡条件和应力、应变公式，进而得到考虑卯口缺陷的直榫节点转动刚度理论公式，为将同类节点的弯矩—转角关系公式和转动刚度理论公式应用到各种有限元软件中提供了可能。