三种边界条件下箱型梁剪力滞效应的解析公式★

周月娥

(广西民族大学建筑工程学院，广西 南宁 530006)

0 引言

箱型梁在对称荷载作用下的弯曲存在剪力滞现象效应。在该效应影响下,箱梁沿着翼板的弯曲应力呈曲线分布,因此不能仅仅依靠初等梁理论来解决问题。对于剪力滞效应的研究，三种常用的方法得到了研究和发展：解析理论[1]、数值解法[2]和模型试验[3]。能量变分法是一种用的比较广泛的解析理论方法。本文考虑外荷载作用为集中力，以附加挠度为基础建立箱梁的纵向位移函数和总势能泛函[4]，推导出三种不同边界条件下箱梁附加挠度的一般表达式。结合欧拉梁挠度，可以得到箱梁挠度和应力的表达式。在此基础上，进一步推导了剪力滞系数的表达式。

1 不同边界条件下箱梁的附加挠度

文献[4]给出了在集中力作用下的箱梁附加挠度及其1阶～3阶导数的表达式，现结合不同边界条件给出箱梁具体的附加挠度表达式:

1)两端简支箱梁。

wa(x)的四个边界条件为：

(1)

另外结合从变分条件出发要求[5]在集中力作用点位置x=ξ处的边界条件有:

当x<ξ时，

(2)

当x≥ξ时，

(3)

2)两端固定箱梁。

wa(x)的四个边界条件为：

(4)

另外结合从变分条件出发要求[5]在集中力作用点位置x=ξ处的边界条件有:

当x<ξ时，

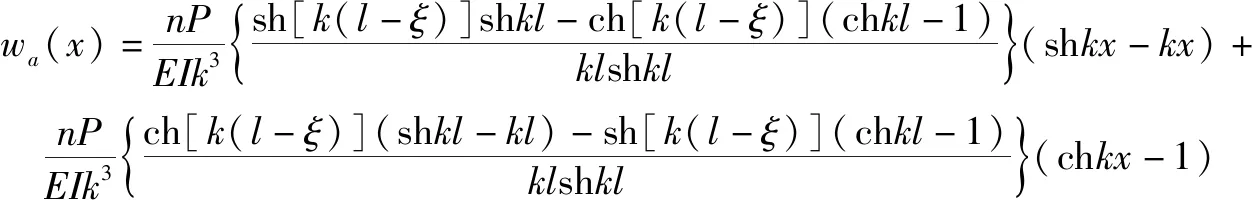
(5)

当x≥ξ时，

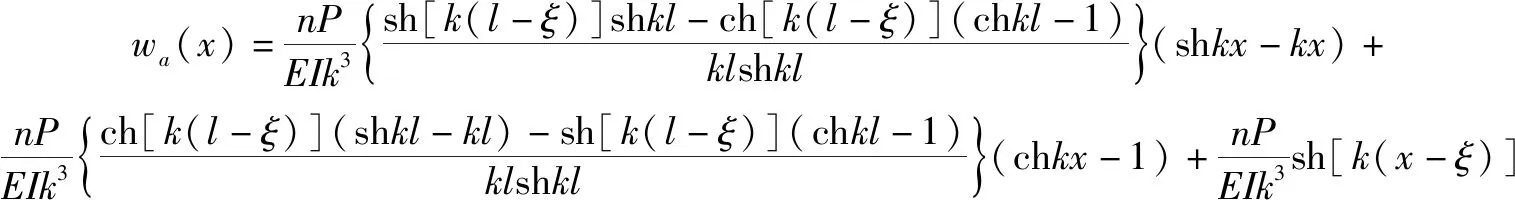
(6)

3)左固右简箱梁。

wa(x)的四个边界条件为：

(7)

另外结合从变分条件出发要求[5]在集中力作用点位置x=ξ处的边界条件有:

当x<ξ时，

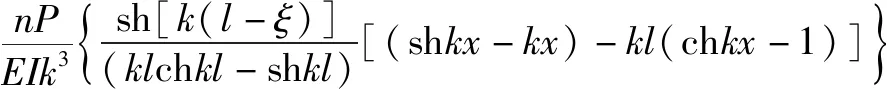
(8)

当x≥ξ时，

(9)

2 不同边界条件下箱梁的挠度

根据Euler梁理论可以单独确定经典梁挠度wc(x)，然后确定箱梁挠度w(x)=wc(x)+wa(x):

1)两端简支箱梁。

当x<ξ时，

(10)

当x≥ξ时，

(11)

2)两端固定箱梁。

当x<ξ时，

(12)

当x≥ξ时，

(13)

3)左固右简箱梁。

当x<ξ时，

(14)

当x≥ξ时，

(15)

3 不同边界条件下箱梁的应力

确定了不同边界条件下Euler梁挠度wc(x)和附加挠度wa(x)后，可以由下式求出箱梁的应力:

(16)

4 不同边界条件下箱梁的剪力滞系数

由挠度和附加挠度定义的剪力滞系数来求解不同边界条件下的具体表达式是：

1)两端简支箱梁。

当x<ξ时，

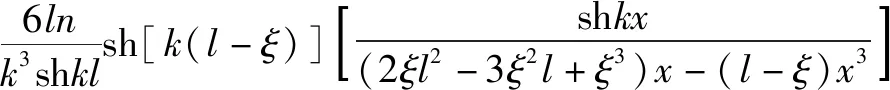
(17)

左端简支端:

(18)

当x≥ξ时，

(19)

右端简支端:

(20)

2)两端固定箱梁。

当x<ξ时，

(21)

左端固定端:

(22)

当x≥ξ时，

(23)

右端固定端:

(24)

3)左固右简箱梁。

当x<ξ时,

(25)

左端固定端:

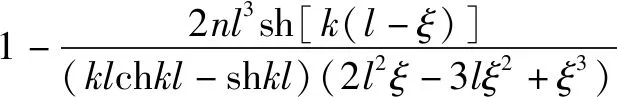
(26)

当x≥ξ时,

(27)

右端简支端:

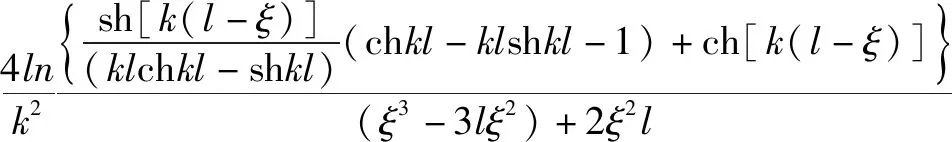
(28)

5 结语

本文利用基于附加挠度得到的一般表达式推导得到了两端简支梁、两端固定梁和左端固定右端简支三种边界条件下箱梁的附加挠度，推导了三种边界条件下箱梁的Euler梁挠度，在此基础上可以得到箱梁挠度和应力的解析表达式。利用基于挠度和附加挠度定义剪力滞系数的公式可以得到三种边界条件下反应剪力滞效应的剪力滞系数公式。