基于非结构化网格的含蜡原油管道周围土壤温度场模拟

戚菁菁，初同龙，孙伶

1.中国石油天然气管道工程有限公司（河北 廊坊 065000）

2.中石油管道局工程有限公司 燃气分公司（河北廊坊 065000）

3.中国石油管道分公司 科技处（河北 廊坊 065000）

0 引言

我国所产原油80%以上为高含蜡、高凝点、高黏度的蜡基质原油[1]。对于易凝高黏的含蜡原油，由于管道周边为自然温度场，环境温度相对较低，因此若管道在常温下运行容易因沿线温降过快导致沿程摩阻急剧升高而被迫停输，甚至可能发生凝管事故。由于管道温度场的变化会显著影响热油管道的最小输量及安全运行[2]，因此准确模拟出含蜡原油管道周围温度场分布至关重要。

在计算管道内油流温度场时，常选用一维、二维或三维温度场计算。管线结蜡层、管壁、防腐层及土壤之间传热在物理上是复杂的三维问题，然而轴向温度梯度相对径向温度梯度非常小，因此工程上可以忽略轴向温降影响，这样三维导热问题就简化为二维土壤温度场模拟问题。文献[3]将土壤温度场假设为一维分布即温度变化只发生在纵向上，由于这种方法过于简单，计算结果同实际测量的结果相比有非常大的误差，因此工程上不予使用。

对于一维、二维和三维温度场，其计算方法通常包括解析法、实验方法以及数值计算等[1-3]。解析法按Fourier 的热传导方程进行求解，能够获得问题的精确解，并且可以为数值计算和实验法提供比较依据。但是该方法存在很大的局限性，即使求解简单的导热问题也相当复杂，对于复杂几何形状的物体和非线性边界条件下的导热问题，应用解析法几乎是不可能的。实验方法是传热学的基本求解方法，通过实验可以得出相对准确的结果，但是此种方法的适应性不好，针对某个特定的问题总是要进行新的实验，耗费的人力、物力和财力巨大，并且实验周期长。数值计算在很大程度上弥补了解析法和实验方法的缺点，其适应性强，特别是对于复杂问题更显其优越性[2-4]。

针对非网格划分对不规则区域具有良好适应性及容易实现网格自动化生成等特点[5-6]，本文采用拉普拉斯变换将土壤的半无限大区域转换为有限矩形区域，考虑到土壤的物性变化，采用基于非结构化网格离散管线周围的土壤温度场。

该类型网格常用的基本单元是三角形和四面体，生成方法包括规则划分法、Delaunay 三角剖分法以及阵面推进法等[5-6]。对二维而言，三角形网格可以充满任意几何形状的区域。虽然其生成过程较为繁琐，数据结构相对复杂，但具有自适应的优点。因此选用二维非结构化网格的数值计算方法模拟计算冻土区含蜡原油管道温度场。

1 数学模型

埋地管道正常运行过程中，传热过程包含3 部分，分别为管内油流以热对流方式传热至结蜡层，再通过结蜡层、管壁、防腐层等将热量交换至周围土壤，最后经地面与大气换热。内部因素和外界环境因素共同构成了影响热油管道散热的影响因素。其中内部因素有油品热物理性质、管道输量、管径以及结蜡层、管壁、防腐层等。外界因素有埋地管段土壤物性、大气温度、风速等。其物理结构模型如图1、图2所示。

根据简化，基于图1、图2，综合考虑界面上各层之间的相互影响，建立热油管道正常运行过程水力-热力模型。

1.1 流体方程

质量守恒方程：

式中：ρ 为密度，kg/m3；A 为管流截面面积，mm2；V 为流体平均速度，m/s；τ为时间，s；z为管道轴向位置，m。

图1 埋地管道剖面

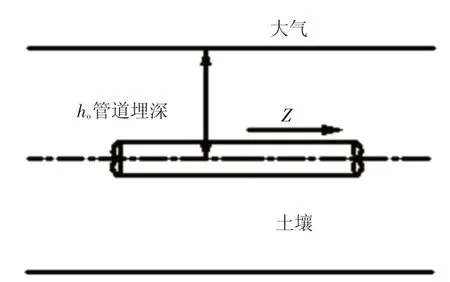
图2 埋地管道示意图

动量守恒方程：

式中：α 为管道轴向与水平方向的夹角，（°）；g 为重力加速度，m/s2；p 为油流截面平均压力，MPa；f 为摩阻系数；D为管道内直径，mm。

考虑到油流的速度方向，V2应该改为V|V|，不失一般性，本文中予以简化。

能量方程：

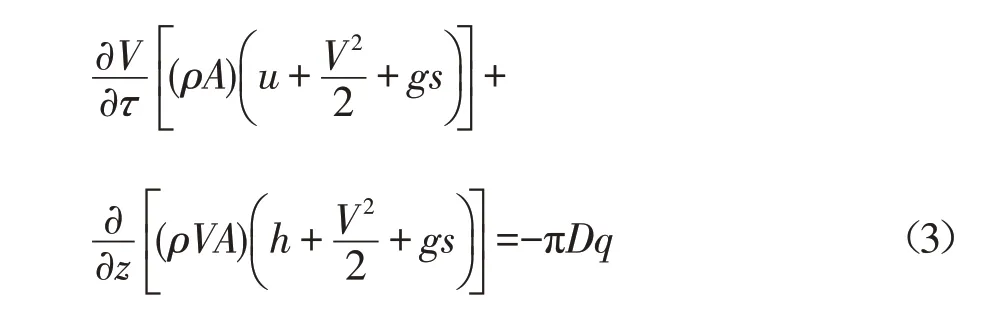
式中：s 为原油比熵，J/（kg·℃）；u 为原油比内能，J/kg；h为原油比焓，J/kg；q为单位时间内原油在单位管壁面积上的散热量，J/（mm2·s）。

由质量守恒方程、动量守恒方程和能量守恒方程得油流的换热方程：

式中：Cp为原油定压比热容，J/（kg·℃）；T 为原油温度，℃。

1.2 结蜡层、管壁和防腐层的传热方程

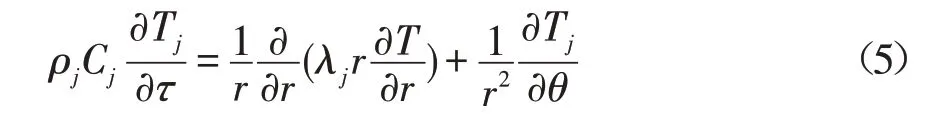
式中：Cj为第j 层（结蜡层、管壁和防腐层）比热容，J/K；λj为第j 层（结蜡层、管壁和防腐层）导热系数，kcal/（m·h·℃），其中，j=1、2、3，分别表示结蜡层、管壁和防腐层，其中1 kcal=4.184 kJ；r 为径向位置，mm；θ为环向弧度，rad。

1.3 土壤导热方程

式中：下标为s 的参数代表土壤的参数；x 为垂直于轴向的水平位置，m；y为深度，m。

1.4 关联方程

管内流体、蜡沉积、管壁、防腐层以及土壤的热交换过程相互关联，满足如下方程：

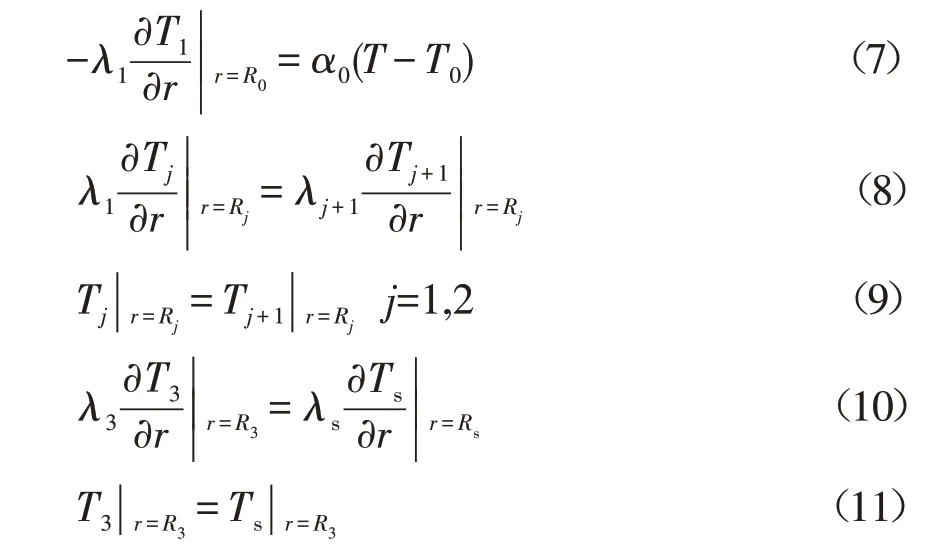
式中：α0为流体对管内壁的放热系数，W/(m2·℃)；T0为管内壁温度，℃；Rj为各层厚度，mm。

1.5 满足的边界条件

埋地管道的界面在物理上是对称的，其计算区域也具有对称性，仅取管道截面右半部分研究，应满足的边界条件如下：

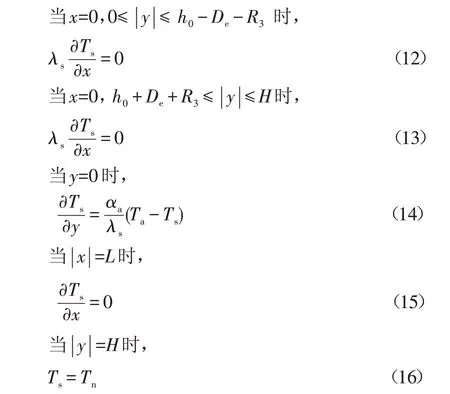
式中：αa为地表向大气的放热系数，W/(m2·℃)；ho为管道埋深，m；H 为纵向热力影响区，m；Ta为大气温度，℃；Tn为恒温层温度，℃；De为管道外径，mm。

2 计算区域离散化及数值计算方法

2.1 计算区域离散化

土壤导热计算区域应为半无限大土壤介质区域。但解析求解需对问题作简化，因而所获得的结果与真实值偏差较大[7]。因此可以通过控制网格划分，获得较高精确度的解。本研究的计算区域限制为原油管道的热力影响区，采用数值计算方法。在数值计算之前要对求解区域离散（网格划分），如图3—图5所示。

图3 土壤区域密集网格划分

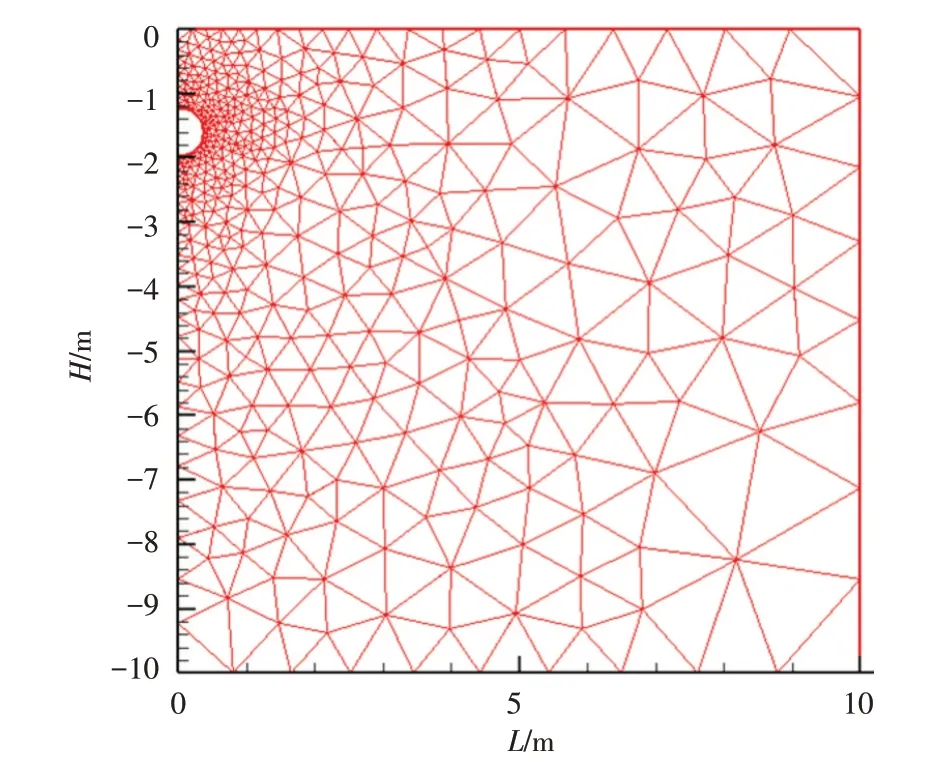
图4 土壤区域稀疏网格划分

图5 结蜡层、管壁和防腐层网格划分及周围的土壤网格

采用有限差分法（FDA）对含蜡原油管道进行离散化，如图6 所示。计算节点从前一个泵站的出口（点1）到后一个泵站的入口（点n）。

图6 管道离散图

2.2 控制方程离散化

对结蜡层、管壁、防腐层及土壤采用控制容积法研究。

2.2.1 油流方程离散

采用有限差分法，对流体非稳态水力-热力耦合方程进行离散求解。如图6所示，沿z方向将管段划分为若干离散的小管段，在ΔZ时间段内，对方程（4）两边进行离散，得到：

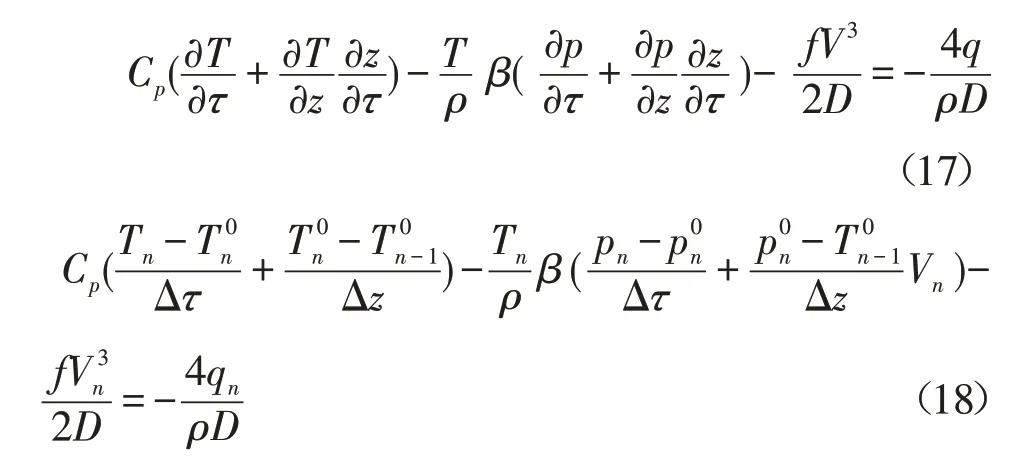
2.2.2 对结蜡层、管壁及防腐层的控制方程离散

结蜡层、管壁、防腐层中的导热方程可以写成如下统一形式：

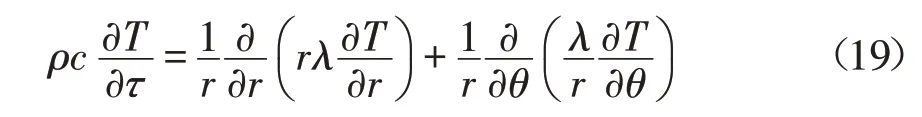
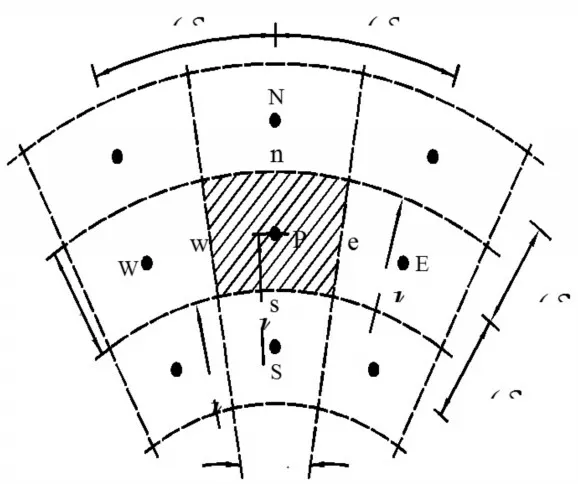
图7 极坐标中的网格系统

结合图7，将式（19）整理成通用的离散化方程形式：

式中：

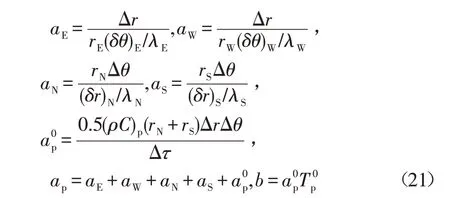
式中：下标E、S、W、N分别代表东、南、西、北4个方位。

2.2.3 土壤控制方程的离散

将计算节点置于三角形的重心，如图7所示，节点P0可视为阴影三角区域的代表，称该三角形为P0的控制容积。离散化导热方程建立起计算节点P0与相邻点P1,、P2、P3的温度的代数关系式。土壤导热方程（6）可以针对任意的控制容积写成如下形式：

3 算例

选取我国东部地区某含蜡原油管道，该管道管体大部分处在冻土区，存在冻胀融沉风险，因此需要了解其温度场变化，从而确定管道安全输量，减小冻胀融沉风险。该管道参数如下：管顶埋深2.2 m；通过对管道运营的土壤进行试验分析得到，土壤分层（0～3 m为含水20%亚砂土，3～10 m为含水25%粉质黏土，10～20 m为基岩），热力影响范围为20 m×15 m；无保温层。冻土导热系数λ1=5.77 kJ/（m·h·℃），融土导热系数λ2=5.77 kJ/（m·h·℃），土壤比热容为C= 1 900 J/( kg·℃) ，土壤表面对大气的放热系数aK= 17. 5 W/ (m2·℃) ，土壤初始温度T0=-12.5 ℃,下边界温度为-5 ℃，地面空气温度TK=-15 ℃。假定冻土厚度6 m，根据管道冬季各站场原油进出站温度（最低2 ℃左右，最高5 ℃左右）分别假定油温为2 ℃和5 ℃，预测油温下土壤温度场及冻融情况。

根据1.1及2.1可得到计算网格划分如图8所示。

图8 网格划分

采用自主开发的网格计算软件，具体参数见2.1，计算结果如图9—图11所示。管道周围绿色线所围为融化区，即不存在冻土，下方接近水平的线是多年冻土下限，同时给出油温5 ℃和2 ℃时，0 ℃等值线，从而确定冻土区域。

图9 2 ℃油温条件下土壤温度场云图和等值线

图10 5 ℃油温条件下土壤温度场云图和等值线

图11 0 ℃等值线

1）油温5 ℃时，管道热力影响较大，不存在冻融情况。

2）油温2 ℃，管道只对周围10 m 内土壤产生热影响，温度场零度线在管道外侧，会造成冻土融化。

本文的土壤参数、地表温度边界、现场冻土情况和油温历史等条件采用了经验数据，在进行数值模拟后得出的结果对管道安全运行具有指导作用。

4 结束语

基于非结构化网格数值计算方法，针对含蜡原油管道外温度场建立了二维非稳态热力计算的数学模型。将该模型应用于某冻土区含蜡原油管道温度数值模拟，通过模拟得到该管道2 ℃及5 ℃油温条件下土壤温度场云图和等值线图，了解管道冻融沉降区域，对于指导管道安全运行和节能降耗具有重要意义。