泥沙突变理论在海底管线冲刷中应用

杨少鹏，拾 兵，杨立鹏

(1. 山东科技大学 海洋科学与工程学院，山东 青岛 266590; 2. 中国海洋大学 工程学院，山东 青岛 266100; 3. 青岛市董家口经济区管委，山东 青岛 266400)

量变和质变是自然界物体变化和发展的普遍规律，而连续性与不连续性变化又是物体变化的两种状态，对于连续变化现象，牛顿的微积分能给出有效的解释；而对于物体的不连续变化状态还没有十分完善的理论。基于此，突变理论才逐渐开始被研究。物体从一种状态形式突然地跳跃到另一种完全不同形式的变化，称为突变。最早的突变理论诞生于文献[1]中，该书用拓扑学、奇点和稳定性的数学理论研究了自然界中的非连续性突变，系统地阐述了突变的理论，为日后突变理论的丰富与发展打下了基础。近年来，随着非线性科学研究地深入，非线性科学被应用到各个领域，并加深了对已有规律认知和了解，同时又获得新的成果。目前，较成熟的初等突变理论主要有7种类型，在各学科中都有涉及[2]。Henley[3]将突变理论应用到地壳断层运动中，提出了一个定性的模型。Potiter-Ferry[4]用突变理论对弹性断裂力学和塑性力学中的失稳现象进行了研究，得出保守系统只有几种失稳的结论。Cubitt和Shaw[5]运用突变理论解释了沉积过程。殷有泉和郑顾团[6]采用尖点突变模型对断层带地震的运动进行了研究。许强和黄润秋[7]采用突变理论对动力分析模型进行了改进，改进后的模型能有效地解释地震作用下土的震动特性。郭火元[8]利用突变理论对大坝的稳定性进行了分析，建立了大坝的稳定态模型。张业民和宋长清[9]运用尖顶突变理论建立了软黏土流动模型。崔鹏和关君蔚[10]将尖点突变模型应用于泥石流的起动研究中，已在泥石流的预防中取得了实效。Graf[11]采用尖点突变模型描述了顺直、弯曲和分汊三种河型相互转化的过程。肖毅等[12]以尖点突变理论为基础提出了定量判定河型稳定性的方法。何文社等[13]根据突变理论，经坐标和拓扑变化，建立了尖点突变模型，得到了泥沙起动的临界条件方程。杨具瑞等[14]利用突变理论得出了非均匀沙起动时的尖点突变模式，并与试验结果进行对比，结果表明尖点突变模式能够反映非均匀沙的起动规律。杨具瑞等[15]在尖点突变理论的基础上采用坐标变换和拓扑变换推导了推移质输沙强度和水流参数的关系式，并用资料进行了对比验证，结果发现在中等强度和高强度输沙时，关系式能较好反应输沙规律，而在低强度输沙时，关系式误差较大，但总体上来说采用尖点突变理论建立的推移质输沙率公式是合理的，基本能反映泥沙的起动和输移规律。王协康等[16]根据泥沙起动的力学规律，导出了泥沙起动条件方程，在此基础上用尖点突变性质对各种泥沙起动现象与机理做了研究。拾兵等[17]利用尖点突变理论建立了波浪作用下泥沙的起动模式，并将计算结果与试验资料对比发现两者基本吻合，说明了该模式可用于波浪作用下泥沙运动的研究。刘勇[18]将突变理论运用到泥沙起动临界条件中去，对波浪作用下的泥沙起动进行了初步探讨。综上可知，尖点突变理论在各领域已取得广泛应用。然而在与泥沙研究关系较密切的海底管线冲刷领域还未见相关的研究报道。通过前人的研究可知道海底管线冲刷涉及管线、海床、水流共同作用，当管线铺设在海床后，引起管线附近流场发生改变，流场的变化反过来会引起泥沙输移的变化(通常是增强)，引起管线局部发生冲刷，最终产生冲刷坑，日积月累造成悬空管线疲劳破坏；而泥沙输移强度增强主要是因为管线铺设于沙床后引起管线前后产生压力差，并且因为管线的阻水作用，使管线附近的水流流速急剧增大，导致泥沙希尔兹数大于泥沙起动的临界希尔兹数，从而引起了泥沙的起动。另外泥沙粒径也是影响泥沙起动与否的一个关键因素，泥沙颗粒越大，泥沙越难起动。上述两者共同作用，最终导致了冲刷坑的产生。因此选取海底管线冲刷达到稳定状态后的冲刷坑深度与管线管径的比值(h=y/D)作为状态变量，希尔兹数(φ)和泥沙粒径的无量纲参数(d*=mdm/d0，d0为泥沙起动粒径，dm为泥沙平均粒径，m为泥沙颗粒之间的密实系数，m=0.75-0.65(2+α)，α=d60/d10为泥沙不均匀程度)作为控制变量，以泥沙突变理论为理论基础，拟探讨海底管线附近泥沙运动的突变关系。

1 海底管线附近泥沙突变模式的建立

根据泥沙突变的非线性理论[19]，泥沙起动的尖点突变模型如图1所示。

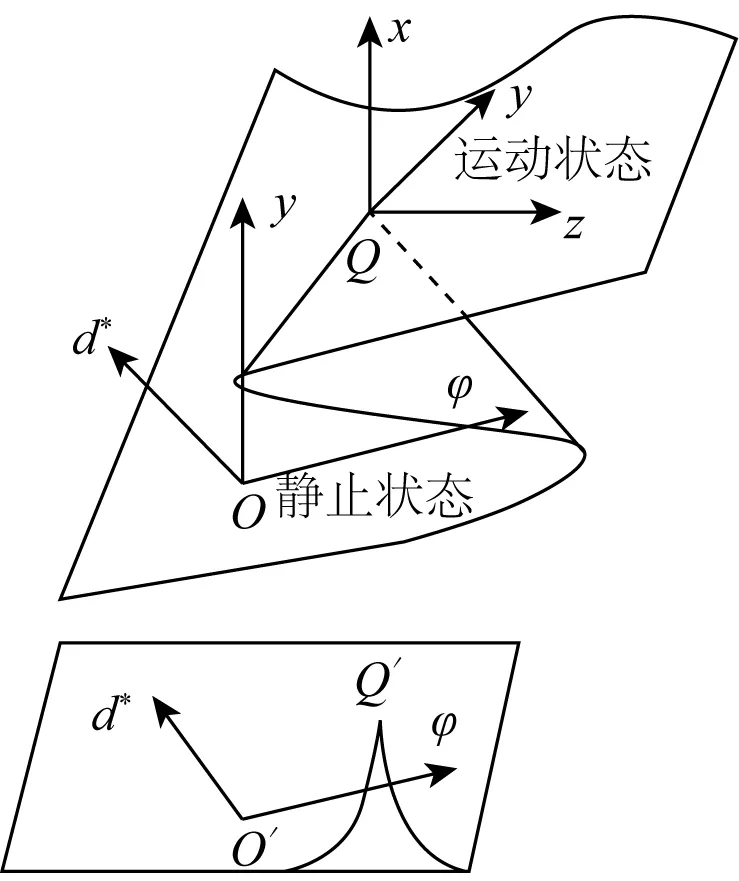
图1 泥沙起动尖点突变模型Fig. 1 The cusp catastrophe model of the sediment incipient motion

图1中突变曲面的标准方程：

x3+xy-z=0

(1)

平面内分支曲线的标准方程：

4y3+27z2=0

(2)

将标准式(1)从坐标系Q(x,y,z)旋转与平移至坐标系O(h,d*,φ)中可得：

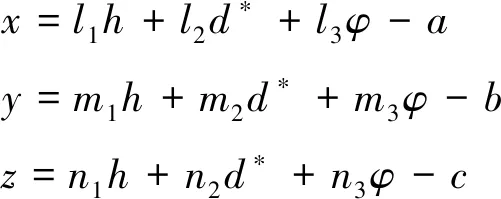
(3)

式中：a,b,c为点Q在O(h,d*,φ)坐标系中的位置坐标值；li,mi,ni(i=1, 2, 3)为原坐标对新坐标的方向余弦。

因图1中h坐标轴与x坐标轴平行，故方向夹角为0，方向余弦：

l1=cos0°=1

(4)

综上可得，曲面在坐标系O(h,d*,φ)内的方程：

f(h,d*,φ)=(h+l2d*+l3φ-a)3+(m1h+m2d*+m3φ-b)(h+l2d*+l3φ-a)-

(n1h+n2d*+n3φ-c)=0

(5)

坐标变换附加条件：

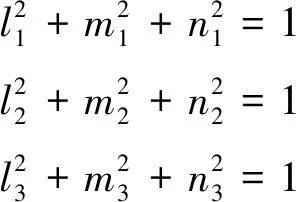
(6)

及

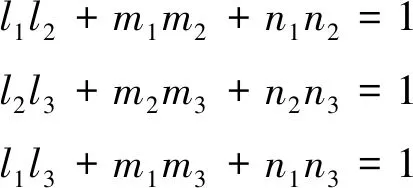
(7)

同为右手坐标系时需满足：

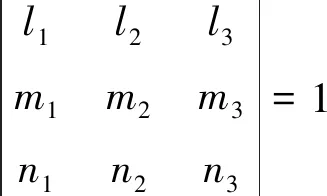
(8)

因曲面经过原点，故

f(0,0,0)=0

(9)

将上述边界条件及坐标变化的附加条件代入式(5)，可得：

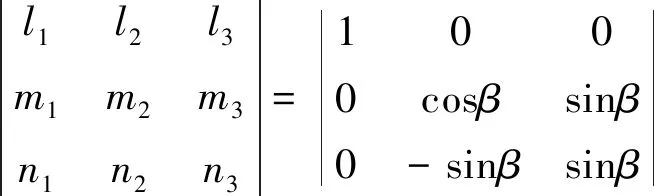
(10)

其中，

β=arctana

(11)

联立式(9)～(11)可得：

a3-a·b-c=0

(12)

将式(10)代入式(5)，可得：

(h-a)3+(cosβ·d*+sinβ·φ-b)(h-a)-(-sinβ·d*+cosβ·φ-c)=0

(13)

将式(11)、(12)代入式(13)，可得：

(h-a)3+a3+h(d*-β′)cosβ-φ(secβ-φ·sinβ)=0

(14)

式中：a为研究区域h的最小值，当泥沙静止时，其起动状态为0，冲刷坑深度为0，故取极限值a=0，β′为泥沙mdm/d0的最小代表值，本文取0.6[20]。将a、β、β′=b/cosβ、β=arctana代入式(14)，可得：

h3+h(d*-0.6)-φ=0

(15)

式(15)即为用尖点突变理论得到的恒定流作用下海底管线冲刷坑深度的预测公式。

当泥沙粒径和水流流速确定时，d*与φ为已知量，式(15)即为一元三次方程。关于其解可根据判别式判断。

令

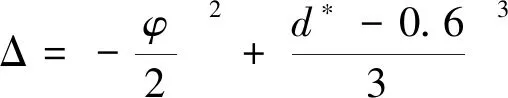
(16)

当Δ>0时，式(15)只有一个实根，且计算结果一般为正值，此实根即为冲刷坑深度值；当Δ=0时，式(15)有三个实根，当d*-0.6=φ=0时，式(15)有一个三零重根，当d*-0.6≠φ时，式(15)至少有两个根相等；当Δ<0时，式(15)有三个不等的实根。当式(15)有两个或三个实根时，需根据实根的正负及实际工况中的条件选择合适的根作为冲刷坑深度值。

2 模型验证

为了检验预测式(15)的准确性，采用Yang等[21]、韩艳[22]、赵恩金[23]、Mao[24]等的试验数据进行了验证。以上四位学者都通过物理试验对单根管线附近的冲刷坑深度进行了研究。其中文献[21-23]都选取了在长25 m，宽5 m，深0.6 m的环形水槽中进行了试验研究，试验选用了中值粒径d50=0.3 mm，孔隙率n=0.4的非黏性沙，沙床高度为0.15 m， 长度为5 m， 试验所用管径为0.1 m左右，管线固定在沙床中央，选取管径前方2 m，高0.5D处的流速作为试验所用的行近流速，水流流速在0.2～0.4 m/s范围内， 水温维持在16°C， 水深为0.4 m。试验过程中每隔一定时间对冲刷坑深度进行监测，待冲刷达到平衡后用精度为0.1 mm的测针对冲刷坑深度进行测量。而Mao[24]的试验参数为：水深H=0.35 m，管径D=0.1 m，泥沙中值粒径d50=0.36 mm，水流流速分别为v=0.3 m/s、0.35 m/s、0.4 m/s。根据以上试验参数，用式(15)进行计算验证。计算过程中，希尔兹数φ可采用Chien等[25]的计算公式：

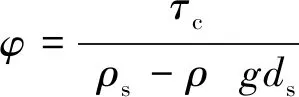
(17)

式中：τc为切应力；ρs，ρ分别为泥沙和水的密度；ds为泥沙平均粒径，可用d50代替。

切应力τc计算公式：

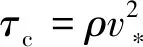
(18)

式中：v*为摩阻流速，可用Einstein[26]对数流速分布公式计算得到：

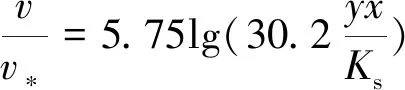
(19)

式中：v为水流流速；Ks为床面粗糙度，对于非均匀沙，Ks常选用一种泥沙粒径d65、d75或d90代替[25]。分别选取d65、d75、d90对计算结果与试验结果进行对比，发现当用d65代替Ks时，结果误差最小，因此选用泥沙粒径d65代替床面粗糙度Ks。x为修正系数，x=f(Ks/δ)，δ为边界层厚度，δ=11.6υ/ν*，υ为流速黏性系数，y为流速测量点的高度，在此可用0.5D代替。

根据上述计算方法，将四位学者测得的冲刷坑深度试验值与相同条件下式(15)的计算值分别列于表1中。对表1中的数据进行对比，可发现试验值与计算值较为接近。

为了更易于直观观察对比结果，将表1中数据全部绘于图2中。图2中y1，y2分别为由式(15)计算得到的冲刷坑深度值和四位学者的试验值。由图2可知，图中各点虽未能与对角线完全重合，但基本分布于对角线附近，这说明理论推导公式式(15)基本能满足于恒定流作用下海底管线局部冲刷坑深度的预测和判断，进而说明将泥沙尖点突变理论应用到海底管线冲刷中是可行的。

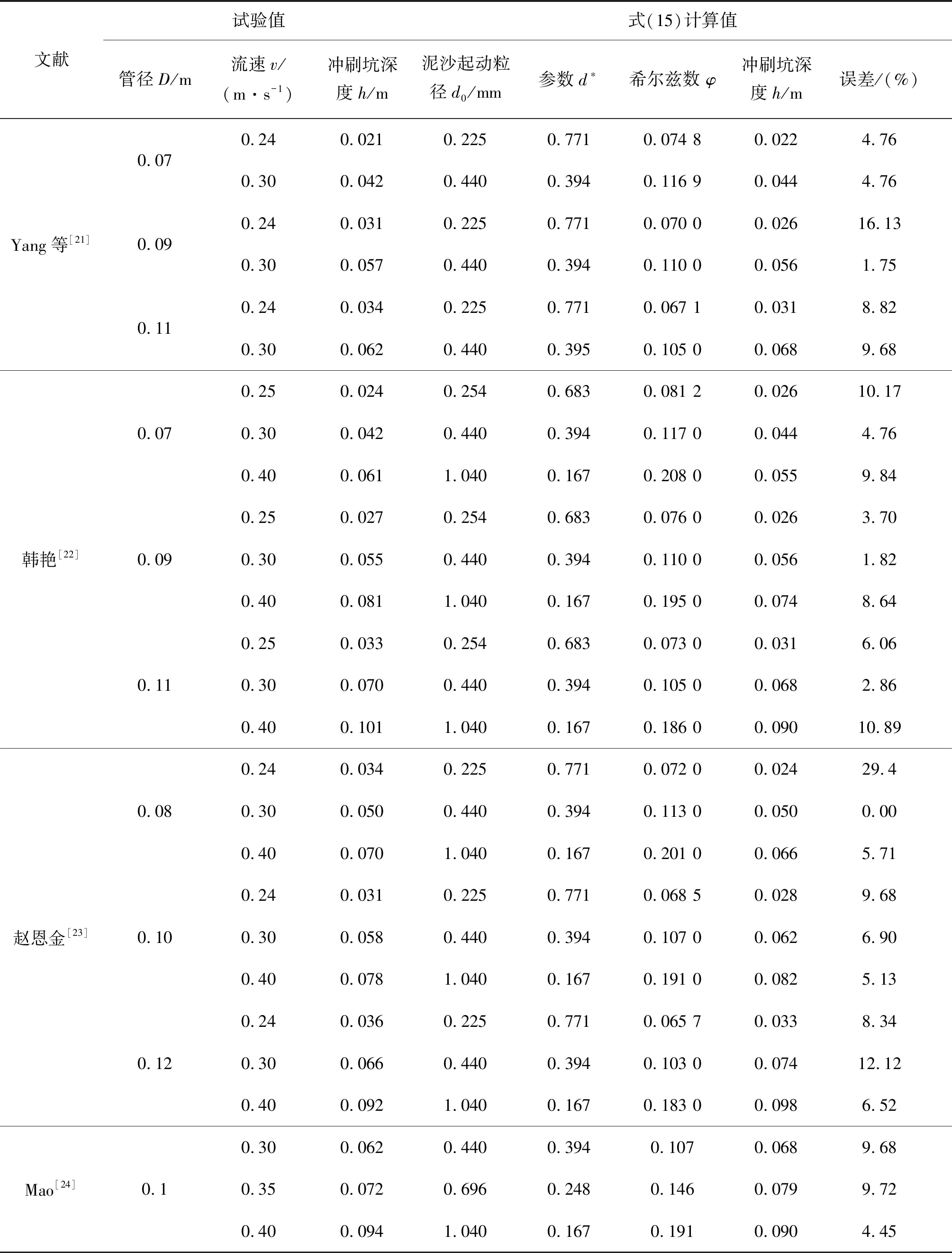
表1 冲刷坑深度试验值与计算值对比Tab. 1 Comparison between the experimental data and the calculated value of scour hole depth

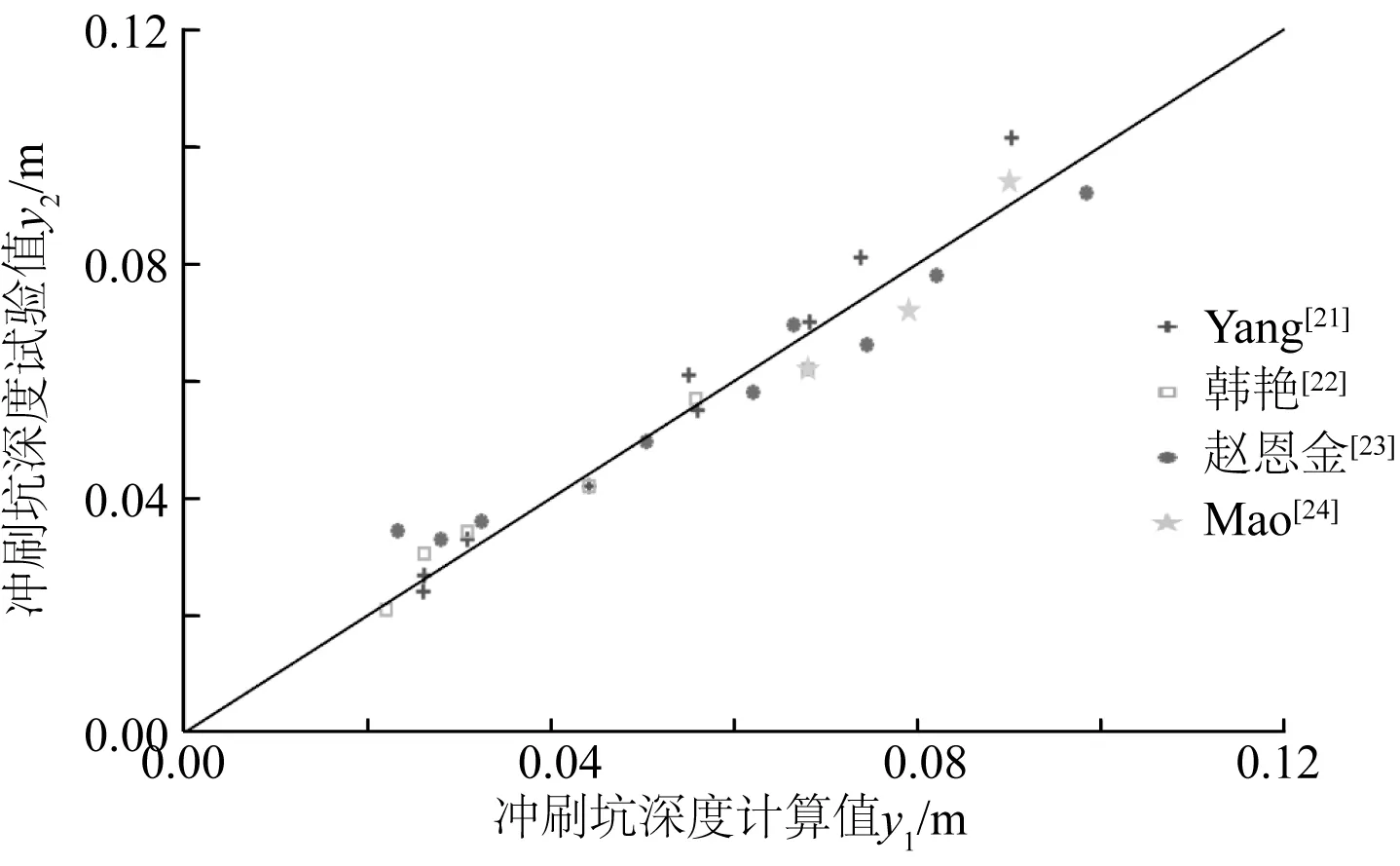
图2 冲刷坑深度计算值与试验值对比图Fig. 2 Comparison between experimental data and calculated value of scour hole depth

3 结 语

通过对尖点突变理论的研究，可将突变理论运用到海底管线局部冲刷坑深度的预测中，经分析得到了恒定流作用下海底管线冲刷坑深度的预测公式。将相同试验条件下用预测公式计算的结果与前人的试验值进行对比可发现，该预测公式基本能满足恒定流作用下海底管线的冲刷坑深度预测与判断，这为管线冲刷坑深度的预测探索了一种新的推算方法。