内置式V型永磁同步电机齿槽转矩优化
2020-04-09邸建忠韩业鹏胡文广谭宝来
邸建忠 韩业鹏 胡文广 谭宝来

摘要:为削弱永磁同步电机的齿槽转矩,通过基于能量法的齿槽转矩解析表达式量化极弧系数对齿槽转矩的影响,将V型永磁同步电机转子结构的复杂几何关系归纳为4个设计变量,使用4个变量的正交表对齿槽转矩进行优化设计,并通过有限元仿真得到使齿槽转矩取最小值的最优设计变量组合。对比优化前、后齿槽转矩峰值可知,所提出的基于田口法的优化设计方案能有效削弱永磁同步电机的齿槽转矩。
关键词:
齿槽转矩; 转子; 能量法; 极弧系数; 田口法; 正交表; 设计变量
中图分类号:TM302; TB115.1
文献标志码:B
Cogging torque optimization of built in V type
permanent magnet synchronous motor
DI Jianzhong, HAN Yepeng, HU Wenguang, TAN Baolai
(INTESIM(Dalian) Co., Ltd., Dalian 116023, Liaoning, China)
Abstract:
To reduce the cogging torque of permanent magnet synchronous motor, the influence of pole arc coefficient on cogging torque is quantitated using analytical expression of cogging torque based on energy method. The complex geometric relationship of rotor structure of V type permanent magnet synchronous motor is divided into four design variables. The cogging torque is optimized using four variables orthogonal table. The optimal combination of design variables to minimize cogging torque is obtained by finite element simulation. The peak value comparison of cogging torque before and after optimization shows that the optimal design based on Taguchi method can effectively reduce cogging torque of permanent magnet synchronous motor.
Key words:
cogging torque; rotor; energy method; pole arc coefficient; Taguchi method; orthogonal table; design variable
0 引 言
隨着磁性材料的不断发展,永磁同步电机越来越广泛地应用于汽车、高精密机床等领域。[1 2]在永磁同步电机绕组不通电时,永磁体与齿槽相互吸引而产生的力矩即为齿槽转矩,因此基本上所有永磁同步电机都存在齿槽转矩。[3 4]齿槽转矩没有增大或减小电机运行时的转矩平均值,但是会使永磁电机在运行过程中产生速度波动、振动和噪声[5],这使得永磁同步电机在高精度、低噪声振动要求场景的应用非常不利。如何减小永磁同步电机的齿槽转矩是永磁同步电机研究的重点之一。
宋洪珠等[6]使用解析法分析永磁电机的齿槽转矩,说明合理的极弧系数和极槽配合能够有效削弱齿槽转矩,但是其只从1个关键因子对齿槽转矩进行优化,未考虑到V型永磁同步电机转子结构的复杂性。夏加宽等[7]使用田口法的正交表对永磁同步电机的槽口宽度、齿靴高度、极弧系数和永磁体厚度等多个设计变量进行优化,最终得到较小齿槽转矩,证明正交表应用于电机优化的合理性,但是其并未深入研究各设计变量对齿槽转矩影响的比重。
本文以能量法齿槽转矩解析式为理论依据,以某额定功率为30 kW的36槽8极永磁同步电机为例,采用田口法正交表与有限元法相结合,对内置式V型永磁电机转子结构的隔磁桥宽度、肋宽、磁钢间角度和永磁体厚度进行优化,并分析其对齿槽转矩的影响比重,最终找到对齿槽转矩影响最大的设计变量,得到使齿槽转矩最小的最优设计变量组合。
1 基于田口法的优化方案
田口法通过正交表选取多个影响因子的试验条件,并对其进行试验[7 8],其基本原理是数学中的排列组合和概率统计。田口法的优势是可以避免因多影响因子而进行大量试验,只通过少量试验即可找到最优组合,因此田口法是工程上广泛应用的优化方法。
内置式V型永磁同步电机齿槽转矩优化设计分为5个步骤:(1)筛选影响V型永磁同步电机齿槽转矩的转子尺寸关键因子;(2)确定每个关键因子的变化范围并各取3~5个值,代表不同取值水平;(3)建立正交表,确定需要计算的因子水平组合;(4)采用有限元法对各个组合进行计算,得到数据结果;(5)分析数据,确定最优组合以及各关键因子对性能指标影响的比重。
2 齿槽转矩的计算
2.1 齿槽转矩解析计算
永磁同步电机的齿槽转矩是电机不通电时永磁体与定子齿槽彼此吸引产生的转矩,齿槽转矩Tcog可表述为不通电时电机的磁场能量W相对于转子位置角α的导数,即
Tcog=W/α(1)
假定铁芯磁导率无限大,永磁材料磁导率与空气一致,则
W≈Wg=12μ0∫B2dV(2)
式中:Wg为气隙磁场能量。对于任意位置角α,
B=Br(q)hm/(hm+g(q,α))(3)
式中:B为气隙磁密沿电枢表面的分布值;q为转子位置角;Br(q)和g(q,α)分别为永磁材料剩磁函数和有效气隙长度函数;
hm为磁钢充磁方向的长度。将式(3)代入式(2)得
Wg=
12m0∫LFe0∫R2R1∫2π0
B2r(q)hmhm+g(q,a)2rdqdrdL
(4)
式中:m0为空气磁导率;LFe为电枢铁芯轴向长度;R1为转子外径;R2为定子内径;r为转子内径;L为铁芯长度。[9 10]
對B2r(q)和hm/(hm+g(q,α))进行傅里叶变换,即
B2r(q)=k2pαpB2s+∞n=12nπk2pB2ssin(nπαp)cos(2npq)(5)
hmhm+g(q,a)2=G0+
∞n=1Gncos(nz(q+α))(6)
式中:kp为每极磁钢总宽度与每极极弧长度的比值;p为极对数;αp为极弧系数;Bs为磁钢剩磁;n为使nz/2p为整数的整数,z为电机定子槽数;
G0和Gn的表达式参见文献[10]。
由式(5)可以看出,B2r(q)对齿槽转矩有较大影响,而极弧系数αp对B2r(q)有很大影响。
2.2 关键因子确定
由齿槽转矩解析计算可知,改变极弧系数αp能够削弱齿槽转矩。内置式V型永磁同步电机极弧系数定义为电机转子永磁体所跨的弧长与极距之比。由于两个弧在同一个圆上,因此弧长之比等同于各自所对应的圆心角之比,见图1。
αploe为电机一极对应的电角度,αpm为永磁体所跨弧长所对应的
电角度,则极弧系数αp=αpm/αploe。
内置式V型永磁电机转子结构见图2。转子结构参数较多且彼此互相影响,不利于使用正交表进行方案优化,需要对其进行筛选和总结。
由图1和2可知,改变肋宽Rib相当于改变极弧系数,因此Rib为关键因子之一。
研究发现,HR与O2是相互影响的,保持其他参数不变,改变O2时会影响HR,因此不能将O2单独作为关键因子。改变HR和O2能够调节磁钢间夹角α,并且保持其他参数不变,因此,将α作为关键因子。同样,永磁体厚度h1和隔磁桥宽度h2也会影响齿槽转矩。因此,选取永磁体厚度h1、隔磁桥宽度h2、肋宽Rib和磁钢间夹角α作为独立关键因子,对内置式V型永磁电机转子结构进行优化。
2.3 正交表法计算齿槽转矩
为研究各参数对内置式V型永磁电机转子齿槽转矩的影响,使用Maxwell对某额定功率30 kW的36槽8极永磁同步电机进行分析,其原始方案主要参数见表1。每个关键因子取4个水平值(见表2),能够包含转子各参数对齿槽转矩的所有影响。
如果采用正常试验的方法对表2各关键因子进行组合,则有44组方案才能找到最优齿槽转矩组合,而采用正交表计算只需要4×4组方案,可大幅减少计算次数,节约计算时间和计算成本,并且可保证计算结果准确。
对于4个关键因子、4个水平的问题,正交表选用L16(44),其中:L为正交表代号;16为正交表的行数,即试验次数;44表示4个水平的4个关键因子。试验方案正交表见表3。
按表3中的16组方案建立模型,采用有限元法计算其齿槽转矩,结果见表4。
2.4 有限元法计算齿槽转矩
16组方案齿槽转矩的平均值为
Tm=16i=1Tcog,i/16=0.725 4 N·m(7)
式中:Tcog,i为表4中第i组方案的齿槽转矩。计算每个关键因子在每一水平下的齿槽转矩平均值,例如
Rib在2水平的平均值计算式为
Tm,Rib,2=(Tcog,2+Tcog,8+Tcog,9+
Tcog,15)/4(8)
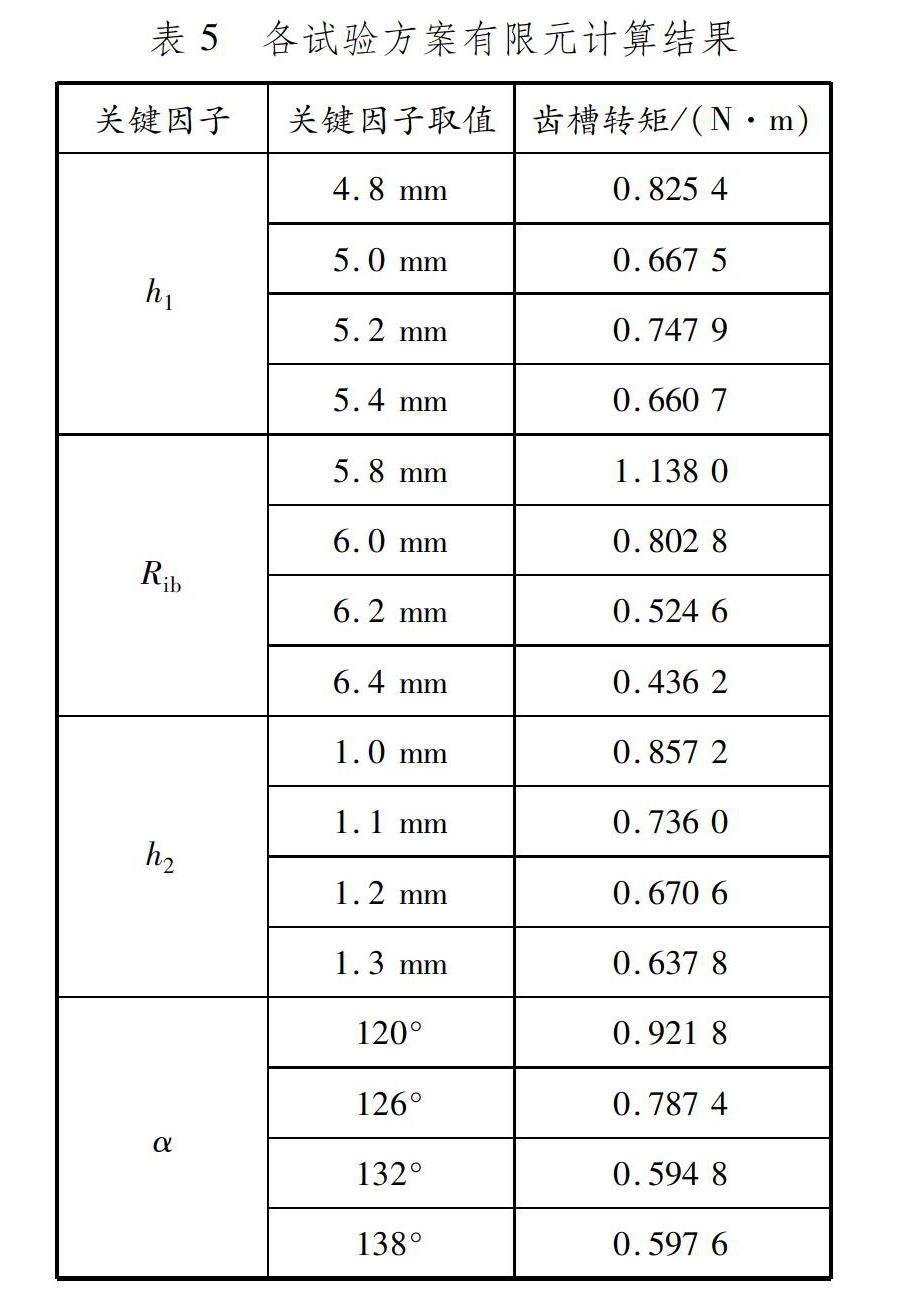
各试验方案有限元计算结果见表5。
根据田口法,若要齿槽转矩最低,则按每个因子各水平下齿槽转矩最小时取值,即h1=5.4 mm、h2=1.3 mm、Rib=6.4 mm、α=132°时为最优组合,此时有限元法计算得到齿槽转矩为0.288 2 N·m,由表1参数计算得到原始方案齿槽转矩为0.981 1 N·m,优化方案齿槽转矩仅为原始方案的29.4%。
2.5 关键因子对齿槽转矩影响所占比重
将式(1)得到的齿槽转矩的总值,与表5中每个关键因子在每一水平下的齿槽转矩平均值对比,可求得每个关键因子对齿槽转矩影响所占的比重[4],即
Px=44j=1(Tm,x,j-Tm)2(9)
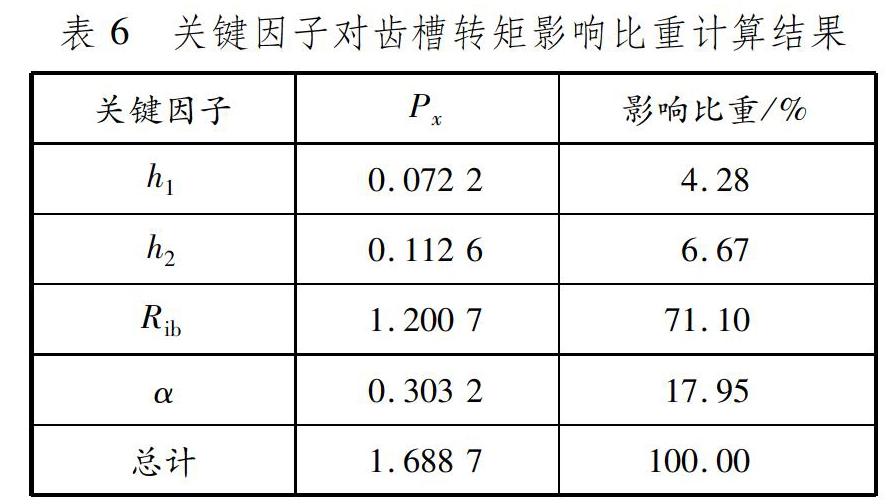
式中:Px为x关键因子的齿槽转矩影响值;下标x代表4个关键因子h1、h2、Rib和α;j为关键因子的4个取值水平;Tm,x,j为表5中x关键因子j水平下齿槽转矩的平均值。根据式(9)计算各关键因子的影响比重,结果见表6。
2.6 结果分析
由表6可知:胁宽Rib对齿槽转矩的影响最大,主要是由于Rib改变极弧系数;磁钢间夹角α也占据相当比重,可知用α代替O2作为关键因子的思路更有效,而且选用α可以使转子各参数之间的复杂关系得以简化。永磁体厚度所占比重只有4.28%,根据设计方案应以节省材料和尽量保持参数与原始方案相接近的原则,此处永磁体厚度仍取5.0 mm。最终优化方案为h1=5.0 mm,h2=1.3 mm,Rib=6.4 mm,α=132°,有限元计算得到此时齿槽转矩为0.320 1 N·m,与由表1参数计算得到的原始方案齿槽转矩0.981 1 N·m相比,优化方案齿槽转矩仅为原始方案的32.6%。优化前、后的齿槽转矩波形对比见图3。
3 结 论
以降低齿槽转矩为目标,以节省永磁体材料和尽量保持性能参数与原始方案相接近为原则,提出一种利用田口法削弱永磁同步电机齿槽转矩的优化方案,通过将复杂转子结构拆解成4个影响齿槽转矩的设计变量,结合有限元仿真分析,快速准确地得到使齿槽转矩最小的最优设计变量组合。分析各设计变量对齿槽转矩影响所占比重,对比优化方案与原方案可知,齿槽转矩被大幅削弱,验证田口法对齿槽转矩优化的简便性和准确性。
参考文献:
[1] 张岳, 曹文平, JOHN M. Design of an interior permanent magnet synchronous motor(PMSM) for EV traction [J]. 电工技术学报, 2015, 30(14): 108 115. DOI: 10.3969/j.issn.1000 6753.2015.14.015.
[2] 樊英, 谭超. 内置式交替极永磁同步电机性能及机理研究[J]. 电工技术学报, 2018, 33(11): 2414 2422. DOI: 10.19595/j.cnki.1000 6753.tces.170506.
[3] 唐任远. 现代永磁电机理论和设计[M]. 北京: 机械工业出版社, 2015.
[4] LU Y P, LI Y. Tooth slot cogging torque and noise analysis of permanent magnet motors[C]// Proceedings of 5th International Conference on Electrical Machines and Systems(ICEMS). Shenyang: IEEE, 2001: 860 862. DOI: 10.1109/ICEMS.2001.971813.
[5] KO H S, KIM K J. Characterization of noise and vibration source in interior permanent magnet brushless DC motors[J]. IEEE Transactions on Magnetics, 2004, 40(6): 3482 3489. DOI: 10.1109/TMAG.2004.832991.
[6] 宋洪珠, 韩力. 极弧系数与极槽配合对直驱永磁同步发电机齿槽转矩的影响[J]. 微电机, 2011, 44(12): 10 13. DOI: 10.3969/j.issn.1001 6848.2011.12.003.
[7] 夏加宽, 于冰, 黄伟. 减小齿槽转矩的永磁电机结构优化设计[J]. 电气技术, 2009(12): 23 25. DOI: 10.3969/j.issn.1673 3800.2009.12.008.
[8] 兰志勇, 杨向宇, 王芳媛, 等. Taguchi方法在内嵌式正弦波永磁同步电机优化设计中的应用[J]. 电工技术学报, 2011, 26(12): 37 42. DOI: 10.19595/j.cnki.1000 6753.tces.2011.12.006.
[9] 王秀和, 楊玉波, 丁婷婷, 等. 基于极弧系数选择的实心转子永磁同步电动机齿槽转矩削弱方法研究[J]. 中国电机工程学报, 2005, 25(15): 146 149. DOI: 10.3321/j.issn:0258 8013.2005.15.027.
[10] 杨玉波, 王秀和, 丁婷婷, 等. 极弧系数组合优化的永磁电机齿槽转矩削弱方法[J]. 中国电机工程学报, 2007, 27(6): 7 11. DOI: 10.3321/j.issn:0258 8013.2007.06.002.
(编辑 武晓英)
