几类含定性因子的复合型混料模型的I-最优设计
2020-04-09叶婉颖朱小渊张崇岐
叶婉颖, 朱小渊, 张崇岐
(广州大学 经济与统计学院,广东 广州 510006)
0 引 言
混料试验设计属于试验设计学科的一个重要分支, 它被广泛地应用在工农业生产和科学研究中[1], 且试验的响应值只取决于混料中各成分的比例[2-3]. Scheffé[4]为这类试验提出了一套规范的理论. 在q分量混料系统中,令xi表示混料中第i个成分的比例. 在混料试验中, 试验域是被限制在q-1维正规单纯形内的.
Sq-1={(x1,x2,…,xq):xi≥0,
(1)
而通过变形得到的一种适用于混料试验的回归模型被称为混料规范多项式模型. 随后, 为了克服单纯形-格子设计试验点数过多以及在预测精度上的不足, Scheffé提出了模型各项更具有对称性的单纯形-中心设计. 该设计将各试验点安排在单纯形整体及所有低维单纯形的中心上, 对应的q分量中心多项式形式为
(2)
其中,βi,βij,…,β12…q分别表示中心多项式(2)中各项的待估参数.
一个试验的结果通常会受到多个不同因子的影响, 这些因子可能是定量的, 也可能是定性的, 各因子之间还可能存在对抗或协同作用[5]. 通常经典的混料试验只讨论定量混料分量, 在实际中, 若混料响应值除受混料分量影响外,还受到如外界温度等定性因子的影响, 则需在经典混料试验模型的基础上将定性因子纳入考虑后,再对该类问题进行拟合[6]. 在试验设计领域中, 含定性因子的已有研究有对混料分量是定性因子情形的讨论[7], 对当因子为定性因子且在试验上有约束的区组设计的讨论[8-10], 关于含定性因子的一般模型和多响应模型的提出及研究[11-12], 以及对含定性因子的混料模型的D-最优和A-最优设计的充要条件和半解析解的研究[5]. 常见的含定性因子混料模型的形式为引入名为“过程变量”的独立变量, 再通过构造考虑所有混料分量和过程变量的混合模型或分离模型, 或是构造一种将混料分量独立变换后的模型来进行之后的数据分析[13]. 另一种模型形式是将在中心组合设计基础上提出的含定性因子模型引入混料试验中[11].
在第j水平上, 将一个包含了q个定量因子和一个水平数为s的定性因子的一般模型表示为
x∈⊆Rq,j= 1,2,…,s
(3)
其中,y(j,xT)是试验点x=(x1,x2,…,xq)T∈对应第j个水平下的响应值.和均为已知的给定函数向量. {βj,j=1,2,…,s}和γ则分别为函数向量的未知参数向量集合和未知参数向量,为定量因子的试验域,Rq表示q维实数域. 在模型(3)中,表示回归函数中定量因子与定性因子之间存在交互效应的部分, 这部分响应函数随着定性因子水平的变化而有所不同; 而则是指定量因子与定性因子之间不存在交互效应的部分, 该部分是总效应中不随定性因子变化而变化的部分, 即在每个定性水平上都保持不变.
近二十年来在混料试验中, 最常被研究的是最优设计[14-18]. 最优设计准则的一个重要理论是等价定理(KWT)[19]. 近年来, 在生成响应曲面设计的标准中, 基于预测的最优准则被广泛应用. 使用预测响应值的方差函数作为设计混料试验起点的说法,在关于混料试验的开创性文章中就已提出[4].I-最优准则是一个常用的基于预测的最优准则, 它是在给定的试验域上寻求使得预测值方差函数的平均值达到最小的设计[20]. 由于良好的预测特性对于优化至关重要, 因此,I-最优准则常被用于优化二阶模型[21]. 利用平均预测方差的定义[22], Lambrakis[23-24]正式定义了两种特殊类型混料设计的I-最优性准则. 关于混料试验设计的两本专著则简要提及了I-最优性准则[16,25]. Lambrakis[24]、Laake[26]、Liu等[27]和Sinha等[18]给出了Scheffé模型的I-最优混料设计结果.关于中心多项式[27-29]、可加混料模型[30]和Becker模型[31]等的I-最优设计也已有了相关研究.
本文的主要工作是研究在含定性因子的情况下混料模型的I-最优设计, 因此,需要给出含定性因子混料模型的矩矩阵的定义, 进一步通过具体模型的近似I-最优配置的引例得到相关定理.
1 准备知识与相关记号
y=βTf(x)+ε
(4)
其中,y表示在点x∈处的响应观测值向量,x=(x1,x2,…,xq)T是试验域中的一点.f(x)=[f1(x),f2(x),…fm(x)]T是关于试验点x的已知函数向量,β是m维未知参数向量. 假定随机误差ε是各分量独立同分布于均值为0、方差为σ2的正态分布的随机向量.
(5)

假设响应值之间互相独立, 且方差不变, 考虑模型的混料应用情形,在第j水平上, 包含了q个定量因子和一个水平数为s的定性因子的复合型混料模型通常有以下形式:
(1)定性因子与定量因子之间存在着线性效应, 协同或对抗效应仅存在于不随定性因子水平不同而变化的部分时:
x∈⊆Sq-1,j=1,2,…,s
(6a)
(2)定性因子与定量因子之间存在着协同或对抗效应, 不随定性因子水平不同而变化的固定部分存在着线性效应时:
x∈⊆Sq-1,j=1,2,…,s
(6b)
(3)所有线性效应、协同或对抗效应都存在于定性因子与定量因子之间时, 在这种情况下的模型与不含定性因子的二阶响应曲面模型并无差异, 仅仅是将一般模型放在定性因子的不同水平上进行了拟合:
x∈⊆Sq-1,j=1,2,…,s
(6c)
x∈⊆Sq-1,j=1,2,…,s
(7)
则在第j水平上, 一个包含了q个定量因子和一个水平数为s的定性因子的广义复合型混料试验模型形式为
γT)T=gT(j,xT)θ,x∈Ω,j= 1,2,…,s
(8)

ξ(j,xT)=ζ(j)×ηj(x)
(9)
其中,ζ(j)及ηj(x)分别是和Sq-1上的边际设计和条件设计.
本文将在以下三种实际中常用的低阶混料模型的基础上, 对它们含定性因子的情况进行研究.
(1)q分量一阶规范多项式模型, 简称{q,1}多项式模型:
(10a)
(2)q分量二阶规范多项式模型, 简称{q,2}多项式模型:
(10b)
(3)q分量中心多项式模型:
(10c)
D-最优准则所选取的设计是使信息矩阵的行列式达到极大值, 从而使得模型未知参数向量β的置信椭球体的体积达到最小的设计, 即使得D-最优准则关于信息矩阵的判定函数ΦD[M(ξ)]满足
(11)
的设计[14,32].
I-最优设计是使得平均预测方差
(12)
引理1[17](I-最优等价定理) 设计ξ*是I-最优设计当且仅当I-准则下的判决函数ΨI(x,ξ*)对任一x∈满足下列不等式:
ΨI(x,ξ*)=fT(x)M-1(ξ*)BM-1(ξ*)f(x)-
tr(M-1(ξ)B)≤0
(13)
其中, 矩矩阵
(14)
2 主要结果
例1 对于三种实际中常用的低阶混料试验模型(10a)~(10c), 考虑定性因子取两个水平(s=2)的情况, 将试验域Ω=Sq-1×上含一个两水平定性因子z的三分量模型具体形式列举如下(其他模型形式类似可得):
(1){3,1}多项式模型
模型(6a)和模型(6c)具体为
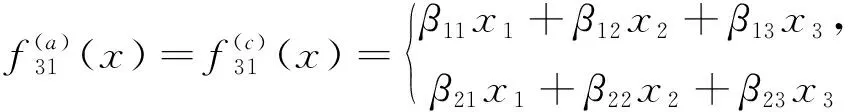
(15a)
模型(6b)具体为
(15b)
(2){3,2}多项式模型(及其转换为含过程变量的模型形式)
模型(6a)具体为
(β1a+β2az)x1+(β1b+β2bz)x2+
肝脏感染中,细菌性肝脓肿是常见且严重的化脓性疾病。随着理论研究及医疗技术的进步,不仅使肝脓肿病死率降至10% 以下,还使其治愈率及诊断率不断提高[2]。对细菌性肝脓肿,目前采用较多的是超声引导下经皮肝穿刺细针抽吸术与经皮肝穿刺置管引流术。一般认为,对于直径≥5cm的脓肿,采用穿刺置管引流术[3]。置管引流术较细针抽吸术明显缩短了患者的痊愈时间。
(β1c+β2cz)x3+γ12x1x2+γ13x1x3+γ23x2x3
(15c)
模型(6b)具体为
γ1x1+γ2x2+γ3x3+(β1ab+β2abz)x1x2+
(β1ac+β2acz)x1x3+(β1bc+β2bcz)x2x3
(15d)
模型(6c)具体为

(β1a+β2az)x1+(β1b+β2bz)x2+
(β1c+β2cz)x3+(β1ab+β2abz)x1x2+
(β1ac+β2acz)x1x3+(β1bc+β2bcz)x2x3
(15e)
在含定性因子的复合型混料模型(8)中, 设计ξ上的信息矩阵为[17]
(16)
其中,
(17)

(18)
当在定性因子的每个水平上考虑相同的条件设计η时, 模型在设计ξ上的信息矩阵可简化为
(19)
而当ζ(j)是上的均匀设计时, 即此时,模型在设计ξ=ζ(j)×ηj上的信息矩阵可进一步简化为
(20)
其中,Is表示s阶单位阵,1s表示元素全为1的s维列向量. 可以看出, 在实际问题中若是有对边际设计ζ(j)取非均匀设计的需求, 则只需添加上不同权重系数ζ(j)即可.
为简化讨论情况, 下文始终仅考虑在定性因子的每个水平上取相等条件设计η的情况.
引理2[6](混料分类模型的D-最优设计) 当ζ(j)是上的均匀设计时, 模型(8)在D-最优准则下的方差函数为
(21)

(22)
其中,p1表示模型中函数向量f1的维数,p2表示模型中函数向量f2的维数. 当且仅当x为柱点时等号成立.
在对模型求I-最优设计的过程中, 可对I-最优准则进行简化. 首先,将试验域上的平均预测方差的积分形式改写为更易于计算的Gamma函数的形式:
(23)
进一步, 假定试验域是q-1维单纯形全域Sq-1时, 试验域上的平均预测值方差可改写为[24,33-34]
APV=Γ(q)·tr[M-1B]=
(24)
可以看出, 为了得到含定性因子的混料模型的I-最优设计, 求解得到模型的矩矩阵B是重要的一环.
定理1 含定性因子的混料模型(8)的矩矩阵B的形式为
(25)

(26)
证明在含定性因子的混料模型中, 矩矩阵B的形式与一般混料模型的矩矩阵稍有不同, 具体为
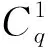
当ζ(j)是上的均匀设计时, 含一个二水平定性因子的{3,2}多项式模型的矩矩阵为模型在设计ξ上的信息矩阵为信息矩阵的逆为其中,从而可得到平均预测方差为
APV=Γ(q)·tr[M-1(ξ)B]=
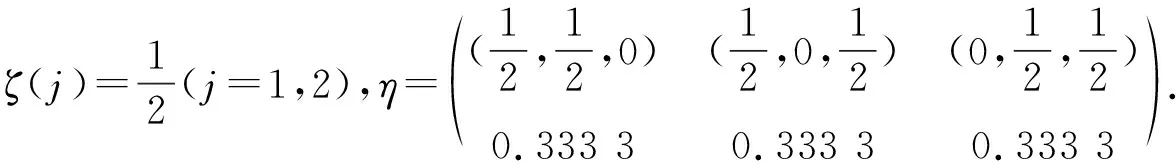
由表1可以看出, 解得的tr[M-1(ξ)B]值的数量级均非常大, 且无论分量数为多少, 最终得到的近似I-最优配置中赋予各顶点处试验点的测度均几乎为0, 即在含两水平定性因子的二阶多项式模型的I-最优设计中, 试验点仅考虑设置于各棱中点处.
图1描述了3≤q≤6时,tr[M-1(ξ)B]的变化情况. 由图1可以看出, 在分量数达到6之前,tr[M-1(ξ)B]的值递减, 到q=5时达到最小. 在实际中为了便于安排试验, 通常考虑的分量数不会太大, 且二阶混料模型最为常用, 故安排分量数为5的试验, 采用含定性因子的{q,2}多项式模型进行拟合即可.

图1 tr[M-1(ξ)B]随q变化图Fig.1 The changes in tr[M-1(ξ)B] with q
定理2 当ζ(j)是上的均匀设计时, 含s水平定性因子的复合型{q,2}多项式模型的近似I-最优设计为ξ(j,xT)=ζ(j)×η(x),其中,表示x的坐标点的循环置换点集,分别表示单纯形的顶点和各条棱中点,ω1、ω2分别表示谱点的配置测度, 且有当定性因子取二水平,q=3,4,5,6时,ω1、ω2的具体数值如表1所示. 表1中的ni(i=1,2)表示的试验点数.

表1 含定性因子的复合型{q,2}多项式模型的近似I-最优设计Table 1 Approximate I-optimal design of compound scheffe′s quadratic model with a qualitative factor
定理3 含s水平定性因子的复合型混料模型(8)中, 设计ξ*为I-最优设计的必要条件是ζ*(j)是上的均匀设计, 即其中,ξ=ζ*(j)×η(x).且当该必要条件成立时有
(27)

(28)
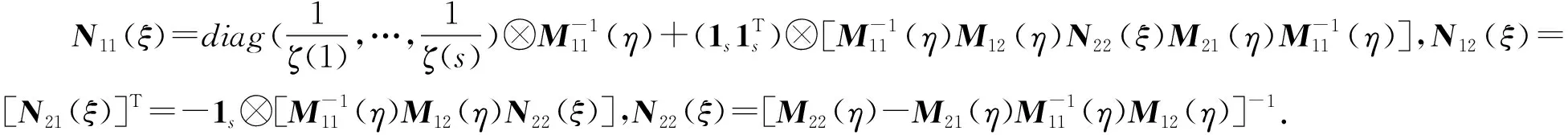
tr[M-1(ξ)B]=tr[N11(ξ)·(Is⊗B11)]+
(1s⊗B12)]+tr[N22(ξ)·B22]=
可进一步将tr[M-1(ξ)B]简写为
s·B21-s·B12+N22·B22].
定理4 当ζ(j)是上的均匀设计时, 模型(8)在I-准则下的方差函数如式(30)所示, 则ξ*是I-最优的充要条件为
dI(j,x;ξ)-tr[M-1(ξ)B]≤0
(29)
其中,tr[M-1(ξ)B]如式(27)所示. 当且仅当x为柱点时, 等号成立.
证明在I-准则下, 方差函数可计算为
dI(j,x;ξ)=
gT(j,xT)M-1(ξ)BM-1(ξ)g(j,xT)=
(30)

由式(13)可知, 设计ξ*是I-最优设计当且仅当I-准则下方差函数dI(j,x;ξ*)对任一x∈Ω满足不等式dI(j,x;ξ*)-tr[M-1(ξ)B]=gT(j,xT)M-1(ξ)BM-1(ξ)g(j,xT)-tr[M-1(ξ)B]≤0,其中, 矩矩阵B由式(25)可得, 且dI(j,x;ξ*)在柱点处的值等于tr[M-1(ξ)B].
推论1 当ζ(j)是上的均匀设计时, 含定性因子的{q,1}多项式模型的近似I-最优设计为ξ(j,xT)=ζ(j)×η(x),其中,表示单纯形的顶点,ω表示谱点的配置测度.当定性因子取二水平, 3≤q≤6时, 具体数值如表2所示. 图2描述了3≤q≤6时,tr[M-1(ξ)B]的变化情况.

表2 含定性因子的复合型{q,3}多项式模型的近似I-最优设计Table 2 Approximate I-optimal design of compound{q,3} polynomial with a qualitative factor

图2 tr[M-1(ξ)B]随q变化图Fig.2 The changes in tr[M-1(ξ)B] with q
推论2 当ζ(j)是上的均匀设计时, 含定性因子的q分量中心多项式模型的近似I-最优设计为ξ(j,xT)=ζ(j)×η(x),其中分别表示单纯形的顶点和各低维单纯形中心点,ω1,ω2,…,ωq分别表示谱点的配置测度. 当定性因子取二水平, 3≤q≤5时, 具体数值如表3所示.

表3 含定性因子的复合型q分量中心多项式模型的近似I-最优设计Table 3 Approximate I-optimal design of compound q centroid polynomial with a qualitative factor
图3描述了3≤q≤5时,tr[M-1(ξ)B]的变化情况.
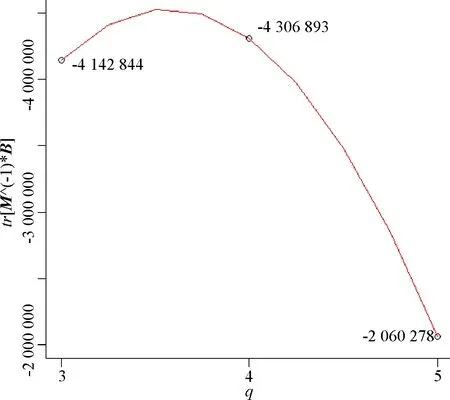
图3 tr[M-1(ξ)B]随q变化图Fig.3 The changes in tr[M-1(ξ)B] with q
由表2和表3可以看出, 在含二水平定性因子的q分量中心多项式模型中解得的tr[M-1(ξ)B]值的数量级仍然非常大, 且赋予各顶点试验点处的测度均几乎为0, 这可能是由于矩阵M-1(ξ)和B的稀疏性. 而图2和图3则描述了q取具体分量值时tr[M-1(ξ)B]的变化情况, 可以看出, 在含二水平定性因子的{q,1}多项式模型和q分量中心多项式模型中,q=5时的近似I-最优设计结果均十分优良. 结合前述可以得出如下结论: 在实际生产生活中, 若对含定性因子情况下的混料试验有预测的需求, 则安排分量数为5的试验时往往能得到较为满意的设计结果.
3 总 结
本文研究了q分量一阶、二阶规范多项式模型和中心多项式模型这三种实际中常用的低阶混料模型含定性因子情况下的I-最优设计问题, 并给出当定性因子为二水平情况下时模型的近似I-最优配置. 得出如下结论: 在混料模型含定性因子时, 除了一阶情形外, 近似I-最优配置中赋予各顶点试验点处的测度均几乎为0, 且解得的tr[M-1(ξ)B]值的数量级均非常大. 当q=5时, 在三种模型中的近似I-最优设计结果均十分优良. 另外, 当分量数超过5时, 易产生维数灾难问题, 使得近似I-最优配置的求解困难呈幂级数增长, 因此,在q≥6的高维情况下可以考虑降维兼引入算法的方法,搜索得到近似最优设计.
