基于递推最小二乘算法的光纤振动定位系统
2020-04-09罗义军
罗义军,尹 棋,李 劲
(1.武汉大学 电子信息学院,武汉 430072; 2.武汉纺织大学 电子与电气工程学院,武汉 430200)
引 言
基于双马赫-曾德尔的分布式光纤振动定位系统对振动感知和应变十分敏感,具有功率损耗小、不受电磁干扰、造价低等优点,在油气管道检测报警以及周界安防中大量应用[1-4],其中扰动定位算法以开环互相关算法和闭环最小均方(least-mean square,LMS)算法为主[5-9]。互相关以其开环结构对信号毛刺,电路噪声敏感,扰动定位稳定性不足[5-10]。LMS的最优准则是使滤波器输出与期望信号误差平方的数学期望最小,根据输入数据的长期统计特性得到的对一类数据的最佳滤波系数[11]。然而在判断一次定位时,已知的仅是采集的一组振动数据,并且对于LMS,滤波器阶数愈高,步长因子和输入信号功率愈大,其失调系数也愈大[11],会直接影响定位结果。
采用闭环递推最小二乘(recursive least-squares,RLS)是对每一组已知数据寻求精确的最佳滤波器系数。因为RLS的最优准则是使滤波器输出与期望信号误差平方累计和最小,RLS收敛速度快于LMS[12-13],避免了固定步长LMS收敛速度和稳态均方误差相互制约的矛盾以及变步长的LMS待调参量多且调节困难的问题。由于滤波器收敛后,滤波器系数波形将近似于sinc函数,且两路信号延迟点数在峰值位置获得[7]。借鉴早迟门同步判决最佳采样位置的原理,以鉴相曲线的近零点值位置作为定位的结果。现场可编程门阵列(field-programmable gate array,FPGA)可以支持高速多路并行运算,非常适合处理数据流,因此系统中定位算法由FPGA实现。
1 光纤定位系统原理阐述
1.1 双马赫-曾德尔定位原理
图1中右侧包含连续激光源;O1,O2,O3为3dB光耦合器;3根分别长为L1,L2,L3的铠装单模光纤;光电探测器D1,D2;环形器C1,C2。左侧是对光电探测器接收信号的处理流程。在没有振动时,经O1耦合的两路相干光同时到达D1,D2。而在长为L2的振动臂上某一点有入侵行为,将存在时间差Δt,且入侵位置P可表示为[4-9]:

(1)

Fig.1 Optical path model and signal processing flow
设采样率为f, 单个采样点表示的定位距离精度r由相邻两个采样点之间的时长决定,r可以通过下式求得[8,10]:

(2)
式中,c为光速,n0为光纤折射率,约为1.46。
1.2 RLS算法及横式滤波器估计时延原理
RLS自适应滤波器是指能够根据环境的改变,采用累计误差平方和为代价函数的准则,自适应反馈调节滤波器系数使得代价函数最小[11]。图2所示为M阶RLS横式滤波器结构。给定一个输入采样序列x(n),x(n-1)…x(n-M+1),并用其冲激响应w0,w1,…,wM-1来表征该滤波器。在某一离散时刻n,滤波器的输出为y(n),先验估计误差eerr用期望响应d(n)与y(n)之差表示,通过迭代反馈使得下一刻的输出值y(n+1)不断地逼近期望信号d(n+1),误差将迫近为0。图中,Z-1表示信号延迟1拍。

Fig.2 Structure of RLS adaptive filters
假定n时刻输入M×1维矢量X(n)=[x(n),x(n-1),…,x(n-M+1)]T,滤波器系数M×1维矢量W(n)=[w0,w1,…,wM-1]T,T表示矢量转置;M×M维迭代矩阵C(n)。振动信号为平稳信号,取遗忘因子λ=1;正则化参量δ为小正实数,与输入信号x(n)的信噪比有关[12-13]。对RLS采用前加窗法,算法流程见下[11-13]。
(1)初始n=0时刻值:

(3)
式中,I是M×M维单位矩阵;迭代过程对n=1,2…,更新增益矢量g(n):
(4)
(2)更新滤波器系数矢量W(n):
W(n)=W(n-1)+
g(n)[d(n)-[X(n)]TW(n-1)]
(5)
(3)更新迭代矩阵C(n):
C(n)=λ-1[C(n-1)-
g(n)[X(n)]TC(n-1)]
(6)
由于滤波器的输入信号x(n)会遍历滤波器的0~M-1级延迟位置。由叠加定理知,相对于x(n)的延迟信号x(n-τ)可由滤波器各级冲激响应w0,w1,…,wM-1,表示为:
x(n-τ)=w0x(n)+…+
wM-1x(n-M+1)
(7)
式中,τ为延迟点数。又根据卷积定理:
x(n-τ)=x(n)*δ(n-τ)
(8)
式中,δ(n)为采样冲激响应函数。取:

(9)
式中,0≤i (10) 即有限长横向滤波器的系数wi与采样函数sinc(i-τ)重合时,滤波器输出近似为延迟信号x(n-τ),且系数最大值wτ的位置为延迟点数τ。 寻找系数峰值的位置i=τ直接判别在噪声存在的情况下易产生偏差[16]。假定不在峰值点对信号采样,在i=τ-φ位置早采样,在i=τ+φ位置迟采样,早、迟采样的绝对值都比峰值采样值的绝对值小,φ表示偏离系数峰值位置的点数。再以迟采样时刻值减去早采样时刻值,得到鉴相曲线。由于收敛的系数相对于最佳采样时刻i=τ是偶函数(sinc(i-τ)),早、迟采样值的绝对值应该相等。因此,采样峰值的位置就是在鉴相曲线为零的位置。 基于图1左侧电信号处理流程,搭建了图3所示的硬件平台。D1,D2是PIN激光管,将光信号转换为电小信号,以高精度低噪声的双运放OPA2227放大5倍。经过截止频率为100kHz的有源低通滤波器UAF42滤出有用振动信号。全差分运算放大ADA4930将单端信号转换为差分信号,进一步地抑制噪声影响,并放大2倍驱动后级高速模-数转换器(analog-to-digital converter, ADC)。ADC选取ADI公司推出的低功率、16bit、双通道、最大采样率为125MHz的ADC9268,采样时钟定为10MHz。FPGA选取Altera公司的Cyclone Ⅳ系列高性价比低功耗、逻辑资源丰富的EP4CE115F23I7实现振动信号识别及定位算法。 Fig.3 Circuit block diagram of signal processing 图4为处理ADC采集的D1,D2两路信号FPGA程序框图。两路信号经过64阶低通滤波后以两路信号的方差判别振动起点,将RLS每次迭代获取的滤波器系数经过滑动平均过程,降低噪声对于后级早迟门判决最大系数位置的影响,最后将估计的延迟点数转换为实际扰动位置。 Fig.4 FPGA block diagram 2.2.1 振动起点识别 光纤在静止状态下发生振动时会导致ADC采集的数据离散度迅速增大,可以取一滑动窗内的定点数据量的方差来判断振动起点。方差获取的simulink框图(见图5),任意一路信号方差值连续多次超过阈值,则识别为振动的起点。之后所采集的数据均为振动数据,用于RLS定位算法。图6为Quartus Ⅱ中计算方差的Verilog顶层例化模块框图。 Fig.5 Simulation block diagram of calculating the variance Fig.6 FPGA block diagram of calculating the variance 2.2.2 RLS算法FPGA实现 在一段160m光路上进行定位测试,以10MHz(r=±10m精度)采样后两路信号最大延迟点数为16,取RLS横向滤波器为M=20阶实现定位。对于长距离的定位,可以相应地增加滤波器的阶数,而这会影响算法收敛速度,也会成倍增加FPGA硬件资源消耗。可先对采集的数据进行下抽,降低定位精度,获取扰动的大致距离区间。在此基础上,以原来的采样率进一步的细定位[17]。算法迭代流程中计算滤波器输出y(n),M×1维增益矢量g(n),M×1维系数矢量W(n)及M×M维矩阵C(n)均是行矢量乘以列矢量的乘、加基本结构,因此FPGA中基本计算单元设计为1×M维行矢量乘以M×1维列矢量[18-19]。图7为Quartus Ⅱ中基本计算单元的Verilog例化顶层模块框图。 Fig.7 FPGA block diagram of RLS basic computational unit 此外,迭代更新系数矢量W(n+1)及矩阵C(n+1)则是上一拍的旧值与校正值的迭代累加结构,其基本单元simulink结构见图8。 Fig.8 Simulation block diagram of basic iterating unit 分析迭代流程可知,RLS的运算量主要集中于(4)式和(6)式中状态量的计算和迭代更新[12]。RLS算法每次迭代需要3M2+3M次乘法,1次除法和2M2+2M次加减法,递推的运算次数在O(M2)[12]。算法复杂度结构框图如图9所示。 Fig.9 Analysis of computational complexity for RLS algorithm 2.2.3 滑动平均处理及早迟门 RLS滤波器收敛后,其抽头系数波形将近似于sinc函数主瓣峰,每次迭代更新后获取的系数值也在滤波器理论最佳系数附近,波形不会发生本质性的变化。由于系数迭代从初始值开始至全部振动数据结束,每迭代一次便可以获得一组滤波器系数。可以充分利用每次迭代获取的系数值,让其经过一滑动平均过程,在统计平均的意义上不改变波形本质且能抑制某一次迭代过程因为噪声的随机性而使系数波形随机起伏[20]。图10为滑动平均和早迟门的simulink结构图。 Fig.10 Simulation block diagram of moving-average and early-late door 滑动平均后的系数取φ=1的早迟门相减得到鉴相曲线。图11鉴相曲线计算零值位置的Verilog顶层例化模块框图。 Fig.11 FPGA block diagram of getting position by phase curve 一次振动的时长在500ms以上,其中幅度较强的信号大约集中在最初200ms以内。当ADC采样率为10MHz时,一次振动可以获取幅度较强的信号点数约2×106个数据。RLS具有很快的收敛速率,约迭代1×105次(10ms采样点数)后就可以得到良好的定位结果。因此FPGA设计时,将最初振动幅度较强的信号分为18段分别进行定位计算,记录每一段的定位结果。而后剔除其中定位的最大值和最小值,剩余16段计算结果取平均,作为最终的定位结果。这样,在不增加滤波器阶数和ADC采样率的情况下,提高定位精度同时也抑制噪声而减少误判概率。 基于图1中双马赫-曾德尔光路框图和图3中的光纤振动硬件平台,设计了一套光纤振动定位系统。在一段160m的光路上进行重复敲击实验,选用波长为1550nm,功率可调的稳定化台式激光源,功率输出范围0.1mW~40mW。光路铺设部分选用8芯单模铠装光纤(GYXTW-8B),并将光纤蛇形盘绕在小区围栏上。 在simulink中对开环互相关,闭环最小均方LMS以及递推最小二乘RLS进行定位对比仿真。选择在90m附近敲击光纤,上位机通过千兆网口接收ADC9268采集的振动数据作为仿真源。采样率为10MHz(r=±10m精度)时,simulink中3种定位算法以50×104个采样点计算振动位置。从图12中的仿真结果可以看出,LMS收敛速度明显慢于RLS;而互相关虽也得到振动位置,但随着互相关累加点数增加,相关峰位置改变,稳定性差。比较之下,RLS在10×104个采样点以内已经快速收敛出振动位置(9×10=90m),且定位收敛稳定。纵坐标为D1,D2两路相关信号相差的延迟点数。 Fig.12 Results of positioning simulation 算法收敛后,RLS滤波器系数收敛波形及鉴相曲线如图13所示,纵坐标分别为RLS滤波器系数的值和鉴相曲线的值。 Fig.13 Filter coefficient value and phase curve 实验中选择在60m附近,以手握光纤、攀爬护栏、轻敲、重敲等模拟不同的实际扰动环境。图14为某一次60m处攀爬护栏,用SignalTapⅡ抓取各模块关键信号及ADC采集的振动波形。 在60m附近重复敲击30次,记录每一次上位机接收的定位结果,在MATLAB中绘制出图15。从图中可以大致看出,实际定位误差在±6m。 Fig.14 Vibration wave in SignalTap II Fig.15 Multiple tap positioning results near 60m 运用RLS、滑动平均和早迟门设计出一套光纤振动定位系统,并在FPGA硬件平台上实现快速定位。对比于开环的互相关以及闭环LMS,RLS可以根据环境变换自适应快速的调整参量,针对每一组ADC采集数据得到不同的滤波器系数。并且RLS随着迭代次数增加,单次定位结果稳定不会发生波动,定位收敛速度也是LMS的3倍左右,解决了开环互相关稳定性不足,避免了LMS收敛速度和稳态误差相互制约的矛盾。由于RLS具有快速的收敛性,对振动数据分段定位处理,定位平均值作为最终定位结果,保证定位的稳定可靠,且系统精度保持在±6m。在实际应用中,包括刮风、下雨等大量非人为扰动因素存在的复杂环境,后续工作着重在于对不同振动信号的识别。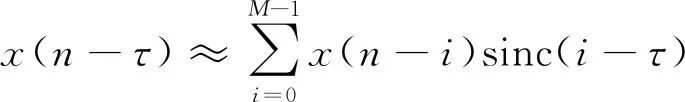
1.3 早迟门原理
2 系统硬件平台及定位算法实现
2.1 光纤定位系统硬件平台

2.2 实现定位的FPGA结构








2.3 定位结果处理
3 实验结果
3.1 simulink中定位算法对比仿真
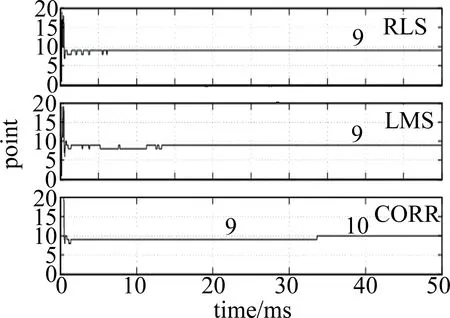

3.2 FPGA定位结果
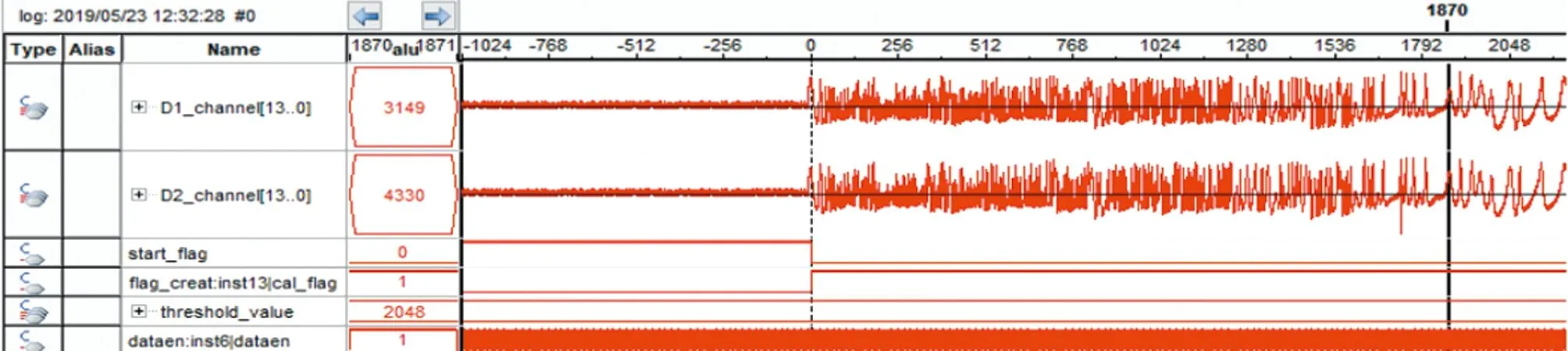

4 结 论
