致密气藏水平井多段体积压裂复杂裂缝网络试井解释新模型
2020-04-09欧阳伟平孙贺东韩红旭
欧阳伟平 孙贺东 韩红旭
1. 中国石油川庆钻探工程公司长庆井下技术作业公司 2. 中国石油勘探开发研究院 3. 中国石油长庆油田公司工程监督处
0 引言
水平井多段体积压裂已成为致密气藏开发的主要技术手段。对于天然裂缝发育及脆性较好的致密砂岩储层,大规模体积压裂后井筒周围会形成形态各异的复杂裂缝网络。目前,改造区体积及压裂缝网形态主要通过微地震监测来获取,但微地震监测不能准确获取储层有效改造体积(SRV)及缝网导流能力的大小,而试井解释则有望成为获取SRV及缝网导流能力的有效手段。关于压裂水平井试井解释模型,早在20世纪90年代就有相关研究[1-5],然而,无论是针对常规油气藏[6-10]、非常规油气藏[11-15]还是裂缝性油气藏[16-17],大部分适用于压裂水平井的试井模型仅假定压裂缝为单一主裂缝,使得试井解释结果与实际情况之间存在着较大的误差,以致于无法准确获取改造区的缝网特征参数。目前,考虑复杂缝网的渗流模型可以分为双重孔隙介质复合模型[18-19]和离散裂缝模型[20-21],其中复合模型将地层划分为主裂缝区、压裂改造区和未改造区,并假定压裂改造区为双重孔隙介质。由于体积压裂产生的裂缝在长度、开度以及间距等方面存在着差异,尤其是在裂缝间距差异较大的情况下,假设压裂改造区为双重孔隙介质将与实际情况存在着较大的偏差。而离散裂缝模型则通过对裂缝进行显式处理来准确描述任意裂缝的形态、方位及导流能力,因此该模型在处理体积压裂复杂裂缝网络上具有明显的优势。根据网格划分及求解方式的不同,离散裂缝模型又分为嵌入式和非结构化离散裂缝模型[22];前者对基质进行结构化网格划分,再将裂缝嵌入基质网格系统中,并根据裂缝与基质的相交情况形成裂缝网格,大大降低了网格数量,提高了计算速度,但较难满足试井动态模拟的早期高精度要求[23-24];而后者采用非结构化网格来划分储层,并使其与裂缝网络相匹配,然后对裂缝进行降维处理,在保证裂缝描述精度及计算速度的同时,可以满足试井动态模拟的早期精度要求[25-26]。但是,目前考虑复杂裂缝网络的非结构化离散裂缝试井模型还鲜有报道。
为此,笔者基于非结构化离散裂缝模型,建立了一种考虑复杂裂缝网络的致密气藏压裂水平井试井模型,然后利用三角单元和线单元混合的有限元方法对模型进行求解,进而获得了不同缝网形态(矩形、椭圆形及双曲形)下的水平井试井理论曲线;在此基础上,分析试井曲线特征及其影响因素,并与常规单一裂缝模型的试井曲线进行了对比;最后应用新模型对鄂尔多斯盆地庆阳气田二叠系山西组山1段致密气藏一口多段体积压裂水平井进行了试井解释,以验证新模型的可靠性及实用性。
1 复杂裂缝网络描述
体积压裂形成的复杂裂缝网络形态各异,根据微地震监测结果,可大致分为等宽、中间宽两端窄及中间窄两端宽3种形态。为此,分别采用矩形、椭圆形及双曲形3种类型缝网来描述改造区,并假定改造区形成的裂缝正交,如图1所示。将改造区的裂缝分为主裂缝、次裂缝及支裂缝3个级别,其中主裂缝和次裂缝与水平井段所在的方向垂直,支裂缝与水平井段所在的方向平行。

图1 复杂裂缝网络形态示意图
常规单一裂缝模型只采用裂缝长度及导流能力来描述裂缝,而缝网模型采用改造区长度、宽长比、横向缝网密度、纵向缝网密度以及3种类型裂缝的导流能力共7个参数来描述缝网。
2 试井数学模型及求解
2.1 物理模型及假设条件
考虑致密气藏储层中有一口水平井,该井经过多段体积压裂后形成复杂缝网(包含主、次及支裂缝),裂缝均正交。流体在裂缝中的流动为一维流动,在储层中的流动为二维流动。主裂缝中的流体直接进入井筒,次裂缝与支裂缝中的流体必须通过主裂缝才能进入井筒。模型假设条件为:①原始储层均质、有界且渗透率各向同性,考虑储层的应力敏感效应,忽略裂缝的应力敏感效应;②忽略气体滑脱效应[27],考虑气体流动为单相渗流,且满足达西定律;③水平井筒具有无限大导流能力,裂缝均为有限导流裂缝,且导流能力各不相同;④气体压缩系数、黏度、偏差因子等高压物性参数随压力变化而变化,考虑井筒储存效应和表皮效应。
2.2 数学模型
流体在储层中的渗流控制方程为:

流体在主、次、支裂缝中的渗流控制方程依次为:

初始条件为:

内边界条件为:

外边界条件为:

考虑储层应力敏感对渗透率影响的方程为:

拟压力计算式为:
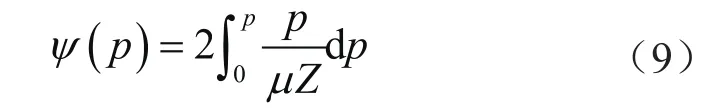
式中x、y表示储层中坐标位置,m;Kr表示储层中气相渗透率,mD;p表示储层压力,MPa;ψ表示拟压力,MPa2(/mPa·s);φ表示有效孔隙度 ;Ct表示综合压缩系数,MPa-1;μ表示气体黏度,mPa·s;t表示生产时间,h;Kf1、Kf2、Kf3表示主、次、支裂缝的渗透率,mD;l表示裂缝中某位置,m;Γin表示内边界;qsc表示标准状态下的产气量,m3/d;T表示储层温度,K;wf1表示主裂缝宽度,m;h表示储层有效厚度,m;C表示井筒储存系数,m3/MPa;N表示沿边界外法线方向向量,无因次;Γout表示外边界;σ表示上覆岩石压力,MPa;Sp表示渗透率应力敏感系数,无因次;Z表示气体偏差因子,无因次;下标w表示井底;下标i表示初始状态。
2.3 模型求解
首先利用非结构化网格离散技术对包含复杂裂缝网络的计算区域进行Delaunay三角网格剖分,剖分后的网格与裂缝网络完全匹配,以椭圆形缝网为例,剖分后的网格离散效果如图2所示。由于对裂缝中流体流动进行了降维处理,使裂缝成为一维线单元,储层为二维三角单元。基于混合单元有限元方法对模型进行求解,如式(10)所示,将整个计算区域划分为流体发生二维流动的储层区域及流体发生一维流动的主、次、支裂缝区域4个部分。在求解数学模型时,利用Galerkin加权余量法推导出储层和3级裂缝单元的有限元计算格式,如式(11)~(14),根据有限元计算格式建立求解矩阵,具体求解方法见本文参考文献[25]。

图2 与裂缝网络相匹配的非结构化网格划分图

储层区域流体二维流动有限元方程为:


主裂缝区域流体一维流动有限元方程为:
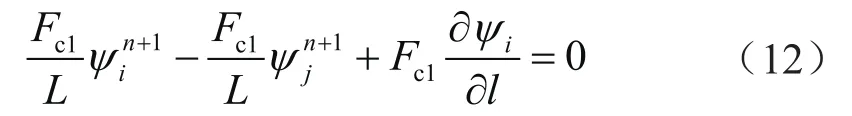
次裂缝区域流体一维流动有限元方程为:
支裂缝区域流体一维流动有限元方程为:

式中Ω表示整个流动区域;Ωm表示储层流动区域;Ωf1、Ωf2、Ωf3分别表示主、次、支裂缝流动区域;Feq代表流体流动方程;wf2、wf3分别表示次、支裂缝宽度,m;A表示三角形网格面积,m2;b、c分别表示有限元单元系数;Δt表示时间步长,h;L表示裂缝一维网格长度,m;Fcl、Fc2、Fc3分别表示主、次、支裂缝的导流能力,mD·m;下标i、j、k分别表示三角形网格结点序号;下标j(k)表示j或者k;上标n表示时间步。
3 计算结果及分析
3.1 结果验证
为了验证本文所建立的模型与求解方法的正确性,假定次、支裂缝的渗透率与储层渗透率一致,则复杂缝网退化为单一裂缝。假设储层初始压力为30 MPa,温度为100 ℃,渗透率为0.1 mD,有效厚度为10 m,孔隙度为10%,水平井筒长度为1 000 m,井筒储存系数为0.5 m3/MPa,压裂段数为4段,裂缝导流能力为500 mD·m,裂缝半长为100 m。将本文模型计算结果与试井商业软件Saphir计算结果进行对比,如图3所示,对于单一裂缝,本文模型与常规经典模型的试井曲线一致,验证了本文模型及求解方法的正确性。
3.2 复杂缝网试井曲线特征
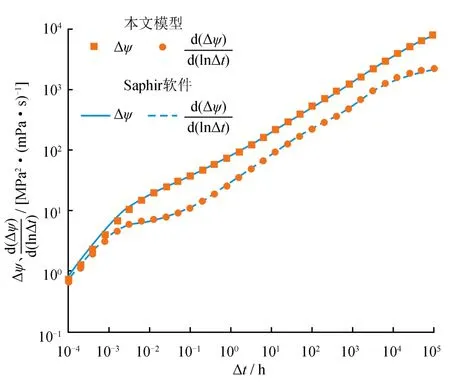
图3 本文模型与Saphir软件常规经典模型计算结果对比图
基于前述储层参数,考虑不同形态复杂缝网的影响,假设改造区长度为200 m,宽长比为0.3,主裂缝导流能力为500 mD·m,次裂缝导流能力为200 mD·m,支裂缝导流能力为100 mD·m,次裂缝密度为0.2 条/m,支裂缝密度为0.1 条/m,分别计算不同缝网形态下水平井试井曲线,并与常规单一裂缝水平井试井曲线进行对比。
复杂缝网下水平井试井曲线可以划分为4个流动阶段,如图4所示,分别为:①改造区拟径向流;②过渡流(或压裂段间未改造区径向流);③地层线性流;④系统径向流。与常规单一裂缝水平井试井曲线的主要区别是早期阶段单一裂缝模型的第一线性流特征被改造区拟径向流特征所取代。通过对比3种缝网形态下水平井的流动压力场,发现无论哪种缝网形态,在早期改造区均呈现椭圆形流动(拟径向流),如图5所示,该椭圆形流动区域形态的不同主要由裂缝导流能力的差异性所致。此外,3种缝网形态下水平井试井曲线特征基本一致,但双曲形缝网下压力导数曲线拟径向流阶段结束时间较早。这主要是由于双曲形缝网中间窄两端宽的分布不利于径向流的形成所致。

图4 复杂缝网下水平井试井曲线图

图5 水平井改造区早期流动地层压力分布图
由于改造区拟径向流的存在,使得复杂缝网下部分水平井压力导数曲线在过渡流阶段出现斜率大于1/2的情况,这是常规单一裂缝模型计算的水平井试井曲线所没有的特征,由此可以为压裂水平井实测压力导数曲线在非井筒储存阶段常出现斜率大于1/2的现象提供合理的解释,同时也可以作为判断水力压裂后是否产生复杂缝网的主要依据之一。
3.3 改造区大小的影响
与前述储层参数相同,考虑改造区大小的影响,在宽长比一定的条件下,改造区大小由改造区长度决定。以椭圆形缝网形态为例,宽长比为0.3的条件下,计算了改造区长度分别为50 m、100 m、200 m、300 m的水平井试井曲线。如图6所示,改造区越大,压力导数曲线拟径向流段持续的时间越长,压力导数水平线特征越明显;改造区较小时,由于压裂段间未改造区空间较大,过渡流阶段出现较明显的段间未改造区径向流特征。SRV越大,改造效果越好,气体渗流阻力越小。因此压力及压力导数曲线的值越小。
3.4 改造区宽长比的影响
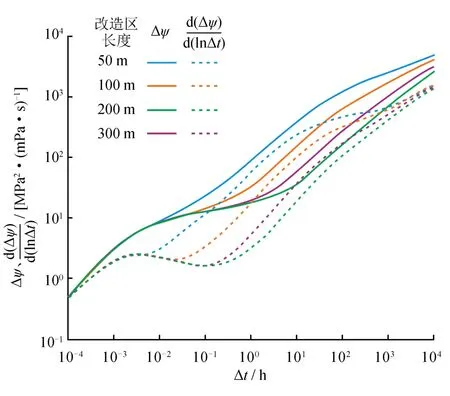
图6 不同改造区长度下水平井试井曲线图(宽长比为0.3)
以椭圆形缝网为例,在相同改造区面积下,计算了宽长比分别为0.1、0.2、0.4,对应改造区长度分别为245 m、173 m、122 m的水平井试井曲线。如图7所示,改造区越趋近长条形,即宽长比越小,改造区拟径向流段结束的时间越早,压力导数水平线特征越不明显,甚至改造区的拟径向流特征会被井筒储存效应掩盖,试井曲线特征越接近于单一裂缝模型,形成该现象的主要原因在于改造区越狭长,越不利于改造区内发生径向流动。另外,改造区越狭长,试井压力及压力导数曲线在后期的值越小,说明在相同的改造面积下,狭长形改造区有利于降低各段裂缝间的干扰。

图7 不同宽长比下水平井试井曲线图
3.5 改造区缝网密度的影响
计算了次裂缝密度分别为0.1 条/m、0.2 条/m、0.4条/m,支裂缝密度分别为0.05 条/m、0.10 条/m、0.20条/m的试井曲线,如图8所示,改造区缝网密度越大,井筒储存效应特征阶段结束得越早,改造区拟径向流特征出现得越早,压力导数水平线特征越明显,压力导数水平线值越小。
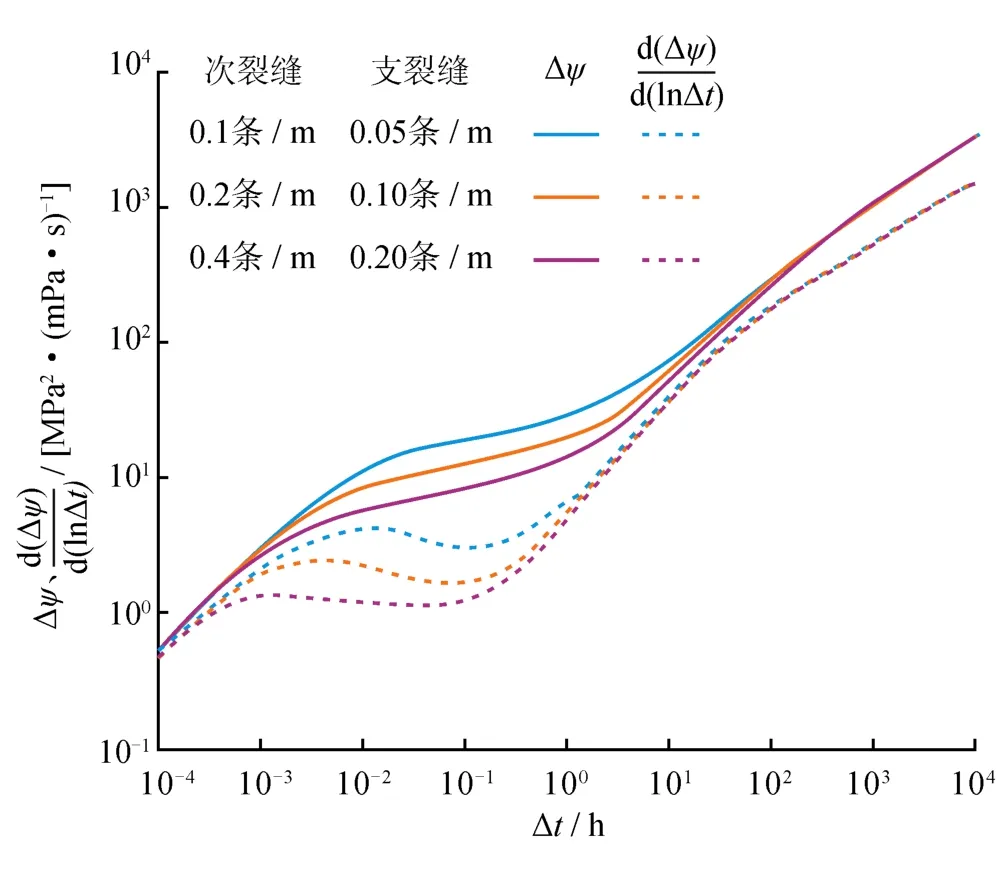
图8 不同缝网密度下水平井试井曲线图
3.6 改造区缝网导流能力的影响
如图9所示,缝网导流能力越强,改造区拟径向流段出现的时间越早,压力导数水平线值越小。缝网导流能力对试井曲线特征的影响与缝网密度的影响相似,因为两者皆是决定改造区渗流能力的参数。在实测曲线拟合过程中,由于缝网导流能力对试井曲线的影响与缝网密度的影响接近,容易造成解释结果存在多解性,此时应该综合考虑天然裂缝密度数据,使改造区缝网密度与天然裂缝密度基本一致,再调整缝网导流能力数据,从而降低多解性,获得较准确的缝网导流能力数值。

图9 不同缝网导流能力下水平井试井曲线图
4 实例应用
以鄂尔多斯盆地庆阳气田山1段致密气藏一口多段体积压裂水平井为例,该井水平段长1 100 m,原始地层压力为38.3 MPa,储层温度为124 ℃,孔隙度为6.4%,有效厚度为6.6 m,含气饱和度为73.9%,天然气相对密度为0.59,采用混合水压裂工艺进行体积压裂,压裂段数为10段。2017年8—10月进行了短期试采,累计产气量为218.5×104m3,整个测试过程可以分为3个阶段,第①阶段平均日产气量为30 203 m3,第②阶段平均日产气量为49 849 m3,第③阶段则为关井压力恢复阶段。分别采用本文所建立的复杂缝网渗流模型和常规单一裂缝模型进行解释,为了降低缝网模型试井解释的多解性,参考区域内同类型井的微地震监测结果来设定改造区宽长比的变化范围,参考该井体积压裂裂缝扩展模拟结果来设定裂缝导流能力的变化范围,根据该井储层天然裂缝密度来设定改造区缝网密度的初始值,然后在拟合过程中做一定程度的调整。
如图10、11所示,本文模型计算的理论曲线与实测曲线具有较好的一致性,而常规单一裂缝模型无论如何调整裂缝参数,均无法较好拟合实测曲线,主要原因在于常规模型压力导数曲线的斜率除了井筒储集与拟稳态阶段以外均小于或等于1/2,而该井实测压力导数曲线在井筒储存效应特征段结束后出现了斜率大于1/2的曲线,从而使常规单一裂缝模型无法拟合实测曲线。本质原因是该井体积压裂后储层中产生了复杂缝网,而非单一裂缝,所以,本文所建立的复杂缝网试井模型为解决这一问题提供了有效手段。如表1所示,通过该复杂缝网模型,不仅可以获取准确的储层参数,还可以获取改造区的大小及裂缝导流能力,为评价体积压裂改造效果及预测压后生产动态奠定了基础。

图10 现场多段体积压裂水平井试井双对数曲线拟合图
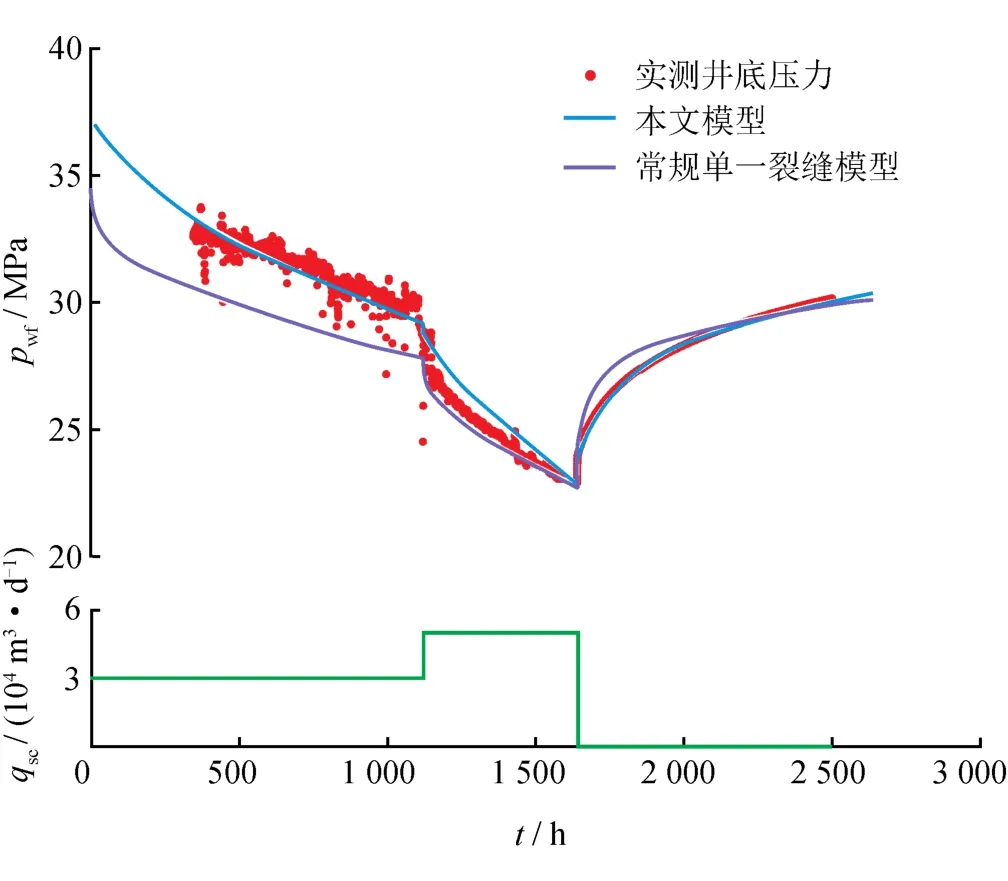
图11 现场多段体积压裂水平井测试期间压力拟合结果图

表1 庆阳气田山1段某多段体积压裂水平井试井解释结果数据表
5 结论
1)缝网模型与单一裂缝模型试井曲线的最大区别是在早期阶段,改造区拟径向流特征取代了第一线性流特征。
2)改造区拟径向流阶段结束的时间主要由改造区大小和形状决定。若改造区越大,改造区拟径向流阶段持续的时间则越长。若改造区形状越趋近于长条形,新模型试井曲线特征则越接近单一裂缝模型试井曲线的特征。
3)改造区拟径向流阶段的压力导数值主要由缝网导流能力和缝网密度决定。改造区缝网密度越大或者导流能力越大,井筒储存效应阶段结束得越早,改造区拟径向流压力导数值越小且水平线特征越明显。
4)庆阳气田致密气压裂水平井的实例分析结果证实了新模型可靠、实用,既可以获取准确的储层参数,又可以获取体积压裂有效改造区的大小及缝网导流能力。
