即时战略游戏的智能流场寻路算法设计与实现
2020-04-09张树美赵俊莉
李 恬,张树美,赵俊莉
(青岛大学数据科学与软件工程学院,山东青岛266071)
0 引言
游戏是在有限环境和固定规则中集中探索人工智能(Artificial Intelligence,AI)的理想领域,可以对解决问题的技术进行开发和评估以便解决更复杂的现实问题。人工智能多被应用在国际象棋、拼字游戏、西洋双陆棋、跳棋等棋盘游戏中[1],尤其是在最复杂的棋类游戏围棋中,AlphaGo 以绝对优势战胜了世界顶级职业围棋高手,证明了游戏中人工智能发展取得巨大突破。相应地,人工智能也被引入到了组成游戏的各种元素中,用以增加玩家的挑战性、游戏的可玩性和模拟世界的真实性,1986 年Minsky 提出了Agent 技术使得智能代理成为可能,2001 年Lent 将电子游戏用作人工智能研究的试验台,其后2003 年Buro 提倡进行即时战略(Real-Time Strategy,RTS)游戏的研究,并提供了一个用于探索游戏人工智能和许多其他核心复杂问题的沙盒。即时战略游戏作为人工智能应用最多最早的游戏之一,不仅有策略AI、战术AI、战术布置、危险估计和地形分析等多方面的AI 应用,更有包含简单AI 寻路和群体AI 寻路的路径搜索算法的重要应用。智能路径搜索算法是游戏中最基本最核心的问题,也是RTS 游戏中的重要部分。
路径搜索算法是在起点和终点之间寻找到一条可行路径的算法,应用在众多方面,包括网络流量、机器人路径规划、军事仿真和计算机游戏,有十分丰富的理论基础和众多应用场景。1956 年Dijkstra[2]提出的Dijkstra 算法是一种典型的最短路径算法,它计算图中某源点到其他某点的最短路径;其后1968 年Hart 等[3]提出了一种基于启发式搜索的A*算法,使得查找路径时间缩短;赵建民等[4]将A*算法应用到RTS游戏中,用以改进单个对象寻径;余帅等[5]将势场法运用到RTS 游戏的交互寻路中;叶青等[6]用双层朝向处理方法解决群体运动朝向;Malinowski 等[7]应用基于非易失性内存(Non-Volatile Random Access Memory,NVRAM)的分布式缓存实现了大规模的并行仿真;Sartoretti等[8]结合强化和模仿学习提出了一种多智能体寻路(Multi-Agent Path Finding,MAPF)的新框架,Ho等[9]采用批处理的方法实现无人机交通管理中的多智能体寻路。但是,这些寻路算法并不能满足多智能体快速寻路的需求,目前大多是通过优化单条路径规划速度来提高整体运动速率,并没有在全局宏观改进群体路径规划,所以需要新的算法用来解决短时间内大量移动智能体的并发寻路问题。在2013 年由Pentheny 提出的流场寻路算法[10]将物理学中的流场动力学引入到游戏寻路中并成功应用于游戏《最高指挥官2》和《坚守阵地2》中,实现了多物体的同时快速寻路,突破了智能体数量的限制,使游戏中的智能体可以模拟人的真实行动,移动时能够聚集和分散。
本文主要设计了即时战略游戏中一种新型的路径搜索算法——流场寻路算法,并对算法从数据结构存储、路径代价计算和流场生成算法三方面做出了改进,进一步提高了流场寻路算法的运行效率,解决即时战略游戏中的碰撞阻塞问题。
1 问题描述
1.1 RTS游戏中的寻路问题
即时战略游戏[5]是一种即时进行的,有资源采集、基地建造、科技发展和战斗元素的战略游戏。即时战略游戏历史悠久,在英国最早可追溯到1983 年Gibson 开发的《Stonkers》和1987 年发行的《Nether Earth》,在北美普遍认为1984 年由Evryware’s Dave 和Barry Murry 开 发 的《The Ancient Art of War》是现代即时战略的始祖[11]。大型的即时战略类游戏可以让人体验到一种指挥千军万马纵横沙场的英雄意境,如:《帝国时代》、《星际争霸》和《红色警戒》[12]。以上游戏都充分利用AI加强对资源建筑控制和战斗冲突,使得在游戏中更加注重移动规模、即时性和交互性[13-15],但以上的这几款典型RTS 游戏都或多或少存在多次碰撞和行动阻塞的缺点[16],为解决此类问题,《星际争霸》采取取消碰撞[17],《红色警戒》按顺序物体逐一进行寻路,《帝国时代》采用限制寻路数量等的简化方法。为了让游戏中的智能体寻路更加真实和精细,游戏开发者必须使用智能化的搜索路径方法,这样游戏才可能最大限度地模拟真实世界的场景,游戏中的移动智能体就像真正的人一样,能够针对不同的情景做出合理适当的反馈,做出感知环境后的最有利的行为。
随着计算机技术的发展、网络传输效率的提高和游戏品质的提升,RTS 游戏的地图、场景、声音和角色造型也都有不同水平的进步,所以地图和游戏智能体规模增大使得游戏中智能寻路越来越重要[18],采取一种智能寻路算法可以避免游戏中的阻塞现象和多次碰撞问题,不同的算法所呈现出的效果不尽相同,适用场景也不同。
1.2 常见寻路算法局限性
游戏中的地图一般采用栅格化的方法来构造以便于路径计算,然后采用不同的寻路算法进行计算。图1 为200×160大小的矩形地图,将其划分为多个长度为4 的小正方形,则网格的个数为50×40,将每个网格看作节点,边则为节点间的通路,将(0,0)设置为目标节点,深灰色区域表示障碍物,是不可通过区域。初始化地图完成后,随机生成n 个智能体,使用不同的寻路算法计算每个智能体的生成路径。
最早所采用的寻路算法为Dijkstra 算法,它被广泛应用于各种场合,如:地理信息系统(Geographic Information System,GIS)路径规划[19]、城市道路优化[20]、物流配送[21]、救灾路线[22],可以看出以上场景都是两点间寻找一条最优路径的问题,只需考虑找到两点之间的最短路径,忽略了实际问题中全局群体移动和出口瓶颈的阻塞碰撞问题,并不适用于游戏中即时不确定的多个智能体移动。其后,A*算法的出现解决了游戏中单个非玩家角色(Non-Player Character,NPC)的智能化寻路问题,如减少了搜索区域,降低搜索的成本时间,确保在较短的时间内找到相对合适的最优路径,成为目前游戏中使用最广泛的寻路算法,同时也在城市交通[23]、车辆调度[24]、镶嵌线提取[25]、停车场寻路[26]、士兵作战[27]中有重要应用。

图1 初始化地图Fig.1 Initialization of map
人工势场法作为一种常见的局部路径规划方法也被引入到RTS游戏中,其算法主要是模拟虚拟力场,目标点对物体产生引力,障碍物对物体产生斥力,引力和斥力产生的合力形成物体的运动路径。如遗传算法、蚁群算法等智能仿生算法也常常被应用在路径规划中,主要是模拟遗传变异、蚂蚁觅食等自然界中的各种行为和现象,但是此类智能算法需要多次迭代才能得到更为准确的路径。
以上方法都可实现路径规划,但传统路径规划计算速度慢,人工势场法适用于局部规划,智能路径规划需多次迭代,这都十分影响游戏的流畅度和用户体验。而流场寻路算法很好地解决了RTS 游戏对于寻路时间和数量的要求,适合于大规模模拟人群的移动,其主要思想是根据地图和目的地生成有关于路径的“场”,这个“场”标记了地图中任意位置到达目标节点的运动方向,本文将详细介绍流场寻路算法。
2 流场寻路算法
2.1 基本数据结构
流场寻路有三种数据类型,用来存储经过某节点代价时的代价字段类型,存储该节点到达目标节点最小代价值的完整代价字段类型和经过该节点时到目标节点方向的流场字段类型。
代价字段类型是初始化地图时对每个节点的代价提前设定数值的代价类型,一般用最大值代表不可通过的区域,如:墙体、高山等,用正整数代表通过的代价值,并用不同的值代表不同的地形地貌,如:沼泽、海洋、沙漠和斜坡代价值大于经过平原的代价值,代价值最小为1。如果有某些地方没有明确的代价值,则将一个静态全局变量赋给代价字段以便于流场的计算和表示,本文实验的初始代价值为20,用变量INFI表示最大值268 435 455(0xFFFFFFF),以大小为10×10 的部分地图为例,结果如图2所示。
完整代价字段存储的是完整代价值和标志位的字段类型,完整代价值是当前节点到目标节点的代价值,标志位记录整合代价的活动波前和视线,以便优化流场字段的方向值。图3 中深灰色代表的是障碍物,黑色直线是从点G 所发出的视线,即点G与障碍物最近边缘的连线并延长所形成的射线,而视线的方向和两视线间的所夹部分是由障碍物和点G的位置来决定的。最浅灰色部分代表的是视线所穿过的区域,作用是将中等深灰色部分的智能体移动到此区域以便在视线范围内,可直接到达目标点G。
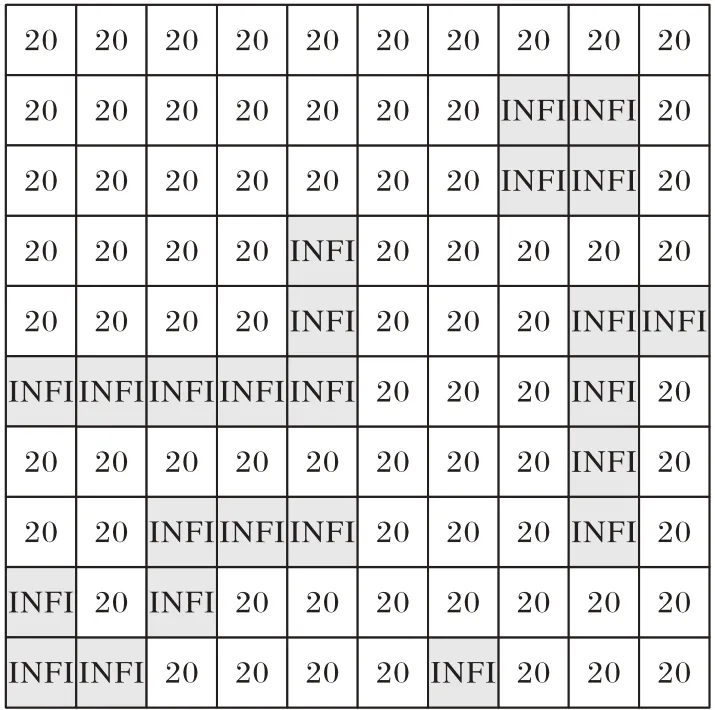
图2 代价字段示意图Fig.2 Schematic diagram of cost field
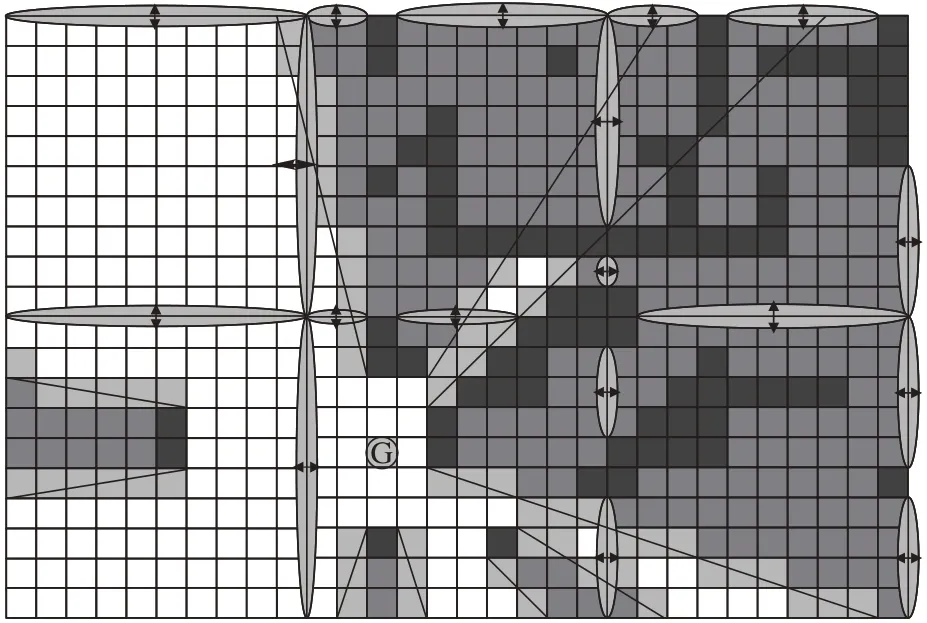
图3 完整代价字段示意图Fig.3 Schematic diagram of integration cost field
流场字段存储一个枚举方向查找表的索引字段类型,智能体到达目标节点过程中经过某一节点时的运动方向,一般会是枚举类型,有东、西、南、北、东南、西南、东北、西北这八个枚举值。如果检测到到达方向的下一节点为障碍点,则跳过该节点,如图4 所示,遇到障碍时不可跨越,所以只能向箭头所指的六个方向移动。
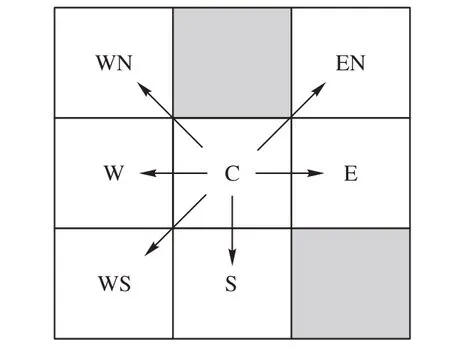
图4 流场字段示意图Fig.4 Schematic diagram of flow field
2.2 算法基本思想
即时战略游戏中一般将地图划分为多个正方形组成的规则网格,网格点看作节点,寻路在网格的基础上进行搜索。流场寻路只需要计算一次地图中所有节点的流场方向就可以不受智能体数量的限制进行移动。
算法的基本步骤如下:
1)初始化智能体和地图,定义集合S,地图中绘制网格、障碍和目标节点,集合S 用来存放已经计算过但未确定流场方向的节点;
2)将目标节点v加入集合S,并赋值v的完整代价值为0;
3)从集合S中选取完整代价值最小的节点u;
4)记录节点u,并将其从集合S中删除;
5)计算更新节点u 的8 邻域节点的完整代价值,并将未加入集合S的节点加入集合S;
6)根据完整代价值确定8邻域节点流场字段值;
7)重复上述3)~6)过程,直至集合S为空。
通过循环得到集合S 中节点的邻域节点的代价值,将代价值进行比较决定经过节点后的下一节点是8 邻域节点中的哪个节点,并进行标记,生成流场字段值,表明每个运动智能体经过此节点时的流场方向。
以上就是流场寻路的数据结构和整个算法思想,虽然流场寻路算法解决了多智能体同时快速寻路的问题,让RTS 游戏中的所有运动智能体看起来十分流畅和智能,但是,流场寻路算法仍有不足,如:算法运算过程中产生不必要的重复计算,数据没有一个很好的排列方式和计算顺序,计算地图中代价值的方法和得到流场的方法比较复杂甚至需要计算非线性偏微分方程,本文就这些问题对流场寻路算法做了一定改进。
3 流场寻路算法的改进
3.1 数据存储方式
2.2 节算法基本步骤中的3)、4)中,节点u 并非随意选择的节点,应选取在集合S 中完整代价值最小的节点,最简单方法为遍历整个集合并进行比较。但随着地图的增大,比较次数也会增多,并且比较次数与地图增大次数呈正线性相关,其比例关系如图5所示。
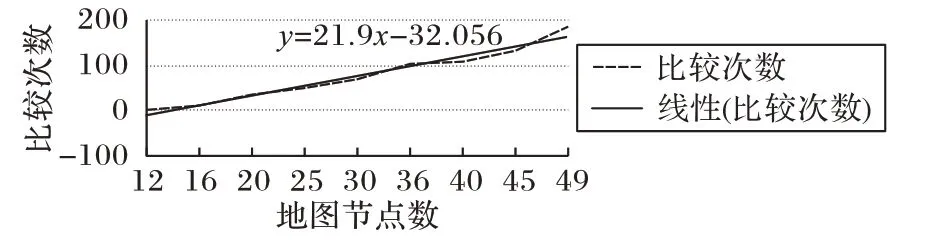
图5 地图节点数与比较次数的关系Fig.5 Relationship between number of map nodes and number of comparisons
如图6 所示,采用红黑树方式进行节点的存储,保证前序遍历的第一个节点是完整代价值最小的节点,每次取最小元素进行循环即可。虽然这会造成排序插入的消耗,但是红黑树的查找、插入和删除的时间复杂度均为O(log n),因此在大地图、多次进行比较的情况下对于算法优化的效果十分明显。
将OPEN表和CLOSE表引入算法中,OPEN表中存放将要计算的节点,初始只有目标节点,CLOSE表中存放已经计算过并得到流场的节点,OPEN 表采用红黑树的方式进行存储,按照完整代价值排列,前序遍历为代价值最小的元素。
遍历的基本过程为:取OPEN 表的代价值最小的元素节点,将其加入到CLOSE 表中,并检查该节点的相邻节点,其中相邻节点分为三种:
1)如果该节点均不在OPEN 表和CLOSE 表中,将其加入到OPEN 表中,并对该节点的整合代价值和流场方向进行赋值;
2)如果该节点在CLOSE表中,新生成的整合代价值小于原来的值,则节点重新赋值;
3)如果该节点在CLOSE表中,新生成的整合代价值大于等于原来的值,不做任何操作。
如图7 所示,深色圆点部分是已经遍历过CLOSE 表中的节点,浅灰色是OPEN 表中的节点,未标记部分则是还未遍历过的节点。
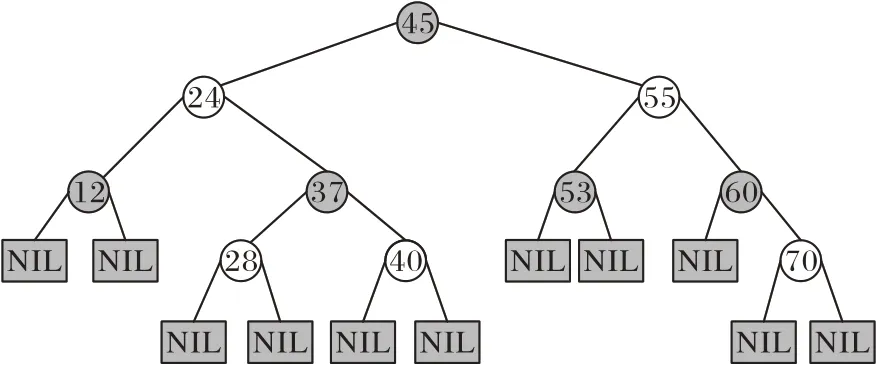
图6 红黑树结构Fig.6 Red-black tree structure
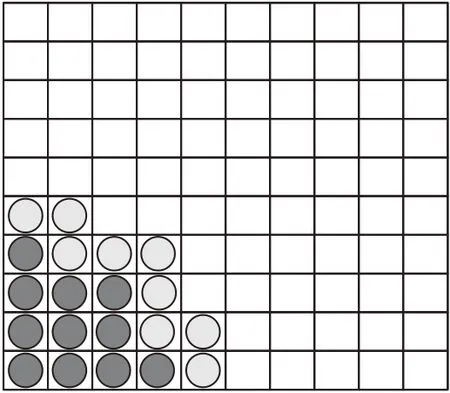
图7 节点的遍历过程Fig.7 Traversal process of nodes
3.2 利用惩罚函数优化路径代价计算
在Pentheny 提出的代价值的计算方式中,采用程函方程[28]进行计算,程函方程是一种非线性偏微分方程,以哈密顿-雅可比偏微分方程(Hamiltonian-Jacobi partial differential equation,HJ-PDE)[29]的形式进行定义,如式(1)所示:
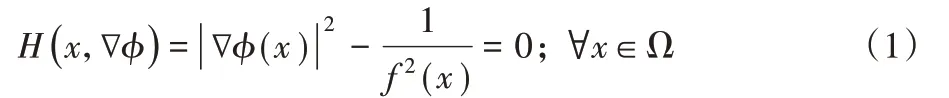
其中:Ω 是Rn中的域,φ(x)是到源点的距离或者时间,f(x)是在Ω 中定义的正向速度函数。通常用n 元数组来定义节点,以二维节点x=(i,j)为例,本文算法定义直接连接两个节点的线段作为边,边的长度沿对应的轴p(p ∈{x,y})来定义网格的长度hp,将相邻邻域节点定义为单边相连的节点,如有节点y=(i+hx,j),则是节点x=(i,j)在x 轴方向的相邻邻域节点。采用Godunov逆风离散化[30]对程函方程进行离散,在x方向的离散结果为g(x),如式(2)所示:

U(x)是节点x=(i,j)指向φ 方向的离散化近似值,是沿着p 方向U(x)相邻两个邻域的最小U 值,(n)+=max(0,n)。由以上分析可知,基于密哈顿-雅可比的程函方程的约束条件为:,并得到坐标轴的每个方向都将影响整合代价值的计算结果。当n 取得更小值时,g(x)取值随之减小,因此,在整合代价值计算过程中尽量避免方向的变化,对在x、y两个方向发生变化的g(x)进行惩罚。
在计算完整代价值的时候需要重复计算,由于非线性偏微分方程的计算比较复杂,又有和(n)+=max(0,n)
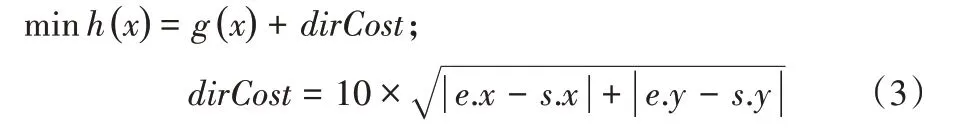
根据实验结果,选择惩罚因子为10 对方向进行惩罚,保证对角线方向的代价值大于水平或竖直方向。
3.3 流场计算
流场寻路的基本算法中采用视线法预处理数据并进行整合代价值的计算,但是在“波”向前进行推动的时候,需要比较所有计算过的到达此节点的完整代价值,并保证值的最小唯一性,这就造成计算过程中节点信息存储的增加。受文献[31]启发引入Dijkstra算法,采用广度遍历的方式反向进行计算,根据前置邻接点和后置邻接点解决多路径的问题,使得计算过程中同时计算多条路径,进而得到最优解。
将目标节点看作是初始节点,在“波”向前推进的过程中,运用Dijkstra算法计算每个节点的前置邻接点,这在流场中的方向将有前置邻接点指向这个节点,具体实现过程为:两个约束条件,将求解有约束的非线性规划问题转换为计算无约束极小值问题,根据问题实际情况采用惩罚函数进行计算,再进行整合代价值的计算。
将约束问题min g(x),满足限制ci(x)≥0,∀x ∈I,转化为无约束问题序列,如式(3)所示:
1) while(OPEN表不为空)
2) {
3) 取OPEN表代价值最小的节点;
4) 将节点删除并插入到CLOSE表中;
5) 更新当前点周围的节点到OPEN表;//周围8邻域的节点进行遍历更新
6) 确定周围节点的前置邻接点是否为当前节点;
7) 确定周围节点的流场方向;
8) }
将目标节点首先加入红黑树中,采用广度优先的搜索方式,将目标节点的相邻节点全部加入到树中,借助改进后的存储方式,每次取完整代价值最小的点进行计算,计算后删除当前节点,选取下一整合代价值最小的点,循环操作直到树为空。
图8 为截取部分所得完整代价数值表,左下角为目标节点(0,0)。生成流场结果如图9所示。
完成流场计算后,智能体运动将不受数量限制,处于地图中任意位置的智能体均可按照流场方向移动,且在大地图中多智能体移动时更符合群体移动规律,智能体倾向于向地势平缓更易到达目标点的空旷区域聚集移动。
本实验从数据存储方式、路径代价计算方法和流场计算方式三个方面改进了流场寻路算法。改进后的流场寻路算法在数据读取方面更具有优势,并且简化了算法的计算步骤,不再需要计算视线后再得到整合代价值才能计算出流场方向,可通过直接计算整合代价值得到前置邻接点的方式得到流场方向。本文采用的方式简化了算法的实现过程,提高了路径的计算速度,从整体上优化算法。
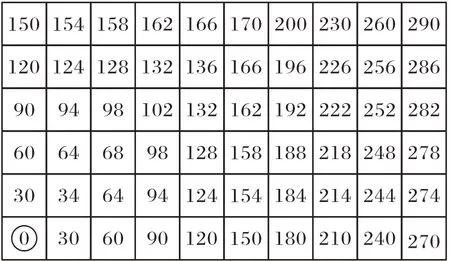
图8 节点的完整代价值Fig.8 Integration cost value of node

图9 流场结果图Fig.9 Result diagram of flow field
4 实验结果与分析
仿真实验在Visual Studio 2017 平台下使用OpenGL 实现算法可视化,对不同数量的智能体,对不同算法生成路径和完成移动的时间进行比较。实验结果表明,流场寻路在即时战略游戏中的作用十分显著,使大量移动智能体在更短的时间内到达同一目的地。
实验中分别比较了Dijkstra 算法、A*算法、人工势场法、流场寻路和改进后的流场寻路算法中移动智能体数量为1、10、20、50、100和200情况下的寻路时间和完成移动时间。实验数据证明,当移动数量越多时,采用流场寻路算法更具有优势,能在相同时间内无数量限制进行寻路。
表1 为不同算法不同数量智能体计算路径所需要的时间,而表2 为不同算法下不同数量智能体完成移动所需时间。结合表1、2 中的数据可以说明,流场寻路算法在大型地图的多次寻路中具有优势,并在障碍较多、地形复杂的地图中也可以快速寻路,具有较好的稳定性。
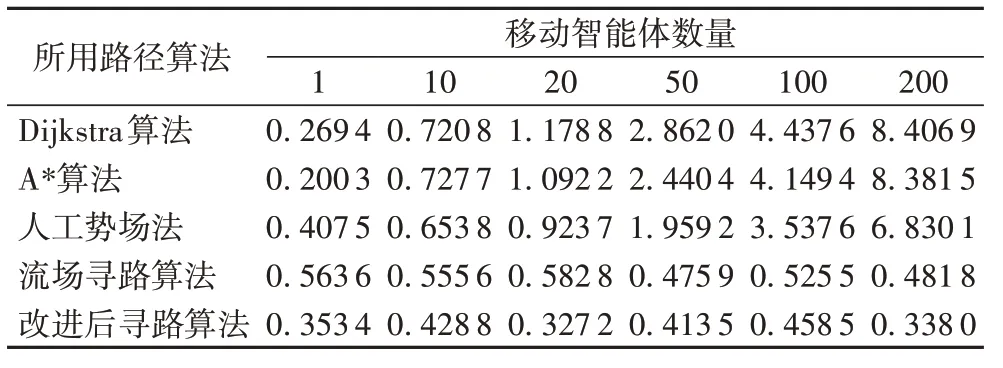
表1 不同算法的平均寻路时间 单位:sTab.1 Average pathfinding times of different algorithms unit:s
通过表1、2 也可以看出,随着移动智能体数量增多,传统算法的所用时间约为数量的倍数,而流场寻路算法不会随着数量的增多而增加寻路时间和运动时间,是一个在一定数值范围内的稳定值,寻路时间约为0.4 s,移动时间约为20 s。因为地图中有x×y个节点,类比于n个节点中的Dijkstra 算法时间复杂度为O(n2),则本文中的Dijkstra 算法时间复杂度为O((m×n)2);又因为智能体的数量为MOVE_OBJECT_NUM(以u来代替),需执行u次Dijkstra算法,可以得到整个结果的时间复杂度为O(u×(m×n)2);如果使用流场寻路的话,则只需计算一次算法,为O((m×n)2)。
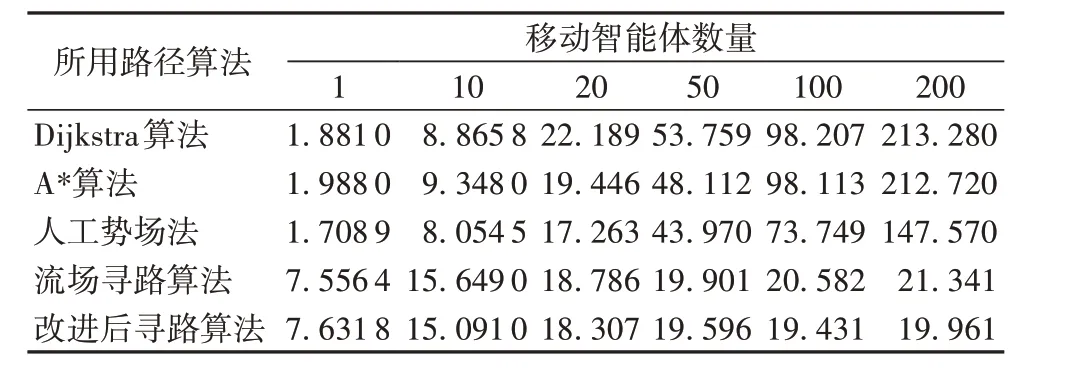
表2 不同算法的平均移动时间 单位:sTab.2 Average moving times of different algorithms unit:s
5 结语
大量游戏[32]如早期的沙丘、红警再到星际、魔兽以及现在的帝国时代、最高指挥官等都需要解决类似多智能体移动的问题,本文提出了流场寻路算法,并对其在数据存储方式、整合代价值计算方式和流场生成方式进行组合式改进,提高了流场寻路的计算速度和智能体的移动效率,也提高了游戏的智能水平,使得数以万计的智能体也可在大型地图上同时并发寻路,增加了该类游戏的可玩性和真实性,进一步优化了游戏体验。
本文主要集中在改进算法本身并实现,该算法还可实现多目标点的流场计算,也可用图形处理器(Graphics Processing Unit,GPU)代替中央处理器(Central Processing Unit,CPU)进行计算。对于移动中躲避障碍物、墙壁和其他智能体等问题,后续将进行深入研究。
