最小化具有无线携能通信的全双工中继系统发射功率和

周叶宁，李陶深，曾 敏，肖 楠

（广西大学计算机与电子信息学院，南宁530004）

0 引言

基于射频（Radio Frequency，RF）信号的信息传输和能量捕获技术已经成为在新一代无线通信网络中传输数据和提供电能的替代方法。在无线网络中基于射频信号，采用无线携能通信（Simultaneous Wireless Information and Power Transmission，SWIPT）技术来传输携带信息波和能量波的RF 信号的实现也已取得最新的进展［1-2］。基于无线通信传输系统，在文献［3-6］中对实现SWIPT的时间切换（Time Switching，TS）和功率分配（Power Splitting，PS）的实际接收机结构进行了描述，该接收机可以对接收的RF 信号分别进行信息解码（Information Decoding，ID）和能量捕获（Energy Harvest，EH）。其中，在文献［4］中提出使用多天线和协调多点系统来减少路径损耗并提高系统效率，而在能量受限的半双工（Half-Duplex，HD）中继系统中应用SWIPT技术也开始被考虑［5-6］。

最近，关于在无线传输网络应用自能量回收的技术已成为众多研究者的研究对象。将自能量回收技术应用在点对点无线通信系统和无线中继系统中都有了初步的探索，能量受限的节点仅利用从接入点捕获的专有能量和自回收能量进行数据传输［7-10］。其中，在文献［9-10］中考虑了联合发射波束成形和接收功率分配设计在下行链路中采用SWIPT 的多用户广播系统，并提出用非凸优化的二阶锥规划松弛方法来解决联合优化问题。

在最新的研究中，一种具有自能量回收的无线供电全双工（Full-Duplex，FD）放大转发（Amplify-and-Forward，AF）中继系统被提出［11-13］，并采用了一种新颖的两阶段传输协议。在文献［12］中，考虑了具有自能量回收的双向传输FD点对点系统，并通过应用半定松弛（Semi-Determined Relaxation，SDR）解决给出信噪比（Signal-to-Noise Ratio，SNR）和捕获能量约束的非凸问题。具有自能量回收的FD 无线中继系统的安全波束成形也得到了深入研究［14-17］。而在全双工中继系统中结合应用SWIPT 和自能量回收则是一个新的研究方向和挑战。

本文提出一种采用SWIPT 技术且具有自能量回收功能的双向传输全双工中继系统，在该中继系统中采用AF传输协议，中继利用SWIPT 技术传输RF 信号到目的节点，能量受限的目的节点采用功率分配方案分别进行ID 和EH。由于绝对全双工和双向传输模式，使得中继与目的节点可以通过环路信道捕获部分自回收的能量。本文以优化系统发射功率和为目标函数，但不包括优化源节点发射功率。应用SDR 和秩松弛方法将原始难以求解的非凸问题转换为较易于求解的半定规划问题，并应用拉格朗日方法求解的最优解表达式。若半定规划问题存在秩1 解，则原始优化问题的最优解与SDR 问题的最优解等同［12］。通过仿真实验结果表明，与传统的没有采用SWIPT 技术的具有自能量回收的双向传输中继系统相比，本文方案可以获得更有效的系统性能增益。

本文使用符号如下：粗体小写和大写字母分别表示向量和矩阵；CM×N表示M×N复矩阵，复矩阵的厄密共轭、转置、轨迹和秩分别用(⋅)H、(⋅)T、Tr(⋅)和Rank(⋅)表示；‖‖⋅ 和 ||

⋅分别表示复数向量的欧几里得范数和复数标量的绝对值；(⋅)-≻0 表示矩阵是半正定的；IN表示一个N×N 单位矩阵；具有零均值和方差σ2的对称复高斯随机变量的分布定义为∼CN(0，σ2)。

1 系统模型与问题描述

在现有的多接收多发射天线的源节点和单接收单发射天线的点对点全双工系统基础上，提出采用无线携能通信技术的双向传输全双工中继系统结构如图1 所示。该系统配置有M 根接收天线和N 根发射天线的中继（R），而源节点（S）和目的节点（D）由一根接收天线和一根发射天线组成。在下行链路中，R 从S 接收RF 信号并将检测到的信息放大转发到D；同时在上行链路中，R 将从D 接收到的反馈信息协作传输到S。在R 到D 的下行链路传输过程中采用SWIPT 技术，S 和R 与R和D 之间分别有双向传输的信息流，从R 到D 只有单向能量流。中继和目的节点通过从环路信道自回收能量，将产生的有害自干扰转换为可回收的有益可用能量，并且还可以节省中继的电能，也无需额外的硬件配置或其他方法去消除自干扰。

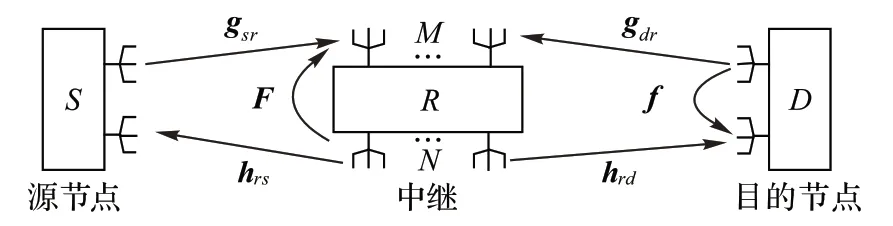
图1 具有SWIPT的全双工中继系统Fig.1 Full-duplex relay system with SWIPT

本文系统的全双工中继工作的逻辑结构如图2 所示，中继接收器同时接收来自S 和D 的信息，接收信号通过中继处理，再同时发送到S 和D，能量捕获器用于捕获中继环路信道的能量。

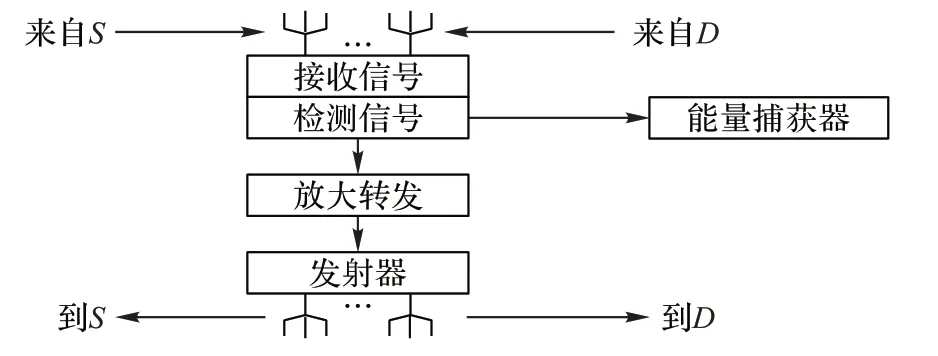
图2 全双工中继的逻辑结构Fig.2 Logical structure of full-duplex relay system

根据已有研究提出的PS 方案将接收的RF 信号分成信息流和能量流，其中以ρ 的功率分配比用于ID，以1-ρ 的功率分配比用于EH［11］。本文在能量受限的D 处设置功率分配器进行ID 和EH，其中被捕获的能量被转换成电能并存储在可充电电池中，接收的信息通过信息发送器传输，具有自能量回收的目的节点的结构如图3所示。

图3 具有自能量回收的目的节点的结构Fig.3 Structure of destination node with self-energy recycling

假设所有的信道都是准静态衰落信道，且信道状态信息已知［17-18］，为了计算简洁将时隙块标准化。从S 到R 和R 到D的下行链路信道分别用gdr∈CM×1和hrs∈CN×1表示；D到R和R 到S 的上行链路信道分别用gdr∈CM×1和hrs∈CN×1表示；在中继和目的节点处的环路信道用F ∈CM×N和f ∈C1×1分别表示。忽略时间延迟τ，认为S 与D 发送到R 的信号是同时的，则R接收到的信号可表达为：

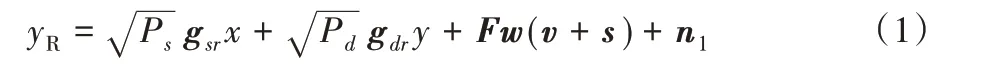
其中：Ps和x ∼CN(0，1)与Pd和y ∼CN(0，1)分别是在S到R 与在D 到R 的发射功率和发射标记符号；Fw(v+s)+n1是环路信道产生的自干扰信号，w ∈CN×1是中继发射波束成形向量，s ∼CN(0，1)和v ∼CN(0，1)分别表示在R 到S 和在R 到D 的发射标记符号，是在中继处的天线噪声。

在D处接收到的信号为：

其中n2是在D 接收器处具有零均值和方差的加性高斯白噪声（Additive White Gaussian Noise，AWGN）。由于采用功率分配比为ρ ∈(0，1)的PS方案，将接收的信号yD分为信息流y IDD和能量流，则它们的表达式分别为：

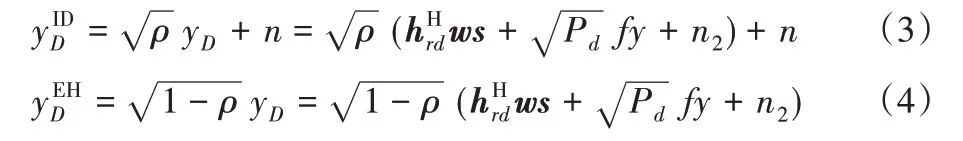
在自干扰完全消除后的接收信号为

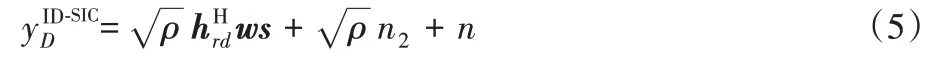
其中n ∼CN(0，σ2)是在D处进行ID后额外引入的噪声。则在S处接收的信号表示为：

其中，n3是在S 接收器处具有零均值和方差为的AWGN噪声。

忽略噪声n2携带的能量，用0 ＜η ＜1表示能量转换效率，则由能量受限的目的节点在每个时隙块中捕获的总能量为：

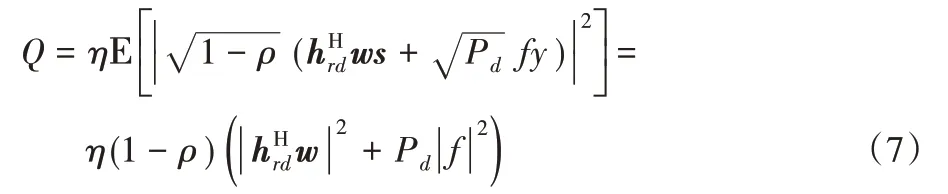
忽略自干扰信号，在R处的信噪比为：

在D与S处的SNR分别为：

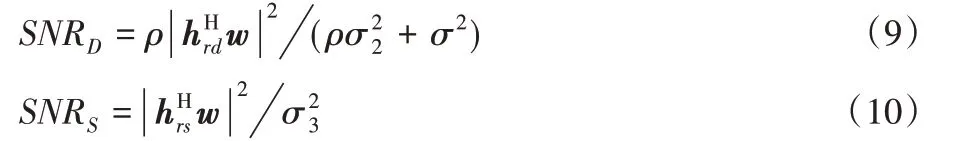
2 问题描述及求解

假设源节点以向中继传输数据所需的最小发射功率进行传输，在中继系统采用AF协议，忽略时间延迟τ。为了延长D的寿命，设置能量目标值ε，在D 处捕获的总能量应该高于给定的能量目标值，且在D 处的发射功率应该低于ε。同时，为了保证系统的传输效率和性能，S、R 和D 的每个SNR 应该高于给定的阈值，分别用γs、γr和γd表示［12］。由于在S 处的发射功率不受限，放宽在S处的SNR 约束条件，则系统发射功率和的优化问题P可描述如下：

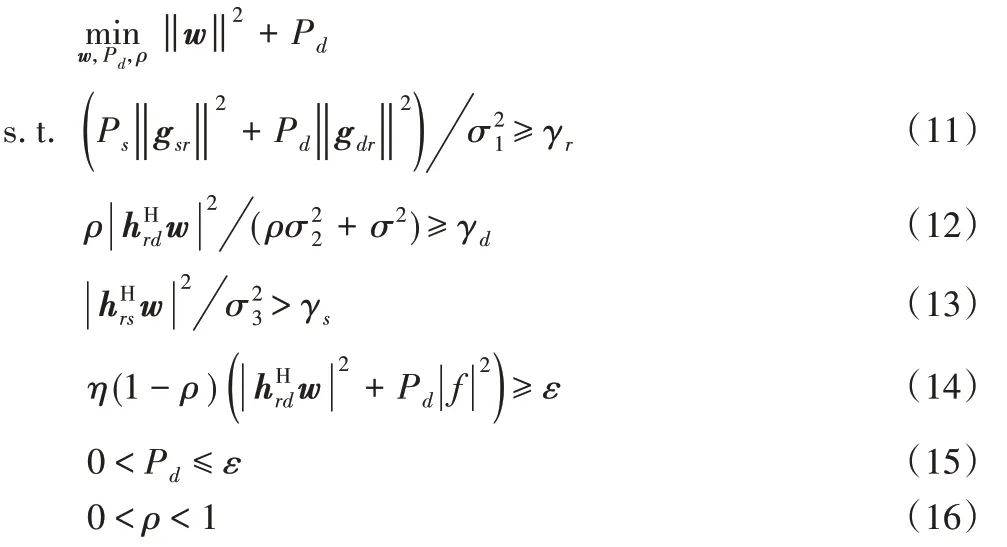
由于原始问题是非凸的，采用半定规划方案来解决原始优化问题。定义和Hrs=都是秩1 矩阵，由于问题矩阵的秩1 约束是非凸且难以求解的，因此丢弃矩阵秩约束条件，再应用SDR 将非凸问题转换为更易求解的凸优化问题［12］。则半定松弛问题P-SDR描述如下：

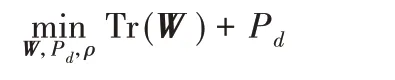
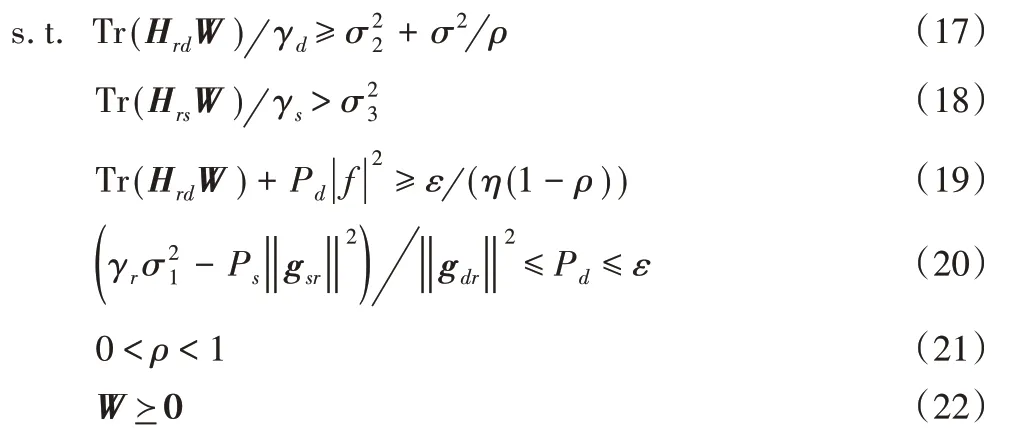
显然，P-SDR 问题可以通过现有的优化软件求解得到最优解。若半定规划问题的最佳波束成形矩阵W*满足Rank(W*)=1，则原始问题P的最优解等价于问题P-SDR［12］的最优解。

本文利用拉格朗日方法求解不等式约束优化，并根据约束优化的KKT 条件设置拉格朗日函数［20-22］。为每个约束定义拉格朗日乘数变量λ1≥0，λ2≥0，λ3≥0，λ4≥0，λ5≥0 和Φ ≥0，则问题P-SDR对应的拉格朗日函数为：

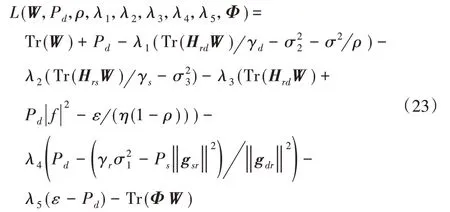
则对应的拉格朗日对偶函数为：

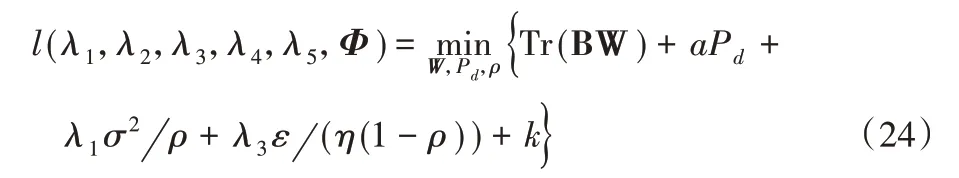
则有：

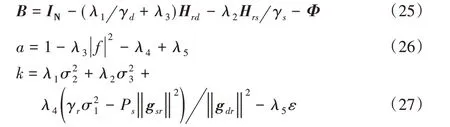
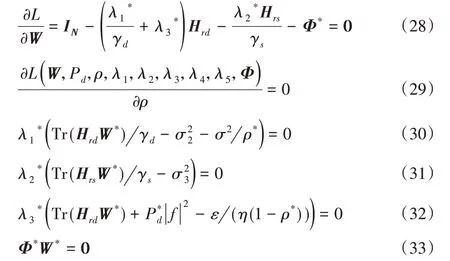
这里只列出必要的KKT 条件等式。由式（29）可以求解得功率分配比率和拉格朗日变量最优解ρ*和Φ*的等式：

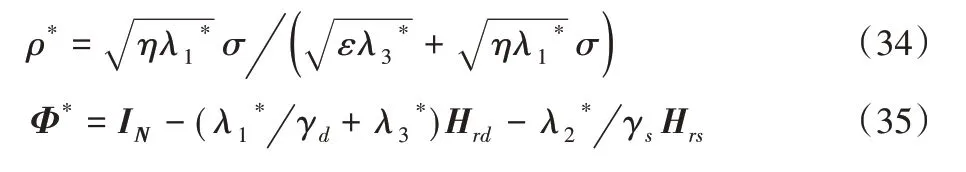
由拉格朗日对偶互补松弛的特性，可以推导出约束等式（30）和（32）在最优点处满足：

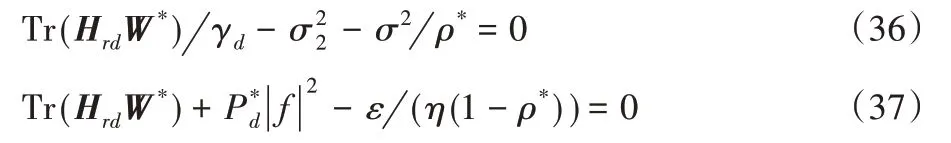
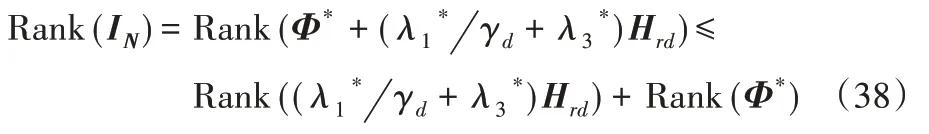
且由于中继发射波束成形矩阵满足Rank(W*)=1，因此原始问题P 与问题P-SDR 同解，而从以上结论可以推导得出问题P-SDR的最优解。

3 传统双向传输中继系统

在传统的双向传输全双工中继系统中，假设中继配置有M+N 根天线，源节点和目的节点都配置一根发射天线和一根接收天线。与本文系统不同的是系统的总传输时间块T 分别被分成两个传输时隙T/2，如图4 所示。在第一阶段，S 向R发送信息，同时R 向D 发射RF 信号；在第二阶段在D 将反馈信息发送到R 的同时R 放大转发信息到S。此外，该系统不具有自能量回收的功能，其他假设条件与所提系统相同。

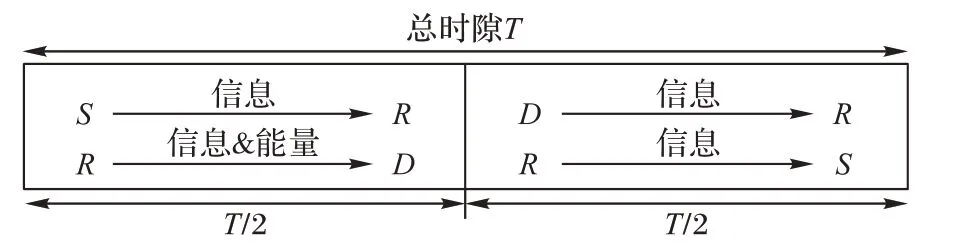
图4 传统全双工中继传输协议Fig.4 Traditional full-duplex relay transmission protocol

第一阶段，在R和D处接收的信号为：

其中nr1、nr2是在R处具有零均值方差为的AWGN。

第二阶段，在R和S处接收的信号为：

yd被功率分配器分为两个流为：

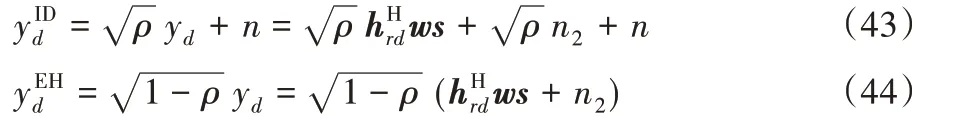
因此，在D处捕获的总能量表达式为：

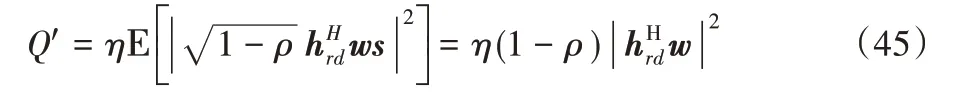
忽略时间延迟，假设第一阶段和第二阶段在中继处的发射功率相同。则优化问题P0可以描述如下：

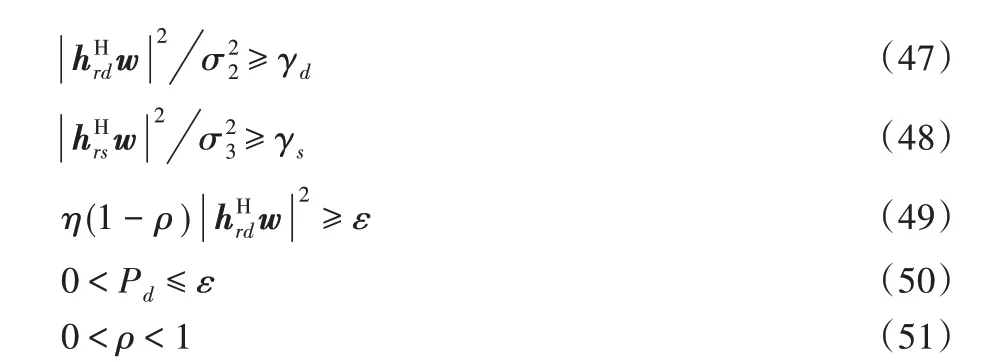
因此，丢弃秩约束，采用SDR 方案将P0 转换为P0-SDR，具体描述如下：

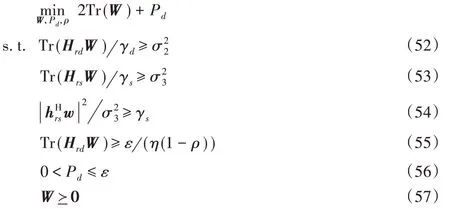
显然，问题P0-SDR是一个能由优化软件求解的凸优化问题，其详细的基本求解方法及原理与原始问题P 相似，因此省略对问题P0求解过程的赘述。

4 模拟实验与分析

本章将根据模拟实验结果来评估并分析本文系统的性能。假设系统带宽为10 MHz，在所有的模拟实验中，设置dBm，σ2=-50 dBm 和η=0.5，使用瑞利衰落来模拟系统中S 和D 之间的信道，并且S 和D 之间每间隔5 m信号衰减设置为40 dBm［10］。信道描述为：

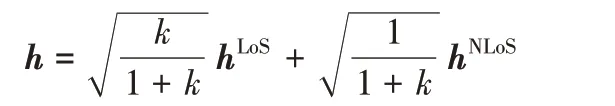
为了探究源发射功率对优化问题的数值结果的影响程度，设置ε 为-10 dBm，-5 dBm，0 dBm，5 dBm，10 dBm，Ps从0 dBm 扫描到30 dBm。如图5 所示，当源发射功率Ps值在不同的ε下变化时，系统发射功率和的优化目标值保持稳定值，这表明优化目标不受Ps变化的影响。这是因为在发射功率不受限的源节点和中继之间仅传输信息，能量变化发生在中继和目的节点之间。该数值结果验证了本文系统的可靠性。在后面的模拟实验中都设置Ps=15 dBm。

为了探索在目的节点处的速率-能量平衡时最小化系统发射功率的最佳功率分配比ρ*，并验证本文提出的求解方法的优化性，实验模拟了在不同的ε 下发射功率和随ρ 变化的情况。设置ε为-6 dBm，-3 dBm，0 dBm，3 dBm，6 dBm，ρ从-45 dBm扫描到-1 dB。模拟结果如图6 所示，在固定的不同ε 下，发射功率和随着ρ 的增加稳定且缓慢地增大，并且其全局最小值处的相应横坐标点是ρ 的最佳值，且关于ρ*的一次函数直线对应于固定ε 下的最优值聚合点，验证了本文方案的较优性。

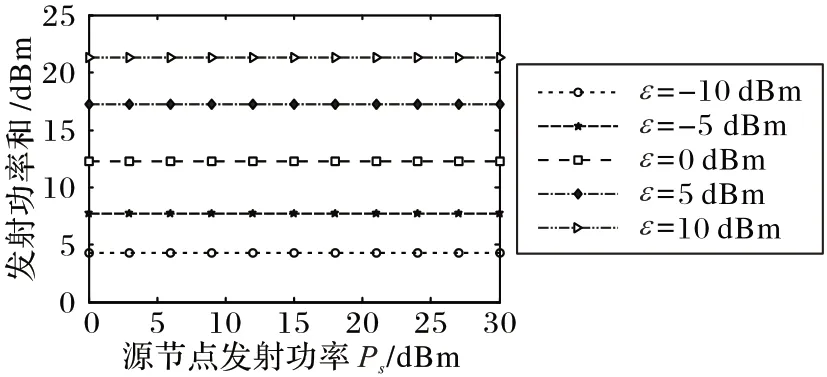
图5 在不同ε下的发射功率和与Ps的关系Fig.5 Relationship between transmit power sum and Ps under different ε

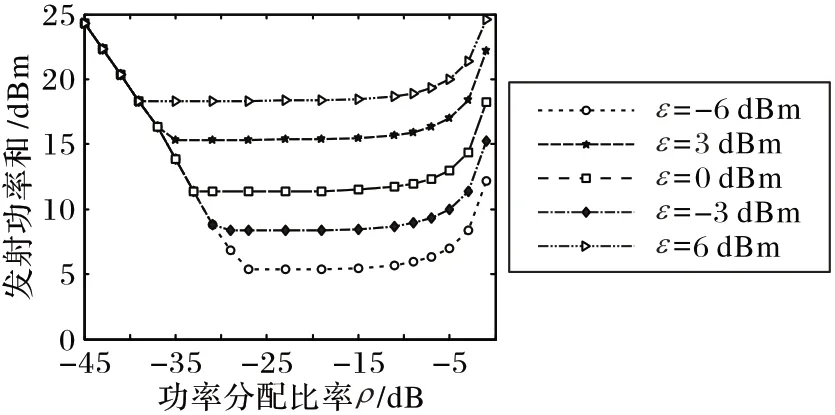
图6 在不同ε下的发射功率和与ρ的关系Fig.6 Relationship between transmit power sum and ρ with different ε

接下来，为了探讨在能量约束下从目的节点处发射功率的变化趋势，实验模拟了在不同的ε 下运行100 次优化程序，观察目的节点发射功率的变化。将ε 分别设置为-10 dBm，-5 dBm，0 dBm，5 dBm，10 dBm。如图7 所示，可知目的节点的发射功率值初始时在能量目标值上下略有波动，其后随着运行次数的增加，在目的节点处的发射功率趋于稳定，甚至等于给定的能量阈值。当运行次数足够多时，Pd的最优解可以表示为，通过将该方程代入优化问题求解，可得到功率分配比最优值ρ*和最优波束形成向量w*。

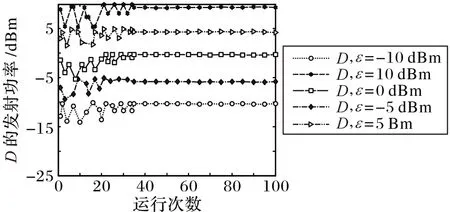
图7 在不同ε下随运行次数变化的目的节点的发射功率Fig.7 Transmit power of destination node varying with the number of runs under different ε

为了比较本文系统与传统双向传输系统的性能，实验模拟了在给定不等同SNR 阈值下通过扫描能量目标值来观察系统发射功率和变化。分别给出γd=γs=γr=10，15，20 dB，同时能量目标阈值ε从-10 dBm扫描到5 dBm，在不同SNR和能量阈值下两个系统的发射功率和变化如图8所示（Proposed表示本文方案，Traditional 表示传统方案）。可知随着ε 的增大，系统发射功率和的值开始缓慢增加，然后呈线性增加；而且，本文系统的上升速率小于传统系统的增长速率，这是由于传输时隙间隙降低了传统系统的双向传输效率，以致需要比本文系统更高的功率传输。另一方面，是由于本文系统消除了自干扰的不利影响，并且在中继和目标节点处利用自能量回收为系统增加了额外的可供电能。

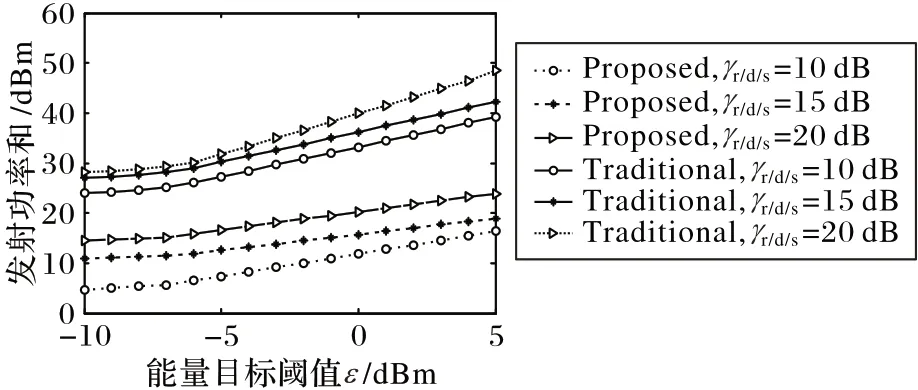
图8 不同SNR时ε对本文系统与传统系统的发射功率和的影响Fig.8 Impact of ε on transmit power sum of proposed and traditional system under different SNR

最后，研究了在本文系统与传统双向传输系统下，中继发射天线数量N 对系统发射功率和增益的影响。如图9 所示，根据固定不同的能量目标阈值ε 为-6 dBm，0 dBm，6 dBm，并设置M=4，中继发射天线的数量N 分别设置为2、4、8、12、16、20、24、28、32。从图9中可以看出，系统发射功率和随着N增加而逐渐降低，这是因为随着发射天线的数量增加而获得的发射天线波束形成矩阵的增益增大。此外，可知本文系统的发射功率和与传统系统的相比较低，这是由于本文系统的中继的自能量回收消除了自干扰并节省了功率。

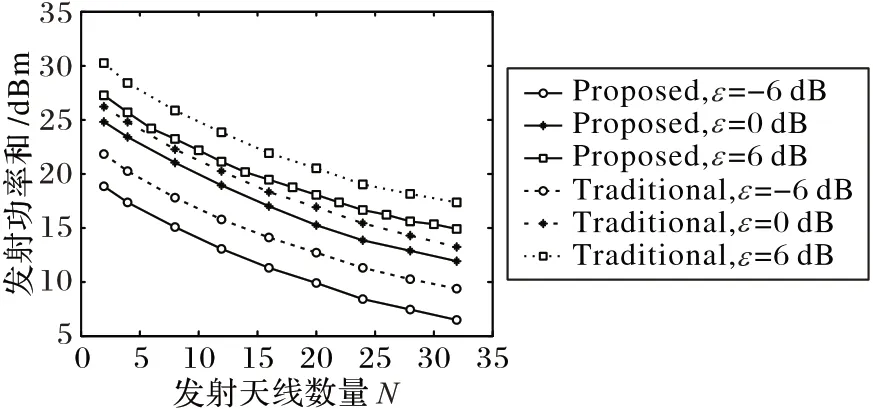
图9 发射天线数量N对系统发射功率和的影响Fig.9 Impact of the number of transmit antennas N on system transmit transmission sum

5 结语

本文提出了一种应用无线携能通信（SWIPT）技术的具有自能量回收的双向传输全双工中继系统，其中继和目的节点都能从环路信道回收自能量，系统的信息传输、能量捕获和协作传输在一个时间块中同步进行；并且给出了全双工中继工作模式的逻辑结构和能量受限的目的节点的物理结构。本文将最小化系统发射功率和作为优化目标，还联合优化了中继发射波束成形向量、目的节点发射功率和功率分配率，应用SDR 和秩松弛技术将原始非凸问题转换为凸优化问题，结合半定规划和拉格朗日方法来求解优化问题的最优解。实验仿真对比了本文系统与传统双向传输中继系统，结果验证了利用自能量回收不仅可以消除自干扰，而且可以显著优化系统发射功率和，且由于SWIPT 技术与全双工中继系统的结合，使得本文系统比传统的双向传输系统具有更高的性能增益。