基于神经网络的车辆抗冲击防护组件优化*
2020-04-09李明星王显会周云波孙晓旺胡文海
李明星,王显会,周云波,孙晓旺,曾 斌,胡文海
(1. 南京理工大学机械工程学院,江苏 南京 210094;2. 东风汽车公司技术中心,湖北 武汉 430056)
在目前反恐战争和未来武装冲突中,军用高机动车辆面临主要威胁形态为非对称威胁,其中最具代表性的是地雷简易爆炸装置(improvised explosive device, IED)[1],提供可以对付IED 威胁的轻型高机动车辆成为部队的最新需求。如何提高军用高机动车辆防护能力以保障车内乘员安全,已经成为多学科交叉前沿研究课题[2],目前主要采用V 型结构来提高军用车辆底部抗爆炸能力。而防护组件的设计需要根据具体车型的特性来匹配,同时随着防护要求的不断提高,防护组件的设计面临越来越多的挑战。
Kendale 等[3]结合实验和仿真分析,对不同的车体形状下乘员的损伤进行研究。结果表明,底部为V 型结构的车体具有偏置爆炸冲击波的作用,能够有效减小爆炸冲击作用力,从而降低乘员损伤风险。张中英等[4]在兼顾其通过性与防护能力时,通过仿真分析研究得出V 型角度取值为140°最合适。不过V 型车身底部结构的最大不足之处是车身的离地距离较大,使得车辆的操纵性降低。目前国内发展较快的军用高机动车辆,其防护组件的选取很少直接采用V 型底部结构。含蜂窝夹层的V 型底部复合装甲是近几年的研究成果,不仅存在V 型结构偏置爆炸冲击能量,而且装甲内部的蜂窝组件还存在一定的吸能作用。孙京帅[5]分析了在面内冲击载荷作用下,蜂窝材料变形机制与其相应的能量吸收性能,并分析了蜂窝单元几何尺寸对蜂窝吸能、质量及比吸能的影响。目前相关学者对防护组件性能的研究多局限于对其某个特性进行分析改进,对防护组件的整体设计进行分析研究的相对较少。
针对目前对防护组件设计研究的局限性,本文中对防护组件整体性能优化进行了大量的仿真分析工作与实验验证。传统的防护组件设计需要通过大量的实验与有限元仿真的配合,有经验的工程师也需要通过大量的计算先获得仿真结果较好的模型后,再通过实验验证最终确定设计方案。近年来,随着优化理论的发展,神经网络和遗传算法在结构优化设计中得到越来越广泛的应用。Feng[6]提出一种基于粒子群优化的RBF 神经网络优化算法,可以提高整个神经网络的性能。柳建容等[7]基于神经网络遗传算法对减震器进行仿真分析,获得了较好的优化结果。本文中以实验为基础,结合有限元分析得到的数据,同时利用神经网络和遗传算法对防护组件进行优化设计。
1 抗冲击组件爆炸模拟与实验
1.1 抗冲击组件模型描述
基于某型车的防护组件初步设计方案如图1 所示。防护组件整体采用螺栓连接,其面板与背板之间填充蜂窝铝,两侧有限位钢板。此时防护组件面板背板厚度均为6 mm,板内横梁厚度为4 mm。防护组件长1 800 mm、宽1 500 mm。防护组件面板距地面450 mm。梁采用BS700 钢,面板及背板采用6252 装甲钢。
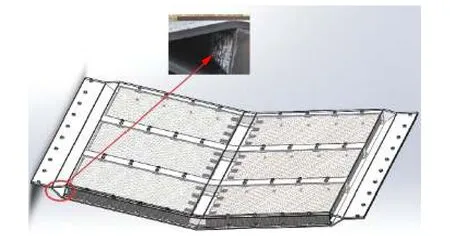
图1 防护组件结构图Fig. 1 Structure of protective component
1.2 抗冲击组件爆炸仿真理论
有限元模型如图2 所示,为确保仿真与实验模型的一致性,在配重块上增加了质量单元对整个模型进行配重处理,使仿真模型质量与实验模型质量一致。除此之外,在有限元模型中还建立了空气、土壤和炸药模型。装甲材料为高强钢,在有限元中采用LS-DYNA 中3 号材料模型*MAT_PLASTIC_KINEMATIC:
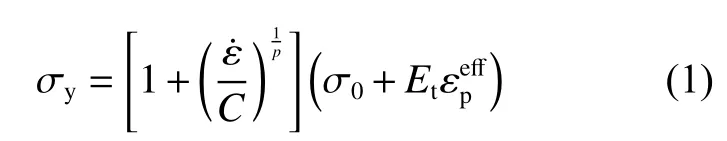
式中:σy为初始屈服极限,Et为硬化模量,为应变率,C 和p 为应变率参数。LS-DYNA 中包含高能燃烧模型(CJ)和点火生成模型(ZND),因为ZND 模型的炸药参数缺少实验支撑,所以仿真中一般使用CJ 模型。CJ 模型中的Jones-Wilkins-Lee(JWL)方程是半经验状态方程,其压力、体积和内能之间的关系为:
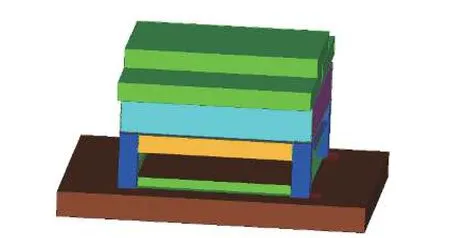
图2 台架仿真有限元模型Fig. 2 Bench simulation finite element model
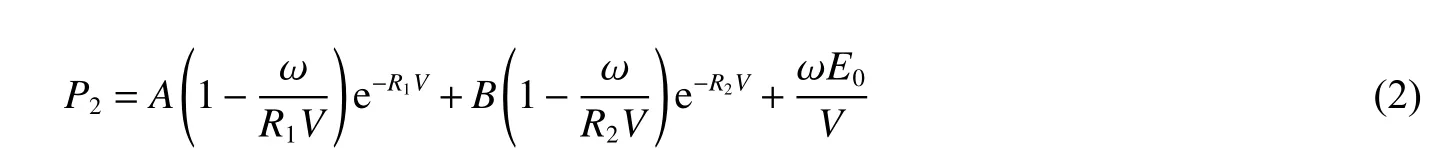
式中:P2为压力,E0为初始内能密度,为相对体积,A、B、R1、R2、ω 为材料常数,状态方程中的参数见表1[8]。

表1 TNT 炸药的JWL 方程参数Table 1 JWL equation parameters of TNT explosives
1.3 抗冲击组件台架实验
实验时防护组件上方放置一块平钢板以模拟整车中的地板变形。将防护组件安装在台架上,并用质地均匀的配重块以整车的质量进行配重实验。实验则按AEP-55 标准的2b 等级进行,即将6 kg 当量的TNT 放在防护组件下方任意位置进行爆炸实验,本次实验选取具有代表性的正下方进行爆炸验证。爆炸实验后上板、中间铝结构、底板分离,连接螺栓全部断裂;边缘及面板均有弯曲变形;中间铝结构部分被压溃至极限。爆炸后模拟整车地板的钢板发生很大程度的弯曲变形,变形量达210 mm,钢板整体呈上凸状,钢板表面出现多处凹坑,其中一侧边缘部分受压变形,出现裂纹。
由爆炸实验的结果来看,初步设计的防护组件无法满足AEP-55 法规的2b 实验要求。防护组件在6 kg 当量TNT 的爆炸冲击下解体,模拟整车底板的变形量未能符合小于150 mm 变形量的设计要求。因此需要在此实验的基础上对防护组件进行优化,直到其满足设计要求。图3 所示为数值仿真与实验中防护组件的压溃变形情况。

图3 数值仿真与实验中的抗爆组件压溃情况Fig. 3 The crushing situation of anti-explosion components in numerical simulation and experiment
通过仿真与实验的对比,可以看出仿真分析与实验结果有较好的一致性,为后续的仿真分析与优化工作奠定了基础。产品设计过程需要采用各种优化方法,不能单独依靠数学规划的优化手段。由于防雷板组件相对复杂,单纯的依赖最优化方法是难以做到的,应结合目前国内外设计经验尽可能采用V 型结构。鉴于给定的设计空间,该防护组件最大V 型角度能达到160°。在此基础上通过优化设计改变面板背板材料、改变面板与背板之间梁的布置,以提高防护组件的整体防护性能。
2 抗冲击组件多响应参数优化
2.1 优化数学模型构建
提高防护组件的整体防雷效果可以通过调整面板、背板和加强梁的相关参数匹配,实现防雷组件整体性能的优化。同时可以通过优化软件的灵敏度分析,确定各个设计变量中对优化目标效果较明显的设计因子。在防护组件抗冲击性能优化设计中,设计变量如图4 所示,选取5 个尺寸变量、2 个形状变量,其位置如图5 所示,初始值及其取值范围如表2 所示,变量X1~X5为厚度变量,此处对变量X6、X7作简要说明:在Hypermes 的tool 面板下选择HyperMorph 工具,对要需要变形的网格进行处理。首先创建变形域,如图5 所示,然后选择相应的变形指令,本文中研究中间横梁在防护组件之间的布局对防护组件整体性能的影响,所以对横梁的变形操纵为沿x 方向的移动。前后移动量各取200 mm,然后对变形的节点信息输出节点信息文件,且其变量范围为操纵时输出变量数据的百分比。在优化工具Hyperstudy 中通过调用相应节点文件来生成变量。在防护组件结构设计中,防雷板变形位移量D 与防雷板总体质量M 最小化,该优化问题的数学模型为:
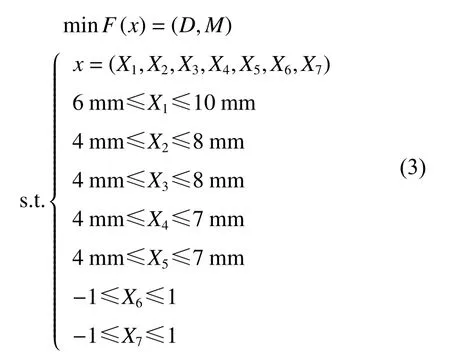
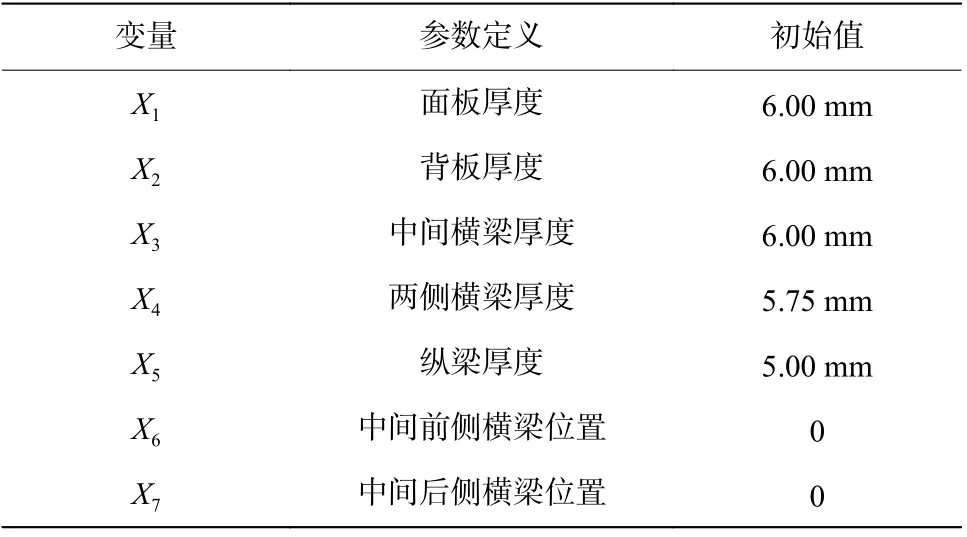
表2 设计变量初始值Table 2 Design variable initial value
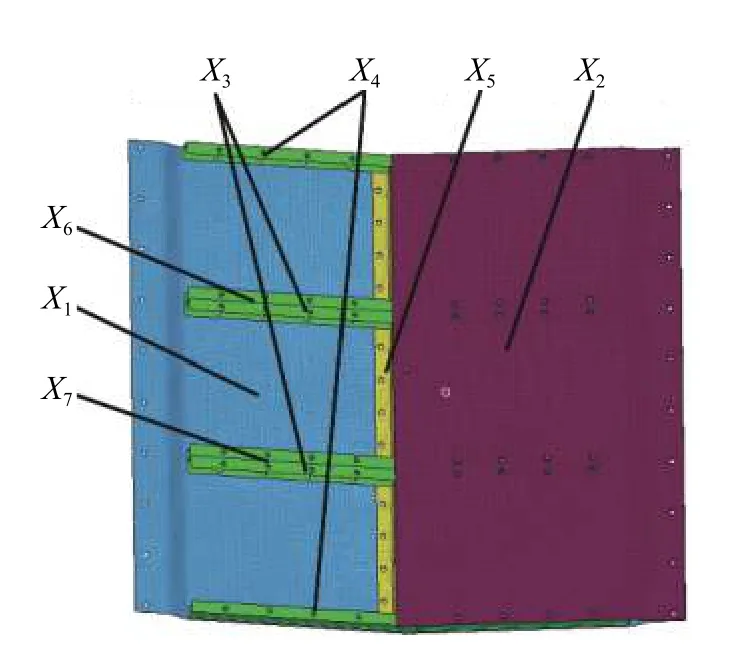
图4 设计变量位置示意图Fig. 4 Design variable position diagram
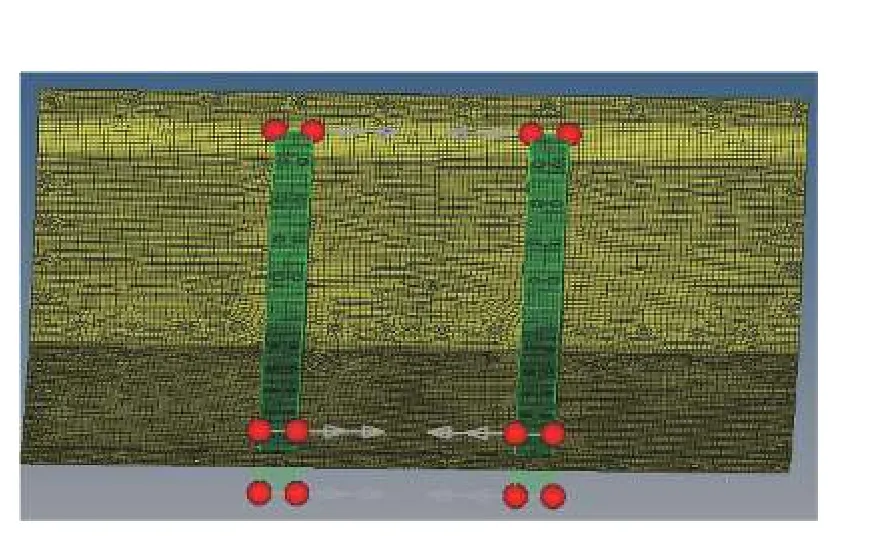
图5 变形域图Fig. 5 Deformation domain diagram
2.2 抗冲击组件参数影响分析
常用的实验设计方法有:中心组合设计(CCD)、Box-Behnken 设计、拉丁超立方设计等。CCD 应用二次多项式预测其对评价指标的影响,优点为实验少、设计简单且有较好的预测能力。Box-Behnken 设计方法具有近似旋转对称性,避免了极端点的出现,缺点是该设计方法只能包含3~21 个因子。拉丁超立方实验设计具有效率高和采用均衡性好等优点[9]。由于研究对象的高度非线性,具有空间随机填充能力的拉丁超立方实验设计,较CCD、Box-Behnken 设计具有用同样的点数可以研究更多组合的优点。为了获得具有全局意义的神经网络模型,利用拉丁超立方实验方法对7 个设计变量进行采点,共有40 组样本点。样本的因素及水平情况如表3 所示。
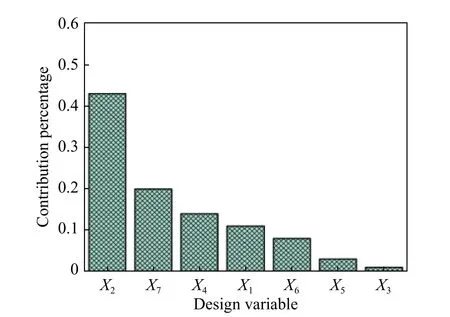
图6 设计变量贡献率Fig. 6 Design variable contribution rate
结合方差灵敏度分析[10](ANOVA)方法分析了7 个设计变量对防护组件变形位移响应量的贡献率,如图6 所示,设计目标在满足质量要求的前提下其防护组件的位移量要尽可能小,所以灵敏度分析只需观察各设计变量对输出变量位移量的贡献量。由分析可知,X3即中间横梁厚度与X5纵梁厚度对防雷板变形位移量的影响极小,所以在后续数值优化中将剔除这两个设计变量。
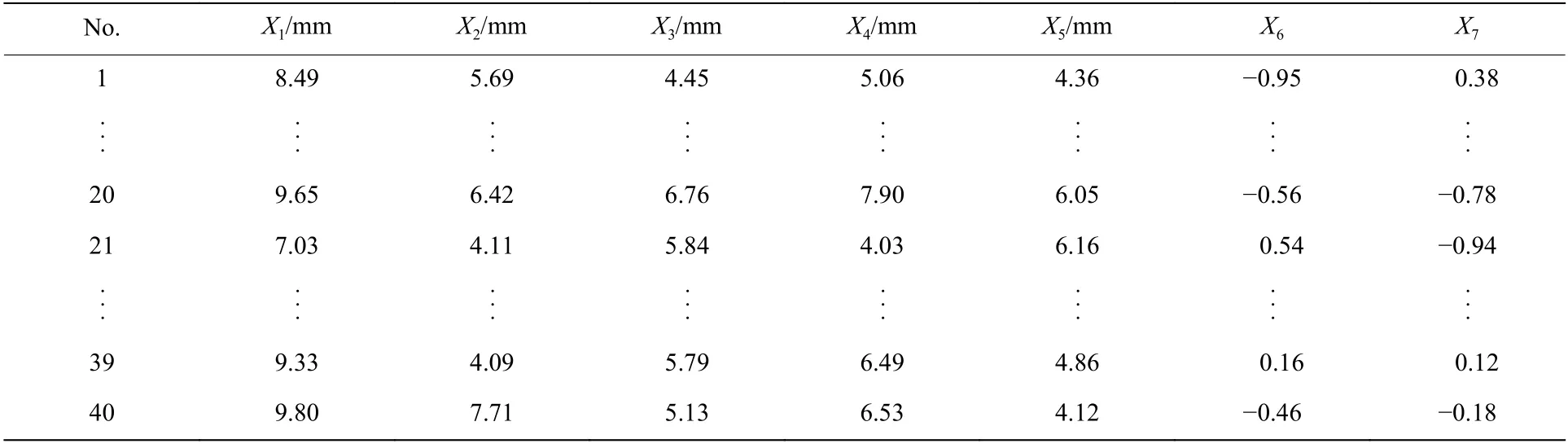
表3 拉丁超立方实验采样样本Table 3 Latin hypercube test sample
2.3 神经网络响应面构建
将拉丁超立方实验样本得到的有限元分析数据用于拟合近似模型。基于近似模型进行的优化设计的优势在于:将复杂的工程优化问题转换为数学寻优问题,可以极大地减小工作量。主流近似模型有Kriging 模型、神经网络模型等。Kriging 以变异函数理论和结构分析为基础,其某未观测点表达式为:

式中:λi为待定加权系数。λi应满足两个条件:
(1)无偏估计,设估值点的真值为y(x0)。因模型空间的变异性,y(xi)以及和y(x0)可视作随机变量,即为无偏估计:
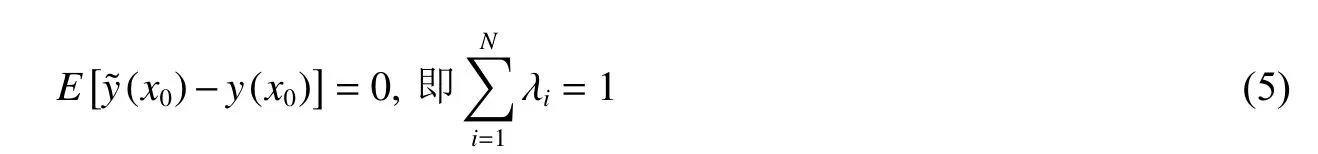
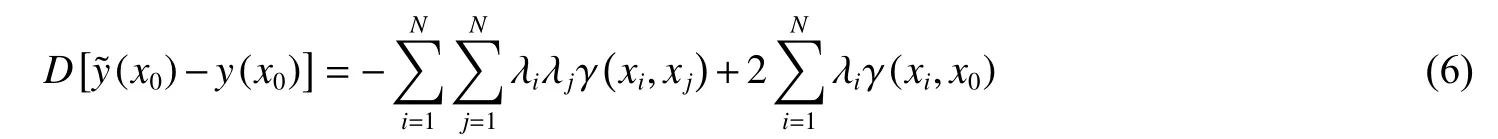
式中:γ(xi,xj)表示以xi和xj两点的距离作为间距h 时参数的半方差值。Kriging 常用的核函数为高斯函数与指数函数。在拟合设计变量多且高非线性的工程问题中,Kriging 模型存在较大误差。
神经网络近似模型有径向基函数(RBF)神经网络,和椭圆基函数(EBF)神经网络。将优化变量作为输入层,响应目标作为输出层,隐含层由激活函数构建的神经元组成。RBF 神经网络通常以高斯函数作为激活函数,对任意输入x 的输出层中第k 个神经元可以表达为:

径向基函数神经网络由于其简单的拓扑结构和全局逼近能力在信号处理[11]与非线性系统建模和控制等方面得到了广泛的应用[12]。神经网络结构优化方法有很多。进化算法是基于生物进化原理的一种搜索算法,有较好的鲁棒性与全局搜索能力,凑式法通过训练与比较不同的RBF 神经网络结构来实现,但时长较长[13-16]。相对而言进化算法更适合防护组件设计优化的匹配。防护组件的设计变量与其动态响应参数之间是一种高度非线性映射关系,对于复杂系统两者之间很难用函数关系显示表达。而神经网络有极强的非线性映射功能,非常适用于建立这种复杂的非线性模型[17]。图7 为神经网络和Kriging模型拟合的响应面,可以看出,由于Kriging 采用无偏估计尽可能平滑的接近样本点,当非线性程度非常高时,拟合存在较大差异。而神经网络代理模型对于高度非线性问题具有更好的拟合效果。因此本文中采用神经网络模型作为后续数学优化的基础。图8 为主影响因子X2与X1、X4、X6和X7四个因子拟合的位移响应面。
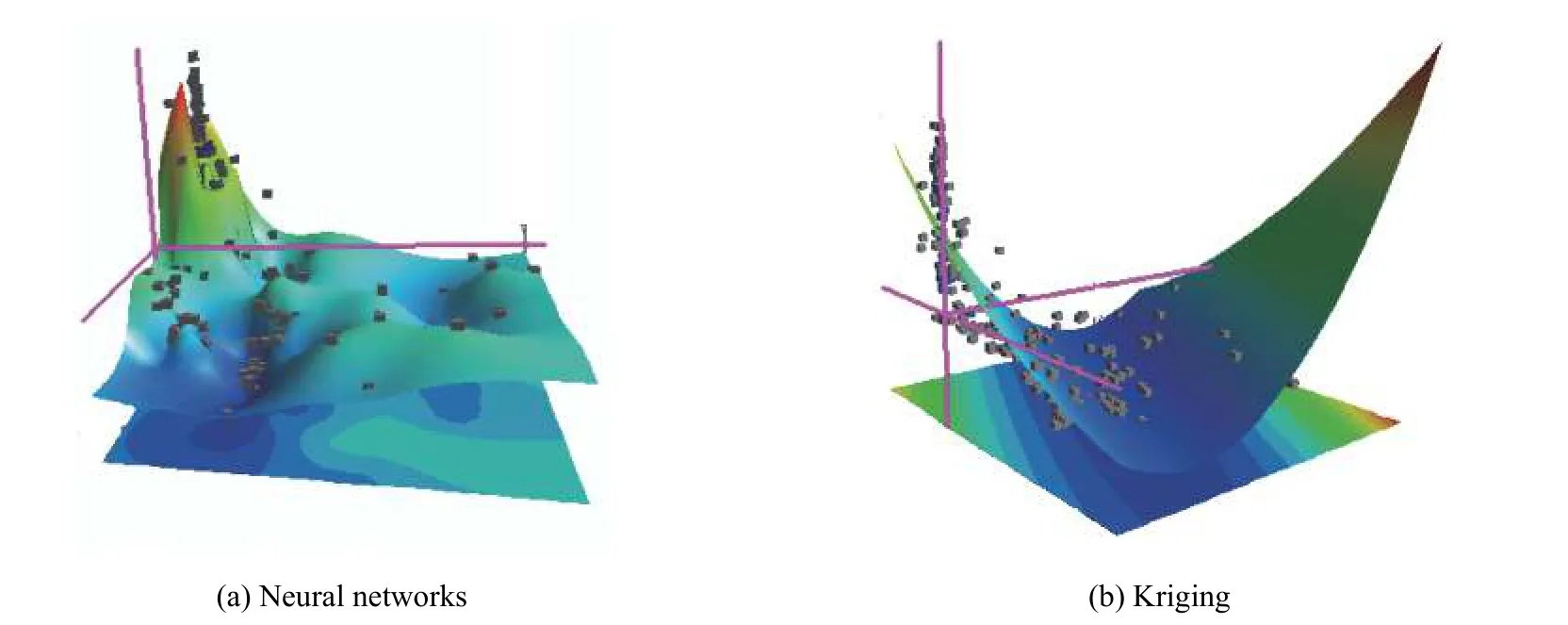
图7 神经网络模型与Kriging 模型对比Fig. 7 Comparison between neural network model and Kriging model
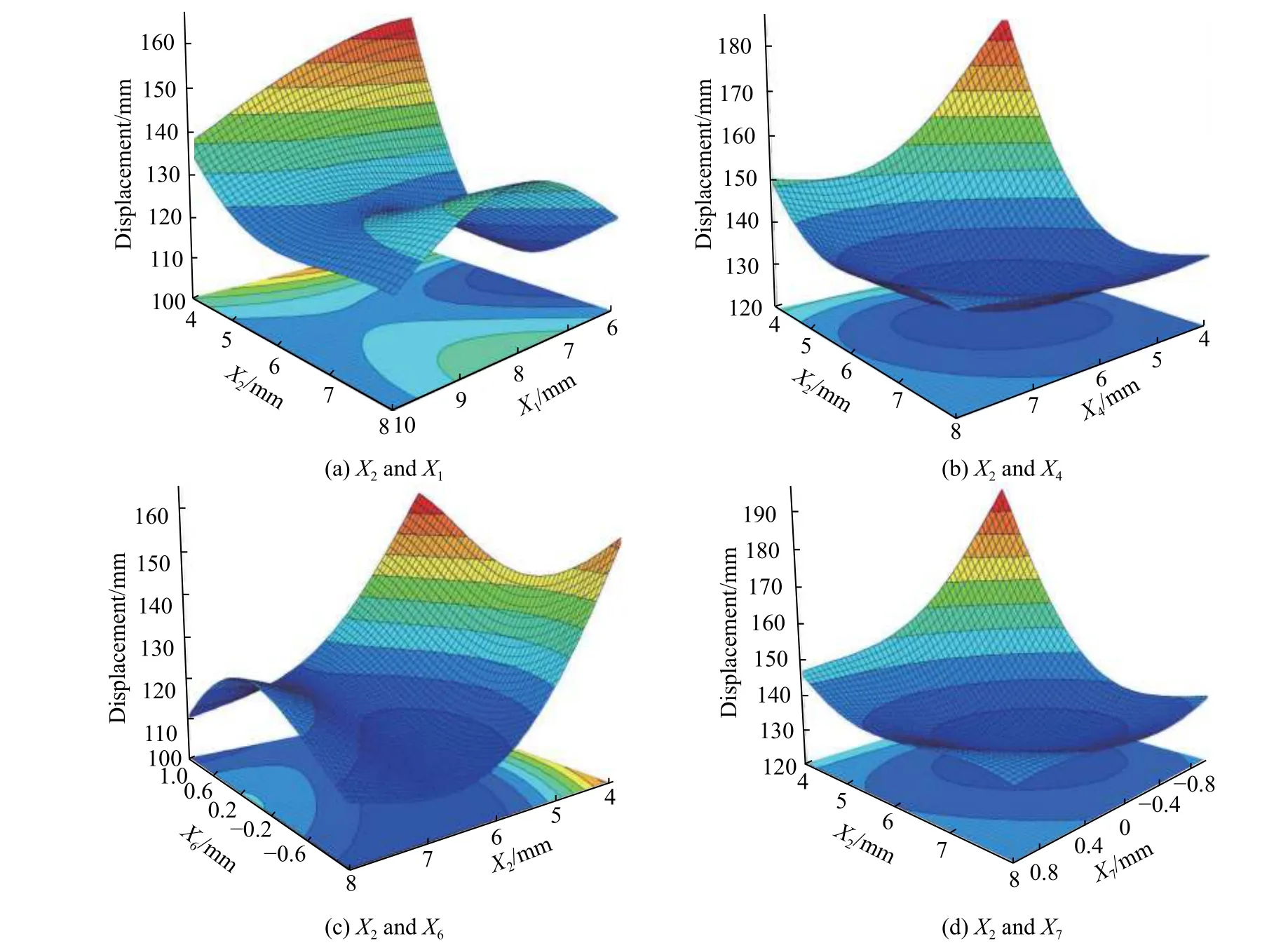
图8 主影响因子X2 分别与X1、X4、X6 和X7 拟合的位移响应面Fig. 8 Response surfaces of displacements where the main influence factor X2 fits X1, X4, X6 and X7, respectively
3 优化结果分析
3.1 抗冲击组件的帕累托前沿
利用帕累托原理的寻优算法对已构建的近似模型进行求解,获得由样本空间内最佳值构成的帕累托前沿。针对防护组件优化设计问题,主要运用径向基函数(RBF)神经网络与多目标遗传算法(MOGA)进行数值优化,基于帕累托的多目标遗传算法(MOGA)的核心在于非支配集算法的构成[18]。算法收敛的本质为非支配集不断接近于实际问题理论的帕累托最优边界的过程[19]。对防护组件结构的数学模型进行求解,改变数学模型为二维多目标优化问题,通过帕累托解集进行描述。遗传代数设为200 代,各精英数量占10%,变异率取值0.05,获得8 000 组解及对应的68 组帕累托解集如图9 所示,结合工程实际需要对优化结果的尺寸进行修正:X1=6 mm,X2=7.5 mm,X3=6 mm,X4=4.5 mm,X5=5 mm,X6=0.9,X7=-0.5。该优化结果(最优解)是由神经网络代理模型预测所得,为了验证优化结果的准确性,需对数值优化结果进行仿真计算与实验验证。
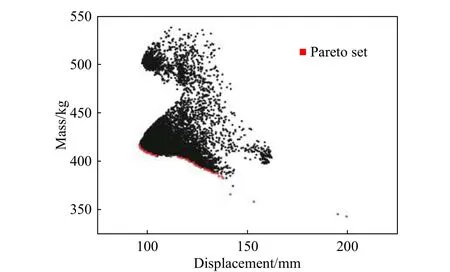
图9 帕累托最优解集Fig. 9 Pareto optimal solution set
3.2 优化结果实验验证
以同样的边界条件对优化设计出的防护组件进行实爆实验,从实验结果来看,优化后的防护组件可以在6 kg 当量的TNT 爆炸冲击下保持完整而不破裂。如图10~12 所示,较初步设计方案其防护性能提升显著,同时通过仿真分析得到防护组件背板实验损伤图。优化后防护组件背板变形量显著降低。由于背板最低点到背板安装点的垂向距离为100 mm,所以仿真模拟地板的最大变形量为139 mm,代理模型的数值为134 mm,其相对误差为3.6%,代理模型相对误差较小。从表4 可知,优化后模拟地板变形量减小36.2%,防护组件质量增加8.2%。背板塑性变形量为171 mm,实验后测得背板最大塑性变形量为176 mm,仿真结果与实验结果相对误差为2.8%。通过仿真与实验进一步验证该优化方案可靠,符合设计要求。

图10 抗爆组件优化后实验状态Fig. 10 Experimental status of anti-explosion components after optimization

图11 仿真与实验背板塑性变形图Fig. 11 Simulation and experimental plastic deformation of the back plate
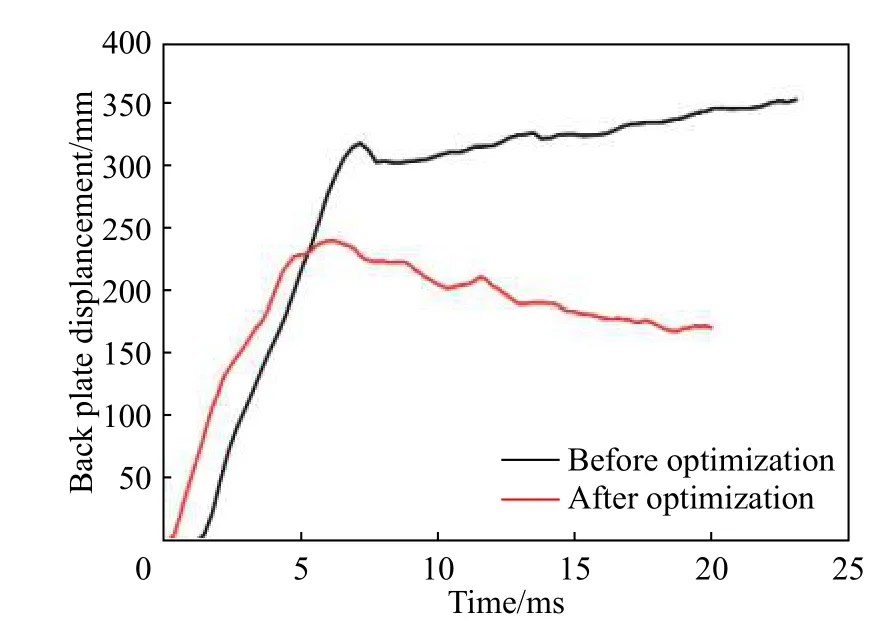
图12 背板位移曲线Fig. 12 Backplane displacement curves

表4 优化前后对比Table 4 Comparison before and after optimization
4 结 论
基于径向基函数神经网络代理模型结合多目标遗传算法对防护组件进行了优化设计,通过仿真分析、参数筛选,建立了该结构优化设计的准确的代理模型,在神经网络模型的基础上通过多目标遗传算法得到了帕累托最优解集,根据工程需求确定了防护组件的设计参数,并对其进行了仿真验证与实验验证,得到以下结论:
(1)通过参数灵敏度分析可知,背板厚度和面板与背板之间的横梁布置对防护组件防护性能的影响较大;
(2)通过神经网络代理模型结合多目标遗传算法对防护组件结构进行数值优化,提出了防护组件的最优设计方案,可以显著提升防雷板的防护能力;
(3)对于高度非线性工程问题,神经网络模型具有较高的拟合精度,对于工程优化设计问题具有很好的应用价值。
