有向无环图上k步可达查询优化算法
2020-04-09杨安平周军锋陈子阳
杜 明,杨安平,周军锋*,陈子阳,杨 云
(1.东华大学计算机科学与技术学院,上海201620;2.上海立信会计金融学院信息管理学院,上海201620)
0 引言
给定有向无环图(Directed Acyclic Graph,DAG)G,可达性查询u?→v用于回答从顶点u出发是否存在一条路径可以到达顶点v。实际应用中,如社交网络、通信与传感器网络、生物网络、可扩展标记语言(eXtensible Markup Language,XML)数据、资源描述框架(Resource Description Framework,RDF)数据等,可达性查询可用于检测两点间是否存在特定关系。可达性查询处理是图数据管理与分析的基本操作之一,是研究者广泛关注的热点问题[1-2]。然而,实际中除了检测两点间是否存在特定关系,还需要考虑关系的强弱程度,如存在信号衰减的传感器网络,用户更感兴趣的是长度受限的可达性查询。传统的可达性查询只能回答两个顶点间是否可达,并不能确定在几步内可达。本文研究k 步可达查询的高效处理问题。与基本的可达性查询相比,k步可达查询用于回答从u出发,是否存在长度在k 步之内的路径到v。传统的可达查询可以看作k=∞时的k 步可达查询[3]。由于k 步可达性查询体现着图中顶点对其他顶点的影响力,因而相对可达性查询而言,能提供更多的信息。
现有解决k 步可达性查询的方法主要分为两类:Label-Only[4]和Label+G[5-7]。Label-Only类方法的主要思想是通过构建所有可达顶点间最短路径的索引,当判断从顶点u能否在k步内到达顶点v 时,只需通过标签得到u 和v 之间的最短路径长度,然后比较从u 到v 的最短路径长度与k 的大小关系。当最短距离大于k 时,说明该查询不满足k 步可达性,否则说明该查询满足k 步可达性。Label+G 类方法的主要思想是快速构建部分可达信息的索引,处理查询时,若索引可回答查询,则直接返回结果;否则需要通过图遍历来得到最终结果。相比较而言,Label-Only类方法的索引规模大、索引构建时间长,且当查询不可达时,处理效率低。而现有的Label+G 类方法由于索引记录的可达信息少,查询处理时需要遍历的顶点较多,当满足条件的查询数量增多时,算法性能显著下降。
针对以上问题,本文提出一种求解k 步可达查询的高效Label+G算法kRH。其基本思想是通过快速构建索引规模小、可达信息覆盖广的索引,从而可以在常量时间回答更多的查询,同时降低图遍历的代价。具体来说,本文的工作如下:
1)提出一种基于部分点的双向最短路径索引,用于在常量时间回答大部分k 步可达查询,并提出三种启发式规则来减小索引规模。
2)提出基于简化图的正反互逆拓扑来提高不可达查询的处理效率。
3)提出远距离优先的双向搜索策略,并在此基础上提出高效的查询处理策略。
4)基于多个真实的数据集进行测试,实验结果显示,本文提出的方法比现有方法更高效。
1 背景知识及相关工作
1.1 数据模型及相关概念
本文处理有向无环图(DAG)上的k 步可达查询。给定DAG,V 表示顶点的集合,E 表示边的集合。后续讨论中,用(u,v)∈E 表示从u 到v 的边,δ(u,v)表示u 与v 的最短路径,Out(u)表示u 指向的顶点集,In(u)表示指向u 的顶点集。Out*(u)表示u 可达的顶点集,In*(u)表示可达u 的顶点集。给定G 中任意两个顶点u 和v,若从u 到v 存在一条有向路径,则说明u 可达v,否则说明u 不可达v。若从u 到v 存在一条长度不大于k 的路径,说明从u 出发k 步可达v,用u →kv 表示;否则u不能在k步可达v,用u↛kv表示。
对于一个DAG 来说,它体现顶点之间的偏序关系,通过拓扑排序,将顶点的偏序关系转变为全序关系,拓扑号即为全序关系的序号。顶点u、v 的拓扑号分别为Xu和Xv,若存在Xu>Xv,u不可达v。
1.2 相关工作
1.2.1 可达查询
针对图论中的可达性查询,按照索引覆盖范围的大小,分为两大类:1)构建全索引的方式;2)构建部分索引的方式。全索引方式的主要思想是通过记录任意两个顶点之间的可达信息来处理可达查询。基于该思想,文献[8]采用传递闭包的方式记录任意两个顶点间的可达信息,该算法虽然能够在O(1)的时间复杂度内处理查询,缺点是空间复杂度是,实际中扩展性太差,无法应用于大图。文献[9]采用压缩传递闭包的方式,通过向上向下遍历给图中每个顶点v 附加两个区间LIN(v)和LOUT(v)。当需要判断u 与v是否可达时,仅需要判断u 和v 之间是否存在交集,若交集不为空,则说明u 可达v;否则,u 不可达v。部分索引方式的主要思想是通过记录部分顶点之间的可达信息配合遍历的方式来处理可达查询。基于该思想,GRIPP算法[10]给所有顶点附加一个区间,并通过区间包含来判断顶点间是否可达,若区间不包含,则需要通过遍历的方法才能判定。Grial 算法[11]在GRIPP 算法的基础上,采用不同的遍历方式给图中所有顶点附加多个区间,同样是采用区间包含判定是否可达,对于不能判断的查询,需要采用遍历的方式才能够判断。FELINE 算法[12]通过给图中每个顶点附加两个整数,代表顶点在图中拓扑排序的序号,若顶点u 的拓扑序号大于v的拓扑序号,则可以判定u不可达v。
1.2.2 Label-Only方法
Label-Only 方法的思想是通过记录所有顶点对之间的最短路径长度来回答k 步可达查询。基于该思想,一种简单的方法是直接记录所有顶点对之间的最短路径长度,该方法虽然可以O(1)时间回答k步可达查询,但空间复杂度为在实际应用中可扩展性太差,无法处理大图。针对该问题,文献[9]提出一种压缩的最短路径索引PLL(Pruned Landmark Labeling)。其基本思想是为图中的每一个顶点v 建立LIN(v)和LOUT(v)两个标签,其中LIN(v)标签用来记录顶点v与In*(v)中部分顶点间的最短路径,LOUT(v)用来记录v 与Out*(v)中部分顶点间的最短路径。则u 和v 之间的最短路径δ(u,v)的计算问题就转换为求解中间节点和u、v 最短路径之和的最小值问题。当需要回答从u 到v 是否k 步可达时,只需判断LIN(v)和LOUT(v)是否存在交集。若不存在交集,则说明两个顶点不满足k 步可达;若存在交集,说明u 通过交集中的任意一个顶点都可到达v。基于交集结果,可得到所有交集顶点与u 和v之间的最短路径之和,则u和v之间的最短路径δ(u,v)就等于最短路径之和中的最小值。如果δ(u,v)≤k,说明u →kv;否则,说明u↛kv。
该方法的问题在于两方面:1)索引规模大、索引时间长,原因在于需要记录完整的最短路径信息;2)对不可达查询的处理效率较低,原因是LOUT(u)与LIN(v)的交集为空意味着需要访问LOUT(u)与LIN(v)中的所有信息。
1.2.3 Label+G方法
由于通过直接遍历回答查询的效率太低,而Label-Only方法的索引时间长、索引规模大,研究者试图通过仅记录部分k 步可达信息来在效率方面进行平衡。其基本思想是在线性或者近似线性时间复杂度内记录部分k 步可达信息,用于减小遍历操作的搜索空间,根据其剪枝能力的不同,分为三种类型的方法。
第一类方法是直接使用传统的可达查询处理方法[10-11]来回答不可达查询,对于可达查询,通过直接遍历的方法检测是否满足k 步的条件。该类方法虽然索引时间少,索引规模小,但当满足条件的查询数量增多时,效率异常低下。
第二类方法是构建可回答部分k 步可达查询的索引来加快查询处理的速度。文献[5-7]基于顶点覆盖技术构建k 步索引。其基本思想是首先求得原图的一个顶点覆盖集合,然后在顶点覆盖集上构建传递闭包作为索引,最后根据该索引来处理k 步可达查询。这种方法的问题是索引只能回答固定k值的可达查询,扩展性较差。
第三类方法[3]采用FELINE 算法[12]作为特定的剪枝条件,来快速回答不可达查询,对于其他查询,则提出基于广度优先生成树以及广度层作为剪枝条件来提高k 步可达查询的处理效率。该方法为生成树的每个顶点附加一个区间,用于判断顶点之间的祖先后代关系。若L(v)⊂L(u),说明v 是u 的后代,则查询可通过比较u 和v 之间的层数差来判断;若L(v)⊄L(u),说明v不是u的后代,则需要递归判断u的后代中是否存在顶点p,满足L(v)⊂L(p)。该算法的缺点是生成树的区间覆盖率很低,因此,当满足条件的查询数量增多时,查询效率较低。
相比较而言,Label-Only方法虽然查询处理时无需遍历操作,但索引规模大、索引构建时间长,同时对不可达查询的处理效率较低;而Label+G 方法虽然索引构建时间短、索引规模小,但查询处理时因需要遍历操作而显得效率较低,尤其是当满足条件的查询增多时,效率显著下降。本文针对该问题,提出一种增强的Label+G 方法,在降低索引规模的前提下,通过增强不可达查询和可达查询的剪枝效果来缩减遍历操作的搜索空间,提升k步可达查询的处理效率。
2 基于部分点的双向最短路径索引
2.1 双向最短距离索引的基本思想
本文提出基于部分出度与入度之和较大的顶点(简称hop点)建立双向最短路径索引来加速k 步可达的判断,这里双向的意思是不仅记录a与其可达点的最短距离,而且记录a与可达a 的点的最短距离。具体来说,类似于2hop 索引[4],本文为每个点v 设定两个标签LIN(v)和LOUT(v)。和2hop 索引的不同在于,两个标签中不仅仅记录了可达信息,而且记录了最短路径信息。其中前者LIN(v)用于存储可达v 及其与v 的最短路径,后者LOUT(v)存储v可达的点及其与v的最短距离。
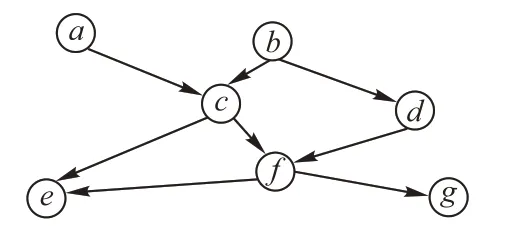
图1 有向无环图G的示例Fig.1 Example of DAG G
例如,对图1 的G,假设顶点的处理顺序是c →a →b →d →e →f →g。当 处 理c 时,其 可 达 点 为c,e,f,g,可达c 的点为a,b。因此将元组加入到LIN(u()其中u ∈{c,e,f,g})中,这里dis 表示c 到u 的最短路径长度。类似地,将加入LOUT(v)中(其中v ∈{a,b}),这里dis表示v和c 的最短路径长度。表1 是基于图1 所有顶点构建的最短路径索引。

表1 基于所有顶点的最短路径索引Tab.1 Shortest path index based on all points
基于表1的索引,则给定任意两点a和b,判断a是否可在k 步到达b,则只需比较LOUT(a)和LIN(b):如果二者的交集为空,说明a 不可达b;否则说明a 可达b。如果a 可达b,将a 通过交集中每个点到达b 的路径长度计算出来,取其最小值即为a 和b 的最短路径长度。如果该长度小于给定的k 值,则说明a可以在k步可达b,否则a不能在k步到达b。
2.2 双向最短距离索引的优化
虽然该索引可回答所有查询,且无需在图上执行遍历操作,但其索引规模太大,且求解交集的代价太高。为此,提出仅构建部分点的双向路径索引来减小索引规模。原因在于:1)实际中的图存在少量度很大的点,相应地,其可达顶点也通常比较多,选择这样的点构建双向最短路径可以显著增加所维护的可达点对数量及通过这种点的最短路径长度。2)我们的实验表明,对一般图来说,要么32 个点已经维护了足够多的可达信息,再增加顶点后,可达信息并没有明显增加;要么32 个点仅维护少量可达信息,再增加这种点同样不会显著增加可达信息维护量。如图2 所示,从实际数据上的测试结果可以看出:对于amaze 数据集,即使k=1,双向索引的可达覆盖率也可接近100%;而对cit-Patents 而言,即使k 值增加到32,可达覆盖率依然非常小;另外两个数据集上,当k 值增加到16以后,数据基本不再发生变化。
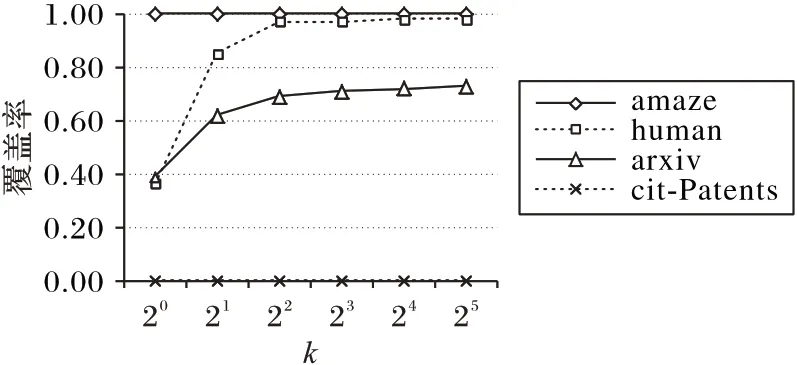
图2 k个hop 点可达覆盖率Fig.2 Coverage of reachability for k hop nodes
基于以上观察,取32 个点构建双向最短路径索引。假设对于图1 所示的DAG G,本文取c 和f 两个点构建双向最短路径索引,如表2 所示。显然,和表1 的索引相比,表2 的规模降低了。实际上,表2还可以进一步优化。

表2 基于c和f的最短路径索引Tab.2 Shortest path index based on c and f
定理1当基于顶点v 构建双向最短路径索引时,如果向上(向下)遍历的过程中遇到了已处理的hop 点u,则无需从u继续向上(向下)遍历。
证明 如图3 所示,假设x 可达u,当前处理的是hop 点v,hop点u在v之前处理。当从v向上遍历时遇到了u。基于u得到的标签,假设求得x 到u 的距离是d1,u 到v的距离是d2,则x通过u 到v 的距离是d1+d2。显然,从v 向上遍历遇到u,所求u 与v 之间的距离仍然是d2,因此即使在u 不停止,所得x 和v的距离仍然是d1+d2,因此,无需从u继续向上遍历。
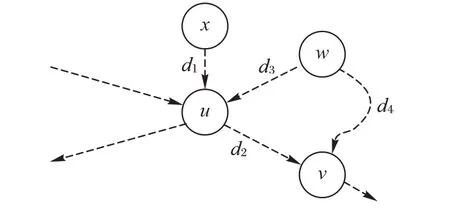
图3 hop点作用示意图Fig.3 Schematic diagram of hop nodes intension
定理2当基于顶点v 构建双向最短路径索引时,如果向上(向下)遍历的过程中通过非hop点遇到了w,且w通过u到v的距离小于w 通过非hop 点到v 的距离,则无需从w 继续向上(向下)遍历。
证明 如图3 所示,假设hop 点u 先处理,目前处理的是hop 点v。假设从v 向上遍历,通过非hop 点到达w,路径长度是d4。如果w 和u的最短距离是d3,且d3+d2≤d4,显然无需在LOUT(w)中记录其和v 的距离d4,因为d4不是最短距离。因此,无需从w开始继续向上遍历。
基于定理1和定理2,在求解双向最短路径索引的过程中可有效减小索引规模,提高索引构建的速度。例如,对图1 的G 而言,假设选择两个hop 点c 和f 来构建双向最短路径索引。先处理的是点c,当处理第二个点f时,当从其向上遍历遇到第一个hop 点c时,可根据定理1 立即停止遍历,当从非hop 点遍历到b 时,可根据定理2 立即停止遍历。当处理完这两个点后,所得到的双向路径索引如表3所示。
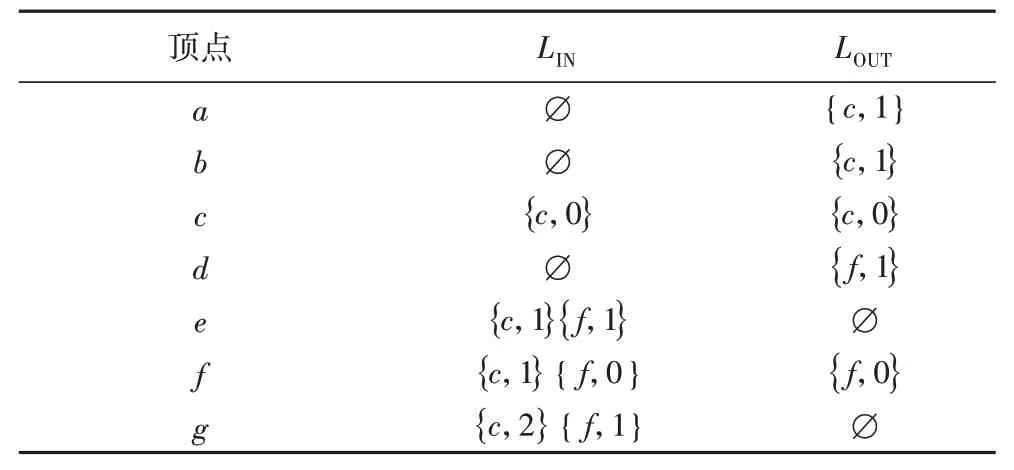
表3 基于c和f的优化后的最短路径索引Tab.3 Optimized shortest path index based on c and f
3 基于栈的正反互逆拓扑
可达是k步可达的必要条件,因此,若查询不可达,则必定k步不可达。基于此,本文使用拓扑序号为基础的方法来快速判断不可达。其基本思想是:给定两个顶点u和v,若u的拓扑号大于v的拓扑号,则u不可达v,因此u在k步内不可达v。
文献[3]通过使用互逆的两个拓扑号来增强不可达查询的判断能力。具体而言,给定第一个拓扑顺序,在构建逆序拓扑时,始终优先访问第一个拓扑号最大且所有入邻居均被访问的顶点。以此建立的拓扑称为第一遍拓扑的逆向拓扑。虽然实际中互逆拓扑可快速判断很多不可达查询,但仍然存在两方面的问题。
首先,在实际应用中,基于正向建立的两个互逆拓扑号仍然存在很多不可达查询无法判断的问题。针对该问题,本文提出构建正反互逆拓扑来过滤更多的不可达查询。其基本思想是:首先,删除已处理的hop 点。原因是与hop 点关联的最短路径均已处理完毕,后续的最短路径计算与其无关。删除hop点之后,数据图得以很大程度上的简化。其次,自顶向下、以深度优先的方式构建正向互逆拓扑。最后,沿着边的相反方向,以自底向上,以深度优先的方式构建反向互逆拓扑。
其次,文献[12]基于堆求解逆序拓扑,其时间复杂度为O(|V|log|V|)。本文设计了高效算法在线性时间构建正反互逆拓扑。与以上工作相比,由于首先删除了hop 点,因而所建立的正反互逆拓扑可以过滤更多的不可达查询。和文献[12]相比,本文提出的正反互逆拓扑索引具有线性的时间复杂度,同时能过滤更多的不可达查询。和文献[3]的方法相比,由于我们在求解正反互逆拓扑之前去除了hop 点,数据图得以很大程度的简化,因而效率更高。
4 索引构建
4.1 基于hop点的最短距离索引构建
4.1.1 算法描述
给定DAG G,求解hop 点的最短路径索引总体上分为3步。首先求解hop 点,然后基于hop 点执行广度优先遍历(Breadth First Search,BFS)建立LIN索引,最后基于hop 点执行反向BFS建立LOUT索引。下面分别予以说明。
(1)根据(In(v)+1)*(Out(v)+1)从大到小的顺序选择前32个顶点作为hop点。如算法1第1)行。
(2)从hop 点v 开始执行BFS,对于遍历到的顶点u,若是通过标签计算得到了长度大于从v 到u 的路径长度,则更新LIN(u)并继续访问u可达的点;若是通过标签计算得到的长度小于从v 点到u 的路径长度,则不更新LIN(u)且不再从u 出发继续BFS。如算法1第2)~12)行所示。
(3)从hop点开始执行反向BFS,对于遍历到的顶点u,若是通过标签得到的长度大于从hop点到u的路径长度,则更新LOUT(u)并且访问u的父亲;若通过标签得到的长度小于从hop点到u 的路径长度,则不更新LOUT(u)且不访问u 的父亲。如算法1第13)行所示。
算法1 hop(G=(V,E))。

算法1 用于求解基于hop 顶点的最短路径,其中QU(v,u,LOUT(v),LIN(u))表示通过标签求解得到从v 到u 的最短路径长度,Dis(v,u)表示基于BFS得到从v到u路径长度,初始值为0,Q表示队列。算法1中第1)行按照规则选择度大的32 个顶点作为hop 点。第2)、3)行将hop 点依次执行入队操作。当队列不空时,执行出队操作(第5)、6)行)。若通过标签求得的最短路径不大于遍历的路径长度,则停止访问其后代(第7)、8)行);否则,更新LIN标签,并将其后代加入到Q 中(第9)~12)行)。将hop点v再入队列,通过执行反向BFS构建第13)行)。
注 意,算 法1 中 需 要 在 第7)行 调 用 函 数QU(v,u,LOUT(v),LIN(u))求解根据已处理hop 点得到的路径长度。这一操作需要比较LOUT和LIN,即执行集合求交集的操作。为了加快集合交集操作的处理,需要先对集合中的顶点按照编号,或者某种序号进行排序。
4.1.2 索引优化
若v 和u 之 间 通 过hop 点 有 路 径 相 连,则 函 数QU(v,u,LOUT(v),LIN(u))进行集合交集操作的结果是经过hop 点相连的路径长度,无需知道hop 点是谁。因此,采用如下规则对算法1进行优化。
规则1 所有顶点的LIN或者LOUT中无需存储顶点自身编号,只需存储代表顶点处理顺序的数字即可。
根据规则1,构建索引时,无需执行排序操作,对第i 个处理的hop 点,直接在相应顶点的标签中加入即可,这里的i表示当前hop点是第i个被处理的hop点,dis是hop点和当前点的最短路径距离。
进一步,由于只选择了32个hop点,且实际中数据图的拓扑层数有限,因此无需使用两个整数来表示标签中的元组。利用规则2来进一步减少索引规模。
4.2 正反互逆拓扑构建
求解正反互逆的拓扑号索引总体上分为4 步:首先删除32 个hop 点,然后求解正向的拓扑号X,接着基于X 求其逆向拓扑号Y,最后在反向图上求解两个拓扑号索引M和N。
给定一个有向无环图G,可以通过以下步骤得到X:1)将G中入度为0的顶点入栈S。2)对栈中元素执行以下操作:(a)将S的栈顶元素v出栈,并标记v的拓扑顺序;(b)删除v及所有从v 出发的边;(c)将v 的孩子中入度为0 的顶点插入S。3)重复步骤2)直到S为空,相应的顶点出栈顺序称为X。
给定X,同样基于栈可以得到其逆向拓扑顺序Y。基本操作方法如下:首先所有入度为0 的顶点按照它们在X 中从小到大的顺序进入栈S。对栈中元素执行以下操作:1)将S的栈顶元素v 出栈,并标记v 的逆向拓扑号;2)删除v 及从v 出发的边;3)将v的孩子中入度为0 的顶点按照它们在X 中从小到大的顺序入栈。执行上述步骤,直至栈空即可得到第二次拓扑顺序Y。
定理3求解逆向拓扑时,栈顶元素和使用堆选择的拓扑号最大的元素为相同顶点。
证明 首先,使用大顶堆时,堆顶元素是当前堆中拓扑号最大的顶点。其次,使用栈时,本文首先将入度为0 的顶点按照第一遍拓扑的顺序从小到大入栈,因此可以保证对初始入度为0 的顶点,栈顶元素的拓扑号最大。最后,由于栈顶元素的拓扑号最大,其孩子的拓扑号必然也大于栈中元素的拓扑号。每处理一个栈顶元素,其孩子中可进一步拓扑的顶点也是按照第一遍拓扑的顺序从小到大入栈,这样可以保证栈顶元素始终具有最大的拓扑号。因而可以保证每次处理的都是可拓扑的顶点中拓扑号最大的。
算法2 genTopo(G=(V,E))。
输入 G=(V,E);
输出 所有顶点v的四个拓扑序号X,Y,M,N。
1) 从G中删除32个hop点
2) Construct(G,X)
3) Construct(G,Y)
4) 将G的边反转,执行第1)~2)行,求解反向互逆拓扑
第2)、3)行都是调用的Construct函数,代码如下所示:
Function Construct(G=(V,E),H)
1) 将入度为0的顶点按照特定顺序入栈S
2) topoNum ←0
3) while S ≠∅ do
4) v ←pop(S)
5) HV←topoNum
6) topoNum ←topoNum+1
7) for each u ∈Out(v) do
8) insize(u)←insize(u)-1
9) if insize(u)=0 then push u into S
在得到正向互逆的拓扑后,将图的边反转,在反向图上执行上述步骤,从而得到反向图上的拓扑号M 和N。最终,这4个拓扑顺序构成本文提出的正反互逆的拓扑号索引。
算法2 用于求解给定的DAG G 的正反互逆拓扑序号,其中第2)行调用函数Construct 求解第一个拓扑顺序X,第3)行求X 的逆向拓扑Y,第4)行求解反向互逆拓扑M 和N。函数Construct 用于根据特定顺序得到一个拓扑序号,其中S 为栈,Hv表示顶点的拓扑序号。insize(v)表示存储顶点v 入度的临时数组。第1)行将图中入度为0 的顶点入栈。从第3)~9)行的迭代中,每循环一次处理一个顶点。具体做法是,第4)~5)行元素出栈并设定其拓扑号,然后在第7)~9)行将其出邻居的入度减1,若入度为0,则将其入栈。需要注意的是,算法第1)行,对于第一和第三遍拓扑,特定顺序不代表任何含义,只要找到一个入度为0 的顶点就将其入栈。第二遍和第四遍求的分别是第一、三遍的逆向拓扑,这时,特定顺序代表在第一边拓扑后,根据第一遍拓扑序号的升序将入度为0 的顶点入栈,这样就能保证第一、二遍拓扑互逆,第三、四遍拓扑互逆。另外,第7)行按照存储顺序处理,当执行第一遍拓扑后,图的邻接表中顶点按照拓扑号升序排序,且第二遍处理的是基于拓扑排序后的邻接表进行处理。这么做是为了在保证互逆的基础上,避免排序操作。
对图1的G 而言,在求解正反拓扑号之前,首先删除32个hop 点,得到简化的图,之后执行算法2 后,给每个顶点赋予4个拓扑号。
给定DAG G=(V,E),删除32个hop点的操作可在线性时间内完成。由于函数Construct 在执行过程中始终没有执行特定的排序操作,在每次执行函数Construct时,每个顶点v 的处理代价是,因此函数Construct 的时间复杂度是。算法2 总共调用了4 次函数Construct,因此算法2的时间复杂度是。
5 查询
算法3 用于判定查询的k 步可达性。其中QU(v,u,LOUT(v),LIN(u))表示通过标签求解得到的最短路径长度。算法3的第1)、2)行采用hop点的最短路径索引判定该查询是否满足k步可达性。具体来说:若通过最短路径索引求得从u到v的最短路径不大于k,说明该查询满足k步可达;否则若最短路径大于k并且查询中的顶点存在hop点,说明该查询不满足k 步可达性(第3)行)。若上述条件均不能判定查询的k 步可达性,则在第4)、5)行采用正反互逆的拓扑号判定查询的可达性:若查询不可达,则说明该查询不满足k 步可达;否则,在第6)~13)行以递归的方式执行遍历操作。
算法3 kRH (u,v,k,G=(V,E))。
输入 G=(V,E);
输出 true or false。
1) if QU(v,u,LOUT(v),LIN(u))≤k
2) return true
4) if Xu>Xvor Yu>Yvor Mu<Mvor Nu<Nv
5) return false
6) if Out(u) ≤ In(v) then
7) for each p in Out(u)do
8) if kRH(p,v,k-1)
9) return true
10)else
11) for each p in In(v) do
12) if kRH(u,p,k-1)
13) return true
基于如下两个启发式来加速遍历的过程。
规则3 给定k 步可达查询的两个端点u 和v。若u 的出度大于v 的入度,则从v 出发向上遍历找u;否则从u 出发向下遍历找v。
规则4 当从v 出发遍历时,优先选择与其拓扑层相差大的顶点w进行遍历。
规则4 中拓扑层相差较大,说明v 通过w 可能更快到达目标点。
6 实验与结果分析
6.1 实验环境
根据相关工作分析可知,在Label-Only 类算法中,PLL 查询效率最高;在Label+G 类算法中,根据文献[3],BFSI-B(Breadth First Search Index-Bilateral)算法比k-reach[5]更快,是Label+G类算法中查询效率最高的算法。因此,本文实验中用于比较的算法有BFSI-B[3]和PLL[9]。对于Label+G中第一类方法而言,例如GRAIL,因其并非专门处理k步可达查询,本文不再进行比较。所有算法都采用C++实现,并使用GCC7.3.0进行编译。所有算法使用相同的数据集和查询集,并在相同的平台上运行得到实验数据。机器配置是4 GB RAM 的Intel Core i5-3230 CPU(8 核,2.60 GHz)和Ubuntu18.04LTS。以索引规模、索引构建时间、查询时间作为评价指标来比较三种算法的性能。本文方法中的hop点个数是32。
6.2 实验数据集
实验数据集由21 个真实的数据集组成,这些数据集都广泛地出现在图论的可达性查询研究[14-16]中,它们的统计信息如表4 所示。其中arxiv、citeseer、pubmed 来自引文献[14];cit系列的数据集来自文献[6],其非叶子顶点的平均出度为10到30;uniprot100m、uniprot150m 来自Uniprot 数据库的注释联合 图[15],皆 是UniProt 的 完 整 资 源 描 述 框 架(Resource Description Framework,RDF)的子集;soc-LJ(soc-LiveJournall)是来自社会网络的有向无环图;wikiTalk是来自维基百科的有向无环图;web-Google 是来自Google 网页的有向无环图;dbpedia 为知识图;web-uk 是文献[16]收集的网络有向无环图。由表4 可知,除了前5 个数据集的规模较小之外,其余数据集规模较大;|V |表示给定有向无环图的顶点数量,|E |为边的数量,|d |表示顶点的平均度。对于每个数据集,本文使用随机生成的100 万个查询进行测试,算法的运行时间为处理100万个查询的总时间。
6.3 索引大小及时间
表5 和表6 分别给出了不同方法的索引大小和索引构建时间。从索引大小来看,如表5 所示,可以看出:1)在所有数据集上,本文方法构建的索引规模最小。2)对于规模较小的图而言,三种方法的索引规模相差不大。3)当图是稠密图时,PLL 算法建立的索引规模最大。原因在于,PLL 要构建所有点的双向索引,而BFSI-B 的索引规模与图的顶点个数成正比,每个顶点对应8个整数。本文方法kRH为每个顶点设定4个拓扑号。虽然建立的是32 个hop 点的索引,但由于使用了提前终止条件以及每个hop 点关联的顶点有限,平均到每个点,hop标签不会超过4个数字,因此索引规模比BFSI-B小。
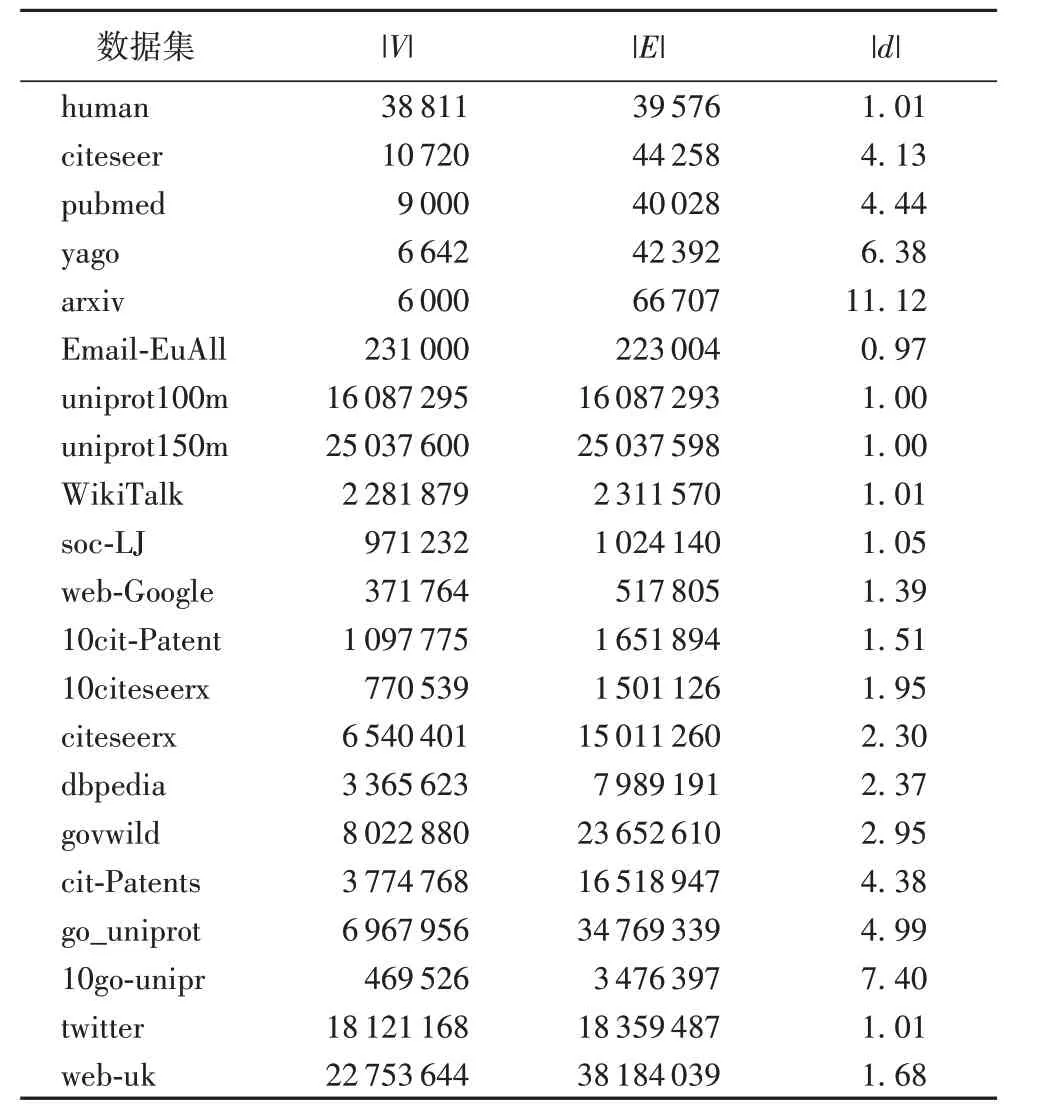
表4 实验数据集统计信息Tab.4 Statistics of experimental datasets
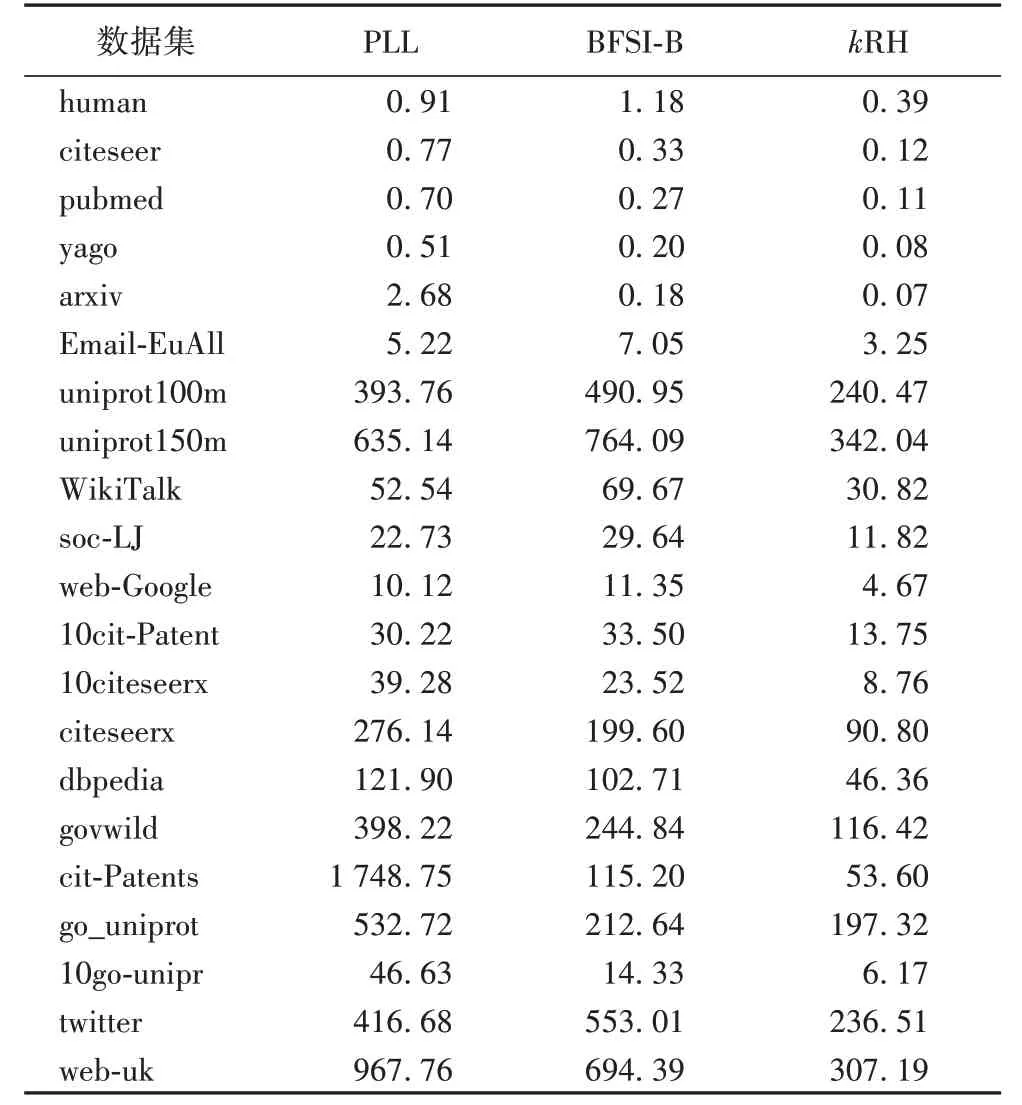
表5 不同数据集上的索引大小 单位:MBTab.5 Index size on different datasets unit:MB
在索引时间方面,如表6 所示。相比PLL,kRH 算法的索引构建时间更短,尤其当图的规模大且稠密时更加明显;相比BFSI-B,二者索引时间相差不大。
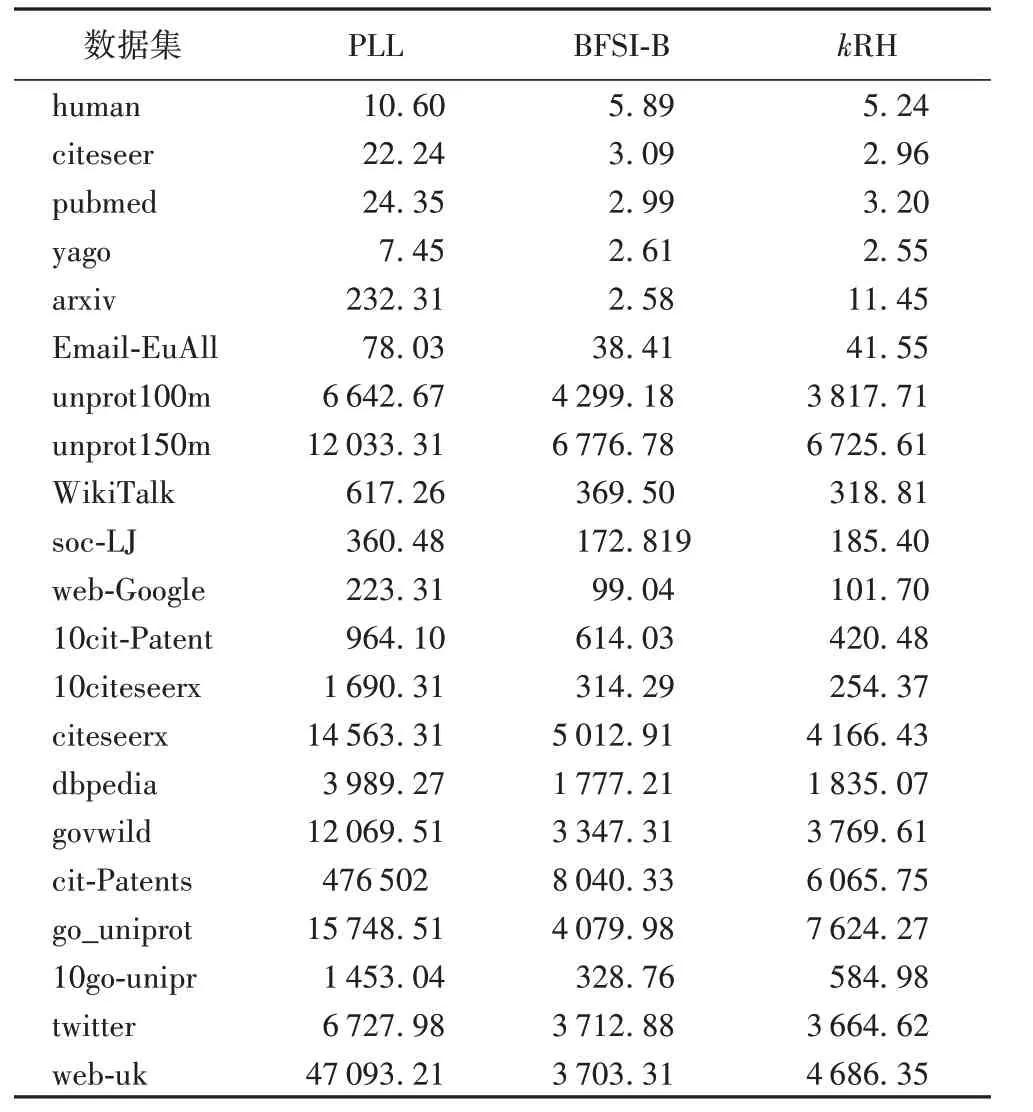
表6 不同数据集上的索引时间 单位:msTab.6 Index time on different datasets unit:ms
6.4 查询时间
表7 展示了三种算法当k=3 时的查询处理时间。由表7可知,三种方法相比,本文算法所需时间最短。原因有两方面:一方面,和PLL 相比,本文算法可以在常量时间处理不可达查询;另一方面,和BFSI-B相比,本文算法基于4个拓扑号,可在常量时间检测更多的不可达查询。由于PLL不能常量时间回答查询,因此在表8 中和BFSI-B 比较了常量时间内可判定的查询个数,可以看出本文算法可在常量时间内判定更多的查询,因而可以获得比BFSI-B更高的查询响应速度。
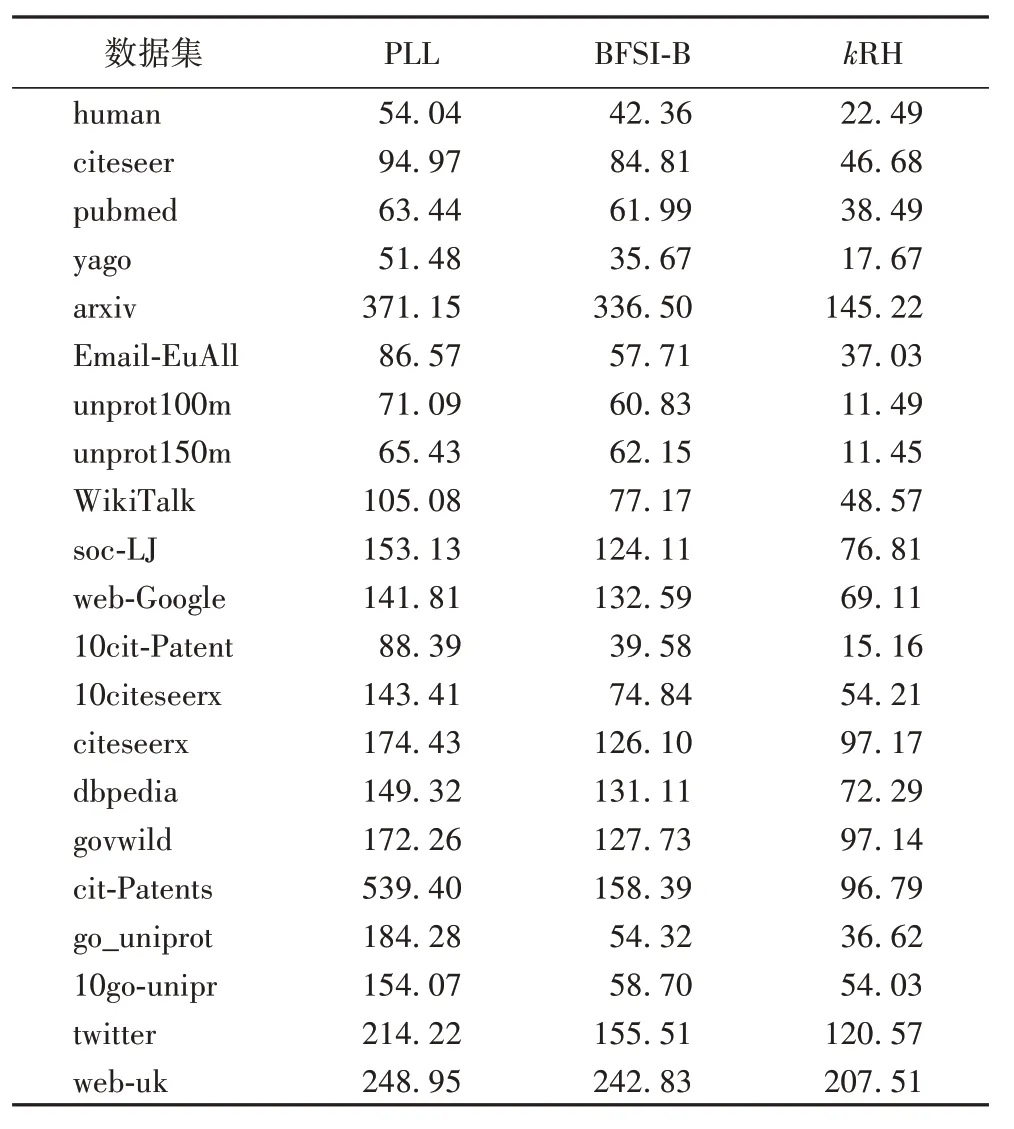
表7 k=3时不同数据集上的查询时间 单位:msTab.7 Query time on different datasets when k=3 unit:ms
6.5 不同k值的查询处理性能
图4 分别展示了三种算法在不同特征的数据集上处理100 万个查询时随k 值变化的情况。可以看出,本文方法和PLL 对k 值的变化不敏感,而BFSI-B 的性能受k 值影响较大,随着k 值的增加,其所需的查询处理时间增长较多。对于稀疏数据集来说,k 值的变化对于BFSI-B 和kRH 算法的查询时间影响不大;而对于稠密数据集(go_uniprot)来说,BFSI-B 和kRH 算法的查询时间随着k 的增大而增加,但是BFSI-B 的增加幅度更大。这是因为kRH算法比BFSI-B覆盖程度更高。
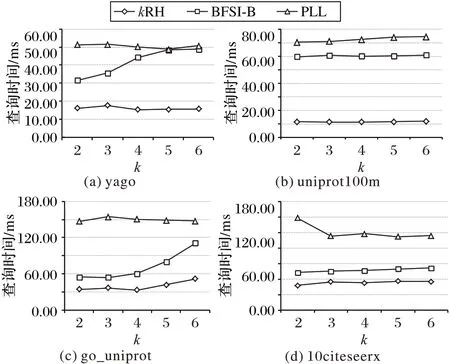
图4 不同数据集上三种算法的查询时间对比Fig.4 Query time comparison of three algorithms on different datasets
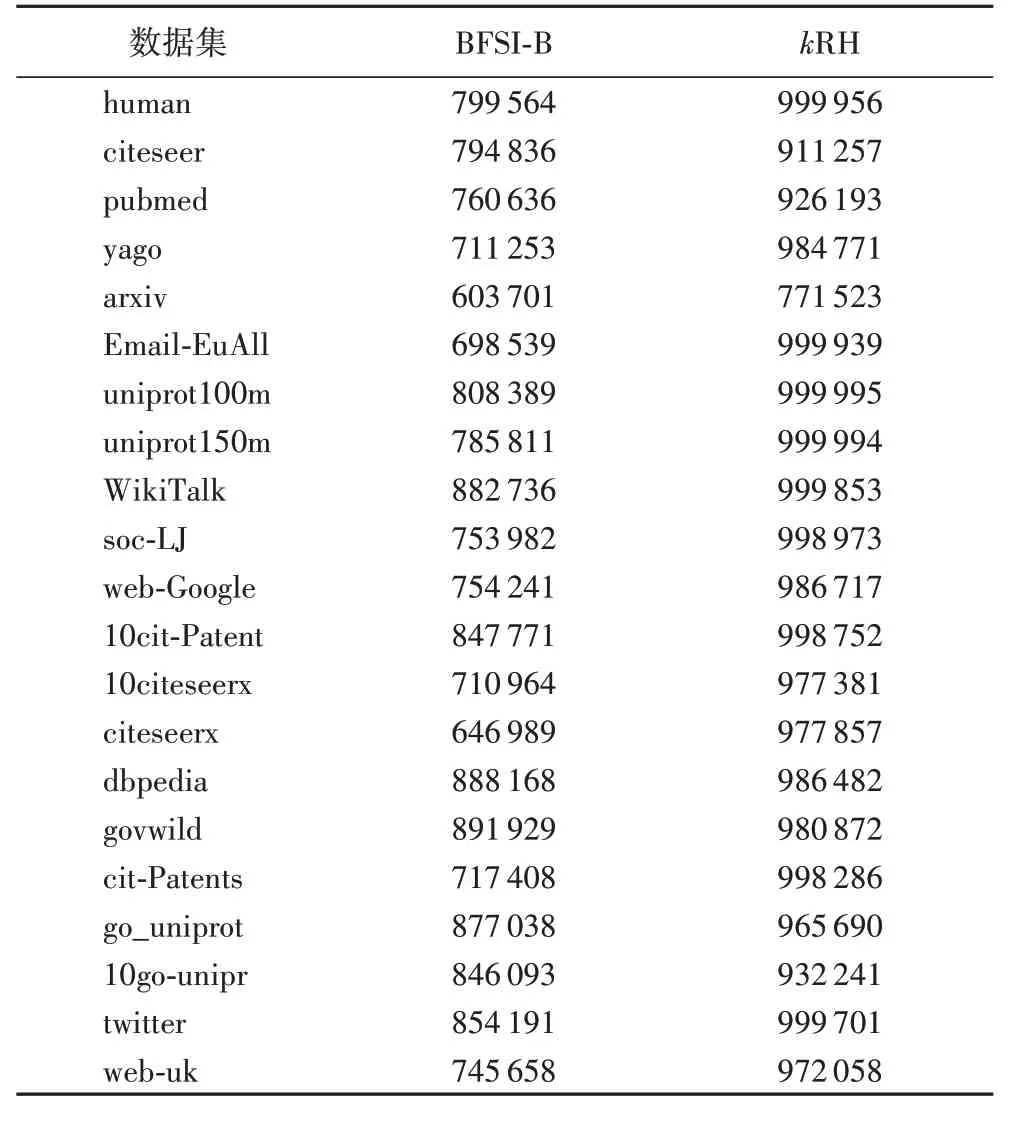
表8 k=3时常量时间内可判定的查询数量Tab.8 Query answers can be determined in constant time when k=3
7 结语
针对已有k 步可达查询方法存在的索引规模大、查询响应速度慢的问题,本文提出通过构建大度顶点的双向最短路径来提高可达查询的覆盖率,同时提出基于简化图的正反互逆拓扑来提高常量时间内不可达查询的处理效率。本文还提出了一系列优化方法来减小索引规模、提高查询处理的效率。基于真实数据集的实验结果表明,本文算法具有较小的索引规模和更快的查询响应速度,同时具有较好的扩展性。最好情况下,在cit-Patents数据集上,与PLL算法相比,本文算法的索引规模和索引构建时间仅为PLL 算法3%,查询时间仅为PLL 算法的20%;和BFSI-B 算法相比,本文算法的索引仅为BFSI-B算法索引规模、查询时间的一半。
