Graphlet Degree Vector方法的优化与并行

宋祥帅，杨伏长，谢 江*，张 武，2

（1.上海大学计算机工程与科学学院，上海200444；2.上海大学上海市应用数学与力学研究所，上海200444）

0 引言

比较生物网络的相似和差异是当前计算生物学的一个主要问题［1］，生物网络通常由图来建立模型，图中节点表示生物分子，如代谢物、蛋白质、基因等，而边则表示各生物分子之间的相互作用［2］，研究生物网络可以为疾病的发生机制和治疗手段提供深刻的见解［3］。其中，一项很重要的研究就是寻找生物网络中的自同构轨道。Graphlet Degree Vector（GDV）方法是Przulj在2003年提出的利用图元及图元向量来刻画网络中节点邻域关系的方法，具体指在小连通非同构子图中计算每个节点的自同构轨道，即每个节点所接触的图形数量［4］，这种方法基于网络拓扑和邻域定义了一系列非同构子图和图向量，用于识别网络中结构相似的模块［5］。人们利用这种方法进行了许多有意义的研究［6］，例如研究了生物网络与随机网络的拓扑结构差异［7-8］，构建生物网络的进化树［9］，识别癌症相关基因［4］，计算差异网络的聚类系数［9］，生物网络进行最优比对［10］和蛋白质功能分析［11］等。然而随着小连通非同构子图中节点数的增加，GDV 方法的计算时间复杂度会很高，它的扩展会受到很大的约束［3］。尽管Przulj［8］提出可以利用提高CPU的性能来提高扩展性，但是计算成本会变得越来越高，因此随着生物网络研究的规模以及小连通非同构子图规模的不断增大，参与枚举的自同构轨道数量呈指数级别的增长，计算量越来越大，给图元的扩展带来了挑战。

当前图元方法仍以Przulj 于2003 年提出的GDV 方法为主流［12］，具体实现如Xie 等［5］于2017 年提出的基于2-4 nodes的枚举方法，通过一个二维矩阵Net_Matrix 来存储无向生物网络，然后通过枚举的方式找出2-4 nodes 连通非同构子图的15 个自同构轨道，该算法通过枚举的方式实现了轨道的查找，有效地完成了自同构轨道查找的任务。Hočevar 等［13］在2014 年提出了一种新的计算网络节点图形和轨道特征的组合方法，取得了比较显著的效果。此外，由于复杂度的原因，Ahmed 等［14］只研究了节点为3 和4 的图元，利用4 个节点和3个节点的图元在结构上相似性，减少判断包含4 个节点的图元向量的计算开销。

目前，已有的GDV 方法在计算规模上都存在瓶颈［15］。随着生物网络数据获取的渠道越来越多，生物网络规模越来越大，对计算效率的要求也会越来越高［15］，因此，实现高效的并行化GDV 方法很有必要。本文从文献［5］实现的串行的GDV方法着手，将该串行方法以消息传递接口（Message Passing Interface，MPI）为基础实现并行化，并结合去除原来算法的重复运算部分和负载均衡策略改进并行算法，最后，通过仿真数据和真实数据进行了分析和讨论。

1 GDV方法的主要思想

GDV 方法的主要思想是计算一个生物网络中每个节点的自同构轨道数量，即每个节点所接触的图形的数量［4］。这在研究生物网络的过程中发挥着重要的作用。

图1 展示了包含2、3、4 个节点的非同构图元。为了刻画节点的拓扑等价性，Przulj把图元中具有相同拓扑位置的节点标记为相同的记号，然后对其中具有不同拓扑位置的节点唯一标号。图1 中包含了2-节点、3-节点、4-节点这三种图元的15 个不同的拓扑位置，称这些拓扑位置为自同构轨道，它们出现的频率记录为图元向量［16］。

由于在大规模生物网络中，非同构图元的网络结构差异各种各样，下面将会以一个简单无向网络为例来对自同构轨道的查找进行说明。

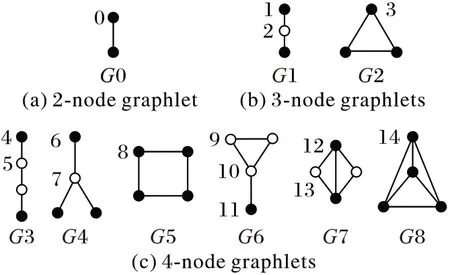
图1 图元及图元向量Fig.1 Graphlets and graphlet orbits

图2 展示了网络GA 所形成的无向网络图。在图2 中，以节点1 为例，发现一共有4 个0 轨道向量，即（1，2）、（1，3）、（1，4）、（1，5），那么节点1 的0 轨道向量的数目就是4；同样地，当以节点2 为例时，0 轨道向量的数目是4，即（2，1）、（2，3）、（2，4）、（2，5）。其他轨道向量数目的计算过程依此类推。

表1展示了图2实例中每个节点的轨道向量数目，其中行代表了轨道向量编号，3 个图元中轨道向量的总数目为14。列则代表了每个节点的编号。

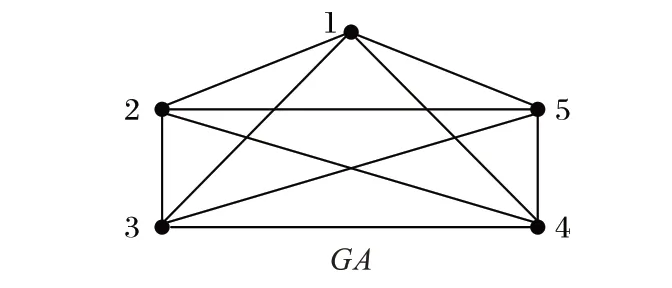
图2 无向生物网络实例Fig.2 Example of undirected biological network

表1 图2中5个节点在GA网络中图元向量的数量Tab.1 Number of graphlet orbits of the five nodes in the GA network of Fig.2

2 GDV方法的实现

GDV 方法是一种在连通生物网络中枚举各节点自同构轨道数量的方法，可以大致分为网络初始化、自同构轨道查找和统计自同构轨道数量三个步骤。其中网络的初始化是该方法的准备工作，需要将边集形式转换为一个无向生物网络，之后再将网络转换成一个n×n（n 指的是无向网络的节点数目）的邻接矩阵用以存储每个节点以及节点所对应的边；GDV 方法所提出的自同构轨道查找保证了所枚举图元的唯一性和查找自同构轨道数量的准确性；最后是统计每个节点所对应的自同构轨道的数目，将其存储在一个n×15 的矩阵中。查找每个节点的自同构轨道是整个GDV 方法的核心部分，因此，下文在介绍GDV 方法的前提下，将着重介绍每个节点自同构轨道的查找过程。

GDV方法的具体实现步骤（主要步骤如图3）如下所示：

步骤1 网络的初始化。GDV 方法在构建网络时输入为边集的形式，节点的编号以连续的数值表示，边由节点对来确定是否进行生成，若两个点的节点值在同一个节点对中，那么就生成连接这两个节点的边。如图2 就是由GA 的边集所构建的无向网络。然后将生成的网络转换成一个n×n 的邻接矩阵，其中n 表示网络的节点数。例如将图2 的GA 无向图转化为邻接矩阵A：

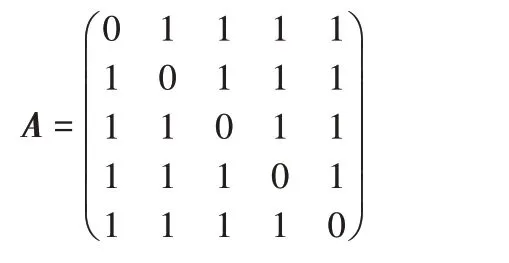
步骤2 查找每个节点的图元向量的数量。对每个节点进行遍历，查找其与相邻节点之间的关系，进而来判定属于哪一种自同构轨道。通过分析可以得到，在图1中，G0图元可以通过一个二维循环来对0 轨道进行查找，从而计算2-节点图元中0 轨道的数量，但是当计算3-节点或者4-节点的图元向量时，二维循环难以解决复杂的计算过程。本文采用了Xie等［5］于2017 年实现的基于2-4 nodes 的方法，该方法对不同的图元向量进行了分类枚举，巧妙地避开了在二维循环中计算过程复杂的问题，同时也确保了整个查找过程的严谨性，做到了精确查找。在该方法中对3-节点的图元向量进行了三维循环操作，针对4-节点的图元进行了四维循环操作，有效地解决了复杂的查找过程，但该方法的时间复杂度非常高。

步骤3 将步骤2 查找的结果存储到一个n×15 的矩阵中，用以记录每个节点的图元向量的数量。

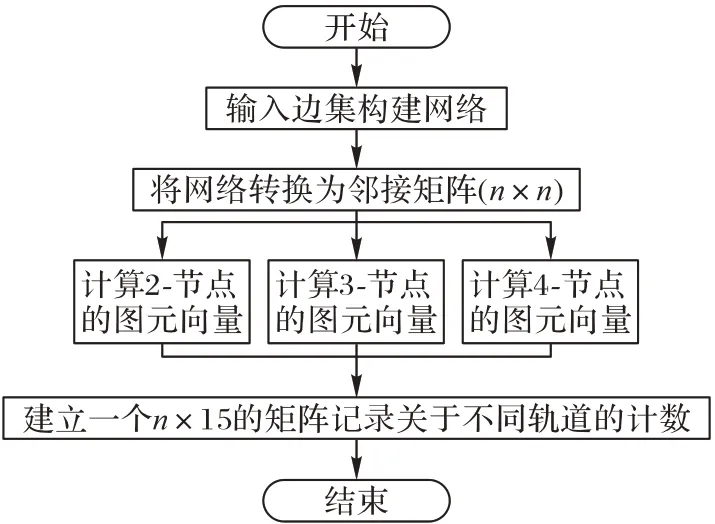
图3 GDV方法的主要步骤Fig.3 Main steps of GDV method

3 GDV方法的优化及其并行化的实现

枚举每个节点的非同构轨道数量的操作是整个GDV 方法的核心部分，同时也是整个方法中最耗时的部分，因此本文从查找每个节点的非同构轨道数量这一步骤上进行突破，完成了两方面的工作：1）将串行GDV 方法实现并行化。2）分为两步对GDV方法进行了优化：①改进GDV串行方法解决邻接矩阵中重复计算的问题，同时进行并行化；②将改进后的并行化GDV 方法进行优化以解决各进程的负载不均衡问题，实现负载均衡。

3.1 GDV串行方法的并行实现

GDV 方法的主要任务就是寻找一个网络中每个节点的自同构轨道的数量，由GDV方法步骤2的分析可知，在寻找每个节点的自同构轨道时，根据图元向量的不同类别进行不同层次的循环查找就可以计算出不同节点的自同构轨道，所以可以将这类问题转化为矩阵的运算来进行，针对矩阵的运算，本文实现的是按照行数来进行进程间任务的分配，最后再将子任务的结果规约至0号进程。

3.2 GDV串行方法的重复计算问题改善及其并行化实现

尽管进行了GDV 方法的并行化实现，但是该并行方法仍然耗时甚多，为了尽可能地提高该方法的运行效率，首先对GDV 串行方法进行了解决重复计算问题的改进，然后将改进后的方法实现了并行化。

自同构轨道数量的计算中，需要针对无向网络中每个节点进行遍历，查找该节点与邻居节点的关系，进而确定以该节点为目标节点的自同构轨道的数量，查找的过程是在无向网络转换为邻接矩阵后进行的。众所周知，无向网络转换为邻接矩阵后往往表现为是一个上（下）三角矩阵，以网络GA 为例，很显然它的邻接矩阵A是一个上（下）三角矩阵，因此在计算的过程中只需要针对上（下）三角矩阵进行查找即可，然后再根据对称关系，在相应的自同构轨道上记录，最后得到结果。该过程的伪代码如下所示：

伪代码中，在进行第二次循环遍历时，仅需要从第一个位置的下一个元素进行遍历即可，不需要再从头进行遍历，这样大大地缩短了对比所需要的时间；不过，在遍历的同时，还需要对邻接矩阵其对应位置的自同构轨道的数量进行记录，这样才能在记录时避免出现遗漏的现象。由前面的讨论可知，GDV 方法最耗时的部分是对每个节点进行枚举自同构轨道的数量，因此进行并行化处理时需要针对这一问题展开分析，将矩阵按照进程数来进行行分，用以实现并行化。

3.3 改进后GDV方法的并行优化

传统的矩阵行分较为规则化，但是在本文中由于改进后的GDV 方法中提供的是一个上（下）三角矩阵，使用传统的方法进行行分时，就会出现每个进程负载极其不均衡的情况，因此在对矩阵进行行分时，需要改进策略，以解决负载不均衡的情况。改进策略属于一个动态规划的问题，程序需要根据进程数来进行合理行分。本文所采取的策略如下：

步骤1 根据矩阵的行数和进程的规模数进行划分，具体划分规则为：size*=n/(numprocs*2)。

步骤2 将得到的size*按照进程编号的顺序分发给各个进程，此时所有进程运算的矩阵的行数为总体行数的一半。

步骤3 将得到的size*按照进程编号的逆序再次分发给各个进程，此时所有进程运算的矩阵的行数为总体行数的另外一半。

步骤4 根据主进程分发的规模，各进程开始进行计算。

步骤5 各进程将所得到的计算结果归约求和发送给主进程，并行结束。

4 实验与结果分析

4.1 实验环境

本次研究使用的实验平台是上海大学高性能计算集群“自强4000”。实验使用4 个内存节点，每个内存节点配置信息如下：2 颗Intel E5-2690 CPU（2.9 GHz/8-core），内存大小为64 GB。集群节点间使用标准的CLOS 二层Infiniband 网络架构，MPI 库版本为IntelMPI，实验运行操作系统为CentOS 6.3，编程语言为C++。

4.2 实验数据

实验同时使用了模拟数据和真实生物网络数据进行性能分析，其中模拟数据使用NetworkX［17］的python 包模拟了三类不同的网络模型，分别是无标度网络模型［18］、小世界网络模型［19］和规则网络模型［20］。

为了分析改进后的GDV 方法在不同网络模型中的可拓展性以及泛化能力，实验中使用了边数相同（均为4 000）但节点数不同五种网络模型进行实验，具体情况如表2所示。

表2 五个模拟网络数据集Tab.2 Five simulated network datasets

为了分析网络的边数对改进后方法的影响，真实生物网络选取了酵母菌代谢网络（Yeast Protein Interaction Network，YPIN）和人类基因调控网络（Human Genetic Regulatory Network，HGRN）两个生物网络数据集，其中HGRN 数据来源于STRING（Search Tool for Recurring Instances of Neighbouring Genes）在线数据库［21］，YPIN数据集来源于Uri Alon实验室［22］。这两个网络的特点是节点数大致相同，但边数不同：YPIN 的节点数为689，边数为1 078；HGRN 的节点数为709，边数为5 560。

图4（a）为并行的GDV方法在5种网络中所使用的时间比对。比较小世界模型、随机模型和无标度模型，三种模型的节点数均为1 000，边数为4 000，在图4（a）中可以看出这三种网络在相同核数下所花费的时间相差不大，因此可以认为在并行的GDV 方法中自同构轨道的查找与网络的种类是不相关的。通过观察图4（a）可以看出，尽管两种真实网络的边数相差很多，但它们的程序运行时间却相差不多，因此可以认为并行的GDV方法与网络的边数并不相关。

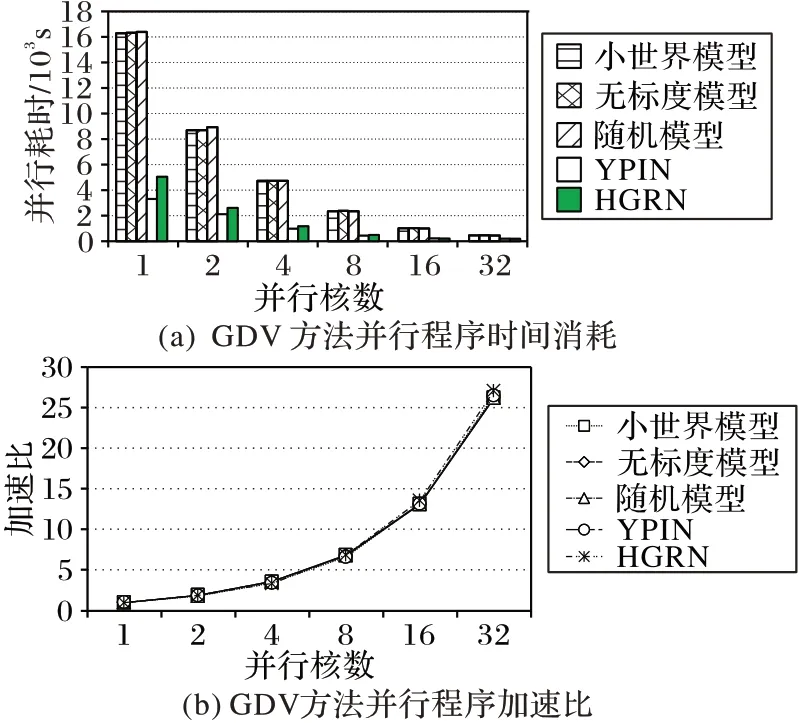
图4 GDV方法的并行性能Fig.4 Parallel performance of GDV method

图4 （b）是并行的GDV 方法在5 种网络中的加速比对比曲线。这5 种网络虽然规模不相同，但它们的加速比曲线几乎重合，加速比数值几乎相同，说明了并行的GDV 方法应用范围广，在不同的模型中均有好的作用。

在GDV 方法中，查找自同构轨道的计算开销比较大［12］，而且随着网络节点规模的增大，其运行时间消耗得也越来越多，以表3 的两种生物网络和表2 中编号3、4、5 的1 000 个节点的网络为例。从实验结果图4（a）中可以看出，当单核运行程序查找自同构轨道数量时，YPIN 和HGRN 网络查找时间将近1 h，而表2的1 000节点的网络的运行时间长达近4 h，两类网络节点之差仅300 个节点左右。由分析可知，整个查找自同构轨道的运算过程时间复杂度达到了O（n4），因此其运行时间也会随着网络规模的增大，呈现出幂函数4 次方级别的增大，因此对于GDV方法的并行化计算是十分有必要的。

4.2.1 解决重复计算问题后的结果

为了验证解决重复计算后GDV 方法的有效性，在表2 中编号3、4、5 的网络和YPIN、HGRN 两个真实网络下进行多次测试，各种条件下的测试结果都很相似，因此，选取了生成网络中的一个测试结果进行描述，生成网络中选取的是编号为3 的无标度网络，结果如图5 所示。从图5 可以明显地看到，在同一个网络中，在不同的核数并行情况下，改进后所消耗的时间远比改进前所消耗的时间少，这在其他的网络中也有所体现。

图5 无标度网络在解决重复计算前后的时间消耗Fig.5 Time consumption before and after solving double counting in scale-free network

但是，解决了重复计算的问题后还面临着各进程资源分配极其不均匀的问题。为了验证资源分配不均匀这一问题，选取了表2 中编号3、4、5 的网络以及YPIN、HGRN 两个真实网络模型作为数据集，它们在不同并行核数下程序时间消耗以及加速比如图6所示。

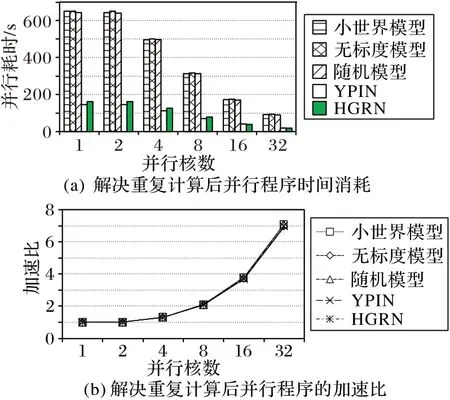
图6 解决重复计算后的并行性能Fig.6 Parallel performance after solving double counting

由图6（a）可以看出，5 个网络模型在使用一个核和两个核进行运算时，所消耗的时间相差无几，而且由图6（b）可以看出，该并行性能的加速比比较低，原因就是进程之间的资源分配不均匀。因为在多进程的情况下，某一进程所分得到的资源要远比其他兄弟进程多，从而导致在计算时，该进程所花费的时间远远多于兄弟进程，所以造成了这种加速比极低的情况。

从稳定性方面进行分析，通过观察图6（b），可以得出五个网络模型加速比一致，其稳定性良好。

4.2.2 采取负载均衡策略的实验结果

本节实验对4.2.1 节提到的各个进程之间资源分配不均衡做出了改进，通过对表2 中编号3、4、5 的网络和YPIN、HGRN 两个真实网络进行了多次测试，与采取负载均衡策略前的结果进行了对比。实验在5个网络中分别进行了10次测试，选取了计算所需时间的平均值，并计算出改进前后的加速比，对比结果如图7所示。

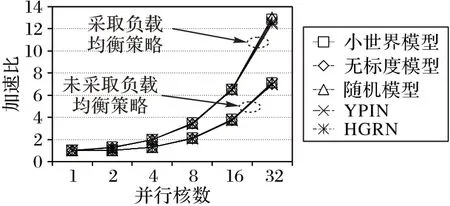
图7 采取负载均衡策略后的实验对比Fig.7 Experimental comparison after adopting load balancing strategy

图7 展示了采取负载均衡策略后加速比的提升，上面的5条曲线展示的是前文提及的5 个网络模型采取负载均衡策略后的加速比，而下面5条曲线则表示的是5个网络模型未采取负载均衡策略的加速比，可以看出加速比提升较高，并且随着并行核数的增大，加速比的提升空间也越来越大。

4.2.3 GDV方法改进后的并行性能

本节主要研究对GDV 方法进行了两步优化策略后的并行性能。为了说明改进后的GDV 方法与网络的节点和边的关系以及该方法是否有良好的拓展性，本次实验选取了表2中编号1、2、3 的网络进行测试，该网络选取的是随机生成的无标度网络，结果如图8所示。

图8 无标度网络的并行性能Fig.8 Parallel performance of scale-free networks

在图8 所显示的实验结果中，选取的网络为无标度网络，三个网络的节点分别为500、800、1 000，其对应的网络的边数都为4 000。从图8（a）来看：随着核数的增加，运行时间变得越来越少，有较好的并行结果；在节点数与核数一定的情况下，从所耗时间角度来看，节点数越多，耗时越久。从图8（b）来看：随着核数的增加，加速比也在上升，但是加速比增加的效果并不是很理想，随着核数的增加，加速比呈现出了非线性上升的状态；纵向来看，尽管节点数不相同，但是它们的加速比曲线相互叠加，因此可以看出改进后的GDV 方法拥有良好的扩展性。

5 结语

本文实现了GDV 方法的并行计算，同时还提出了一种改进策略应用于GDV 方法：针对原有串行算法在计算自同构轨道时耗时较长的问题，提出了解决重复计算策略和负载均衡策略，大大地节省了程序运行时间并且实现了并行计算的负载均衡。本文使用了多种模拟网络数据和真实生物网络数据进行测试，测试结果表明，GDV 的并行方法及改进后的GDV并行方法在多个数据集上都能得到较好的加速比，有效解决了自同构轨道查找效率低的问题。